基于改进粒子群优化算法的钢框架抗震优化设计

， ，

(浙江工业大学 建筑工程学院，浙江 杭州 310014)

粒子群优化算法(Particle swarm optimization，PSO)是由学者Kennedy 和Eberhart受鸟群觅食行为启发而提出的一种全局优化算法，其主要思想是通过个体之间的合作和信息共享实现对目标问题的求解[1]。相较其他演化算法，粒子群算法具有容易实现、需要调整的参数少、鲁棒性强以及只需较小的演化群体等优点，自提出就受到了研究者的广泛关注。李峰等[2]将PSO算法应用于桁架优化设计；林建荣[3]使PSO算法应用于钢桁架拱桥设计；蔡宝佩[4]运用PSO算法对刚架结构进行了优化设计。在结构工程中，将PSO算法应用于不同结构体系的优化设计研究相对较多，但这些研究中，将PSO算法应用于实际结构系统抗震优化设计的研究较少。

为将PSO算法应用于结构抗震优化设计中，选取钢框架为优化设计结构体系，以结构顶层位移和层间位移角作为性能指标，构建抗震优化模型；采用Push-over抗震分析方法对构建好的模型进行抗震分析。此外，为了使PSO算法更好地对抗震模型进行优化设计，引入相关学者观点，对PSO算法进行改进：1) 引入一种动态惯性权重，平衡好算法开发能力和探索能力；2) 粒子速度更新时，在全局邻域搜索加入一定的邻域空间，增加粒子寻优范围；3) 粒子位置更新时，将每次迭代得到的连续解映射到对应的定值离散区间中，进而得到符合要求的离散解。最后，通过一榀三层四跨钢框架典型算例的求解并与相关文献的结果进行对比，以评价利用改进后PSO算法进行钢框架抗震优化设计的效果。

1 抗震优化模型

基于性能的抗震设计思想是建筑结构抗震设计的一个重要发展阶段，基于性能的抗震设计思想使得设计的结构在地震作用下能够维持所要求的性能水平，结构的性能目标如应力水平、荷载、位移、极限状态和目标损伤指标不被超越。Push-over分析方法是目前评估结构抗震性能的重要方法之一，该方法本质上是一种与反应谱相结合的静力弹塑性分析方法，具有易于发现结构的薄弱部位、较直观地判断结构的抗震能力等优点。笔者依据美国抗震设计规范FEMA-273[5]和FEMA-350[6]中相关规定，并以结构顶层位移和层间位移角为性能指标，采用Push-over抗震分析方法进行钢框架结构抗震优化设计。

1.1 目标函数

钢框架设计中，结构的重量越轻，消耗的材料就越少，一般工程造价就越低。同时，钢框架重量降低还可减少基础的承重，改善基础的受力情况。因此，在不考虑钢框架梁、柱节点连接处质量的前提下，以钢框架结构材料总质量最小为优化目标，建立目标函数为

(1)

式中：ρi，Ai，Li分别为钢构件i的密度、截面积和长度。

1.2 设计变量

参照美国钢结构型钢表中的274 种H型钢，验证算例中的钢框架抗震优化模型的钢构件设计变量(包括截面积、截面惯性矩、截面抵抗矩和截面塑性抵抗矩等)均选定于这274 种H型钢。

1.3 约束

工程实践表明：由地震作用引起的建筑物轻微侧向位移可能导致人在心理上的不适和建筑的非结构性损害，而强地震引起的过大非弹性变形往往有可能使建筑内以及建筑周边的机械、电气和管道系统等出现故障，或吊顶和设备坠落，从而对人的生命造成威胁，这种过大的建筑侧向位移会增加建筑的不稳定性，从而降低结构安全[7]。因此，在抗震设计过程中，必须有意识地控制建筑侧向位移在规范规定的范围之内。

FEMA-273[5]将结构抗震性能水平分为正常使用(Operational)、立即入住(Immediate occupancy)、生命安全(Life safety)和防止倒塌(Collapse prevention) 4 种等级，并规定建筑物在这4 种等级水平状态下最大侧向位移分别取建筑结构高度的0.4%，0.7%，2.5%，5%，且在第一等级(正常使用)性能状态之前，结构各节点不允许出现塑性变形。此外，FEMA-350[6]规定了第2和第4性能水平状态下建筑层间位移角的限值分别为1.25%和6.1%。具体4 种性能水平状态下约束条件为

OP等级：ΔOP≤0.4%H

(2)

IO等级：ΔIO≤0.7%H,θIO≤1.25

(3)

LS等级：ΔLS≤2.5%H

(4)

CP等级：ΔCP≤5%H,θCP≤6.1

(5)

式中：ΔOP，ΔIO，ΔLS，ΔCP分别为结构在4 种性能状态下的顶层侧向位移；θIO，θCP分别为结构在第2和第4性能状态下层间位移角。

1.4 约束处理

钢框架抗震优化模型中，最终的目的是得到在满足约束条件情况下各钢构件最优截面类型。结合粒子群算法的特点，需要使目标函数值(各钢构件质量)在粒子进化迭代过程中不断降低，从而筛选出靠前的较优解，但这样一来往往在迭代过程中一些目前虽不是最好但有潜力成为最好的解，由于稍微违反约束条件而过早被遗弃的问题，从而使得整个粒子群失去了这些有潜力解的引导，进而陷入局部最优。为了克服以上问题，选用一种罚函数处理机制[8]，该方法通过适当的λ1和λ2取值达到对那些稍微违法约束条件的解给予适当的惩罚却又不至于完全“一棒打死”的效果，使得这些解仍有机会在后续的迭代过程中走向最优或较优。该方法的罚函数设置为

F=W×(1+λ1V)λ2

(6)

式中：F为罚函数值；λ1，λ2为惩罚因子；V为结构的总体约束违反程度，其表达式为

V=VOP+VIO+VLS+VCP+θIO+θCP

(7)

(8)

式中：Vj(j=OP，IO，LS，CP)，θk(k=IO，CP)分别为各性能状态下结构对顶层位移和层间位移角的违反程度；pi为结构i节点塑性程度。

1.5 Push-over计算分析方法

Push-over计算分析的思路是借用弹性体系的振型分解反应谱的概念，将结构各振型下的水平地震力作为静力荷载施加到结构上，进而逐步将结构推至一个给定的目标位移来研究分析结构的非线性性能，从而判断结构及构件的变形受力是否满足设计要求。在Push-over分析方法中选择合理的加载模式是一个关键问题，典型的加载模式有均匀加载、倒三角加载、指数加载和多振型加载等模式，如图1所示。当抗震优化结构模型规则且高度较小时，可以忽略高振型的影响，只需考虑第一振型的作用[9]。由于验证算例是三层四跨钢框架结构，故此可以选定一种水平加载模式进行Push-over分析。为了与相比较的文献相统一，采用指数加载模型，其施加的水平荷载[10]计算式为

(9)

式中：Px为第x层水平荷载；Wx，Wi分别为x，i层重力荷载代表值；hx，hi分别为x，i层距地面的高度；n为结构总层数；k为与结构基本周期有关的参数，这里k=2；Vb为结构底部剪力。

图1 水平加载模式示意图Fig.1 Horizontal loading schematic diagram

2 粒子群优化算法改进

2.1 惯性权重

Shi和Eberhart最早提出了惯性权重ω的概念，通过合适惯性权重ω可很好地控制粒子的搜索范围，让粒子保持着运动的惯性，使其搜索空间得到扩展，从而有机会在新的区域内探寻最优解。为使PSO算法更好地应用于结构优化设计，引入一种动态惯性权重为

(10)

式中：ωmax，ωmin为惯性权重上、下限；itermax为最大迭代次数；iter为粒子当前迭代次数；k，u为试验常数。如图2所示，该方法通过综合控制公式中的k，u取值。图2给出了3 种情形：k=5，u=10；k=10，u=10；k=10，u=5。可以使得粒子群在前期获得较大惯性权重以利于拓宽粒子搜索空间，中期惯性权重取值下降较快，提高算法搜索效率，后期取较小惯性权重以利于粒子在最优解附近进行精细开发。

图2 动态惯性权重Fig.2 Dynamic inertia weight

2.2 速度更新

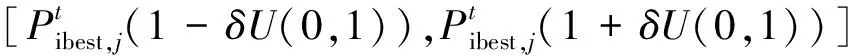
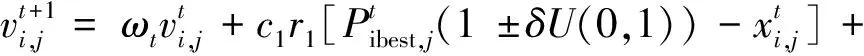
(11)

(12)

式中：t为粒子进化代数；c1，c2为认知因子和社会学习因子；r1，r2，U(0,1)均为区间(0,1)上的均匀分布随机数；δ为扰动因子；Pibest为个体最优；Pgbest为全局最优。

2.3 取值离散化

标准粒子群算法对连续问题具有较高的适用性，而对于离散问题，往往需要对标准粒子群算法加以修正。钢框架优化模型中的设计变量为美国钢结构型钢表中的274 种H型钢，因此采用标准粒子群算法需要对粒子群每次迭代得到的连续解加以处理，使其与274 种H型钢对应。改进PSO算法引入一种将迭代过程中寻优得到的解映射到定值离散区间中的方法[4]，该方法仍采用式(11，12)中求解连续问题的速度和位置迭代公式，将粒子每次迭代结束后得到的位置向量同274 种H型钢截面积进行比较，将位置向量中的每一个元素取为最接近的型钢截面积。

基于改进粒子群优化算法的钢框架优化设计流程如图3所示。

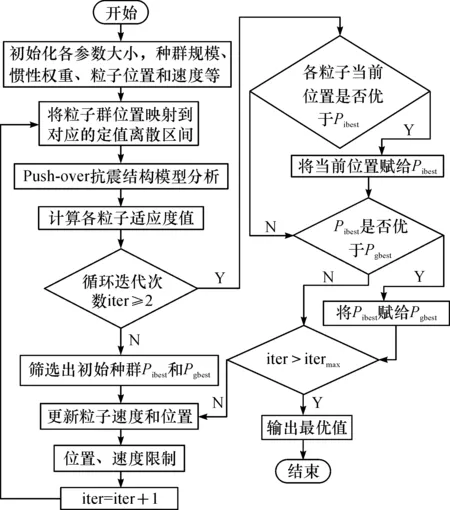
图3 基于改进粒子群算法的钢框架抗震优化设计流程图Fig.3 Optimization design flow chart of steel frame based on improved particle swarm optimization

3 优化算例

采用文献[7]中的一榀三层四跨钢框架抗震优化模型算例，结构如图4所示。模型中，钢框架各构件分为5个组别，同一组别钢构件采用同种型钢，钢材弹性模量为200 GPa，密度7 849 kg/m3。框架梁、柱的屈服强度分别为339，397 MPa。恒、活荷载组合、分配后，对结构第一、二层施加32 kN/m的线荷载，对顶层施加28.7 kN/m的线荷载。另外，第一、二层的地震设计重量分别均为4 688 kN，顶层地震设计重量为5 071 kN。

图4 三层四跨钢框架Fig.4 The four-bay three-story fram

在该算例中，改进PSO算法各项参数设置为λ1=0.9，λ2=2，ωmax=0.9，ωmin=0.4，itermax=200，k=10，u=5，c1=c2=2，δ=0.01。编制改进PSO算法Matlab主程序，以钢框架顶层位移和层间位移角作为性能指标，采用Push-over程序对结构作抗震分析，对钢框架算例作基于性能的结构抗震优化设计。

在相同的约束条件下，随机对算例作10 次优化测试，图5给出10 次优化测试得出的具体结果，表1取最好结果与最差结果，并与其他文献结果进行对比。

图5 改进PSO算法10 次优化测试结果Fig.5 Result of the optimization using the improved PSO in 10 times

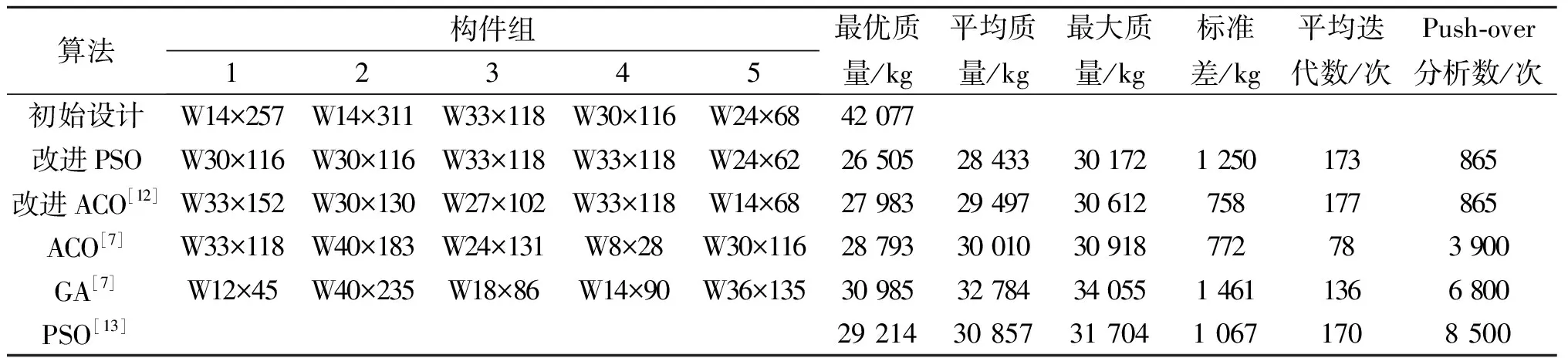
表1 优化结果与初始设计对比Table 1 Comparison of the optimization and the initial design

由表1和图5中优化结果中的钢材用量可以看出：改进PSO算法相比于文献[13]的PSO算法在求解质量上提升显著。改进PSO算法随机优化10 次得到的钢材最优质量为26 505 kg，仅为初始设计用钢量的62.99%，相比于改进ACO[12]，ACO[7]，PSO[13]，GA[7]算法得到的优化结果，分别节省了1 478，2 288，2 709，4 480 kg钢材。从10 次试验优化得到的平均用钢量和最大用钢量看，改进PSO算法同样表现出了巨大的优势，改进PSO算法得到的平均用钢量为28 433 kg，低于相比较的几种优化算法得到的平均用钢量，且10 次得到的平均用钢量已低于PSO，ACO，GA这3 种优化算法得到的最优质量。

图6给出了改进PSO算法与几种相比较算法的平均迭代次数和Push-over分析次数的对比情况。改进PSO算法的平均迭代次数为173 次，相比PSO算法，GA算法，ACO算法分别多了3，37，95 次迭代，比改进ACO算法少了3 次迭代。单就比较平均迭代次数这一数据，改进PSO算法与PSO，ACO，GA这3 种算法相比似乎没有优势，造成这样的原因是这3 种算法优化程序中选用的优化个体数m= 50，因而算法每轮迭代需作50 次Push-over分析。选取多的优化个体数，增加了种群丰富度，有利于优化个体遍历解空间。而改进算法在粒子速度更新时，在全局邻域搜索加入一定的邻域空间，增加了粒子寻优范围；通过适当的罚函数机制，增加了粒子在迭代过程中一些有潜力解对整个种群的引导，因此改进算法中粒子数不需要设置那么多，将验证算例中的粒子数选取为5 个。通过对优化程序进行200 次迭代试验发现：整个优化程序需用时大约1 351.88 s，其中改进的PSO主程序和调用的Push-over程序运行时间分别为4.32，1 347.56 s，调用的Push-over程序运行时间占总程序运行时间的99.68%。选取过多的优化个体数意味着过高的Push-over分析次数，进而导致整个优化程序运行时间增加。在忽略不计主程序运行时间的情况下，改进PSO算法的平均搜索求解时间仅为文献[7]中ACO算法的13.72%，文献[12]中改进ACO算法的60.48%，由此可见改进PSO算法在寻优求解速度和效率上提升显著。

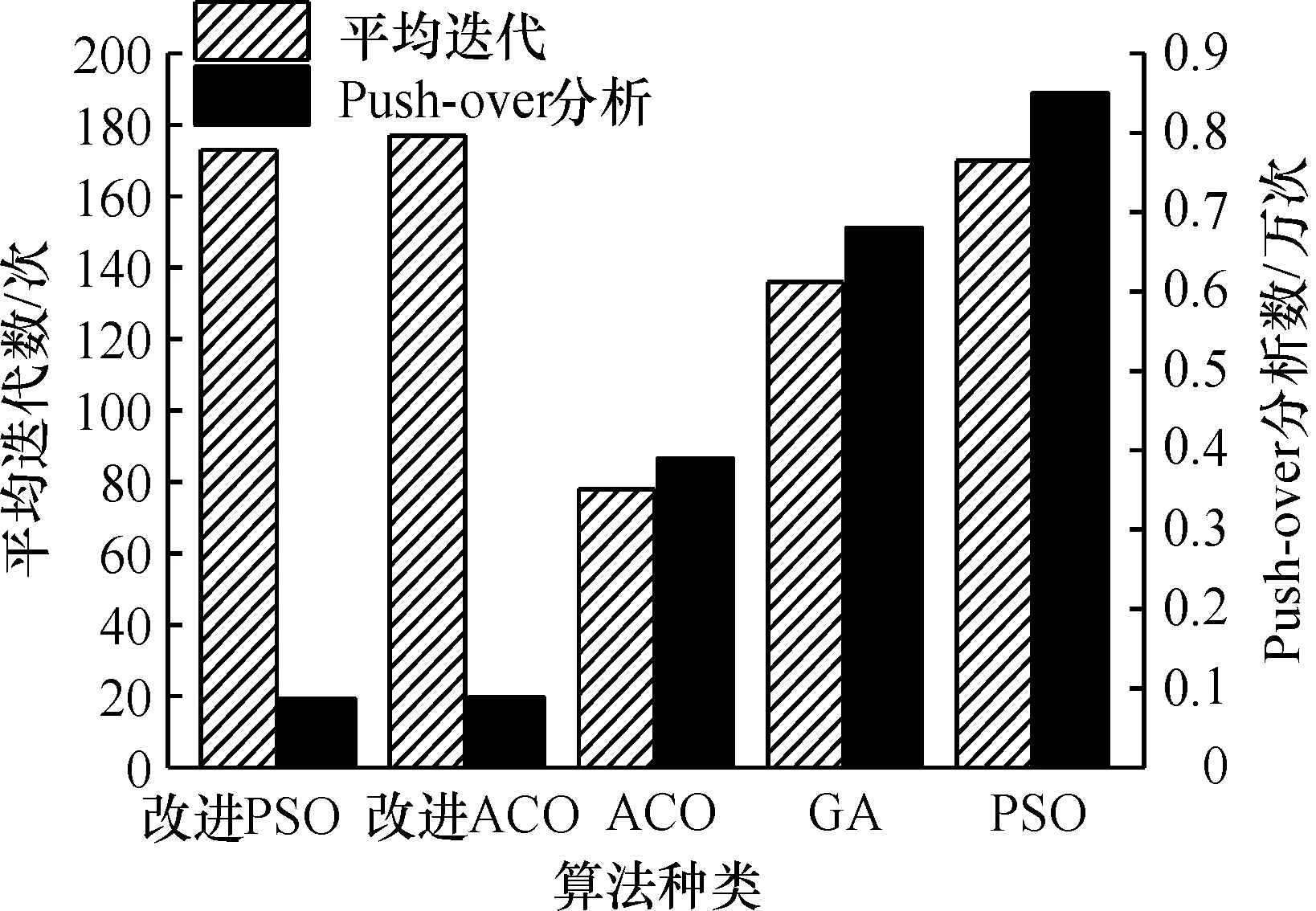
图6 平均迭代次数与Push-over分析次数对比Fig.6 Comparision of the average iterations and the number of Push-over analysis

图7给出了改进PSO算法在求解到最优解时的迭代过程曲线，由此可以看出改进PSO算法在迭代前期能够迅速收敛到最优解附近，从而在最优解周围进行精确搜索。表2给出了改进PSO算法与相比较的几种算法在不同抗震性能水平下的顶层位移和层间位移角指标。最优解下结构的各层水平位移和位移角均在规范规定的范围之内，且与几种相比较的算法相比，改进的PSO算法应用于三层四跨钢框架优化设计得到的结构各层水平位移和位移角更小。由此可以得出改进算法在应用于三层四跨抗震优化模型中不仅可以大量的节省设计材料，而且设计出来的钢框架结构抗震性能更优。

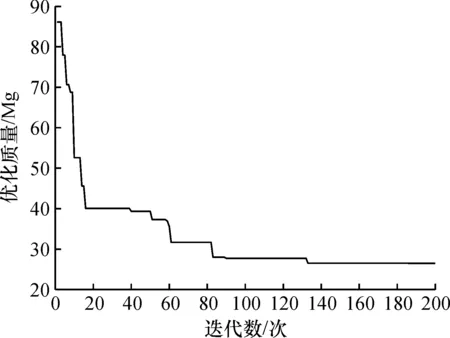
图7 优化迭代曲线Fig.7 Optimization iteration curve

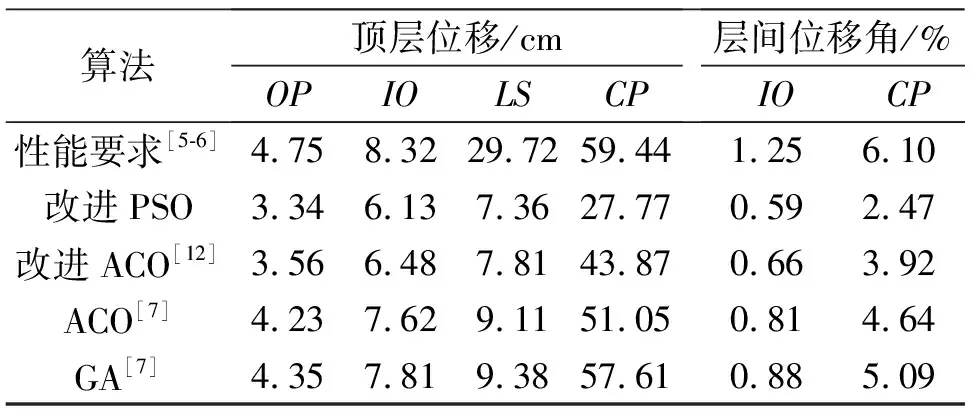
表2 最优解下结构抗震性能水平

图8给出了最优解下结构的等效地震荷载—顶层位移的Push-over曲线，图9给出了框架各构件在4种等级的性能目标水平状态下的塑性发展状况。OP性能状态之前，框架各构件均处于弹性阶段，荷载与顶层位移成线性关系，随着施加在结构上的等效地震荷载的增大，顶层框架梁结点处最先达到屈服强度，呈现出塑性变形，且顶层最左跨一梁结点率先出现塑性铰。IO状态后，底层柱开始出现塑性变形。随着施加在结构上的等效地震荷载进一步增大，顶层位移急剧增大，梁构件结点处均进入塑状态，中跨三根柱下节点处稍出现塑性，这种梁柱塑性发展过程正好暗合了结构设计中“ 强柱弱梁”理念。通过定量计算发现，LS到CP段的结构顶层位移增量达到了弹性阶段总位移的6 倍多。

图8 Push-over曲线Fig.8 Push-over curve

图9 各性能状态下塑性状态Fig.9 The state of shaping in each performance state

4 结 论

通过惯性权重取值、速度更新方式和位置更新方式等三方面对标准粒子群算法进行改进，提高了粒子群算法的稳定性、求解速度及求解质量； 合理的罚函数机制解决了粒子群算法在迭代过程中经常失去一些有潜力解对种群的引导问题；一榀三层四跨钢框架算例表明改进粒子群算法在结构抗震优化设计中的适用性和有效性，改进算法可应用于钢框架抗震优化设计。