以离散曲线为测地线的离散曲面构造

,

(浙江工业大学 理学院，浙江 杭州 310023)

曲面上测地线是曲面的内蕴几何量, 曲面上任意两点间的测地线段是该两点间的局部最短连线。由于这一性质, 测地线被广泛运用于各领域中。比如, 工业产品或动画人物的网格外形复蓋件设计, 路径剪裁, 服饰鞋帽设计, 纺织材料生产等。

测地线在微分几何领域和CAGD领域中有很多重要的研究成果。过去测地线的研究主要集中在测地线的特征及计算。最近几年一部分学者开始研究以给定曲线为曲面特征线的曲面反求, Wang等[1]给出了以给定曲线为公共测地线的曲面束构造算法, 为后面学者的研究奠定基础, 这一课题提出以来, 相继有国内外众多学者进行了相关研究; Zhao等[2-3]提出了以给定曲线为测地线的有理Bézier曲面构造和以给定曲线为曲率线的可展曲面构造; Paluszny[4]提出过测地线的三次多项式曲面的构造; Sanchez-Reyes等[5]提出了从给定测地线反向构造带约束多项式曲面; Sprynski等[6]给出了插值测地线的曲面构造算法; Farouki等[7-8]进一步研究了以给定Bézier曲线为测地线的Bézier曲面构造和给定三条首尾相连的测地线为边界线的三角形Coon曲面片的构造和光顺; 陈杰等[9]提出了过测地线的近似极小直纹曲面设计; Li等[10-11]给出了过公共曲率线的曲面束参数表达式算法以及以已知曲线为测地线的近似极小曲面设计; 杨火根等[12]基于插值边界测地线的充要条件，提出了插值非均匀B样条曲线为等参测地线的非均匀B样条优化曲面设计; 寿华好等[13]提出带法向约束下B样条曲线拟合的实编码GA算法。可应用于曲面构造的度量函数设计。最近Sáchez-Reyes[14]又给出了过测地线的极小曲面算法。以上研究都是基于给定曲线为连续情况, 离散情况的研究寥寥无几。2015年,张威等[15]给了以离散曲线为曲率线的拟可展离散曲面的构造。在离散几何模型中, 许多连续的几何变量的计算变得复杂不精确。因为离散形式丢失了原几何模型的信息。所以以离散曲线为特征线的离散曲面反求相对比较困难。高家全等[16]提出了一种基于GPU的高效并行l1最小化算法, 可用于提升算法执行效率。刘震等[17]利用耳切三角化技术，提出了针对三维模型孔洞的一种基曲面构建方法。笔者提出了一种以给定离散曲线为测地线的离散曲面反求算法, 这里的离散测地线与三角网格中定义的测地线并不等价, 采用连续情况的定义。并将度量函数设计成B样条曲线, 这样设计者可以通过控制几个点便能设计出满足自身需求的曲面。

1 预备知识

令U={u0,u1,…,um}是一个单调不减的实数序列，即ui≤ui-1,i=0,1,…,m-1, 其中,ui称为节点, 用Ni,p(u)表示第i个p次B 样条基函数, 其定义为

(1)

p次B 样条曲线定义为

(2)

式中：{Pi}为控制点；Ni,p(u)为定义在非周期且非均匀节点矢量, 如式(1)所示。B样条还具有端点插值性, 即C(0)=P0,C(1)=Pn。

对C(u)求导得

(3)

2 过给定测地线曲面的参数表达式

给定空间参数曲线为

C:r=R(s),0≤s≤1

(4)

式中s为弧长参数。假设曲线满足R′(s)×R″(s)≠0, 即曲线上每一点都存在单位切向量、单位法向量和单位从法向量, 分别记为T(s),N(s),B(s),构成R(s)的Frenet标架。空间中过给定曲线R(s)的曲面P(s,t), 可以定义为

P(s,t)=R(s)+(u(s,t),v(s,t),w(s,t))·
(T(s),N(s),B(s))T
0≤s≤1,0≤t≤1

(5)

式中：u(s,t),v(s,t),w(s,t)为至少C1的函数, 也称为度量函数,u(s,t),v(s,t),w(s,t)反映曲面上的点在t时刻分别沿T(s),N(s),B(s)方向的行进的长度。Wang等[1]得出了以R(s)为测地线的曲面束, 度量函数u(s,t),v(s,t),w(s,t)应满足的约束条件(曲面法向)为

φ1(s,t)T(s)+φ2(s,t)N(s)+φ3(s,t)B(s)

(6)

其中

(7)

对于曲线R(s)的法向为

假设t=t0时P(s,t)=R(s), 则有N(s)‖n(s,t0),0≤s≤1, 即

φ1(s,t0)=φ3(s,t0)≡0
φ2(s,t0)≠0,0≤s≤1,0≤t0≤1

(8)

可化简为

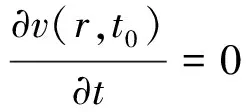
(9)

曲线R(s)给定, 以其为测地线的曲面就完全由度量函数决定, 只要度量函数满足式(9), 曲面的形状可自行控制。Zhao等[2]研究了这类曲面的构造, 当给定曲线R(s)为Bézier曲线时的曲面构造方法。

3 过给定测地线曲面的参数表达式

本节是笔者算法核心, 主要介绍如何设计满足约束条件式(9)的度量函数，为了使得u(s,t),v(s,t),w(s,t)设计简便, 不妨假设u(s,t),v(s,t),w(s,t)为可因数分解, 即

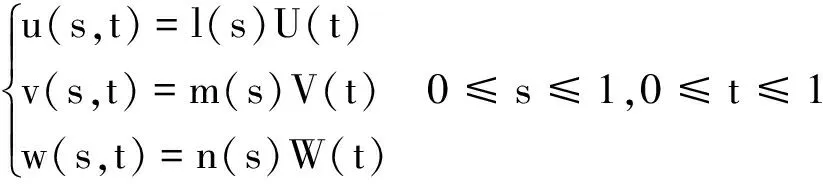
(10)

则式(9)可写为

(11)

其中假设

l(s)=m(s)=n(s)=1

(12)

3.1 度量函数为B样条函数

假设{U(t),V(t),W(t)}为R的Frenet标架下的一条B样条C(u), 这样便于设计者控制生成曲面的形状, 则式(11)可写为

(13)

由B样条的端点插值性和式(3), 则式(13)可表述为C(u)的控制顶点应满足P0=(0,0,0)(端点插值性),P0,y=P1,y,P0,z≠P1,z。

3.2 离散曲线的几何量计算

(14)

令r2,rn-1的密切圆作为端点r1,rn的密切圆, 即O1=O2,On-1=On。

(15)

3.3 离散曲面构造算法

以上两小节介绍度量函数和离散几何量的设计和计算, 将式(5)离散化为

(16)

构造曲面具体算法步骤如下:

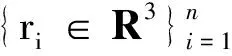
Step2根据自身需求分别设计满足式(13)中{U(t),V(t),W(t)}的B样条函数。

Step3根据式(16)计算离散曲面点。

4 实例

为了设计出符合自身需求的离散曲面, 以给定离散曲线为测地线，通过调整度量函数的节点向量U及其控制顶点{Pi}, 下面将展示以给定不同的离散曲线和度量函数, 分别构造不同的离散曲面。

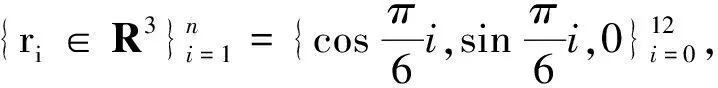
图1 度量函数相同Fig.1 Same march-function

例2在实际生产设计中, 可以为每个ri设计不同的度量函数来满足不同的需求。可以通过调整各个离散点对应的度量函数, 以修改曲面的局部形状。效果如图2所示。

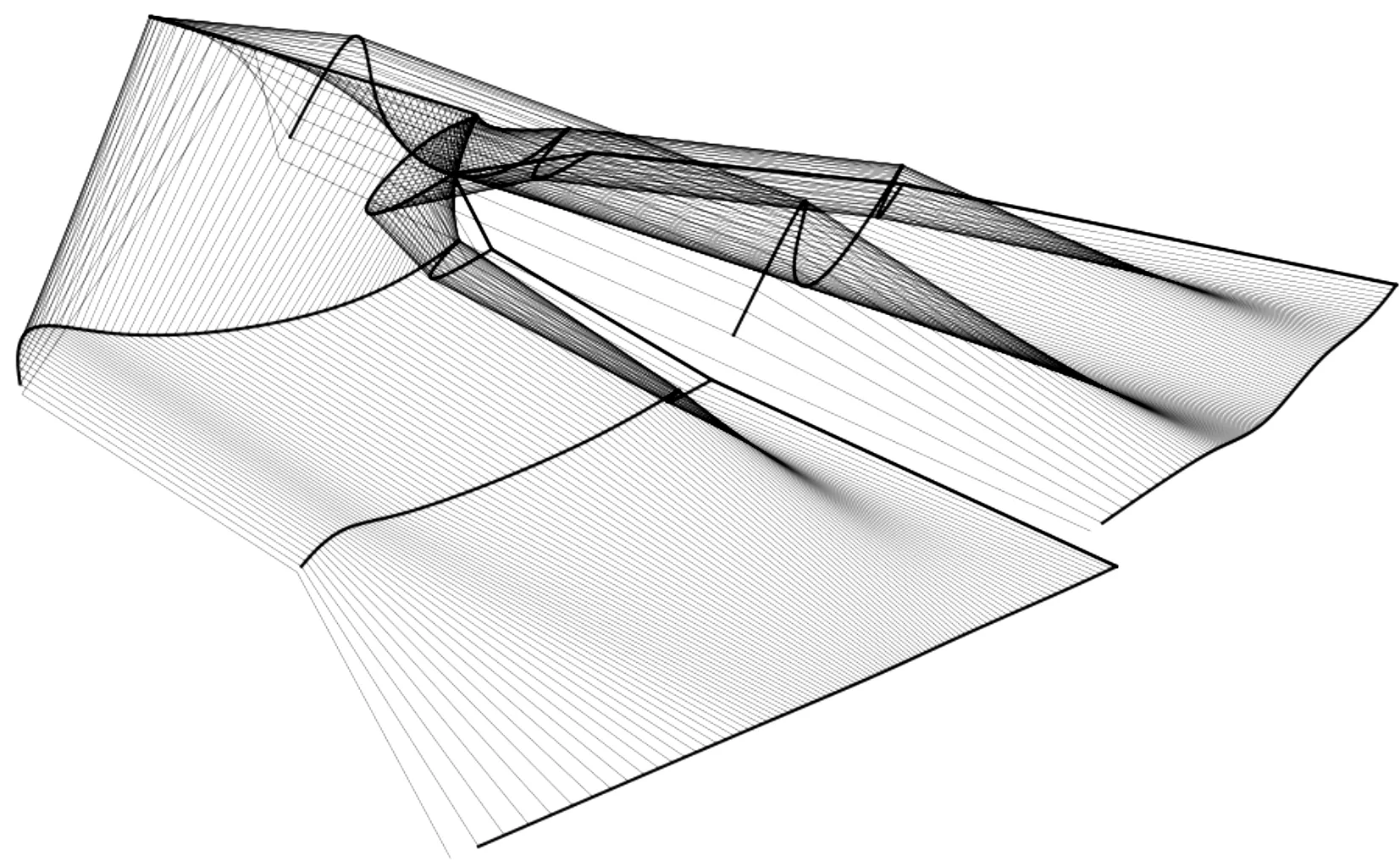
图2 度量函数不同Fig.2 Different march-function

5 结 论

以给定离散曲线为测地线的曲面构造这一课题,很多学者是将给定的离散曲线通过插值成连续曲线处理,最后在连续情况下进行曲面构造。笔者采用离散情况的曲面构造算法,让设计者通过控制度量函数来设计满足自身需求的曲面,如果普通的样条不能满足设计者需求,可以将度量函数设计为有理B样条。实验结果显示该算法在给定任意离散曲面的情况下,能够很好地控制和设计出满足自身需求的曲面,并且具有很好的交互性。笔者算法通过度量函数的构造来生成曲面,对不熟悉B样条的设计者来说可能在曲面的构造上需要多次调整和选择合适的B样条作为度量函数。今后的工作是研究如何在给定离散测地线的情况下直接生成离散曲面,或者是额外给定一些参数时，能够直接生成离散曲面,而不是通过度量函数控制曲面形状。