轮迹横向分布对异形钢桥面板疲劳性能的影响

，，

(浙江工业大学 建筑工程学院，浙江 杭州 310023)

伴随着JTG D64—2015《公路钢结构桥梁设计规范》的颁布与实施，推进公路钢结构桥梁的建设已经成为行业共识。随着经济快速发展，交通量日益增大，重载车辆日益增多，且超载现象层出不穷，公路钢结构桥梁的疲劳问题日益突出[1-2]。研究表明：桥面板构造细节处的应力幅对车轮位置较为敏感[3-4]，因此钢结构桥梁的设计应考虑车轮荷载的作用位置。由于车辆在行驶过程中，轮迹在桥面的分布有很大的随机性，欧洲规范[5]及英国规范[6]等均基于实测值给出了轮迹横向概率分布模型，国内也在新颁布的JTG D64—2015《公路钢结构桥梁设计规范》里参照欧洲规范对这一因素予以考虑。

不论国内国外，在给出的轮迹在车道上的横向概率分布图中并未对车辆直线行驶和车辆转弯时两种不同情况加以区分。轮迹分布情况与行车时的路面状况及驾驶人的心理因素有较大关系[7]，考虑到驾驶人驾驶汽车在直线行驶和转弯时不同的心理状况，有必要对车辆荷载在转弯时的轮迹横向分布加以研究。笔者对温岭市某处交通量较大的路口处右转弯车辆的轮迹进行实测并统计分析，得到车辆右转弯时的轮迹横向分布图，并以温岭市某座异形钢箱梁为背景工程，建立ANSYS有限元模型，分析车辆轮迹横向分布对异性钢箱梁桥面板几处典型构造细节应力幅的影响。

1 轮迹横向分布统计

浙江省温岭市曙光支路桥空中对接曙光西路2号桥工程，其连接段为异形钢箱梁结构，主要受力结构由钢箱加劲梁和钢横梁组成。梁高 700 mm，曙光西路2号桥人行道钢箱梁腹板厚 30 mm，支路段腹板厚 20 mm，横梁厚 20 mm，桥面系顶板采用带U肋的正交异性板结构，顶板厚20 mm。异形钢箱梁平面图及横断面图如图1，2所示；U肋厚8 mm，其构造细节及过横梁处开孔构造细节如图3所示。

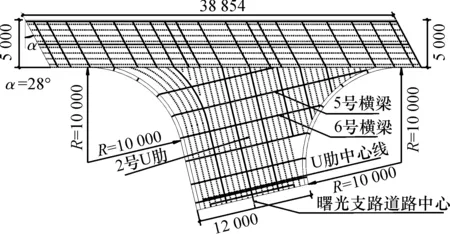
图1 异形钢箱梁平面图Fig.1 Plan of the special-shaped box girder bridge

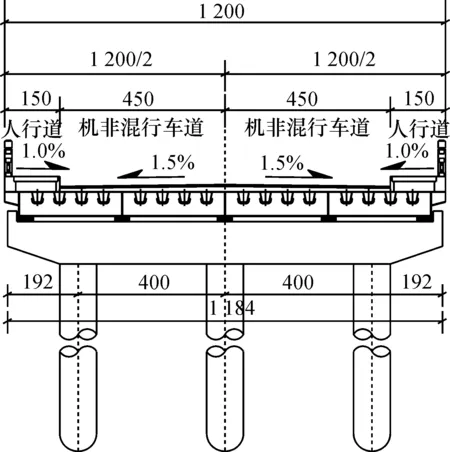
图2 异形钢箱梁断面图Fig.2 Section of the special-shaped box girder bridge

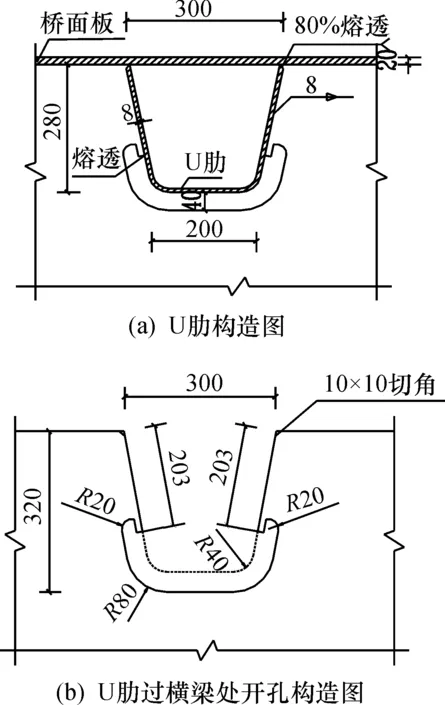
图3 U肋构造细节Fig.3 The structural details of U rib

考虑到驾驶习惯的地域差异，交通情况及转弯的曲线半径可能对横向轮迹分布的影响，选取与背景工程同地区、交通状况相近和曲线半径相同的一处转弯路段进行观测。如图4所示，在转弯起点A，转弯弧线中点B及转弯终点C三处分别设置观测点进行观测，采集2017 年9 月4 日至9 月5 日共计2 800 辆车的样本数据。

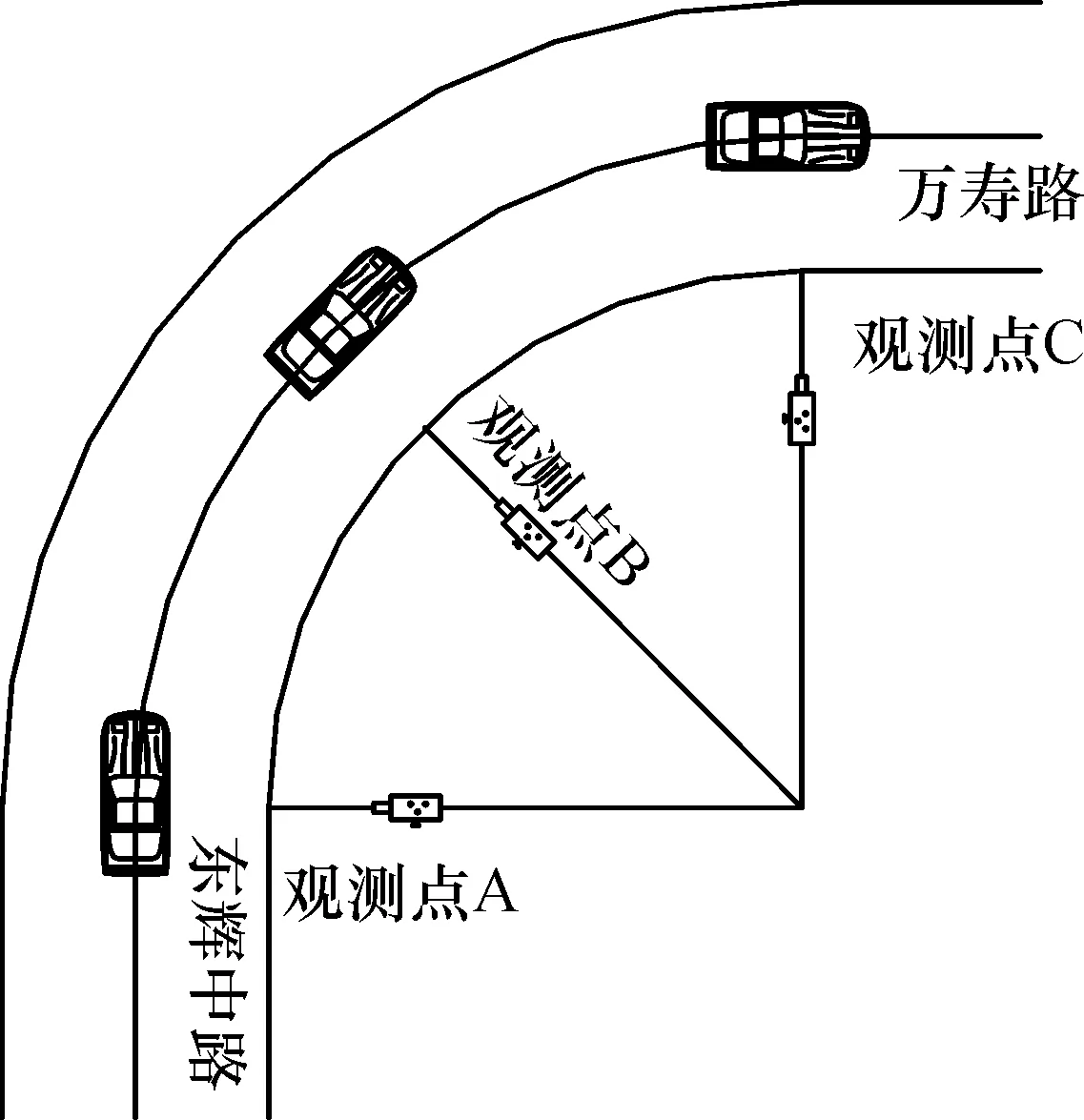
图4 横向轮迹分布观测Fig.4 Observation points in the on-the-spot survey

根据实测数据，车辆轮迹中心线分布在距离车道边缘1.65～3.5 m内，分布宽度为1.6 m，较崔冰等[8]对虎门大桥轮迹横向分布统计得到的宽度范围要大33%，且在车辆转弯的全过程，轮迹横向位置的分布大致相同。按照15 cm的横向间隔区间对实测得到的轮迹中心线的分布宽度范围进行划分，共计划分11 个区域，如表1所示，区域划分示意图如图5所示。

表1 轮迹横向分布宽度区域划分Table 1 Zooning division of transverse distribution width of wheel track mm

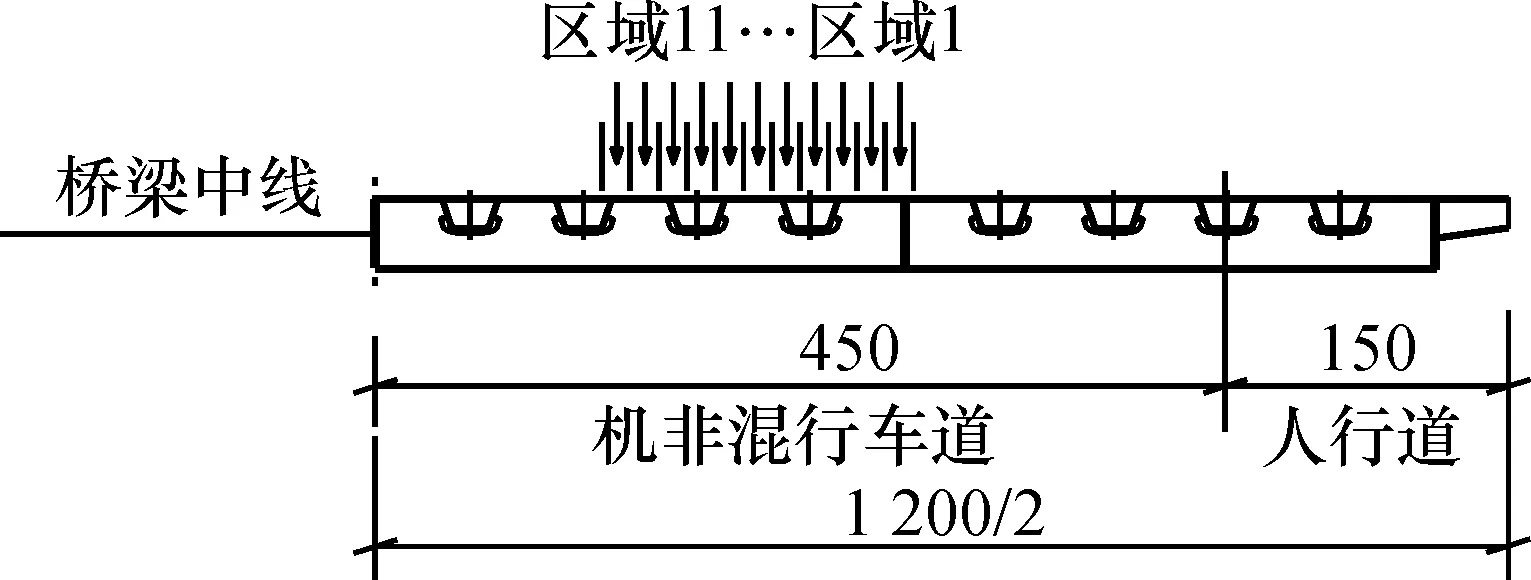
图5 区域划分示意图Fig.5 Diagram of the zooning division

统计A，B，C三处观测点车辆轮迹中心线在横向各个区间的分布频率，其结果如图6所示，取三处观测点的平均值作为该转弯车道横向轮迹分布频率的代表值，如图7所示。从图6可以看出：车辆轮迹中心线在距离车道边缘230～ 245 cm的区间内分布最为集中，分布频率为30.9%，较直行时轮迹最集中处的频率值大40.4%，呈现出更强的集中性。

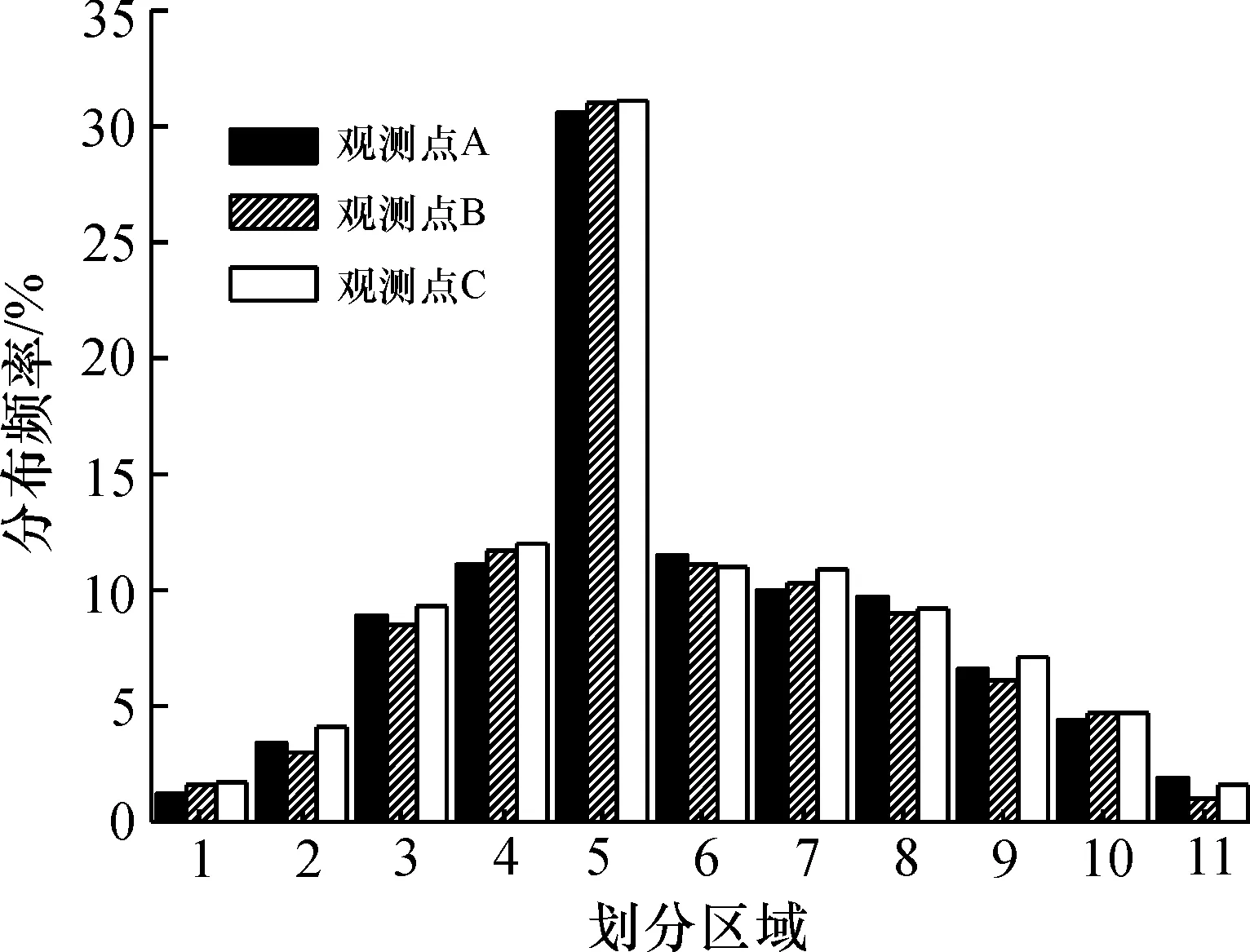
图6 各观测点处轮迹横向分布频率图Fig.6 Frequency of transverse distribution of wheel track at observation points

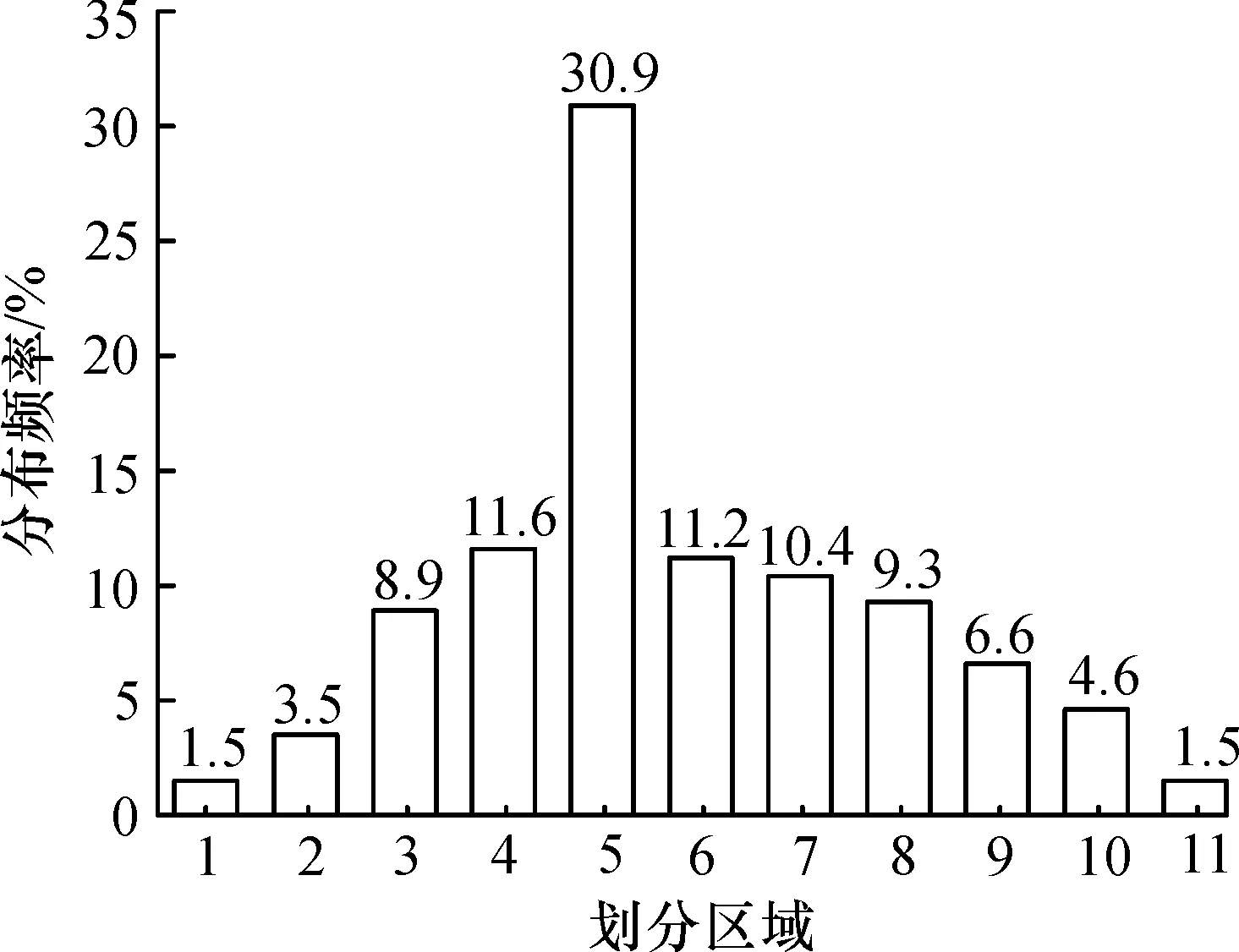
图7 轮迹横向分布频率平均值Fig.7 Average frequency of transverse distribution of wheel track

2 异形钢箱梁桥面板模型

为分析车辆右转弯时的横向轮迹分布对异形钢箱梁典型疲劳细节处的疲劳应力幅的影响，采用ANSYS有限元软件建立背景工程的全桥模型，如图8所示。建模过程中各细节参数及板件厚度与原型一致，采用四节点壳单元模拟，单元网格尺寸10 cm，全桥共计176 907 个单元。

国内外对钢结构桥梁的疲劳构造细节进行了大量的调查研究[9-11]，根据其结果，选取如图9所示的A，B，C，D4 种典型疲劳细节进行研究，其中A为U肋与顶板、横隔板相交处，B为U肋与顶板相交处，C为U肋对接处，D为横隔板与U肋相交处。各疲劳细节应力取值位置如表2所示。

图8 异形钢箱梁有限元模型Fig.8 Finite element model of special-shipped steel box girder bridge

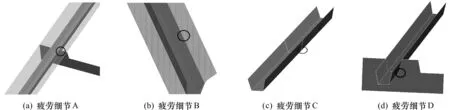
图9 钢结构桥梁疲劳细节Fig.9 Fatigue details of steel structural bridge

表2 疲劳细节应力取值位置Table 2 Stress value position of fatigue structural details

国内在研究轮迹横向分布对疲劳细节应力幅的影响时多忽略车轮之间的相互作用而采用单轮加载，即在横桥向和顺桥向内将单个车轮按实测或规范规定的横向分布区间加载于桥面，再对各个区间所对应的轮迹横向分布频率予以考虑。这种加载方法与桥面的实际车轮的加载形式可能存在较大差异。

为准确反映桥面的实际车辆加载情况，采用规范规定的疲劳荷载计算模型III所对应的标准疲劳车加载，如图10所示，并考虑铺装层对车轮荷载的分散作用。先将标准疲劳车沿着车道中心线纵向移动加载，确定各疲劳细节在桥面纵向的最不利位置，后在纵向最不利位置处按实测轮迹横向分布概率横向加载，确定待观测的A，B，C，D4 个疲劳构造细节分别位于从右转弯车辆驶入桥面算起第5号横梁处机非混行车道下左起第2 个U肋右侧，第5，6号横梁中部机非混行车道下左起第2 个U肋右侧，第5，6号横梁中部机非混行车道下左起第2 个U肋右下侧，第5号横梁处机非混行车道下左起第2 个U肋右下侧。

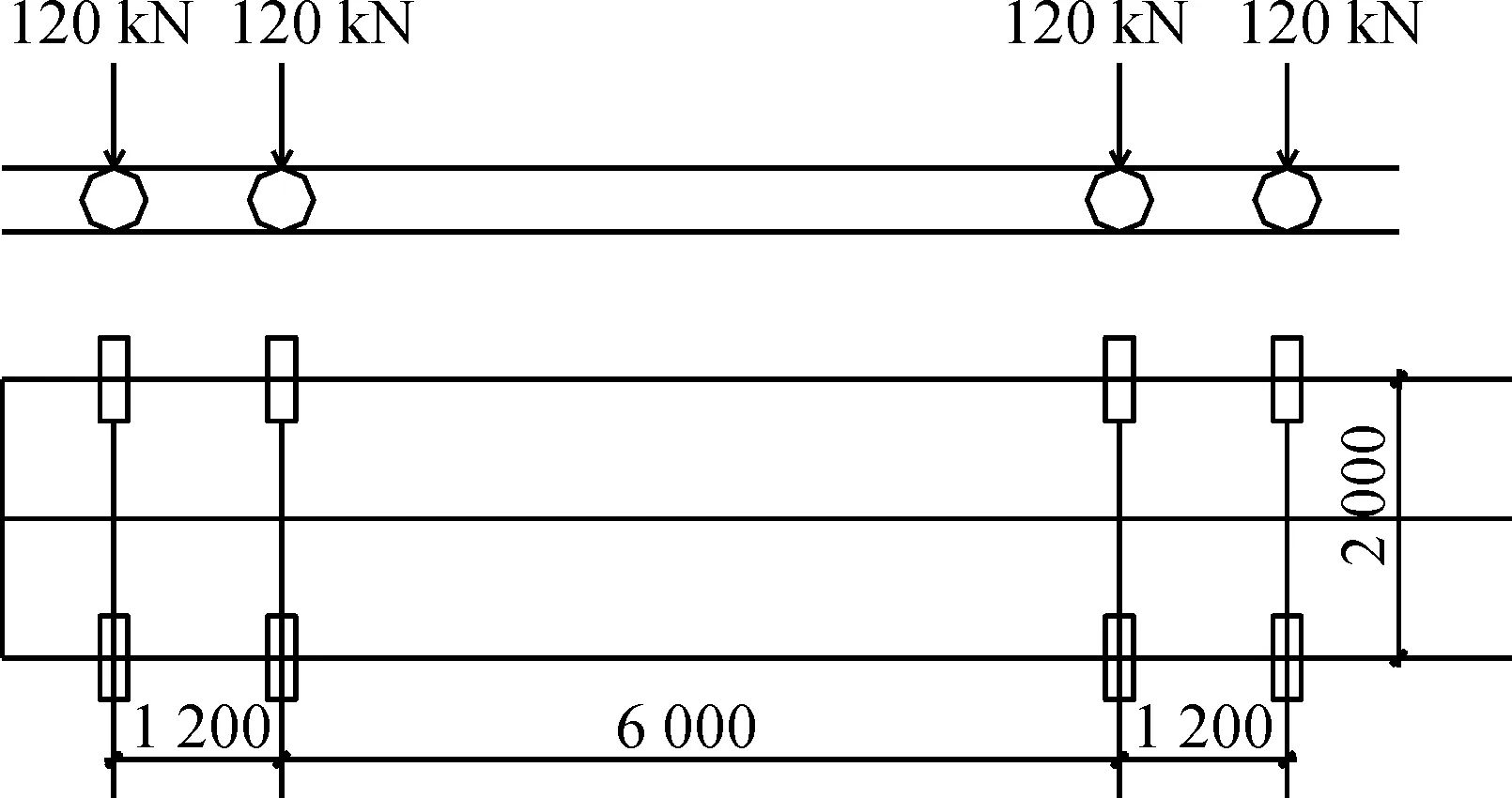
图10 标准疲劳车模型Fig.10 Model of standard fatigue vehicle

3 轮迹横向分布对疲劳应力幅的影响

3.1 实测轮迹横向分布加载下的应力历程

根据实测数据，选取每个区域的中心线为加载迹线，共计11 条加载迹线，即加载迹线1至加载迹线11。由前轮驶入桥面开始，到后轮驶出桥面处结束，每次移动20 cm为一个工况，每条加载迹线分为126 个工况。将标准疲劳车按加载迹线1至加载迹线11及每条加载迹线126 个工况纵横向加载，观测疲劳细节A，B，C，D处应力的变化情况，绘制出应力历程，如图11所示。

图11 实测轮迹横向分布下的各疲劳构造细节应力历程Fig.11 Stress process of fatigue structural details under transverse distribution of wheels based on field survey

3.2 我国桥梁规范轮迹横向分布加载下的应力历程

我国在最新颁布的JTG D64—2015《公路钢结构桥梁规范》中给出了疲劳荷载计算模型III及其相应的车轮横向分布概率，该模型是在欧洲规范疲劳荷载模型3的基础上通过修改车轮着地面积得到的，并按照0.1 m的宽度将轮迹中心线的分布宽度分成了5 个加载区域，分别为加载区域1至 加载区域5，并给出每隔加载区域的横向分布频率，如图12所示。

将上文中各个疲劳构造细节的疲劳影响线中应力数值最大的点所对应的影响线取为加载区域1，加载区域1中心线向两侧横向偏移0.1 m取为加载区域2，加载区域3，加载区域1中心线向两侧横向偏移0.2 m取为加载区域4，加载区域5。车辆轮迹中心线分别位于各个加载区域中心线处，分别为加载迹线1至加载迹线5。每条加载迹线按车辆没移动0.2 m为一个加载工况分为126 个加载工况。A，B，C，D4 个疲劳构造细节在标准疲劳车按照加载区域及加载迹线纵横向加载过程的应力历程如图13所示。

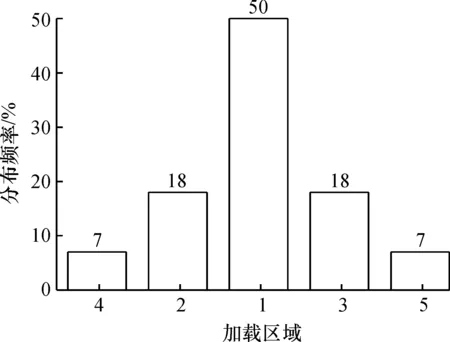
图12 轮迹横向分布模型Fig.12 Model of transverse distribution of wheels stipulated in the code

图13 轮迹横向分布下的各疲劳构造细节应力历程Fig.13 Stress process of fatigue structural details under transverse distribution of wheels based on the code

由图11，13可知：对于某个疲劳细节的单条迹线加载时的应力历程曲线，标准疲劳车在纵向加载过程中，车轮纵向距疲劳构造细节位置较大时，其应力较小，在车轮驶近该位置过程中，应力逐渐增加，且应力增加的幅度随着车轮荷载的接近逐渐增大，应力历程曲线随着车辆前后轮的驶近—碾压—驶离的过程中呈现增大—达到峰值—减小的趋势；对于某个疲劳细节的所有11条迹线加载时的应力历程曲线，曲线形状保持相似，但其峰值却随着加载迹线距横向最不利位置的远近而呈现出较大变化，当距离最近时峰值最大，距离最远时峰值最小。由分析可知，在车辆右转弯时，桥面板典型疲劳构造细节的疲劳应力幅受轮迹横向分布的影响十分显著。

3.3 等效应力幅

为考虑车辆横向分布对各个疲劳构造细节处应力幅的贡献，根据实测横向分布概率及、加载迹线下的应力历程，按Miner线性累积损伤原理计算疲劳构造细节A，B，C，D处的等效应力幅，其计算式为

(1)

式中：Δσeq为等效应力幅；pi为第i种车轮横向位置所对应的频度；Δσi为第i种疲劳细节应力幅；m为应力幅曲线斜率参数，一般取3.0。

实测横向轮迹分布及规范横向轮迹分布下按照式(1)计算得到的等效应力幅如表3所示。

表3 实测及规范横向轮迹分布下的等效应力幅Table 3 Equivalent stress range based on transverse distribution of field survey and the code MPa

由表3可知： A，B，C，D 4 种疲劳构造细节在实测轮迹横向分布下，其等效应力幅分别是最大应力幅的0.87倍、0.80倍、0.82倍和0.86倍；而在规范轮迹横向分布下4 种疲劳构造细节分别是最大应力幅的0.93倍、0.93倍、0.92倍、0.92倍。选取的4 种疲劳构造细节在采用实测轮迹横向分布模型时计算的等效应力幅均小于使用规范规定的轮迹横向分布模型时计算的等效应力幅，分别是后者的0.93倍、0.86倍、0.89倍、0.90倍。

4 结 论

车辆在右转弯过程中，虽然其轮迹中心线的分布宽度较直行时大，但却在某个横向分布区间内表现出更大的集中性。由于这种集中性，如果轮迹分布宽度相同，车辆右转弯比直行时对疲劳构造细节处应力幅的影响更大。标准疲劳车在不同的横向加载区域内加载时，其应力历程曲线形状保持相似，但其峰值却随着加载迹线距横向最不利位置的远近而呈现出较大变化，当距离最近时峰值最大，距离最远时峰值最小。在车辆右转弯时，桥面板典型疲劳构造细节的疲劳应力幅受轮迹横向分布的影响十分显著。A，B，C，D 4 种疲劳构造细节在采用实测轮迹横向分布模型时其等效应力幅均小于使用JTG D64—2015规范规定的轮迹横向分布模型时计算的等效应力幅，分别是后者的0.93 倍、0.86 倍、0.89 倍、0.90 倍，所以在实际工程中，考虑右转弯车辆轮迹对异形钢箱梁疲劳构造细节应力幅的影响时，用规范的轮迹横向分布模型是偏于安全的。