相位平滑伪距对GNSS定位精度的影响
2018-12-03程鹏飞成英燕
王 涛,程鹏飞,成英燕
(1.辽宁工程技术大学,辽宁 阜新 123000;2.中国测绘科学研究院,北京 100830)
0 引言
全球卫星导航系统(global navigation satellite system,GNSS)具有全天候、连续性、全球覆盖等优势[1],所以GNSS在测量领域、军事、交通运输、大气科学、农业及资源调查等领域被广泛应用。精密星历精密钟差产品精度提高,延迟时间缩短。在GNSS各种定位模式中,GNSS解算精度与观测值的质量密切相关。GNSS观测过程中的测量误差包括卫星、接收机、传播路径上的测量误差。这些误差有的可以模型化,有的却不能精确模型化;但是通过各种组合以及差分处理可以消除大部分误差。配合利用事后处理的方式,能计算出更精确的误差项,对研究全球定位系统(global positioning system,GPS)和北斗卫星导航系统(BeiDou navigation satellite system,BDS)特性有重要的实践意义。对于精密单点定位,在定位中需同时采用相位和伪距观测值,并且还需要厘米水平的卫星轨道和达到亚纳秒量的卫星钟差改正值;而双差网解定位对于数据的预处理结果的精度要求则更高。
本文采用相位平滑伪距的方法来获取观测数据进行解算,以期能够有效提高精密单点定位结果,并获得高精度的双差网解结果。
1 相位平滑伪距方法
相位平滑伪距包含载波相位周跳探测与修复功能和平滑伪距功能[2],其包含了MW线性组合、无几何线性组合和无电离层组合。其中MW是伪距与载波观测值之间的线性组合,电离层延迟、卫星钟差、接收机钟差和卫星至接收机之间的几何距离利用此组合都可以被消除,并探测出含有周跳的弧段;无几何相性组合则对该弧段探测出载波L1和载波L2上的周跳大小;再利用无电离层组合进行粗差探测并剔除来使得数据质量增高;最后利用修复好的载波相位观测值进行伪距平滑,平滑后的伪距观测值将进行接收机钟同步以大大提高计算结果精度:经过相位平滑伪距之后使得精密单点定位结果和双差网解结果精度提高。其数据处理策略与流程如图1所示,图1中RMS(root mean square)为均方根误差。
1.1 MW线性组合
MW线性组合公式为

(1)
式中:L6为MW线性组合值;L1、L2为载波相位观测值;f1、f2分别为L1、L2载波上的频率;P1、P2为伪距观测值。
利用MW线性组合,电离层延迟、卫星钟差、接收机钟差和卫星至接收机之间的几何距离都可以被消除,并探测出含有周跳的弧段。如果MW线性组合的均方根值有小于0.5L5个周期,则说明存在周跳或者异常值。该方法也有一种特殊情况探测不出周跳,那就是当在2个频率上的周跳整周数是相同的时候,则此方法无效。在探测周跳和粗差时,首先计算一个弧段内所有MW组合观测值的RMS值,如果大于定义的阈值,
则认为该观测弧段存在周跳,否则对下一个观测弧段进行探测。观测弧段 MW 组合RMS的计算采用公式为
(2)
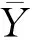
具体算法为:将观测弧段分为等长的2个子弧段,其中 RMS 大的子弧段称为子弧段1包含周跳,另一弧段称为子弧段2不含周跳或者包含较小的周跳。从靠近子弧段2一端的历元开始,检查弧段1中所有历元,如果某个历元的值与子弧段2的均值之差大于周跳判定阈值,则确定该历元处发生了周跳。以周跳发生历元为分界点,将该观测弧段分为2个新的子弧段。如果新子弧段的RMS大于阈值,则以大于3倍均方根为标准,对该弧段的粗差进行探测并标记,直到子弧段的RMS值小于规定的阈值。最后再以2个新子弧段的均值之差作为周跳估值并且修正周跳,修正之后再将2个新子弧段连接。去除标记的粗差,从新计算整个连续观测弧段的RMS进行周跳探测,直至探测不出周跳为止。最后,重新对整个观测弧段以大于4倍均方根为阙值进行粗差探测。
1.2 无几何组合
双频相位观测值的无几何(geometry-free)模式只包括电离层延迟和模糊度,由于在短时间内电离层延迟变化浮动较小,因此周跳探测过后,利用无几何组合估计发生周跳的观测弧段中L1和L22个频率上的周跳大小。上一步利用MW组合确定周跳发生位置后,利用周跳发生前的m个无粗差观测量获得一组多项式系数,计算周跳处L4组合值为W1,利用周跳后的m个无粗差观测量获得的周跳处的L4组合值为W2,公式为
W2-W1=λ1·Δb1-λ2·Δb2
(3)
式中:W1和W2分别是周跳前后的L4组合值;λ1、λ2分别是2个频率上的载波;Δb1和Δb2分别是2个频率上的周跳。算出周跳大小之后,进行周跳修复。
1.3 无电离层组合
有时由于程序中可能会带来一些系统误差,会直接导致MW组合不能完全探测出观测数据中的周跳及粗差,因此引入消电离层组合进行更深一步的数据质量检查。伪距和相位的消电离层组合相减为
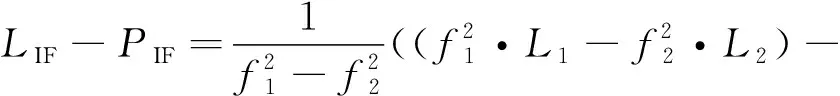
(4)
式中LIF和PIF分别是相位和伪距观测值。
式(4)中只包含模糊度和噪声这2项,采用无电离层组合对观测数据作进一步的粗差探测,直至没有粗差为止。该组合的不足之处在于噪声比较大,具体为伪距P码的3倍,MW组合的4倍。但对去除系统性影响造成的误差仍然比较有效。
1.4 相位平滑伪距
最后一步包括平滑的码观测值。以前的程序步骤已经清除了码和相位观测数据。这使我们能够平滑的码观测值使用载波相位观测。对于码平滑的码观察在一个干净的观察弧实际上被替换的相位观测。公式为
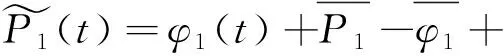
(5)
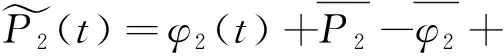
(6)
2 相位平滑伪距对GNSS定位影响实验与精度分析
为了考察相位平滑伪距对GNSS定位影响,本次实验利用自己编写的相位平滑伪距程序来进行数据处理,采用相位平滑伪距后获得的观测值并用相同的定位软件中解算定位结果部分来算取的动态伪距单点定位和动态精密单点定位结果,这样可以分析每个历元平滑后获取的动态伪距定位和动态精密单点定位结果的精度情况,并解算出平滑后精密单点定位坐标和原定位软件数据处理后得出的精密单点定位坐标进行对比分析。以相位平滑伪距解算国内5个国际GNSS服务(international GNSS service,IGS)分析中心参考站的精密单点定位结果和双差网解结果与对应网站上公布的IGS坐标进行对比分析。实验中的数据采用5个IGS站处理时段为2016年年积日第80天数据,5个IGS站分别为:BJFS、CHAN、SHAO、ULAB、WUHN。
2.1 动态伪距定位与动态精密单点定位影响结果分析
采用北京房山站(BJFS)2016年年积日第80天的数据,利用相位平滑伪距获得的观测文件进行动态伪距定位和动态精密单点定位并获取点位残差,利用IGS提供的BJFS站的坐标值(参考框架为ITRF2014)作为基准值与解算结果进行对比[3]。结果如图2~图5所示。
由图2可知,利用经过相位平滑伪距后获得的观测值进行动态伪距单点定位,结果是X方向外符合精度为0~0.9 m、Y方向外符合精度为0~0.5 m和Z方向外符合精度为0~0.9 m,这个结果要比通常情况下计算的伪距单点定位结果高出一个数量级。通过图3和图4可知,未经过相位平滑伪距后获得的观测值进行动态伪距单点定位,结果残差值为-8~8 m,而用平滑过后获得的观测值进行动态伪距单点定位结果残差值为-0.8~0.8 m。由图5可知,利用经过相位平滑伪距后获得的观测值[4]进行动态精密单点定位,结果是X方向外符合精度为0~0.04 m、Y方向外符合精度为0~0.02 m和Z方向外符合精度为0~0.04 m。
2.2 精密单点定位和双差网解影响
采用BJFS、CHAN、SHAO、ULAB和WUHN 5个IGS站的数据,处理时段为2016年年积日第80天,分别解算精密单点定位结果[5-7]和双差网解结果[8-9]。利用相位平滑伪距获得的观测文件和通常定位软件数据预处理后的观测值分别进行精密单点定位,将以上2种精密单点定位结果与IGS提供的坐标值(参考框架为ITRF2014)作差再进行对比,结果如图6~图10所示。
利用相位平滑伪距获得的观测文件和通常定位软件数据预处理后的观测值分别进行精密单点定位,并对比其外符合精度[10-11],结果可由图6看出,前者比后者的精度要高出0.5~1.5 cm。通过图7和图8可知,相位平滑伪距后的5个IGS站精密单点定位3个方向的内符合精度在2 mm以内、外符合精度在3 cm以内。通过图9和图10可知,相位平滑伪距后的5个IGS站双差网解定位3个方向的内符合精度在1.5 mm以内、外符合精度0~1.3 cm。可见相位平滑伪距可以显著提高精密单点定位解算的精度,并且可以获得较高解算精度的双差网解结果。
3 结束语
采用相位平滑伪距对原始观测文件进行平滑后,可有效提高精密单点定位解算的精度[12],并且可以获得较高解算精度的双差网解结果。从动态伪距单点定位结果可以看出,X方向外符合精度为0~0.9 m、Y方向外符合精度为0~0.5 m和Z方向外符合精度为0~0.9 m;动态精密单点定位结果在X方向外符合精度为0~0.04 m、Y方向外符合精度为0~0.02 m和Z方向外符合精度为0~0.04 m。在对比相位平滑伪距获得观测文件解算出的精密单点定位的结果与通常定位软件数据预处理后的观测值进行精密单点定位的结果后可知,前者精度要比后者高出0.5~1.5 cm。双差网解定位结果在3个方向的内符合精度为1.5 mm以内,而外符合精度为0~1.3 cm。本文结果可为对GNSS数据处理精度要求不断提高的行业和领域提供参考。
