思想，赋予数学课堂生长的力量

郑秋杰

【摘要】数学课程不仅仅教会学生数学知识技能，更重要的是让学生获得数学思想。如何使学生获得数学的基本思想成为数学课程的重要目标。在数学思想中，“最重要的，首推函数的思想”。在小学中谈函数思想，主要应该注重些什么呢？

【关键词】基本思想

课堂生长

活动经验

《义务教育数学课程标准（2011年版）》指出：“通过义务教育阶段的数学学习，学生能获得适应社会生活和进一步发展所必需的数学的基础知识、基本技能、基本思想、基本活动经验。”为此，使学生获得数学的基本思想成为数学课程的重要目标。数学课程不仅仅教会学生数学知识技能，更重要的是让学生获得数学思想。

一、数学思想教学的现状分析

1.缺乏认识，数学思想被架空

苏教版四年级下册“三角形高的画法”的教学中，一位教师通过情境让学生形象地认识三角形的高后，让学生自己画出给定三角形的高，交流时确定在“一靠底二平移三画线”的操作方法上。这样的教学架空了学生之前“画垂线”的经验，架空了学生通过“画垂线”得到“画高”的数学思想。

2.认知偏差，数学思想被“方法”

课程标准的措辞是数学的“基本思想”，而不是数学的“基本思想方法”，所以一些数学化的程序、步骤等操作方法不可称为数学思想。如小数除法的计算，过程中所涉及的方法，它们属于更为具体的层次。

3.理解不透，数学思想被“复杂”

有效的数学思想的渗透是一种深入浅出的教学。苏教版二年级上册《简单实际问题（复习）》这课，教师通过让学生根据编写加减乘除法的算式，进一步巩固学生对加减乘除法的算理的认识，然后请学生将这四种算法进行分类，意图得到乘法（除法）是加法（减法）的简便计算。但对于二年级的学生，很难说清楚为什么这样分类，教师落实分类思想的意图受到了阻碍。

二、数学的基本思想分类梳理

数学思想很多，有些思想是从一些基本思想派生出来的，所以数学思想间具有层次性，主要有以下三部分。

1.数学抽象的思想

“人们把外部世界与数学有关的东西抽象到数学内部，形成数学研究的对象。”因此，学习数学必然要学会数学抽象。如学生通过摆小棒的过程抽象出除法算式：10÷3=3……1（支），理解有余数的除法的意义。借助生活中的情境抽象出图形（如三角形、平行四边形、圆形等），通过对图形的研究认识为什么生活中的物品设计成这种形状。由抽象思想派生出来的有：分类的思想，集合的思想，数形结合的思想，等等。

2.数学推理的思想

课程标准指出：“推理是数学的基本思维方式，也是人们学习和生活中经常使用的思维方式。”推理是从一个或几个已有的判断得出另一个新判断的思维形式。推理分为两种形式：演绎推理和合情推理，小学数学中主要是学习合情推理。苏教版五年级下册利用公因数和公倍数解决实际问题的思考过程就是一种推理的过程。由推理思想派生出来的有：归纳的思想，演绎的思想，公理化的思想，转换化归的思想，等等。

3.数学建模的思想

人民教育出版社课程教材研究所王永春教师认为：“数学模型是用数学语言概括或近似地描述现实世界事物的特征、数量关系和空间形式的一种数学结构。从广义的角度讲，数学的概念、定理、规律、法则、公式、性质、数量关系等都是数学模型。”数学模型是沟通数学与现实世界的桥梁，由建模的思想派生出来的有：简化的思想，量化的思想，函数的思想，等等。

三、数学思想的教学策略一以函数思想为例

数学家张景中在《感受数学思想的力量》這篇写给小学数学教师的文章中说道：“小学生学的数学很初等，很简单。尽管简单，里面却蕴含了一些深刻的数学思想。最重要的，首推函数的思想。”那么，函数思想的本质是什么呢？有人是这样认为的：“函数思想是一种考虑对应、考虑运动变化、相依关系，以一种状态确定地刻画另一种状态，由研究状态过渡到研究变化过程的思想方法，函数思想的本质在于建立和研究变量的对应关系。”

1.在“数与代数”中体验函数思想

数学往往尝试着用自己的语言揭示事物中“不变”的内容，抽象它的数学本质，建立符合规律的模型。

在“千课万人”第二届全国小学数学新常态课堂研讨观摩会上，刘松老师执教的《倍的认识》中出示了这样一个情境：黄花有2朵，红花有6朵；黄花有4朵，红花有12朵（如图1）。红花的朵数随着黄花的朵数发生了变化，但不变的是“红花是黄花的3倍”这一数量之间的关系。所以刘老师随即将黄花抽象成1份，红花就可以看作这样的3份（如图2），将这一现象用数学语言表达成：红花是黄花的3倍。如果抽象成函数解析式的话，y代表红花朵数，x代表黄花朵数，即得到y=3x，y随着x的变化而变化。虽然学生暂时不懂函数，但在这一过程中体会到了数学能表达事物之间的联系，把握“变”中的“不变”，才能把握事情变化的规律。

2.在“图形与几何”中体验函数思想

在小学数学课中，不仅在“数与代数”中渗透着函数思想，“图形与几何”中的位置与变换也渗透着函数思想。两个集合的“一一对应关系”，把握对应的规则，即能感受到研究图形的价值。

苏教版五年级上册教学《三角形面积的练习》这—课时，教师设计了以下几个环节引导学生探究：

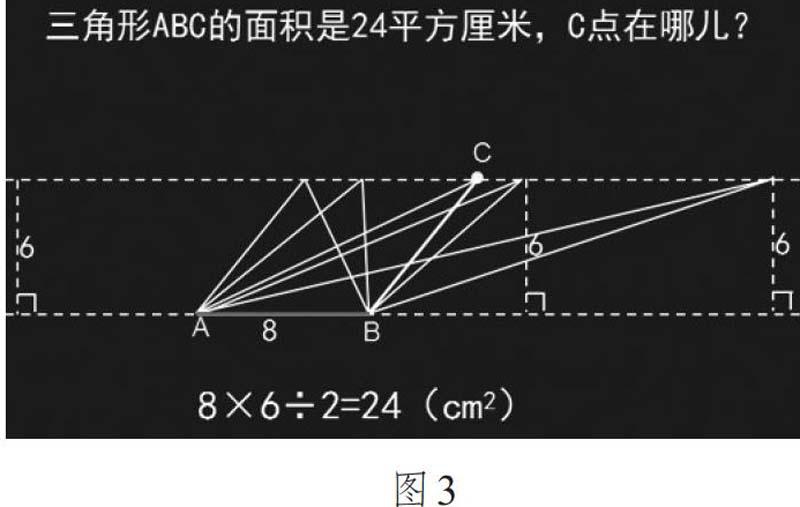
（1）思考：三角形ABC的面积是24平方厘米，C点在哪里？

预设一：左上顶点、右上顶点。（追问：三角形ABC的面积为什么是24平方厘米？）

预设二：上底边上的任意一点。（追问：为什么这几个三角形的面积都是24平方厘米？）

（2）思考：C点只能在底边上吗？

引导得出：上底边无限延长，C点可以是这条直线上的任意一点。

出示两个钝角三角形，比画底和高分别是多少？三角形的面积变吗？

思考：为什么这些三角形的面积都不变？

追问：底是同一条，但是高不是同一条，为什么面积也相等呢？

指出：这些三角形的高就是两条平行线之间的距离（如图3）。

变化是函数思想的精髓，将原本静止的数学问题，转化成变化的问题。通过C点的“动”，感受三角形的变化，但三角形的面积是不变的，思考不变的原因在哪，在解决变化问题的过程中，学生更能体会函数思想。

3.在“统计与概率”中体验函数思想

函数思想无处不在，只要有变化的地方，我们就能寻找变化的规律，用数学语言概括这种规律，形成一种数学认识。在《统计与概率》中，我们所看见的折线统计图本身就是函数图像，如身高随着年龄发生变化、气温随着时间发生变化等。在这些变化中，有的我们已经找到了规律，如小学六年级形成正比例、反比例图像的规律，还有的规律还在探索之中。

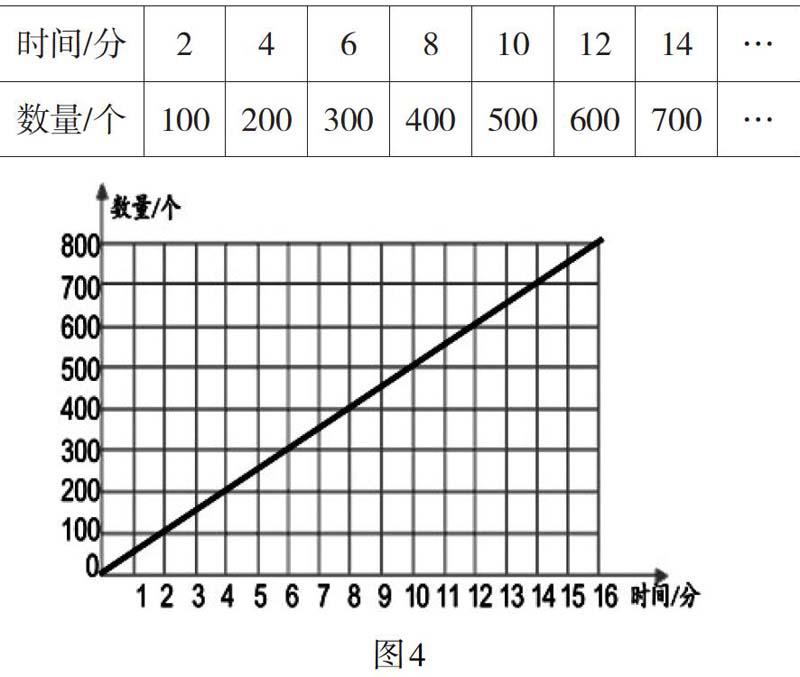
在教学《正比例图像》时，教师通过让学生两次尝试根据表格中给出的两种成正比例的量（如下表）描点等操作进行绘制图形，然后让学生自己选择两个成正比例的数量，设计数据填表后绘制图形（如图4）。在操作中学生发现：画出的图是一条直线。在这个过程中，一方面，学生感受到当一个量变化时，另一个量也在变化，但是它们的比值是不变的，这个数量之间的关系在图像上清晰地表现成一条直线；另一方面，学生还可以明确地感受到数量之间的关系除了能用形如这样的表达式表示，也可以用图像表示。

函数思想如何渗透在我们的教学中，如何发掘教学内容的渗透点，这是我们教师应该思考的问题。笔者认为：越是简单的内容，内涵越是丰富，只要有“变化”的地方，就蕴含着函数思想，不需要教师告诉学生这是函数思想，但渗透后的数学学习就会有生长的力量。