超高阶重力场模型最小二乘快速实现

田家磊，李新星，吴晓平，邢志斌

1. 信息工程大学地理空间信息学院，河南 郑州 450001； 2. 63850部队，吉林 白城 137000； 3. 武汉大学测绘学院，湖北 武汉 430079

地球重力场模型是对地球重力场地面和空间观测数据实施数学上的解析逼近的结果，在大地测量学、地球物理学、地震学、地质学、海洋科学、国防科学、空间科学中的应用非常广泛[1-5]。利用重力场模型和相应的球谐展开式可以计算多种扰动重力场元(重力异常、扰动重力、垂线偏差、大地水准面高等)[6-8]。为了获得高精度、高分辨率的地球重力场模型，国内外众多机构投入了巨大的人力、物力与财力[9-10]，目前地球重力场模型已经发展到2159完全阶次[11]。2008年美国国家地理空间情报局(US National Geospatial-Intelligence Agency)发布了目前应用范围最广、高精度超高阶地球重力场模型EGM2008[12-13]。2014年德国地学研究中心(Geo Forschungs Zentrum)和法国空间大地测量组(Groupe Recherches Geodesie Spatiale)联合发布了EIGEN(European Improved Gravity Model of the Earth by New Techniques)系列模型中的最新模型EIGEN-6C4[14-16]。这两个模型是目前普遍采用的超高阶重力场模型。

卫星重力数据用来解算地球重力场模型的中低阶部分，地面与海洋重力数据用来解算地球重力场模型的高阶部分[17-19]。目前重力场模型位系数的求解方法主要有两种：数值积分方法(numerical quadrature，NQ)又称调和分析方法，还有最小二乘方法(least squares，LS)。联合卫星重力资料确定中低阶位系数的方法也有多种，包括基于原始观测数据的处理和基于卫星重力场模型位系数的处理，其中利用最小二乘方法解算位系数的法矩阵叠加方法更具有优势，能够更加详细地顾及地面数据和卫星观测数据之间的权重关系[20]。采用最小二乘方法构建超高阶重力场模型过程中，观测方程中的未知数(模型位系数)和观测值数量大，相应的法方程规模巨大，大型法方程的构建与直接求解难以实现[21-23]。目前国内外利用最小二乘方法计算超高阶重力场模型，均使用超算机或者采用集成计算机网络，基于并行算法进行的，计算成本高，耗时长[24-25]。基于最小二乘方法在求解超高阶模型问题上的优势和面临的难题，本文探索该海量计算过程中难题的解决方案，力争实现超高阶重力场模型的小存储、高效率的解算。

1 块对角最小二乘的基本原理

重力异常与位系数之间关系的基本数学模型为[6]

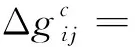
(1)

最小二乘方法可得位模型系数的解及相应的协方差阵[20]

(2)

根据式(1)，矩阵A的各个元素由式(3)和式(4)表示

(3)

(4)

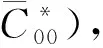
当重力数据分布于整个旋转椭球面、数据在经度方向分辨率一致、数据的权与经度无关且关于赤道对称时，权矩阵P是个对角阵，因此法矩阵N=ATPA可表示为

(5)

为方便研究，本文近似权矩阵P为单位阵，根据球谐函数的正交特性知，由以上观测方程得到的法方程矩阵N是一稀疏矩阵，即

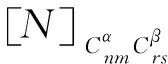
(6)

(7)

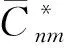
以2160阶次重力场模型前2159阶位系数的最小二乘方法求解为例，Nmax=2160，系数矩阵列分块个数以及生成的法矩阵块个数均为4×2159，法方程的求解可简化为对4×2159个法矩阵分别求解。这些法矩阵块中最大的块为int(Nmax/2)×int(Nmax/2)，即1080×1080，因此最大的系数列块矩阵A1的大小为(2160×4320)×1080，存储A1需要75.1 G的空间，因此对于普通性能的计算机，块对角化后的超高阶模型求解仍面临存储难题。

2 块对角化最小二乘方法的改进

2.1 法矩阵约化求解

由上述分析可知，利用分块矩阵求解法矩阵，可简化为对一个块的求解

(8)

利用式(8)求解法矩阵过程中，需要存储系数列块矩阵At，最大的At矩阵为A1，存储该矩阵需要75.1 GB空间，较难实现，针对此问题，试分析矩阵At的特点，寻找简化方法。At可表示为式(9)、式(10)两种形式之一

(9)

(10)

由上述公式可看出，矩阵At具有极强的规律性，为简化矩阵计算，设

(11)

(12)

则可得

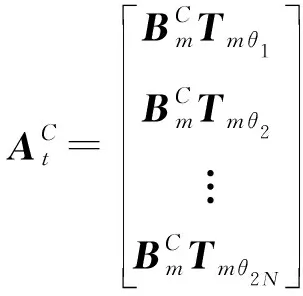
(13)

则法矩阵Nt的计算如下

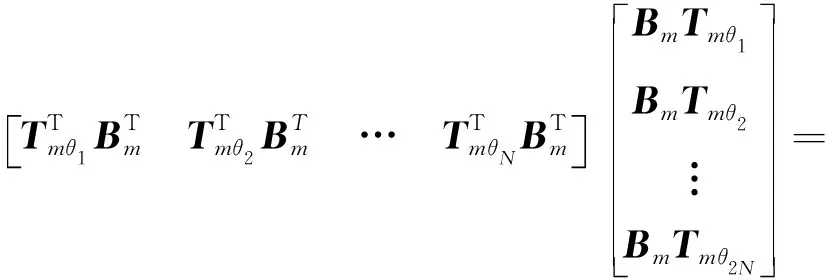
(14)

综合式(11)、式(12)，可得Nt的表达式为

(15)

因为格网重力异常分布是按照全球等角格网分布的，即经度间隔是一致的，可得

(16)

则

(17)

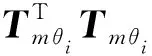
对于求解2160阶次的超高阶重力场模型而言，使用5′×5′格网重力异常，共计2160个纬度值，因此所有Tm θi值的存储量为2160×1080，即需要开辟17.8 MB的空间。综上所述，经过块对角化以及本文提出的法矩阵快速计算方案，求解一法矩阵的过程，大大节约了存储空间，提升效果见表1。

表1块对角以及法矩阵约化求解方法对存储量改进的效果统计表

Tab.1Astatisticaltableoftheimprovementofthestorageobtainedbythemethodofblockdiagonalandmatrixreduction

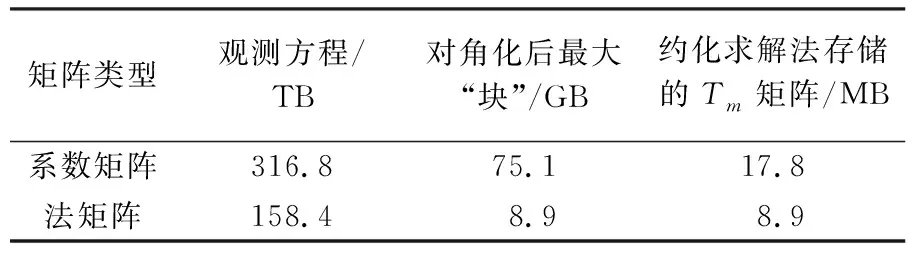
矩阵类型观测方程/TB对角化后最大“块”/GB约化求解法存储的Tm矩阵/MB系数矩阵316.875.117.8法矩阵158.48.98.9

由表1可知，经过待求位系数的重新排序的块对角化以及法矩阵约化求解改进后，使得系数矩阵和法矩阵的必要存储空间有了大幅度的缩减，使得计算变得简单高效。

2.2 Legendre函数计算存储策略

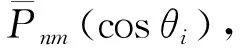
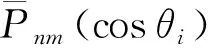
对于2160阶次的重力场模型求解，当一次性存取所有的Legendre函数值，需要存储变量个数为2160×(2159×2164)/2，对应的存储空间37.6 GB，这么大的数据量很难使用内存存储，如果写入文件进行读取的话会大大降低计算效率。如果每求一个At矩阵便遍历求解一次legendre值，那么需要循环计算次数为2160×4，这也将大大降低计算效率。

图1 Legendre递推示意图[3]Fig.1 Legendre recursive sketch map[3]

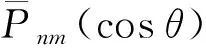
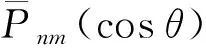
2.3 Legendre函数对称性

通过对系数矩阵At进行分析可知，当n-m为偶数时，At矩阵上半部分与下半部分是对称的，当n-m为奇数时，At矩阵上半部分与下半部分数值相等，但符号相反。究其原因，是由于全球格网数据分布是关于赤道对称的，满足θi=π-θN-1-i，且缔合Legendre函数满足以下特性

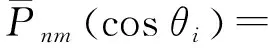
(18)

因此在计算矩阵At及法矩阵时，只需要计算上半部分即可，最终求得的法矩阵N乘以2即为最终的法矩阵，该方法能够节省一半的存储空间及一半的计算时间。

3 试验及分析

3.1 精度改进

采用上述改进的计算方法和存储方式，利用EGM2008模型2159阶位系数模拟计算全球5′×5′格网重力异常点值数据，实现2159阶次超高阶重力场模型的最小二乘方法实现，并与EGM2008模型前2159阶位系数进行比较，作为模型恢复方法精度的衡量标准，并与轮胎调和分析方法恢复重力场模型的精度进行对比分析[26]，结果见图3。图3分别统计了两种方法恢复的模型系数与EGM2008系数差的绝对值的自然对数。

使用EGM2008作为标准模型，计算两种方法恢复的2159阶模型系数的误差阶RMS并进行比较，比较结果见图4，其计算公式为[3]

(19)

由图4可看出，块对角最小二乘方法恢复模型系数的误差阶RMS明显小于使用数值积分方法恢复的模型系数，最小二乘方法恢复的模型整体精度比数值积分方法高出至少5个数量级。

3.2 效率改进

为验证本文所提改进方法在构建全球重力场模型的优势，使用3.2 GHz主频、2 GB内存PC计算机，基于vs2008试验平台，进行模拟计算。

试验统计了分别使用3°×3°、1°×1°、30′×30′及5′×5′的格网重力异常数据，利用传统块对角最小二乘法恢复59阶、179阶、359阶和2159阶次模型的计算时间，并利用改进后的最小二乘方法进行同样的计算，统计结果见表2。

如表2所示，采用块对角最小二乘方法计算模型位系数，效率相对低下，计算359阶位系数需要近2 h，对于2159阶重力场模型，由于其系数矩阵At存储量庞大，无法实现系数的求解。相比传统块对角最小二乘法，采用改进后的方法计算效率有了明显提升，与恢复359阶模型使用2 h相比，改进方法只需要20 s。更重要的是，改进后的方法实现了2159超高阶重力场模型的求解，耗时不足2 h。

表2最小二乘方法恢复重力场模型时间

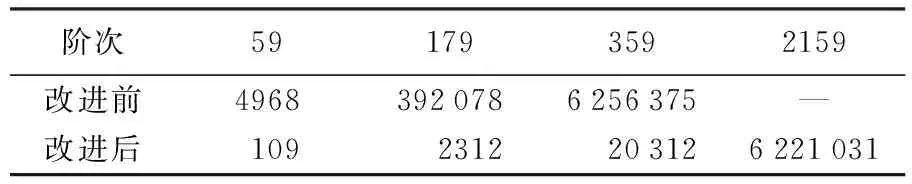
Tab.2 Time of recovering geopotential modelby least-squares method ms

综上，改进后的最小二乘方法不仅实现了普通计算机上超高阶模型的位系数求解，并且效率得到了大的提升。

3.3 数据的精度估计

为了说明相比数值积分方法，最小二乘方法在精度评估方面的优势，本文对EGM2008模型前359阶位系数模拟的30′×30′格网重力异常加入白噪声，利用最小二乘方法恢复模型位系数过程中，记录VTPV的估计值，利用式(20)可获取观测值的单位权中误差

(20)

式中，n为观测量个数；t为未知数个数。

通过对上述30′×30′重力异常数据分别加入5×10-5m/s2和10×10-5m/s2白噪声后，进行模型位系数的恢复，最终得到的统计结果见表3。

表3 精度估计情况统计

根据表3结果可知，最小二乘方法能够在一定程度上反映出数据与模型的吻合程度，即一定程度上评估数据的精度情况，这是最小二乘相对于数值积分方法不可比拟的优势。

4 结 论

数值积分方法实质上就是法矩阵为对角阵的最小二乘方法，即认为模型系数之间均是不相关的，协方差均为0，而块对角最小二乘则估计了同次不同阶系数之间的相关性，其更符合实际情况，也能够恢复更高精度的重力场模型。数值积分方法不能对重力异常数据进行精度评估，块对角最小二乘方法可以。相比数值积分方法，最小二乘方法无法求解Nmax阶系数，例如5′×5′分辨率的格网重力异常只能求解2159阶次的系数，第2160阶的系数必需使用数值积分方法才能求得。另外，数值积分方法使用的重力异常数据通常为点值，即包含全频段信号，所反演的系数才是实际模型位系数，而最小二乘方法所使用的格网重力异常数据应只包含所求阶次的能量，否则其信号在位系数之间会发生泄漏。

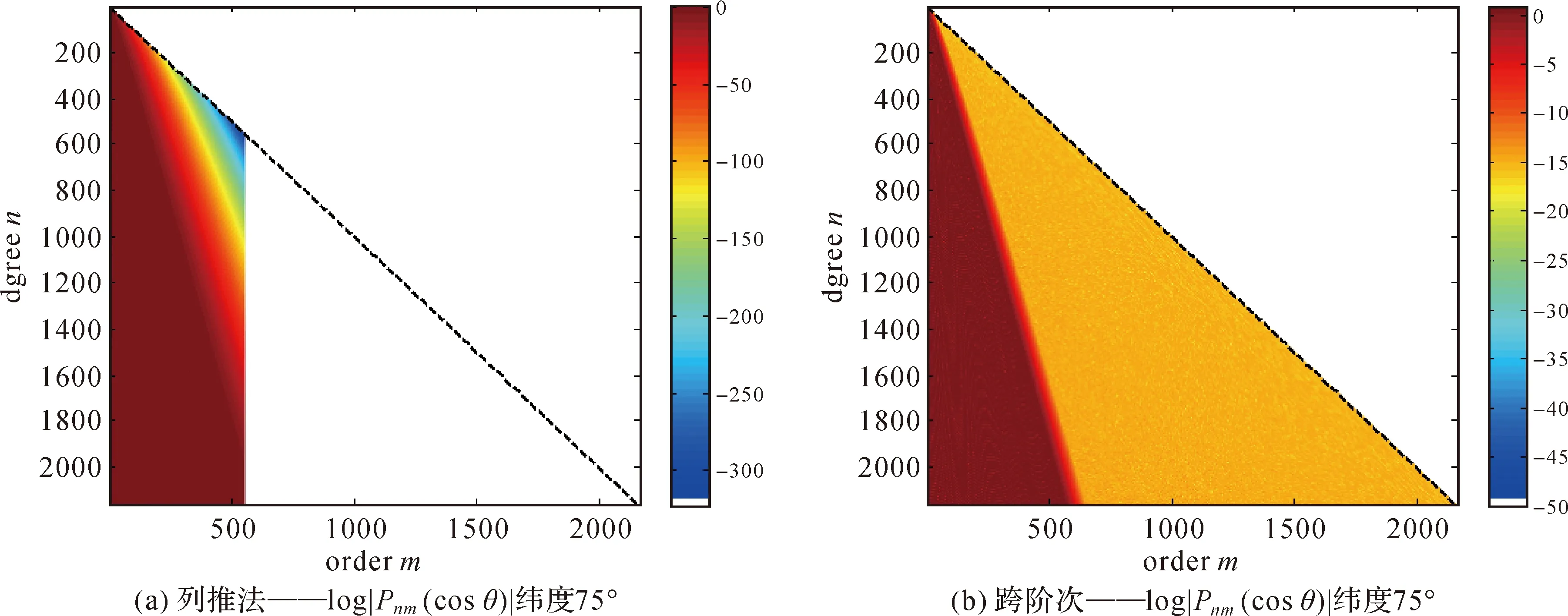
图2 标准向前列推法及跨阶次发方法的溢出情况比较[3]Fig.2 Comparison of overflow between standard forward method and cross order method

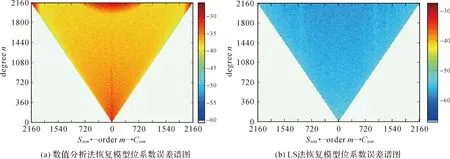
图3 模型恢复误差的比较Fig.3 Comparison on error of recovered model

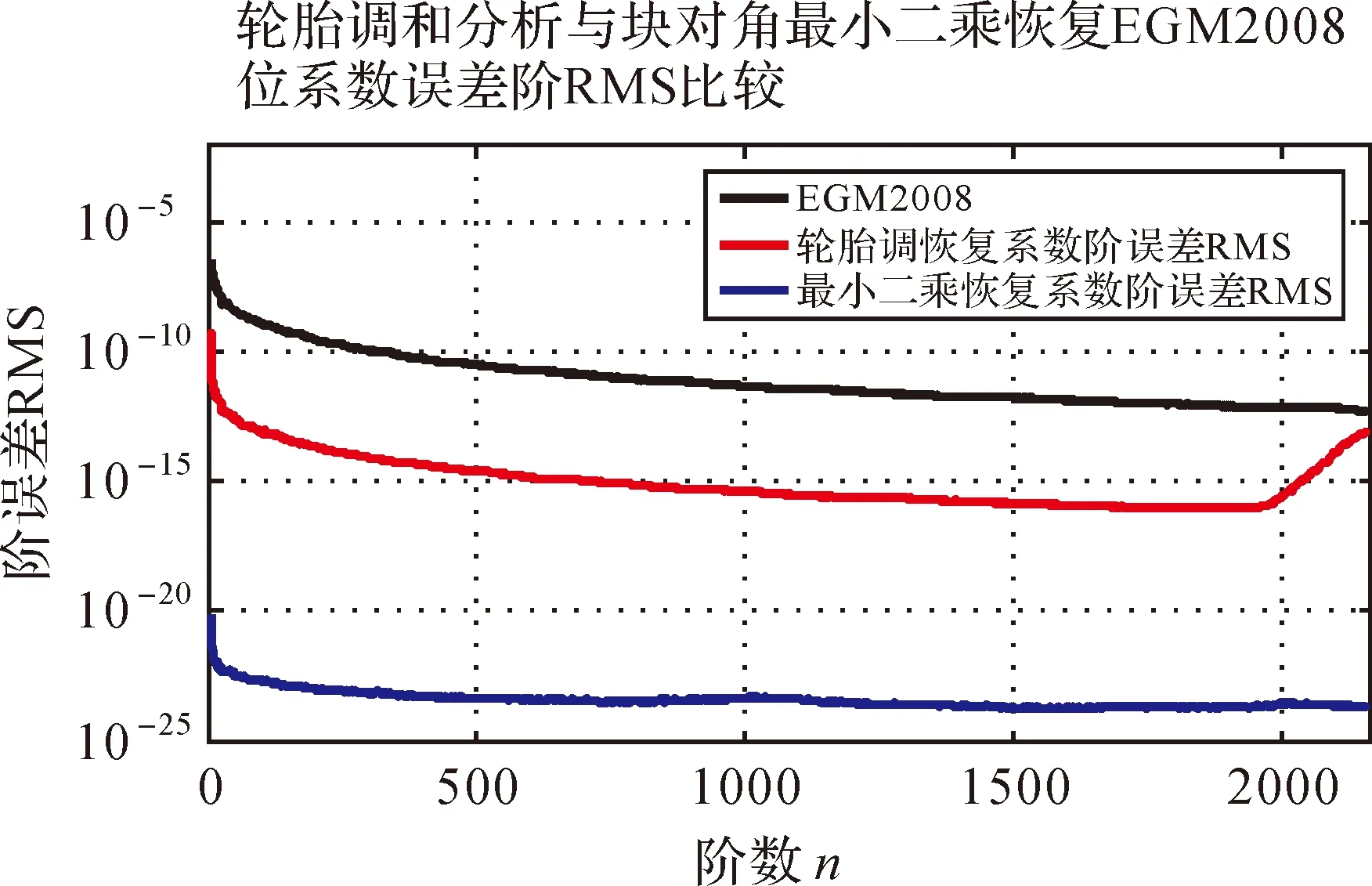
图4 误差阶RMS比较Fig.4 Comparison of error degree RMS

本文基于Pavlis提出的块对角最小二乘方法，通过对法矩阵求解方程进行约化、对Legendre函数的计算和存储方式进行设计，结合缔合Legendre函数关于赤道的对称性，解决了大型矩阵存储及计算效率低下的难题，实现了超高阶重力场模型最小二乘方法的小存储、高效率的解算。结果显示，精度相比数值积分方法提高近5个量级，计算效率提高近300倍，并精确估计了重力异常数据的精度。

本文最小二乘改进方法的局限性：采用上述高效的超高阶模型位系数最小二乘方法，在式(8)中，有权矩阵P为单位权阵这一假设。对其进行拓展，当位于同一经度的格网重力异常精度相同，或位于同一纬度的格网重力异常精度相同，这两种情况下也可以使用上述改进的快速方法。当出现每一片区域都有自己不同的精度这一情况下，上述方法是不适用的，这也是该改进方法最大的局限性。