一种INS辅助的PPP周跳探测方法
2018-11-30黎蕾蕾丁学文陈渠森柳景斌孙红星
黎蕾蕾,杨 盛,丁学文,陈 华,陈渠森,柳景斌,孙红星
1. 重庆大学航空航天学院,重庆 400044; 2. 重庆大学光电技术与系统教育部重点实验室,重庆 400044; 3. 武汉大学测绘遥感信息工程国家重点实验室,湖北 武汉 430079; 4. 中国兵器工业集团北方信息控制研究院集团有限公司,江苏 南京 211153; 5. 武汉大学测绘学院,湖北 武汉 430079
自20世纪末文献[1]首次提出精密单点定位技术(precise point positioning,PPP),PPP技术便成为GNSS领域中的一大研究热点。PPP技术无需地面基准站,具有更大的作业覆盖范围,可直接获得国际地球参考框架(ITRF)下的高精度测站坐标,是继RTK和网络RTK技术后出现的又一次技术革命。但在实际运用中,PPP往往会因障碍物的遮挡、接收机的运动、到达接收机处卫星信号的信噪比低、接收机或卫星的故障等原因而发生周跳[2]。若连续跟踪卫星少于5颗,则PPP在定位处理中需要数十分钟才能重新收敛到分米至厘米级定位精度[3]。因此,精确地探测与修复周跳有利于提高PPP重收敛速度,是PPP实际工程应用中的关键技术问题。
近年来,国内外不少学者针对周跳探测与识别问题提出了很多解决方案。这些方案能被归纳为以下4类:非差模型、双差模型、三频模型及外部器件辅助模型[4]。由于双差模型[5]主要针对DGPS,不适用于PPP;三频模型[6-8]以传输三频信号的卫星和接收三频信号的接收机为条件,并非现今工程运用中的主流;因此,非差模型和外部器件辅助模型成为国内外不少学者解决PPP周跳探测与修复的切入点。
在非差模型方面,文献[9]提出的TurboEdit方法首次融合了GF组合和MW组合去探测和修复周跳,并成功运用于GIPSY[10]、Bernese[11]等商业软件中;之后,文献[12—13]针对电离层快速变化的情况,提出了改进的TurboEdit方法。此外,文献[14]针对历元间差分模型,将周跳量引入方程作为参数估计,以实现实时PPP周跳瞬时校正;文献[15]通过预报的电离层延迟信息以实现PPP宽巷模糊度的快速固定;文献[16]运用MW组合和GF组合,提出了一种适用于实时PPP周跳探测与修复的策略;文献[17]则通过预测电离层延迟变化,提出了WL-L3-LX分级方法处理周跳。文献[18—19]将相对伪距而言精度较高的多普勒观测值用于周跳探测。以上这些方法,大都结合了MW组合。MW组合通过使用伪距和载波相位观测值,能有效探测出大周跳,但由于码伪距噪声及多路径误差的影响而不能有效探测出小周跳。
在外部器件辅助模型方面,借鉴于DGPS/INS组合中惯导信息被用于辅助GPS信号周跳探测与修复的思路[20-22],INS辅助PPP探测周跳成为了近几年一些学者的研究热点。其中,文献[23]首次发现,利用INS辅助PPP的宽巷与超宽巷相位组合,可实现周跳的探测与识别;文献[24]基于PPP/INS紧密组合模型,运用INS辅助PPP的无电离层组合与电离层残差组合联合求解,以实现周跳的探测与修复;文献[25]也运用INS辅助PPP去加快模糊度的收敛过程。
本文以PPP/INS组合为基础,利用INS短时高精度的位置信息,取代传统MW方法中伪距观测量,消除周跳探测中的几何位置关系,并通过星间差、相邻历元差、电离层延迟变化模型等方法,建立起INS辅助PPP的宽巷探测模型;通过与无几何距离(GF)组合方法相结合,实现对PPP双频等周周跳和特殊周跳(5/4、9/7等)的高精度探测。为了简化,本文所采用的双频组合为f1/f2,本方法也适用于f1/f3和f2/f3双频组合观测值的周跳探测。
1 PPP/INS组合模型
对于PPP原始相位观测方程,当使用精密星历和精密钟差产品消除其卫星轨道误差和卫星钟差,并将其他系统误差如天线相位中心偏差、相位缠绕、相对论效应、固体潮、大洋负荷改正,以及地球自转等,采用模型改正后,相位观测方程可以写为
(1)

在实际定位计算中,人们往往采用双频无电离层组合模型。该模型消除了电离层延迟低阶项,将接收机三维坐标、接收机钟差、对流层延迟和无电离层组合模糊度作为待估参数,并视相位小数偏差由模糊度吸收。无电离层组合模型可表示为
LIF=ρ+cdtr+T+λIFNIF+ε(LIF)
(2)
式中,下标IF表示无电离层组合。
PPP与INS紧密组合,由一个主滤波器对来自GPS接收机的原始测量数据和由INS估算的导航解进行融合。INS运用陀螺和加表测量数据进行捷联惯导计算,得到位置、速度、姿态等导航估算值,并结合精密星历与钟差产品,预测GPS伪距、载波和多普勒观测量;GPS利用误差模型与精密星历、钟差产品,校正伪距、载波和多普勒原始观测量,并将校正量与INS预测观测量之差作为卡尔曼滤波器的输入;经卡尔曼滤波融合处理,得到组合系统的误差状态估计并反馈至INS,一方面校正INS导航解并输出组合系统导航信息,另一方面补偿惯导传感器误差;此外,INS定位估算值也被用于辅助PPP进行周跳探测与修复,以增强组合系统的质量控制,如图1所示。综合考虑系统性能和可观测性因素,建立包括15维INS误差状态和GPS误差状态的状态向量

(3)
式中,误差状态按顺序分别为INS位置误差、INS速度误差、INS失准角、加速度计零偏、陀螺零偏、接收机钟差、钟差变化率、天顶对流层湿延迟及无电离层组合模糊度。滤波器观测量则为INS估计的相位、伪距、多普勒与GPS观测值之差
(4)
需要注意的是,伪距观测误差较大,因此只在初始化阶段使用。
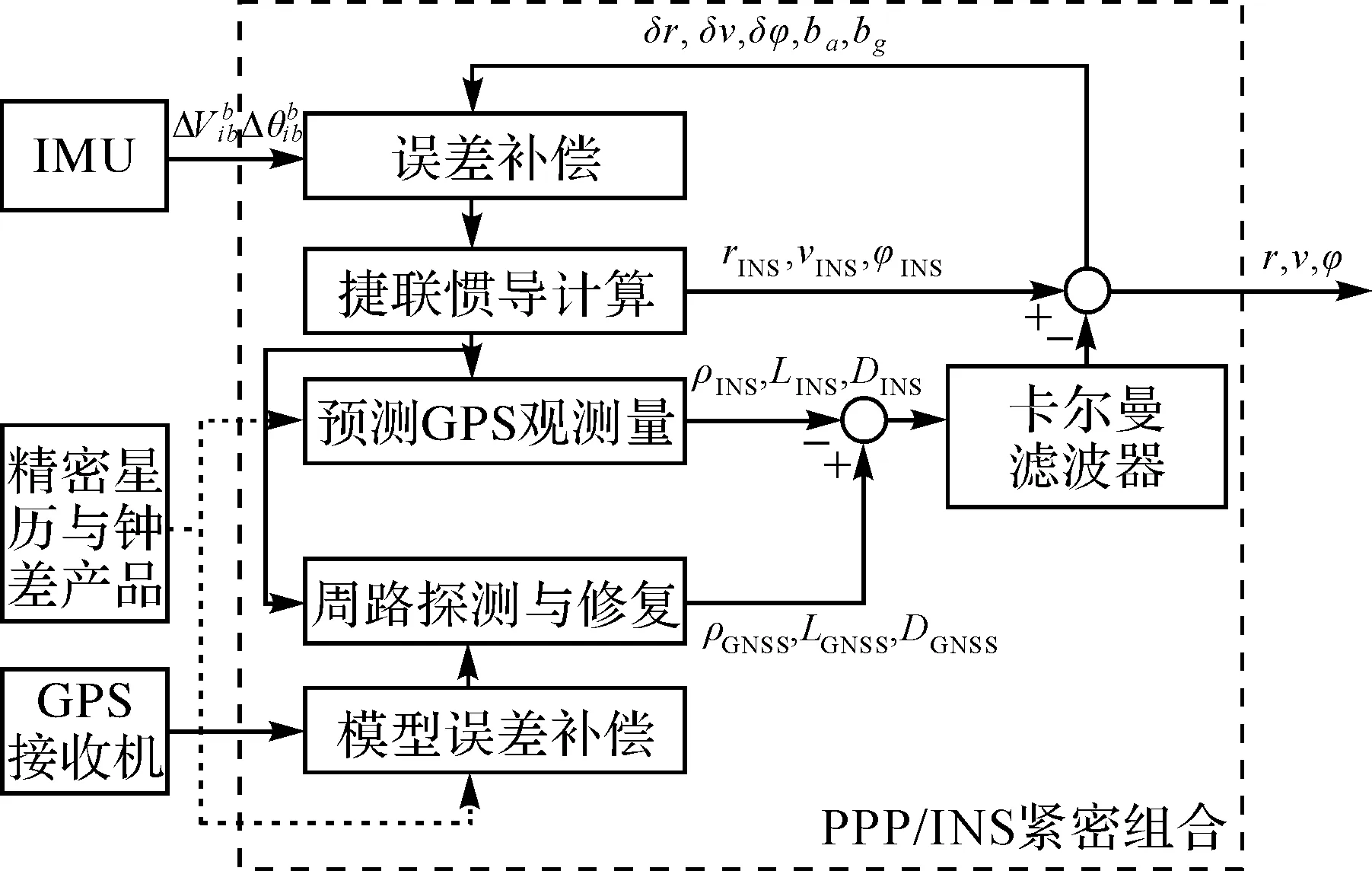
图1 PPP/INS紧密组合模型框图Fig.1 Architecture of cascade SINS/GPS deeply integrated system
2 周跳探测模型
2.1 INS辅助PPP的宽巷探测模型
利用宽巷易于探测的特点,本文运用INS辅助PPP进行宽巷周跳探测(WL-INS)。其基本原理为:利用INS和精密星历提供的接收机与卫星高精度位置信息,消除宽巷中的站星几何位置关系;通过星间差和历元间差分别消除接收机钟差、对流层延迟误差、电离层延迟误差和模糊度等参数,形成仅包含周跳参数且具有较高精度的检测量。由式(1),宽巷组合测量方程可写为
LWL=ρ+cdtr+T-IWL+λWLNWL+
(5)
式中,下标WL表示宽巷组合。
首先,利用INS定位结果和IGS精密星历,估计星站几何位置ρINS,建立包括INS位置信息的宽巷组合观测量LWL-INS
LWL-INS=LWL-ρINS-εINS=cdtr+T-IWL+
ε(LWL)-εINS
(6)
其次,选择合适的参考卫星进行星间差分,消除接收机钟差和接收机端宽巷相位小数偏差
ΔLWL-INS=ΔT-ΔIWL+λWLΔNWL+
(7)
式中,Δ表示星间差。
最后,对连续的历元观测量作历元差分,消除模糊度。由于24 h内卫星端宽巷相位小数偏差非常稳定[26],故历元间差分便将卫星端宽巷相位小数偏差消除;对流层延迟干分量采用模型估计,湿分量固定为PPP最新估计结果,由于短期内对流层延迟具有较强的时间相关性[15],因此对流层延迟残差可以被忽略。影响周跳探测的一个重要因素是未模型化的电离层延迟,当电离层中的电离子含量平滑变化时,历元间差分可以消除电离层延迟[15];但当电离层变化较快及GPS信号长时间中断的情况时,历元间差分便无法消除电离层延迟,此时采用相对电离层模型的方法,将短时间内电离层延迟近似成线性变化[27],在无周跳或周跳修复成功的条件下,通过电离层残差组合获取滑动窗口内电离层变化δIi,进而预报当前历元时刻的电离层信息。由此可得双差相位宽巷组合观测方程
δΔLWL-INS=λWLδΔNWL+δΔε(LWL)-δΔεINS
(8)
δΔNWL=δΔN1-δΔN2
(9)
式中,δ表示历元间差;δΔNWL为宽巷周跳;δΔε(LWL)为双差相位宽巷误差;δΔεINS为双差后的INS误差;δΔLWL-INS即为周跳探测的检测量DVWL-INS(decision variable,DV)。
2.2 无几何距离组合探测模型
根据式(1)可得无几何距离组合(phase geometry free,GF组合)的载波相位观测值LGF
LGF=L1-L2=λ1N1-λ2N2-(I1-I2)+ε(LLG)
(10)
将前后两历元GF组合的载波相位观测值作差
δLGF=λ1δN1-λ2δN2-δ(I1-I2)+δε(LLG)
(11)


ε(LGF_est)
(12)
式中,δLGF即为检测量DVGF。
3 精度分析
3.1 WL-INS探测模型精度分析
假定所有误差满足高斯分布,由误差传播律可得
(13)
式中,σWL-INS表示INS辅助宽巷周跳检测量中误差;σINS表示惯导中误差;σLWL表示相位宽巷组合中误差
(14)
式中,f表示载波频率;σ表示载波相位观测值误差。
为实现单历元对最小1周的周跳探测,INS辅助宽巷周跳探测阈值TWL-INS应为宽巷波长的一半,本文取0.5 m作为WL-INS周跳探测阈值。当检测量DVWL-INS大于周跳探测阈值时,即认为此时发生了周跳。以3倍中误差为标准,INS辅助宽巷周跳检测量中误差应满足
3·σWL-INS≤TWL-INS
(15)
结合式(13)和式(14),可知惯导中误差σINS≤0.082 3 m。即当惯导单独定位精度在0.08 m以内时,惯导可有效辅助PPP宽巷周跳探测。
根据惯导误差传播方程[28-29],惯导独立导航期间位置中误差为
(16)
式中,σg为陀螺引起的位置中误差;σa为加速度计引起的位置中误差;g表示重力加速度;bg表示陀螺零偏;ba表示加速度计零偏;t为惯导独立导航时长。
以典型战术级IMU(陀螺零偏0.3(°)/h,加速度计零偏100 μg)为例,0.1 s、1 s和10 s独立导航时间内,惯导位置误差分别为5×10-6m、5×10-4m和0.05 m,完全满足WL-INS周跳探测模型对惯导精度要求,且在短时间内,惯导误差远小于相位宽巷误差。因此,INS辅助PPP宽巷模型对周跳非常敏感,它不仅可以探测出小周跳,而且能在短时间内恢复很高精度的整数周跳,从而实现PPP快速重新初始化。但由于INS辅助PPP的宽巷探测周跳方法无法确定各个频率上的周跳,也无法探测双频等周周跳,因此本文将其与探测精度较高的GF组合方法相结合。
3.2 GF组合探测模型精度分析
由误差传播律,GF组合载波相位观测值中误差为
(17)
考虑到受残余大气层延迟误差、多路径误差和电离层模型误差等影响[19],一般取σGF=0.01~0.02 m。以3倍中误差为标准,取GF组合周跳检测量阈值TGF为0.05 m。当检测量DVGF大于周跳探测阈值时,即认为此时发生了周跳。
4 试验测试与分析
本文试验采用的跑车数据采集于2013年7月2日,地点为北京郊外一段空旷地区,卫星观测条件较好,主要设备包括基站、流动站GNSS测地级接收机,以及某型国产光纤IMU。基站和流动站接收机采样率均为10 Hz,IMU采样率为200 Hz,陀螺零偏0.3°/h,加速度计零偏100 μg,总数据时长约为1.5 h,跑车平面轨迹如图2所示。本文使用流动站GPS和IMU数据实施PPP/INS组合及周跳探测试验;使用基站数据作双差处理(星间差、站间差),固定流动站L1、L2模糊度,获得对应的宽巷周跳并作为INS辅助PPP周跳探测参考值。在整个测量过程中,PRN03号卫星仰角均在70°以上,且未发生周跳,故被选作为参考卫星。

图2 跑车平面轨迹Fig.2 Plane trajectory of the car
4.1 模拟周跳试验
MW组合、WL-INS组合和GF组合检测量DV及其统计量分别如图3和表1所示。其中MW组合由于引入了观测误差较大的测距码观测量,其探测精度较低,周跳检测量数值范围达±100 cm,标准差为15.3 cm;INS辅助宽巷组合采用了较测距码精度要高INS位置信息,其检测量精度得到大幅度提高,基本在±2 cm以内,检测量标准差为0.61 cm;GF组合由于仅使用相位观测量,其探测精度最高,基本保持在±0.2 cm以内。在整个测试周期内,PRN23号卫星的周跳检测量均未发现明显变化,表明该颗卫星没有发生周跳。

图3 PRN23号卫星各组合检测量变化Fig.3 DVs for PRN23
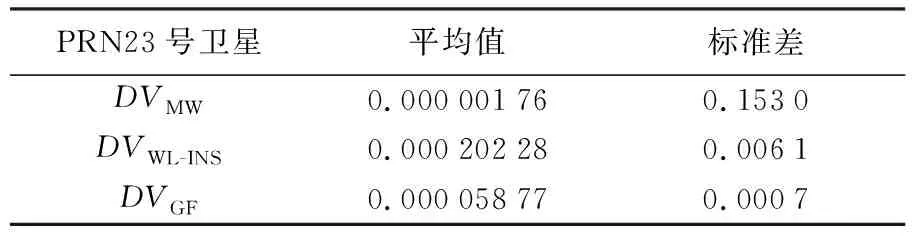
表1 PRN23号卫星各组合检测量的统计量
对上述PRN23号卫星人为引入等时间间隔(即200 s)的14组周跳,使用MW组合、WL-INS组合和GF组合方法分别进行周跳探测,模拟周跳数值及检测量变化分别如表2和图4所示。其中MW组合周跳检测量噪声为

式中,σP表示码误差噪声中误差。以3倍中误差为标准,MW组合周跳检测量阈值TMW取为1.5 m。由表2和图4可知:
(1) MW组合方法因采用了随机误差较大的码数据,对小周跳不太灵敏,宽巷小周跳(如0/1、3/4、5/4、5/6等)和双频等周周跳(如1/1、3/3等)淹没在系统噪声中,且部分检测量(如2/4、7/0等)的小数周部分数值过大,不利于后续修复周跳。

图4 加入模拟周跳后PRN23号卫星各检测量变化Fig.4 DVs for PRN23 with simulated cycle slips
(2) WL-INS组合方法探测精度较高,对宽巷小周跳非常敏感,且检测量的整数性明显较MW组合要好,有利于后续修复周跳以及快速恢复模糊度,但WL-INS方法无法探测双频等周周跳(如1/1、3/3等)。
(3) GF组合方法探测精度较高,能探测出绝大多数大小周跳以及双频等周周跳,但对于特殊组合周跳(如5/4、9/7等)则无法有效探测。
因此,综合WL-INS组合和GF组合方法,可以实现此两种方法的优势互补,进而成为一种探测精度高的周跳探测方法。

表2 PRN23号卫星模拟周跳探测结果
注:*号标记为未探测出周跳处。
4.2 实测周跳试验
以PRN07号卫星为例,图5为PRN07号卫星的MW组合、WL-INS和GF组合观测量的变化图。
从原始数据分析和图形变化可以发现:在测试期间,PRN07号卫星信号一共发生了8处数据中断(中断时长详见表3)。在卫星连续观测区间内,WL-INS组合和GF组合观测量连续变化且波动较小,但因受电离层等延迟影响,出现趋势化漂移现象;相比之下,MW组合观测量无漂移现象,但受码随机误差影响,数值波动比较大;当信号中断并重新捕获后,MW组合、WL-INS组合和GF组合观测量均发生跳变,但WL-INS组合和GF组合观测量在跳变后仍然保持平稳,而MW组合观测量则出现明显的“毛刺”现象,说明接收机在重新捕获信号后短时间内有明显观测偏差。

图5 PRN07号卫星各组合观测值变化图Fig.5 Observed values for PRN07
图6为MW组合、WL-INS组合与GF组合3种周跳检测量随时间的变化。表3则给出了各检测量数值、相应宽巷周跳数,以及宽巷周跳参考值。由于实际发生的周跳较大,上述方法均能有效探测出周跳。将WL-INS与MW组合方法所探测出的宽巷周跳数与宽巷周跳参考值作对比,可以发现:
(1) MW组合方法未能成功求解所有实际周跳,这是由于当接收机信号中断并重新捕获后,短期内码观测误差较大,需要经过一段时间收敛到稳定状态,导致MW观测量出现如图5(a)所示“毛刺”现象。此时若运用MW方法进行处理,它将无法避免“毛刺”的影响,求解周跳错误。

图6 PRN07号卫星的各组合检测量Fig.6 DVs for PRN07
(2) WL-INS组合方法不受初始捕获阶段较大观测误差的影响,对所有的实际周跳均能成功求解出,且取整精度较高。
需要说明的是,在运用双差方法固定模糊度的过程中,193 887.6 s与193 893.6 s两个历元时刻PRN07号卫星均发生周跳。由于时间间隔短,导致前者模糊度无法被固定,而后者模糊度实现了固定,此时检测出193 893.6 s的宽巷周跳为两者周跳之和。此外, 本文中所采用的陀螺零偏为0.3(°)/h,加速度计零偏为100 μg,由式(16)可得,惯导辅助PPP周跳探测的有效时间约为13 s。
5 结 论
本文针对PPP/INS组合中载波相位周跳探测问题,提出了一种INS辅助PPP周跳探测的新策略。将INS高精度位置信息引入到宽巷组合中,消除其中的站星几何位置关系,并综合运用星间差分、历元间差分的方法,实现INS辅助的宽巷组合周跳探测方法。通过模拟周跳与实测数据表明,WL-INS方法克服了传统MW方法受码误差、多路径等因素影响的不足,能识别各种宽巷小周跳;针对WL-INS方法无法探测等周周跳的问题,提出综合运用GF组合和WL-INS组合方法,弥补各自的探测盲点,实现高精度周跳探测的目的。此外,WL-INS方法仅利用周跳前后两个历元的观测值进行处理,可实现实时单历元周跳探测。

表3 PRN07号卫星实际周跳探测结果
惯导累积误差是影响WL-INS方法探测精度的主要因素之一,在PPP连续定位条件下,即使部分卫星出现信号中断,惯导受GPS连续校正,惯导累积误差影响可以被忽略;在GPS信号全部中断条件下,惯导单独进行定位,其误差会随时间显著增加,导致WL-INS方法探测精度降低,但由于宽巷波长比较长,在惯导辅助PPP周跳探测的有效时间内,WL-INS辅助周跳方法仍然有效。
