阶梯流作用下长柔立管涡激振动行波效应研究

2018-11-30乐智斌

船舶力学 2018年11期

白旭，乐智斌

（江苏科技大学船舶与海洋工程学院，江苏镇江212003）

0 引言

深水立管是连接海底井口与海面作业平台的关键设备。在复杂的海洋环境中，由海流引起的涡激振动（VIV）是造成立管发生疲劳破坏的主要因素[1]。

由于深水立管具有大长细比等特点，其涡激振动响应呈现出非线性特征，与刚性圆柱体存在较大差异。Bourguet等[2]通过水池试验发现长柔结构物发生涡激振动时在顺流向存在十分显著的响应，并指出在高质量比下单自由度和双自由度涡激振动差距较小，而低质量比条件下顺流向的振动被激发无法忽略。因此可以认为在低质量比条件下对海洋长柔立管进行涡激振动响应分析时，必须考虑顺流向的影响。对此，唐国强等[3]进行了长细比为1750的柔性杆件涡激振动实验，发现顺流向的振动频率和振动模态数均为横向的2倍。Gao等[4]通过实验对比剪切流和均匀流作用下加设了抑制振动装置的立管，发现在均匀流时立管会产生比剪切流下更高的振动频率。林琳等[5]通过莫里森方程计算顺流力，建立了三维柔性立管的双自由度涡激动力响应方程，发现剪切流作用下随着流速的增加，立管模态数逐渐增加。郭海燕等[6]利用功能原理建立了立管涡激振动响应数值模型，采用Newmark-β方法在时域内迭代求解其动力响应，并与实验进行对比后得到一种能够预测大长细比海洋立管涡激振动模态和振幅极值点的计算模型。Wang等[7]同样发现了剪切流作用下立管的模态数与流速之间的关系，也发现剪切流的振动频率小于均匀流，并指出在顺流向会出现3倍于横向的振动频率。宋磊健等[8]、高云等[9]通过进行三维立管模型的实验发现在剪切流下，其阻力系数等也与均匀流存在较大差异，在剪切流下横向振动存在一个频率锁定区域，而顺流向则存在两个频率锁定区域，且响应随着约化速度出现上升—下降—再上升—再下降的趋势。

行波效应是振动响应在空间和时间上同时发生变化的振动现象，针对立管的行波效应现象，国内外学者通过柔性立管涡激振动实验进行了大量分析。Chaplin等[10]在实验室条件下进行了阶梯状来流，均匀流和线性剪切流的海洋立管涡激振动实验，实验中均发现了显著的顺流向振动，尽管数据显示顺流向振动的幅值相对横向较小，但是其激发了更高阶的模态，行波效应明显。Jaiswal[11]在墨西哥湾进行的实验测量以实时的流速模拟剪切流对立管的影响，发现行波效应，并总结得到行波效应从高约化速度区域向低约化速度区域传播的结论。Bourguet等[12]对线性剪切流进行了大量的数值计算，发现剪切流和均匀流作用下，具有行波效应的区域与其他区域有着不同的运动轨迹，通过对相位的分析，发现在频率锁定区域相位均小于180°。罗冬冬等[13]通过CFD计算剪切流作用下的柔性隔水管发现最大位移所在位置会发生向上移动的现象，同样也说明了行波效应的存在。

长柔立管的涡激振动在发生高模态振动情况下会出现行波效应，即结构的振动响应幅值随着轴向会出现一个有规律的波动，特别是在考虑顺流向振动时，发生的振动频率变得更高，所激发的模态也变得更高，行波效应变得更为明显。对于行波效应而言，其结构振动响应特性和导致的疲劳分布规律与驻波效应有明显的区别。传统的涡激振动预报方法对于驻波效应有效，而对于行波效应占主导的高模态数长细柔弹性体涡激振动，模态叠加法只能对有限数量的非共振模态进行分析和计算，无法体现长柔立管在考虑顺流向振动的双自由度涡激振动响应特性。由于频域预报模型在预报大长径比长柔立管时会受到行波效应的影响，采用时域预报模型会更有优势，同时也为了更好地研究涡激振动中的流体作用力，大量国内外学者通过建立力分解模型和尾流振子模型得到一系列预报模型。2004年，Facchinetti[14]提出的单自由度涡激振动耦合振子模型能够很好地模拟涡激振动运动响应，充分研究了结构和流体振子的耦合作用，分别对位移、速度、加速度三种耦合形式进行了对比和讨论，该方法引起大量学者的研究和补充。Bai等[15]通过将尾流振子模型扩展到双自由度形式，研究了该模型在双自由度即顺流向和顺流向发生运动时的相位角和轨迹的关系。

时域预报模型能够更好地对深水海洋立管的涡激振动进行预报，由于长柔立管在涡激振动时因行波效应会引起疲劳点的转移，在进行运动响应预报和疲劳寿命计算时时域预报模型具有更大的优势。而尾流振子模型更好地诠释了双向流固耦合的内涵，属于一种最适合用以描述涡激振动这一类典型的自激振动。因此采用尾流振子模型进行时域预报模型的建立以分析深海长柔立管的涡激振动现象具有重要的工程价值和研究意义。因此本文以离散点涡法为基础，建立三维的尾流振子计算时域模型，分析获得阶梯流作用下长柔立管的涡激振动响应特征参数，探索阶梯流作用下长柔立管涡激振动行波效应机理。

1 长柔立管涡激振动模型

1.1 三维柔性立管双自由度耦合方程

海洋立管长径比通常大于一百，甚至有些达到千量级，故将立管看成具有柔性能够发生变形的长细柔性杆处理，建立三维立管涡激振动物理模型如图1所示。

除受到作用在截面的来流外，立管结构还受到尾涡引起的顺流向和横向的涡致作用力，因此可以将立管力学问题整体简化为长细柔性梁的复杂弯曲问题。以横向的振动为例，取立管沿高度方向的一个微段dz，如图2进行分析。

通过力矩平衡方程和变形几何关系可以得到如下表达式：

其中：M为梁端面的弯矩，E为立管材料的弹性模量，I为立管的截面惯性矩，Fs为截面剪切力，Y为微段的横向振幅。 F （ y，z，）t为流体作用力，假定每一微段为刚性体（自身不发生形变），两端弹性支撑，可得到物理模型如图3所示。

根据文献[15]，可以得到尾流振子模型的双向流体作用力表达式：

其中：D为圆柱直径；fst为系统泻涡频率；α为与脉动拖曳力、斯特拉哈尔数、脉动升力系数相关的无量纲参数。

考虑到立管在轴向受到拉力作用，依据轴向的平衡方程，结合d2Y/dz2=M/EI可以得到：

扩展到顺流向，结合公式（1）、（2）和（3）并无量纲化，得到基于欧拉—伯努利梁假定成立的长柔立管双自由度涡激振动方程：

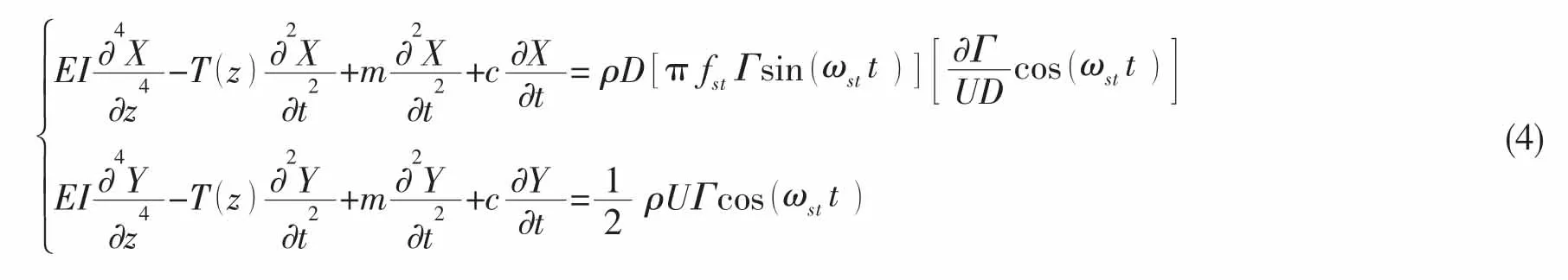
假设随着水深的增加，立管截面、质量和阻尼均没有变化，但轴向拉力需要考虑自身的重力作用。当立管所在流域不是均匀来流而是随着水深变化存在有阶梯的水流时，等式右边的载荷也随之变化。

根据文献[16]，结构在流体通过时的振动可以用离散分布的非线性范德波尔振子模型来描述：

其中：ε是范德波尔方程耦合参数，vd是耗散参数，Fd是流体作用在结构上的载荷项即流固耦合作用力，ωst=2πStU/D是流体泻涡频率，与流速以及斯特劳哈尔数有关。对于耗散项vd∂3q/（∂z2∂）t，当结构整体进行离散化处理时，只要沿着轴向划分足够多节点，可以认为单个单元的∂2q/∂z2=0。因此三维流体振子方程可以表达为：

假设结构的截面沿着轴向均是相同的形状与大小，截面惯性矩不随轴向发生变化，立管截面惯性矩取I；由于立管轴向拉力随着水深而变化，T（）z为沿着轴向分布的轴向拉力。综合以上讨论，结合（4）式和（6）式可以得到三维双自由度长柔立管涡激振动耦合模型如（7）式，式中N、M和H均为水动力参数[15]。

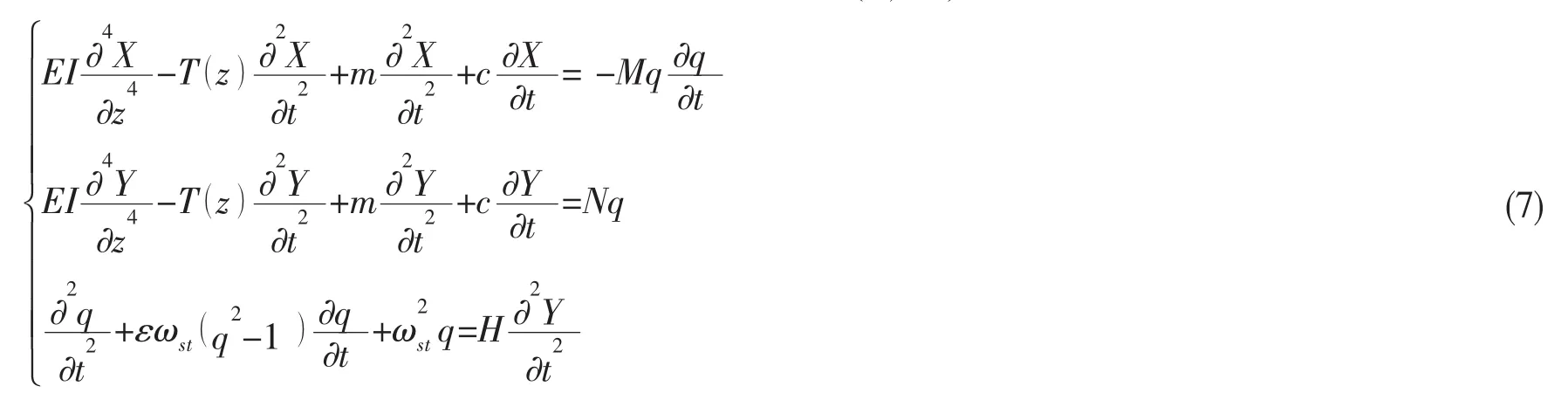
1.2 模型验证

针对海洋环境中真实存在的阶梯流，Chaplin进行了经典的阶梯流实验，将一根13.12 m的圆柱立管放置于套管中随拖车运动，由于套管中水静止，以此模拟海洋中洋流发生阶梯性变化的实际工况[10]。该实验所用模型参数如表1所示。

表1 Chaplin试验参数Tab.1 Test parameters of Chaplin

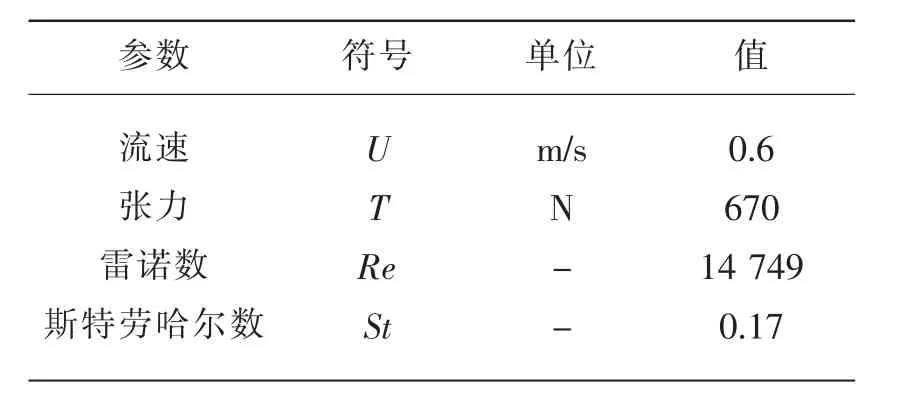
表2 验证工况Tab.2 Verification condition

为验证（7）式的正确性，选取Chaplin一组工况进行对比验证，所选工况参数如表2所示。最大流速为0.6 m/s，立管下方45%部分受到流速影响，其他部分为静水作用，仅受到湿重影响，由于结构总长为13.12 m，对0～5.9 m段施加水流进行计算。

得到载荷与实验结果对比如图4所示，依次为横向振幅的包络线对比图、横向振幅的标准方差对比图和顺流向振幅标准方差对比图。结果表明：在流速为0.6 m/s下，该立管出现6阶模态。沿立管高度方向振幅一致，对比立管上方的振幅，本文模型较实验结果略大是因为在实验中边界进行铰接，仍然存在一定的阻尼；另一方面，套管内径较小，与下方置于水池的流域相比，对立管振动具有更大的阻碍，因此立管上部分的实验结果较下部分更小，同时也小于模型结果。两个自由度的振幅标准方差结果对比也基本一致，实验和模型计算结果在同样的位置出现，横向振动被激发6阶模态，顺流向被激发11阶模态，顺流向模态数大致为横向的2倍。通过对比Chaplin的实验结果与（7）式的计算结果，本文提出的计算模型和方法能够有效地对立管在阶梯流下的运动响应进行预报。

2 阶梯流作用下长柔立管涡激振动响应特性

不同的海洋环境中，存在多种来流形式，根据成因可以分为潮流、风海流、阶梯流、热盐环流和波浪流等，随时间变化可以分为周期流、定常流和瞬时流等。由于海洋环境复杂，立管的工作条件恶劣，会出现大量的未知载荷。而立管在不同的流动形式下振动响应存在着巨大的差异，本文针对阶梯流，采用提出的模型对长柔立管进行涡激振动特性分析。

2.1 长柔立管涡激振动的振幅分析

设定流速U范围为0.2～5 m/s，雷诺数范围为2458～12290。模型总长13.12 m，进行200等分，共得到201个节点，流动形式如图5所示，具体工况参数见表3。

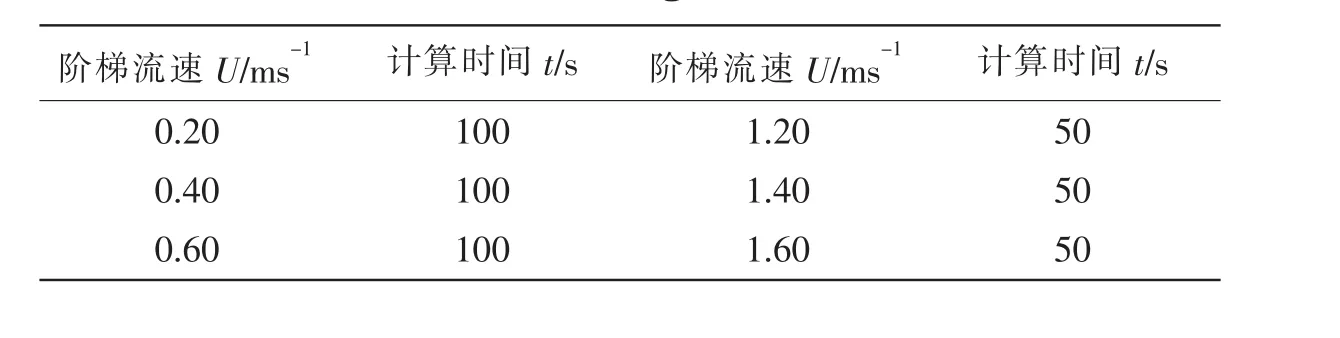
表3 阶梯流计算工况Tab.3 Working condition

模型计算得到所有工况下的响应后，为了说明该程序在时域上计算的稳定性和可行性。针对阶梯流在低流速U=0.2 m/s下，选取L/4，L/2，3L/4处的计算结果绘制双向无量纲振幅时程曲线，如图6所示。可以发现：在阶梯流作用下，无量纲横向振幅最大值发生在L/4处，为1.04。

续表3

绘制阶梯流在流速U=0.2 m/s下稳定后的截面运动轨迹，如图7所示。从图中可以看出：阶梯来流作用下，横向振幅的截面形状不存在节点，激发2阶模态，顺流向振幅的截面形状存在1个节点，激发3阶模态。

2.2 长柔立管涡激振动频率分析

长柔立管的寿命除了受到振幅的影响外，发生长时间的高频率振动也是其疲劳破坏的重要因素之一。对于二维刚性圆柱的振动，大量学者通过实验得到顺流向振动频率为横向振动频率的2倍。对于长柔立管而言，振幅较刚性圆柱更大，因此其振动频率的研究更为重要。

通过傅里叶变换对表3中所有工况的计算结果进行频率分析，选取L/4、L/2和3L/4处随时间变化的振幅进行分析得到如图8所示的无量纲幅频曲线。对比幅频曲线，可以看出，随着流速的增加，主频率增加。主频率随流速的变化趋势如图9所示。

横流向和顺流向振动的主频率与流速之间呈现出线性的关系，用fCF_main和fIL_main分别代表横向振动主频率和顺流向振动主频率，则可以得到fCF_main=5U及fIL_main=10U的表达式。以上分析均基于50号节点、100号节点和150节点的振动结果，为了更进一步研究立管上所有节点的振动频率与流速之间的关系，取低流速0.8 m/s以及高流速2 m/s进一步分析振动幅频图谱，如图10～11所示，可以看出亦满足上述的规律。

3 行波效应与传递特性

根据Jaiswal[11]发现的行波效应可以认为顺流向的高阶振频是引起行波效应的原因之一，为了更深入地研究不同流速下阶梯流行波效应在横向及顺流向上的传播规律，对表3中的0.2 m/s，0.4 m/s和2 m/s三种工况进行行波特性分析。从图12中可以发现随着流速的增加，会激发更高的模态数，横向振幅最大发生在0.4 m/s的阶梯流时。

文献[17]发现长柔立管在发生涡激振动时沿轴向变化的流体作用力波动区域即为频率锁定区域，同时该区域的相位稳定在180°以下，表现为运动轨迹为CC（counter clockwise）方向。文献[8]中给出了C模式（当横向运动达到最大值时，立管运动方向与来流方向相反，为顺时针）和CC模式（当横向运动达到最大值时，立管运动方向与来流方向相同，为逆时针），如图13所示。

当立管的横向运动达到最大值时，CC模式下立管在泻涡前朝来流方向运动。当泻涡时立管受旋涡影响运动回到中心点，因此其运动与最新的泻涡频率接近，产生频率锁定。因此在频率锁定区域一个典型特征为运动轨迹出现CC模式，可以以此判别频率锁定区域，也是能量输入区域。

为研究在不同流动形式下的能量输入区域分布规律，对0.2 m/s流速下阶梯流的运动轨迹进行深入分析，如图14所示。并在图中表明了CC模式为双向相位差小于180°的运动轨迹。

图15为阶梯流在0.2 m/s时的立管整体振幅随时间变化的变化图。对比图14和图15的各个工况进行以下分析：在阶梯流作用下，z/L为0.4～0.6范围出现CC模式的运动轨迹，对应地在图15（a）的横向振幅图上，0.3和0.7附近出现最大振幅，而顺流向振幅图同样在该区域出现了行波效应。

对比分析可以认为在运动轨迹出现CC模式的附近会出现行波效应，而横向振幅的最大值同样发生在该区域附近。而行波方向从振幅大的地方向振幅小的区域传播，即从能量输入（power-in）区域向能量输出（power-out）区域传播。

在阶梯流作用下行波效应和驻波效应非常明显，为了更好地描述驻波和行波之间的关系，分别选取了较高流速0.6 m/s和1.2 m/s的两种阶梯流进行分析。图16和图17分别为0.6 m/s和1.2 m/s阶梯流双向振幅随时间的变化图谱。驻波区域呈现稳定的振幅，沿立管轴向没有明显变化，而行波区域沿着立管轴向存在明显的位移变化。可以看出：横向以驻波为主，顺流向在边界和静止区域出现驻波，行波从阶梯流高流速区域向低流速区域传递。