深海采矿转臂关节运动规划的遗传退火算法
2018-11-30程一凡周知进
程一凡 杨 智 周知进
(1.湖南电气职业技术学院,湖南湘潭,411101;2.湘电集团,湖南湘潭,411101;3.贵州理工学院机械工程学院,贵州贵阳,550003)
目前的深海采矿采集系统不能应用于商业化开采的原因有经济性与技术性2个方面。其中技术性主要存在采集率低、海底的行走机构适应性差、对海底地貌破坏严重等问题[1-4]。采矿转臂可以调整关节的角度即调整采矿姿态,去适应海底不同的地形,这样采集率将大大提高[5-6]。
采矿转臂为了适应海底地形,要不断变化采矿姿态,且其位置的精度直接影响到集矿率。为准确快速控制采矿转臂的采矿姿态,文献[4]对转臂进行动力学建模并进行运动规划,但其规划中没有考虑水动力,且采用的普通遗传算法优化有不可避免的缺点。所以本研究采用Kane法考虑水动力建立转臂深海姿态调整时的动力学模型,并在此基础上采用遗传退火算法对转臂关节运动进行规划,使其变幅机构之间力矩变化幅度最小,从而运动平稳,姿态调整容易控制[7-8]。
1 采矿转臂动力学模型
转臂支腿式深海集矿机构[8-9]如图1所示。在对转臂的运动规划中,除了考虑各运动量的大小以及其连续性等问题,还要考虑其转臂的力矩,所以必须要建立转臂的动力学方程。
1.1 节臂等效受力

根据文献[9-12],节臂所受水动力可以等效为对节臂质点一个作用力与一个力矩的叠加,节臂之间变幅机构通过油缸的伸缩去驱动节臂,其等效于添加力矩M1,M2,M3,所以转臂受力如图2所示[4]。
M1,M2,M3均为驱动力矩;均为重力与浮力的等效合力;TP1,TP2,TP3均为集矿器对节臂的张力;Ff1,Ff2,Ff3均为水动力集中力;T1,T2,T3均为节臂水动力力矩;Ff为浮力轮对节臂的浮力。
1.2 Kane法转臂动力学模型
节臂的主动力(矩)方程为:
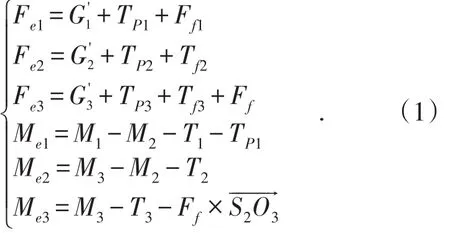
节臂的惯性力(矩)方程为:

其中,ac1、ac2、ac3分别节臂质心的加速度;I1,I2,I3为各节臂转动惯量;ε1、ε2、ε3分别是节臂的角加速度;m1、m2、m3分别为名节臂臂质量。
由kane法[13]可得广义主动力必须满足如下等式:

则转臂的广义动力分别为:
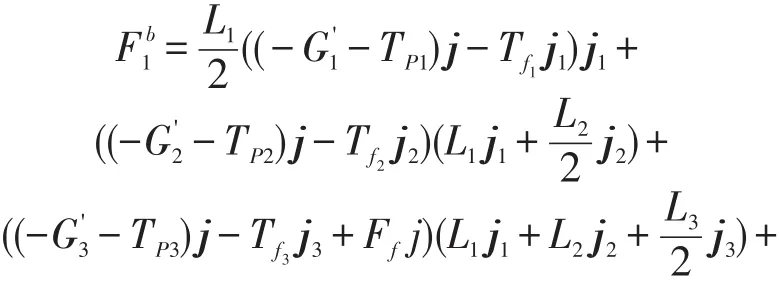
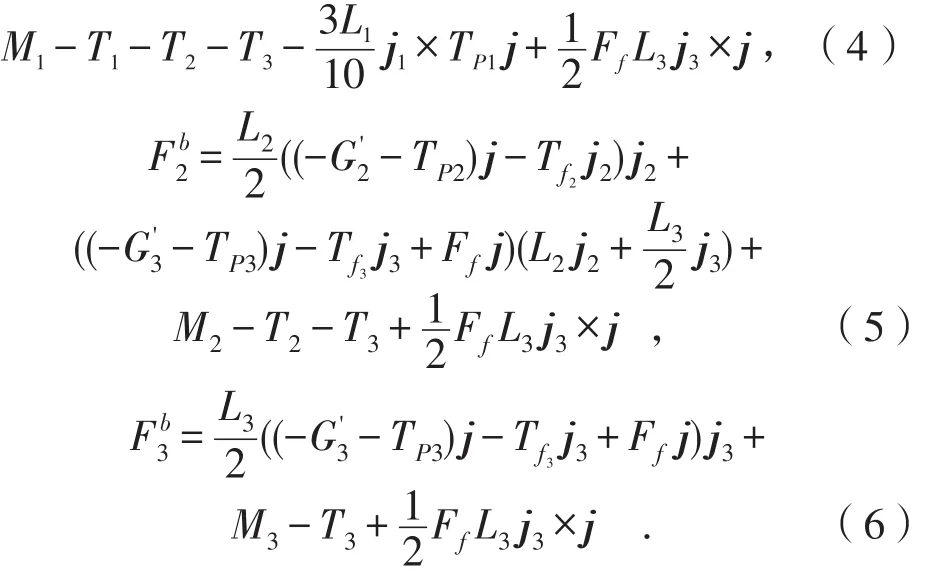
广义惯性力必须满足如下等式:
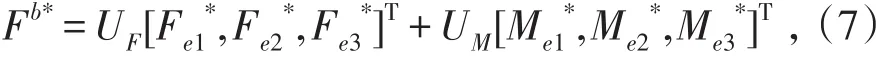
则广义惯性力分别为:
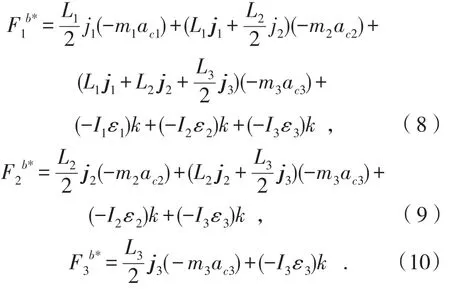
系统的主动力与惯性力必须平衡,则必须满足如下等式[8]:

联立以上等式就能建立系统的动力学方程,根据以上方程只要给出转臂的位置及速度就能求解出其驱动力矩[4]。
2 采矿转臂的关节运动规划
当采矿转臂关节的转速不同,其各变幅机构的驱动力矩将不同,而驱动力矩的波动直接影响到控制的精度,从而影响到采集率[4,7]。转臂的轨迹规划其实就是为了控制转臂从初始姿态转到目标姿态时,规划其路径并控制其速度、加速度。在对转臂的轨迹规划中,目前有2种方式[14-15]:笛卡尔空间轨迹规划与关节轨迹规划。笛卡尔空间运动轨迹规划,其建立的运算坐标为直角坐标,要根据目标末端点的轨迹曲线,并利用运动逆运算求解关节量。关节轨迹规划是直接控制关节的转速,并满足角速度、角加速等约束条件,选择不同的函数插值生成关节量与时间的函数。对应深海采矿转臂,其末端运动轨迹没有要求,但存在关节的逆运算计算量大、反应时间长等问题,所以不宜使用笛卡尔空间轨迹规划。关节空间轨迹规划需要给出初始姿态,终止姿态及运动时间。在对转臂的运动规划中,除了考虑角速度的连续性等问题,还要考虑其转臂的力矩,所以必须要根据动力学模型求解转臂的驱动力矩。
2.1 遗传退火算法
遗传退火算法[16-18]的基本思路是在模拟退火的总框架中,把随机扰动产生新目标函数的模块改为遗传算法的相关模块(选择、交叉、变异)。这样程序的大循环是模拟退火算法的流程,而同一个退火温度中的内循环又是遗传算法的流程,其流程图如图3所示。这样既能克服模拟退火算法的缺点:扰动产生新解收敛时间比较长,又能克服遗传算法得到局部最优解(早熟)的缺点。
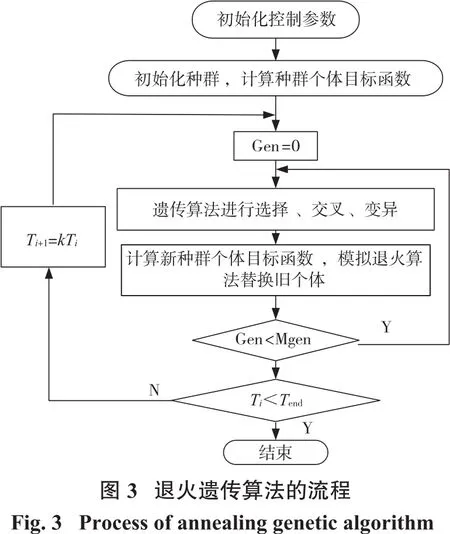
2.2 抛物线过渡理论
一次函数是最简单的转臂关节运动规划,但是此方法在启动与停止时候会出现大的角加速度,从而出现节臂的抖动,影响节臂的平稳性。为了避免这一情况,在启动与停止时使用抛物线过渡[15]如图4所示。
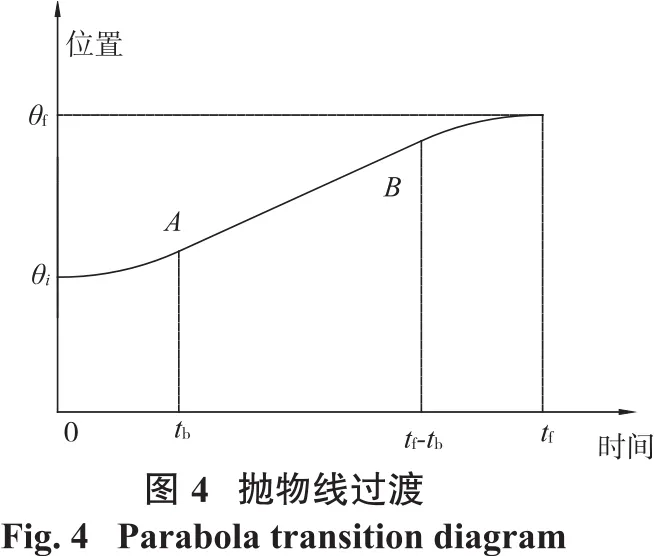
找到过渡时间的大小以及求出二次函数的常数项,整个关节运动轨迹就能求解。令起始时刻ti=0时关节的角度的位置为θi,得到ti-tb时抛物线方程为:
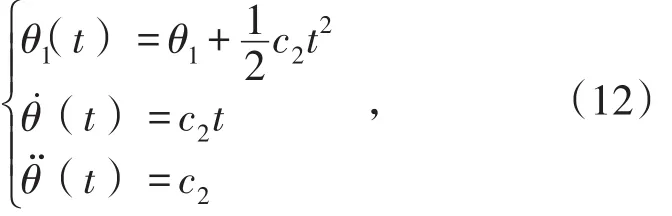
其中,t为关节运动时间;θ(t)为角位移函数;θ̇(t)为角速度函数;θ̈(t)为角加速度函数。
由文献[4]可得过渡时间tb与常数C2:
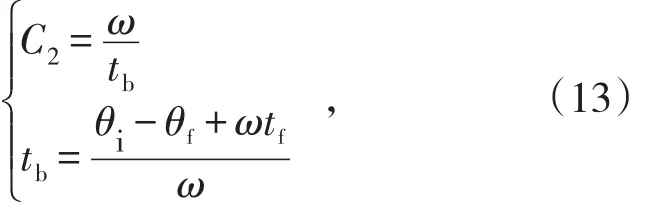
式中,ω为角加速度;θi为起始角位移;θf为终止是角位移;tf为运动总时间。
2.3 采矿转臂运动参数的优化
(1)设计变量。由过渡线理论[15]可知,其转臂的关节运动由初始角度、终止角度、匀速阶段角速度决定。而初始位置与终点位置是根据海底地形决定,其值可以由传感器测量。所以整个运动只需要确定匀速阶段的角速度,设计变量为3个关节匀速阶段的相对角速度:
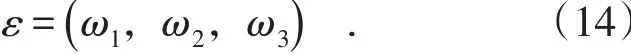
(2)目标函数。若驱动力矩变化小,则液压油压波动小,控制性能越好,所以以驱动力矩波动为目标。根据动力学模型可知,无论是水动力还是惯性力都与转臂间的角度、角速度、角加速度相关。而角度、角加速度又可以由其转臂关节实时角速度转换得到。根据抛物线过渡理论,匀速阶段的角速度决定了转臂的实时角速度。所以关节的驱动力矩可以由匀速阶段的角速度表示:
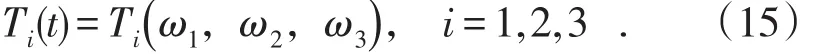
当驱动力矩小于其油缸的最大力矩时,节臂间的驱动力矩变化幅度最小,其油缸压力变化幅度也最小,从而运动平稳。所以以转臂在调整采矿姿态时驱动力矩变化幅度最小化为目标,则目标函数可以设置为:
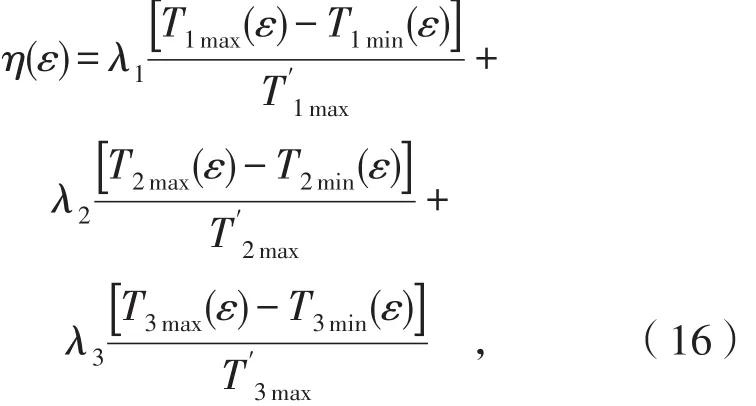
其中,T1ma(xε)、T2ma(xε)、T3ma(xε)分别为位置调整时关节1、2、3的驱动力矩最大值;T1mi(nε)、T2mi(nε)、T3mi(nε)分别为位置调整时关节1、2、3的驱动力矩最小值;T1
'max、分别为关节1、2、3的液压泵所能产生的最大力矩。考虑到关节1,2,3的驱动力矩是依次减少,所以加权系数可以设置为λ1=0.5,λ2=0.3,λ3=0.2。
(3)约束条件:由文献[19]可知,在转动角度、转动总时间不变的情况下,关节i匀速阶段角速度ωi由抛物线过渡时间tbi决定。根据抛物线过渡理论[15],tbi不能大于关节i调整总时间tfi的一半,则tbi其取值范围为(0,tfi/2)。根据tbi取值范围,根据文献[11]可以求解出关节i匀速阶段角速度ωi的范围;此外关节i驱动力矩不能大于其液压泵所能产生的最大力矩。所以其要满足的约束条件为:

式中,θii,θfi,tfi分别为关节i初始角度、终止角度及运动时间。
3 优化算例
若要使水平采矿姿态即θ1=θ2=θ3=0,转到姿态θf1=θf2=θf3=0.1,运动时间为tf1=tf2=tf3=2 s。液压泵能产生的最大驱动力矩分别为=1.0×10(5N·m)根据采矿转臂动力学系数如表1所示,采用遗传模拟退火算法优化节臂,其算法参数如表2所示,从图5所示的算法历程可以看出其收敛性良好。反应其驱动力矩波动大小的目标函数η(ε)=0.233,此时3个关节匀速阶段的角速度为ε(0.069 5,0.067 3,0.066 2)。根据过渡抛物线理论,代入设计变量,可以得到关节1、2、3的最优运动函数为分别为:
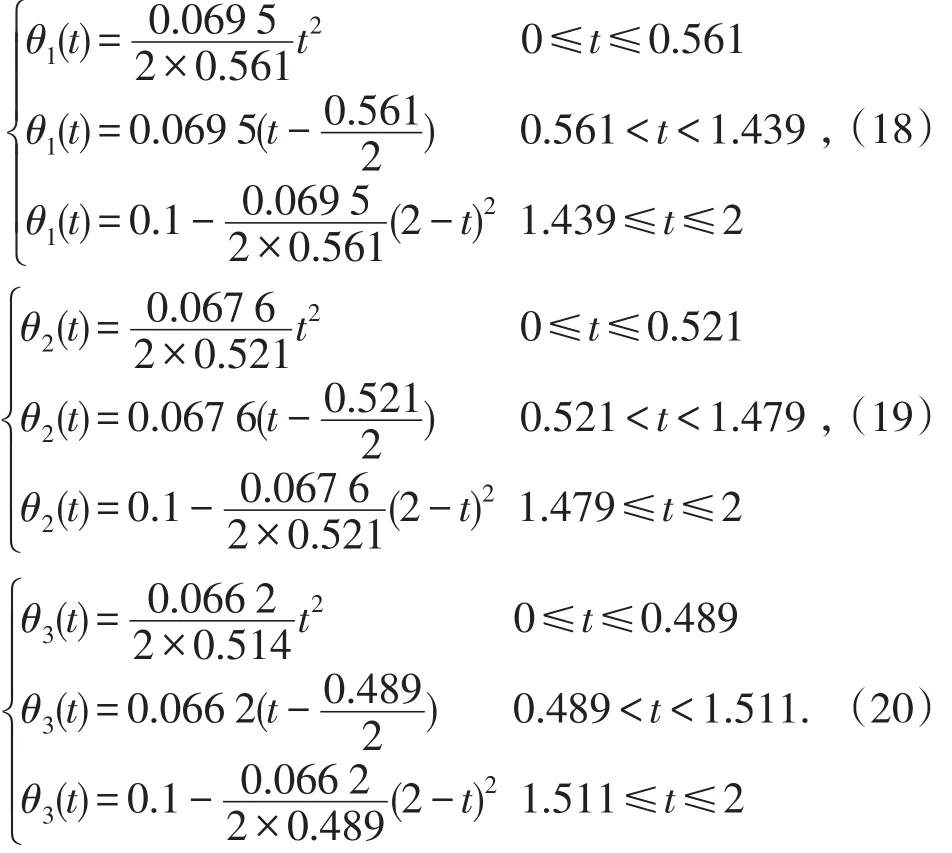
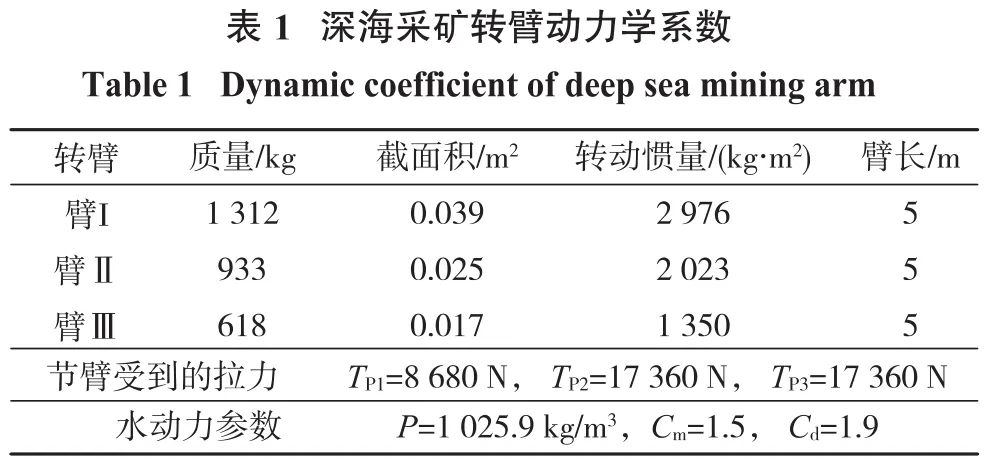
?
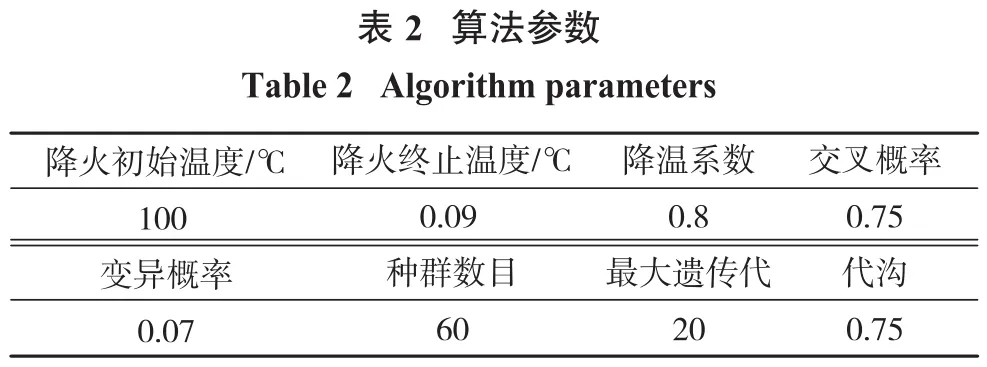
?

为了考察其优化后的结果,须与几种经典运动规划比较。运动规划Ⅰ为加减速时间与匀速运动时间相等,此时ε(0.066 7,0.066 7,0.066 7)。运动规划Ⅱ为匀速运动阶段时间为0,也就是先加速后减速,此时ε(0.095,0.095,0.095)。运动规划Ⅲ为加减速时间极短ε(0.055,0.055,0.055)。这3种运动规划矩波动是最小的。把几种规划的运动方程代入动力与遗传模拟退火算法所规划的对比如表3所示。由表3可知,经过遗传模拟退火算法所规划的关节运动学方程,可得其3个关节驱动力矩如图6所示,从图6可知关节1、关节2、关节3力矩是依次减少的,其采用优化算法后规划的力矩幅值最小,波动最小,运行最平稳。

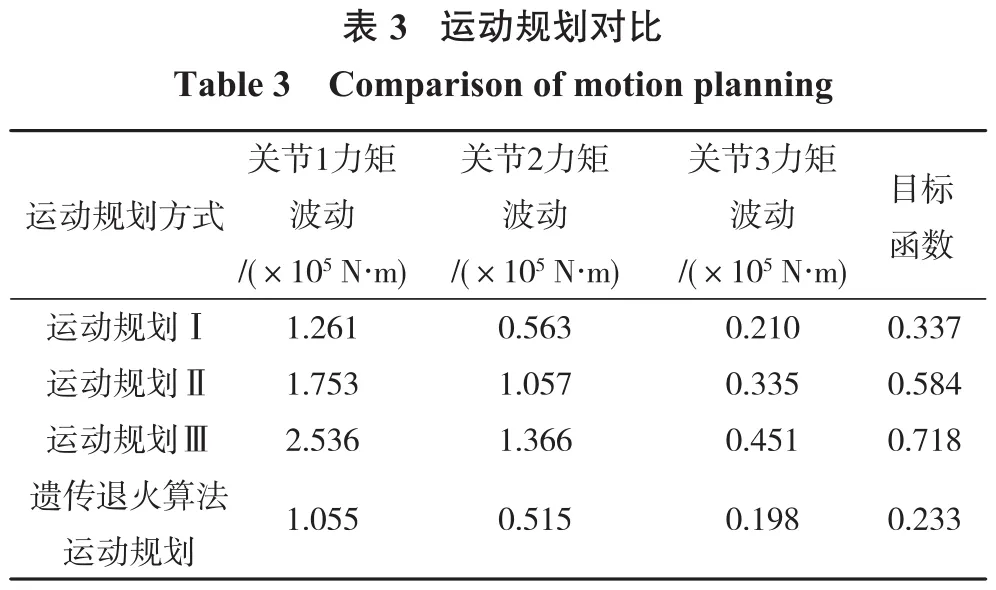
?
4 结论
本研究介绍了一种新型深海采矿方式——转臂支腿式采集方式,采用Kane法建立转臂深海姿态调整时的动力学模型,并在此基础上采用遗传退火算法对转臂运动进行规划,规划后其关节驱动力矩波动明显减少,从而整个系统的运动控制更加平稳。
