矿山短期生产计划优化的多目标遗传粒子群算法

2018-11-30叶海旺欧阳枧王李管王其洲

金属矿山 2018年11期

叶海旺欧阳枧李宁王李管雷涛王其洲

（1.武汉理工大学资源与环境工程学院，湖北武汉，430070；2.矿物资源加工与环境湖北省重点实验室，湖北武汉，430070；3.中南大学资源与安全工程学院，湖南长沙，410083）

矿山生产作业计划作为矿山组织生产的主要依据，关系到矿山能否高效合理地进行开采。而矿山的短期作业生产是整个矿山生产的基础，矿山的后期生产作业都是依托在短期作业计划之上，因此只有从源头控制成本、减少生产能力的浪费以及保证矿石质量、矿量的稳定，才能使矿床开采经济效益最大化［1-6］。

所谓露天矿采掘计划编制［7］就是确定一个能使矿山企业经济效益最大且在技术上可行的采剥顺序。从经济角度出发就是要使矿床开采过程中总净现值最大；从技术上可行就是在确保开采过程中总净现值最大外还要满足一系列技术上的约束，除了满足短期生产矿石量以及入选品位外，还需要满足每一个计划期内矿岩的开采量与选用的采剥设备的生产能力相匹配，另外各个台阶的开采还必须满足时空的发展关系。目前，国内编制露天矿短期生产计划主要还是依靠手工绘制方法［8］。此外，国内外也有很多专家学者借用优化法、模拟法实现编制矿山生产计划优化［9-14］。王李管等［15］借助于DIMINE矿业软件，根据矿山的原始地质资料建立了某矿的矿体、地表模型，结合该矿当前生产的实际数据，进行露天境界优化设计；胡乃联等［16］从露天矿采掘和运输成本的最小化角度出发，构建露天矿生产作业计划模型，并运用粒子群算法优化露天矿生产作业计划的编制，证明了运用智能算法实现优化露天矿生产作业的编制的可行性。

总体来看，目前对于露天矿山生产计划编制的研究主要是通过三维可视化软件，但使用三维可视化软件往往忽略每一计划期的矿岩开采量以及采剥设备的生产能力等约束；而部分运用数学规划方法建立露天矿山生产计划模型，再利用人工智能算法进行求解，大多在算法上进行创新，缺少在优化模型上的改进。本研究以某大型石灰石矿山为背景，从该矿山的品位及经济成本最小化的角度出发，以矿山某一生产期内月出矿品位、月出矿量和月生产利润为目标，采场的地质条件、采场的生产能力等为约束条件，建立该矿山短期生产计划模型，最后结合传统的粒子群算法与遗传算法对该模型进行求解，最终得到该矿山某月生产计划期内最佳的排产方案。

1 露天矿短期生产作业计划模型的构建

1.1 设计变量的选择

露天矿特别是大型石灰石露天矿在一个生产作业计划期内，由于开采矿石的分布（尤其是品位分布）不均，而选矿厂要求采出矿石品位与最佳入选品位不能出现较大浮动，同时还需要保证钙镁比（钙镁比是指矿石中CaO与MgO品位的比值）在一定的波动范围内。因此，会根据实际的生产情况多个不同品位矿点同时出矿，这就要求各个出矿点必须保证协调出矿。不妨以露天矿月生产计划期内各个出矿点日出矿量（t）为变量xij，其中i为不同出矿点的编号，i=1,2,3,…m；j为月生产计划期内的天数，j=1,2,3,…n，一般月生产计划为30 d。以xij为变量构建露天矿短期生产作业计划模型。

1.2 目标函数建立

在露天矿短期生产计划优化中，由于采取多个不同品位矿点出矿且选矿厂要求采出矿石品位与最佳入选品位不能出现较大浮动，因此要求矿山月生产计划期内出矿品位偏差最小目标；同时各出矿点需满足该月生产计划期内出矿总量，即要求与矿山预期出矿量偏差最小目标；每个矿点的出矿量及开采成本均不一样，所以不同矿点出矿会使得月生产计划利润产生很大的波动，月生产利润即为矿山开采产值与采矿成本之差，这就要求矿山在该生产计划期内生产利润偏差最小目标。其月出矿品位、月出矿量及月生产利润目标函数如数学表达式（1）～（3）所示。

（1）月出矿品位目标：

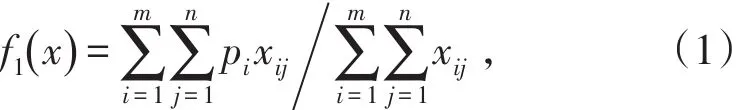
式中，pi为各个出矿点的矿石品位，%。

（2）月出矿总量目标：

（3）月生产利润目标：

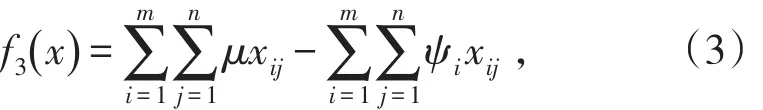
式中，μ为计划期内矿石的市场价格，元/t；ψi为第i个出矿点的吨矿成本，元/t。

一般而言对多目标函数求解还是比较困难的，因此不妨将多目标问题转化为单目标问题，而在众多转化方法中理想点法［17］适用性最强，其求解多目标规划问题时主要是各目标值尽可能逼近其理想（最优）值，通过比较与目标的接近程度选取最优解。其评价函数为：

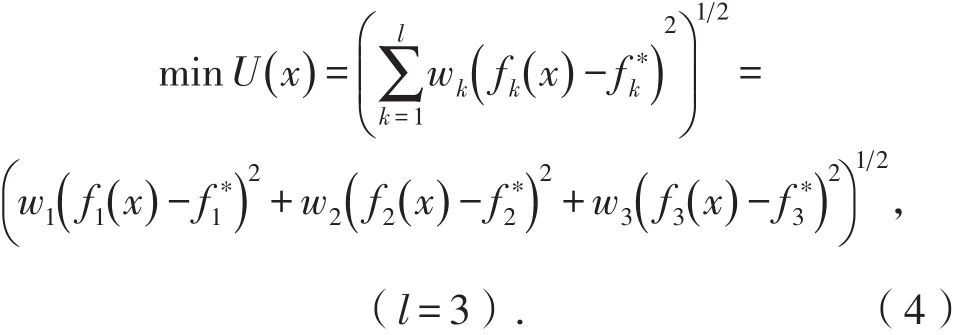
式中，fk(x)表示各分目标函数；为各分目标函数的理想值，其中为选厂要求的最佳品位，为月出最大矿量，为月生产利润期望最大值；权系数wi反映了在优化过程中对各分目标的侧重程度。

1.3 约束条件确定

露天矿山短期生产计划的编制受采场的地质条件、生产能力及生产原则等因素的影响。根据矿山的实际情况可列出如下约束条件。

（1）日采出矿量约束。考虑到露天矿超前采掘及采掘连续性的要求，各出矿点采掘量不能超过最大允许出矿量且不能低于最小允许出矿量。

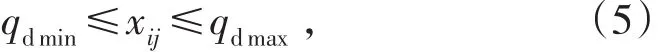
式中，qdmin为露天采场各出矿点日出矿最小量，t/d；qdmax为露天采场各出矿点日出矿最大量，t/d。

（2）日采出矿石品位指标约束。各出矿点为了满足选厂对于矿石入选品位的要求，日采出矿石平均品位允许在一个可接受的范围内，对应约束的数学表达为：式中，pi为各个出矿点CaO矿石品位，%；pmax为露天采场日出矿品位允许的最大值；pmin为露天采场日出矿品位允许的最小值，%。

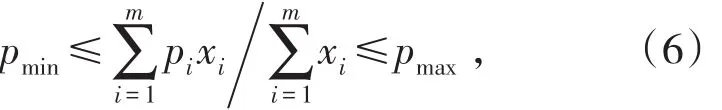
（3）日采出矿石钙镁比指标约束。各出矿点不仅要满足选厂对于矿石入选品位的要求，还需要合理搭配不同品位的矿石，保证最佳的钙镁比，对应约束的数学表达式为：

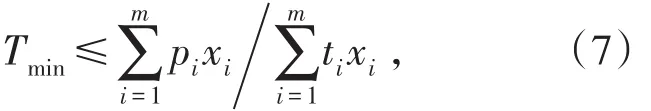
式中，ti为各个出矿点MgO品位，%；Tmin为露天采场月出矿钙镁比允许的最小值，%。

（4）设备能力约束。各出矿点出矿受到各个出矿点的采掘设备能力的约束，对应约束的数学表达为：

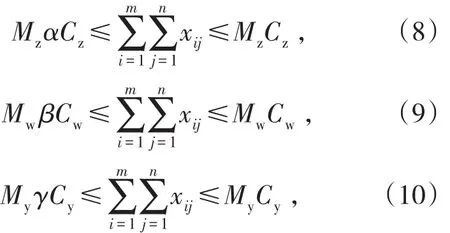
式中，Mz、Mw、My分别为凿岩、挖掘及运输设备在月生产计划期内的凿岩、挖掘及运输能力；α、β、γ为设备生产系数；Cz、Cw、Cy为凿岩、挖掘、运输设备数量。

（5）月计划期内出矿总量约束。月计划期内的矿石产量直接影响中长期计划制定是否合理，因此月计划期内出矿总量必须满足长期计划出矿总量的要求。

式中，Qmin为露天采场月计划期内最小出矿量，t。

（6）采场储量约束。在露天短期计划内，各出矿点出矿空间约束关系并不需要像长期计划考虑那么复杂，因此假设在当前条件下采场储量能满足该月计划期内的出矿总量。

式中，Q为露天采场月计划初的剩余可采矿量，t。

1.4 模型求解

本研究利用理想点法把复杂的多目标函数转化为单目标函数。为了在众多有效解中找出一个与各目标理想值都尽可能接近的解，本研究引用均差排序法确定权系数，首先在其可行域上极小化各分目标函数 fk(x)，得到极小点xk，得到：

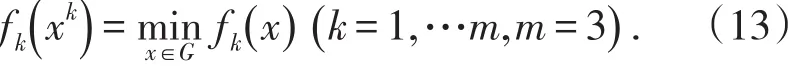
利用这k个极小点可以算出第k个目标函数关于各个极小点的相对离差。为了避免各目标函数值相差太大影响权系数的选取，对求取的相对离差作无量纲化处理。

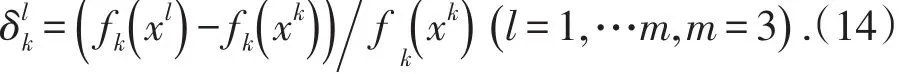
利用算数平均计算k个分目标函数关于各极小点的平均相对离差，于是得到：

由（16）式作为与各分目标函数对应的权系数。确定权系数后，将约束条件中的日采出矿石钙镁比指标约束及日采出矿量指标约束分别转化至月出矿品位及月采出矿量目标函数内，作为子目标函数，由于模型变量的增多，导致约束优化问题的搜索空间也急剧变换，这使得模型的求解变得异常困难，而粒子群算法是解决这类问题的最佳工具之一。粒子群算法不仅能用于求解离散空间组合问题，而且对于约束优化中的规划问题求解也非常有效。但是粒子群算法随着迭代次数的增加容易陷入局部最优解而无法跳出，因此本研究结合遗传粒子群算法对该多目标函数进行优化。对传统粒子群算法引入标准遗传算法中的交叉和变异操作：采用二进制单点交叉的策略将粒子处于的当前位置与在运动过程中产生的最佳位置作为父代进行交叉，对2个位置向量进行二进制编码并随机设定一个交叉点，在交叉点后的部分结构进行互换，形成粒子的子代；根据对群体中所有粒子设定的变异概率判断是否变异，对需要变异的粒子随机选择变异的位置进行变异，形成新的粒子子代。该方法改变粒子的前进方向，加快粒子搜索速度，既克服了传统粒子群算法易陷入局部最优的缺点，又加快了优化算法的收敛速度。

2 应用实例

2.1 矿山概况

某露天矿山属大型石灰石矿山，矿体沿东南走向，厚度达100 m，矿区由西南、东南2条上山公路到达矿区，矿山设计年产矿石量为1 446 324 t/a。为了达到年产矿石量，矿山采用分区开采，沿2条上山公路采用多个出矿点同时出矿，但由于作业地点分散、矿山设备多等显著特点，造成生产组织异常复杂，生产作业计划大多依靠人工经验，生产随意性强。针对这些情况，以该矿山2017年7月份已完成基建后4个出矿点同时出矿为研究对象，对该矿山7月生产作业计划进行优化。

2.2 短期生产计划编制数据

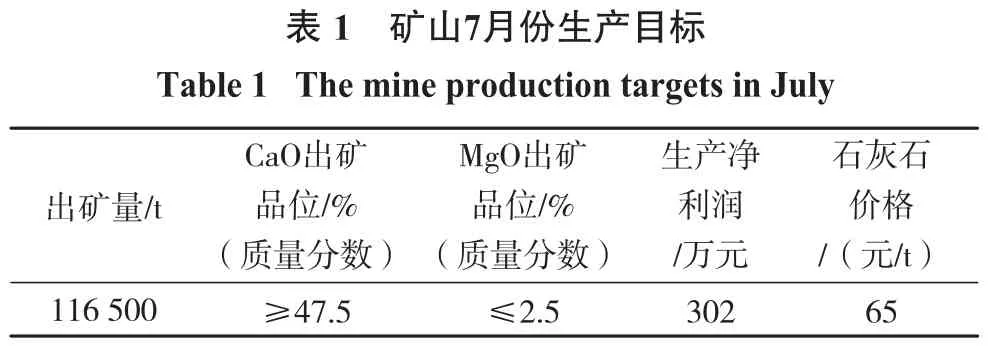
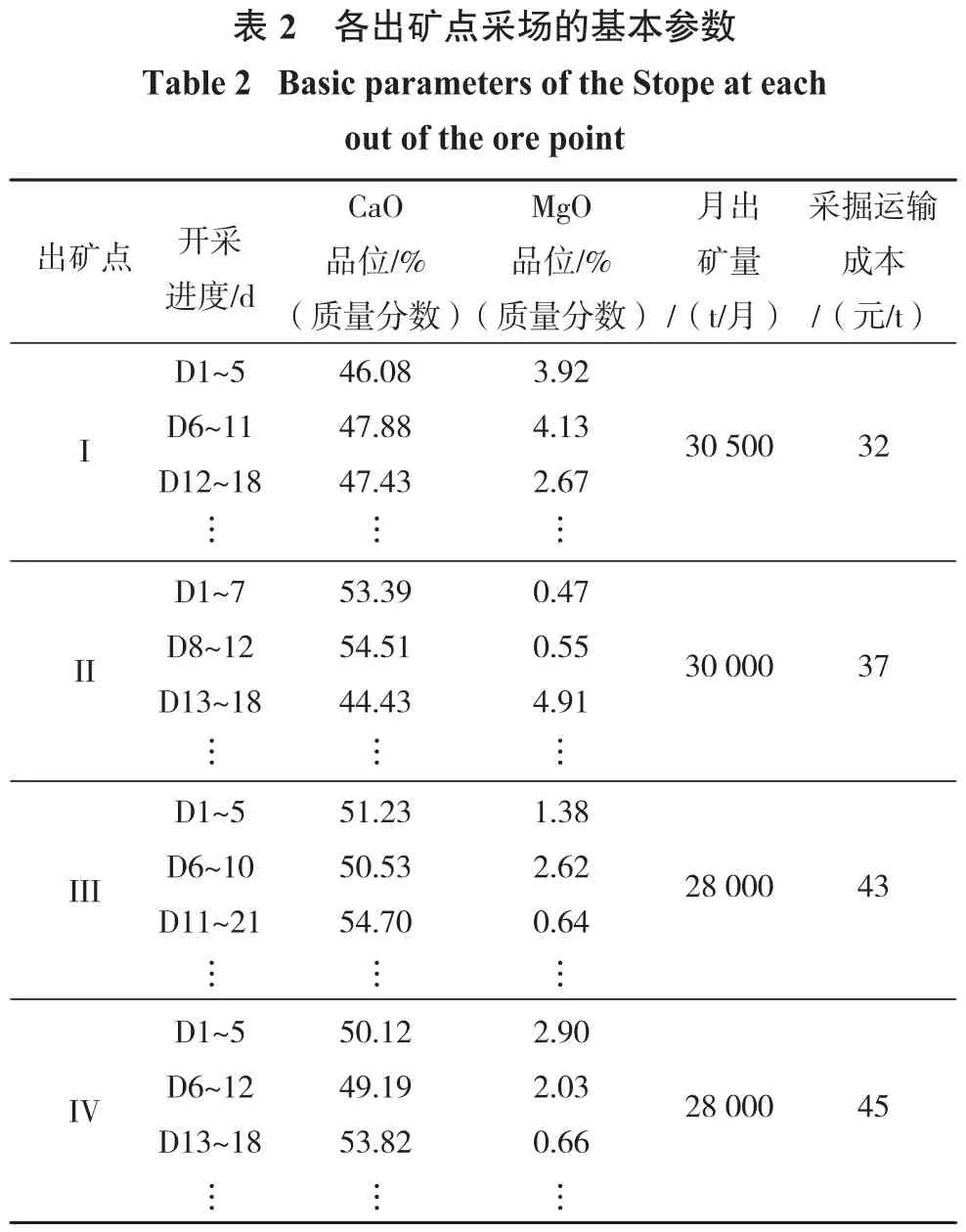
该露天矿山从每月的月初开始至该月份结束为1个生产月，根据矿山的年产计划要求，该月生产计划出矿量为116 500 t；日最大出矿量为4 821 t；日出矿最低品位为47.5%；最佳的钙镁比为大于19.0；月生产利润为302万元。矿区顶部由多个山头组成，最高标高496 m，当标高降至460 m水平时，将连成一片，形成较大的工作面。因此，根据矿山地形条件，已对部分475 m水平削顶，同时在矿区1#勘探线两侧进行460 m水平基建采准工作面，分别向东西两侧推进。矿山共4个矿层，沿走向推进；每个矿层根据采场的推移，矿石品位变化差异较大，可以保证各矿层多个出矿点开采的同时使得进厂的矿石可以进行充分混合，保证矿石品位长期稳定。矿山基建完成460 m水平东西2个工作面，即在该月份，矿山保有开拓矿量＞24个月，可采矿量＞12个月。表1为月生产目标，表2为各出矿点采场的基本参数。

2.3 模型求解

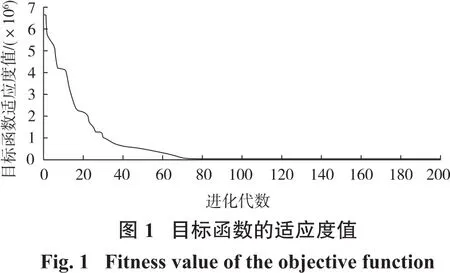
以矿山7月份为生产计划周期，综合考虑上述各相关约束，矿山月出矿量为116 500 t，日最大出矿量为4 821 t/d，月出矿品位约束指标上下限分别为41.35%、55.87%，将该月生产各分目标的理想值作为理想点，根据均差排序法计算各分目标的权系数为（0.45，0.32，0.23），该模型经遗传粒子群算法200步的迭代求解，得到如图1所示，目标函数最终适应度值趋近于0。

2.4 结果分析

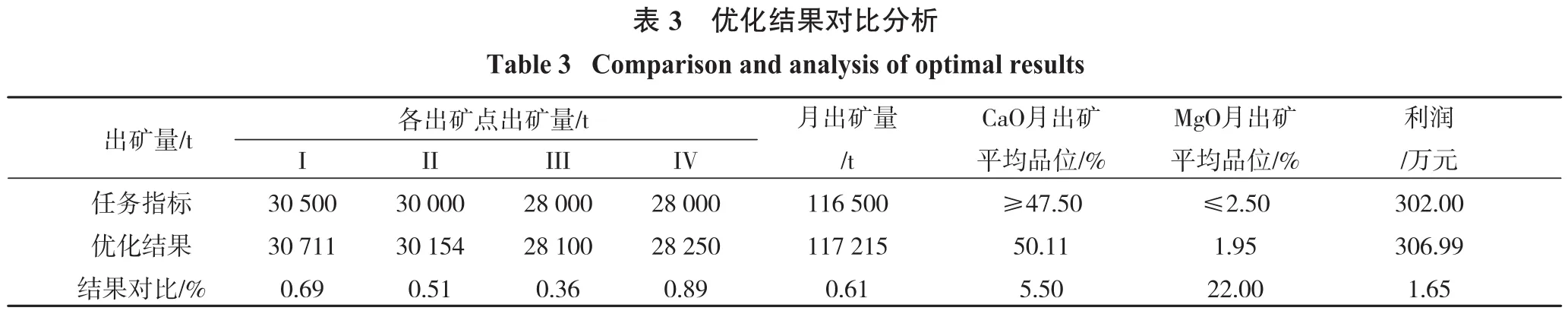
以该矿山7月份生产数据为例，优化结果如表3所示。

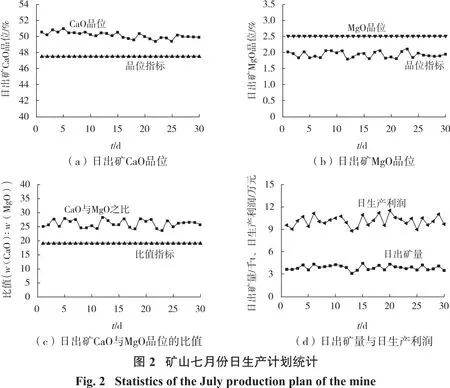
由表3可以看出该优化结果达到了该矿山月出矿量、出矿品位及月生产利润要求，其中各出矿点出矿量也与任务指标基本一致。根据优化结果统计矿山该月份日生产计划，如图2所示。

从图2矿山7月份日生产计划优化结果来看，在该生产计划期内矿山CaO日出矿品位最大值为50.93%，最小值为49.34%，计划月出矿品位为50.11%。偏差分别为+1.64%和-1.54%，经过优化后的日出矿石品位波动范围较小，同时满足选矿车间入选品位要求；月计划出矿MgO的平均品位为1.93%，达到入选品位要求；计划月出矿平均钙镁比最小值为23.7，满足高于19.0的生产要求；矿山日出矿量稳定在4 000 t左右，各出矿点及矿山月生产矿量均达到了矿山出矿要求；矿山日生产利润保持在10万元上下，日生产利润波动不大。该优化模型在误差允许范围内保证了矿山生产作业平衡。