逐级堆排尾矿泥浆排水固结规律试验

欧孝夺 苏 建 钟一和 吴光航 江 杰

（1.广西大学土木建筑工程学院，广西南宁530004；2.工程防灾与结构安全重点实验室，广西南宁530004；3.广西金属尾矿安全防控工程技术研究中心，广西南宁530004）

矿石选洗所剩尾矿泥浆经泵送排入尾矿库中堆储，具有含水率高、细粒含量多等特点［1］。由于缺乏有效的排水通道，尾矿浆经十几年时间仍未能完全固结，尾矿库内积水严重，极易引发漫顶、溃坝及库底泥浆泄漏等事故。通过增设“逐级湿堆尾矿排水装置”［2］为排水体，可有效加快尾矿泥浆横纵向排水固结。该排水装置以排水性能良好且能有效过滤细颗粒尾矿的土工排水材料作为竖向排水通道。排水材料下部固定连接至库底排水管，上部蜷曲于可随尾矿堆排同步升高的浮体中。随着尾矿泥浆的逐级堆排，排水材料自浮体中随之拉伸，过湿性尾矿上部积水及孔隙水随着这一排水通道持续性向下排水，最终从库底排水管集中排出。

尾矿的排水固结与尾矿类型、颗粒粒径、沉积时间、预压力施加时间等因素密切相关［3-5］，沉降量与沉降时间基本呈线性正相关关系，且浓度越高，相关系数越小［6］。尾矿泥浆的逐级排放工艺使尾矿土在饱和—非饱和状态中循环［7］，并在沉积层中形成交错层理［8］。巫尚蔚［9］将尾矿的一维自重沉积过程分为沉降阶段和固结阶段。但在增设排水体后，尾矿排水固结过程及渗流计算模型更为复杂，既有研究难以有效描述其在逐级堆排条件下排水固结过程的特性变化规律。

通过等比例模型试验模拟逐级堆排沉积条件下尾矿泥浆的排水过程，对该条件下尾矿横纵向固结效果进行了分析，并将尾矿排水固结分为5个阶段；进一步建立尾矿理想孔隙渗流模型，计算得到排水体最大影响半径时序曲线，为排水体作用下逐级堆排尾矿的排水固结提供参考。

1 排水固结模型试验

1.1 尾矿排水固结物理模型

从单次堆排过程来看，尾矿泥浆通过泵送排放至尾矿库内，随后悬浮泥浆通过竖向排水体排出自由水及孔隙水，土颗粒在自重作用下逐步固结，最终转变为具备结构强度的沉积土。而由于尾矿库采用间隔式的逐级堆排，故单次泥浆排水固结至一定程度后，下一次泥浆又会重新补充水分，使其固结状态发生改变。根据逐尾矿逐级堆排特点，建立其排水固结物理模型如图1所示。（1）分级填入既定厚度尾矿泥浆，排水体持续作业；（2）泥浆仅在自重作用下完成排水固结，故排水口在排水体下方；

（3）表层蒸发面及下端重力排水口为排水面，圆柱其余面为不排水面。

1.2 模型试验设计

（1）模型设计。根据上述物理模型设计制作等比例试验装置（如图2所示）。试验箱为高1.8 m，直径2.0 m的不锈钢圆筒，底部中心设置砂滤层排水口。排水口连接土工复合排水材料为竖向排水体，排水材料由表面滤网及骨架芯材2部分组成，上端固定在安装支架中，使排水体保持竖直。

（2）尾矿泥浆制备及堆排。所选尾矿为黏粒含量较大的铝土尾矿，矿泥取自中国铝业广西分公司2#尾矿库，经室内试验测试其基本性质如表1所示。

?

尾矿土样经过“晒干—初步粉碎—充分浸泡—搅拌”过程后制成20%浓度分散均匀的泥浆。堆排速率和每级堆排高度根据近2 a中国铝业广西分公司2#尾矿库实际情况，日排泥高度为0.07 m/d，堆排21 d后试验箱达到饱和。最终泥面高度达到1.475 m，水面高度达到1.747 m（如图3所示）。试验共持续125 d，其中前期堆排21 d，停排后继续测试104 d。

2 双向排水固结分析

2.1 孔隙水压力变化分析

试验布设9个孔隙水压力计（1#～9#），各位置孔隙水压力变化时程曲线如图3所示。孔隙水压力曲线存在一定波动，但总体上呈现明显阶段性。

（1）尾矿堆积高度每增加0.5 m，孔隙水压力平均减小约5 kPa；同一高度的各位置孔隙水压力随着与排水通道的距离的减小而减小，但减幅逐渐增大。

（2）堆排期孔隙水压力呈波浪式逐级递增，停排期孔隙水压力呈两段式逐渐减小，在约第35 d后下降速度明显放缓。孔隙水压力变化时间拐点与上层覆水排干时间吻合，故认为停排前期（第21～35 d）尾矿主要是在外加水头下产生渗流排出自由水，而停排后期（第35 d后）尾矿主要为固结过程中产生的渗流，尾矿压缩后所含的孔隙水被排出，渗透性降低，孔隙水压力值减幅变小。

2.2 沉降变化分析

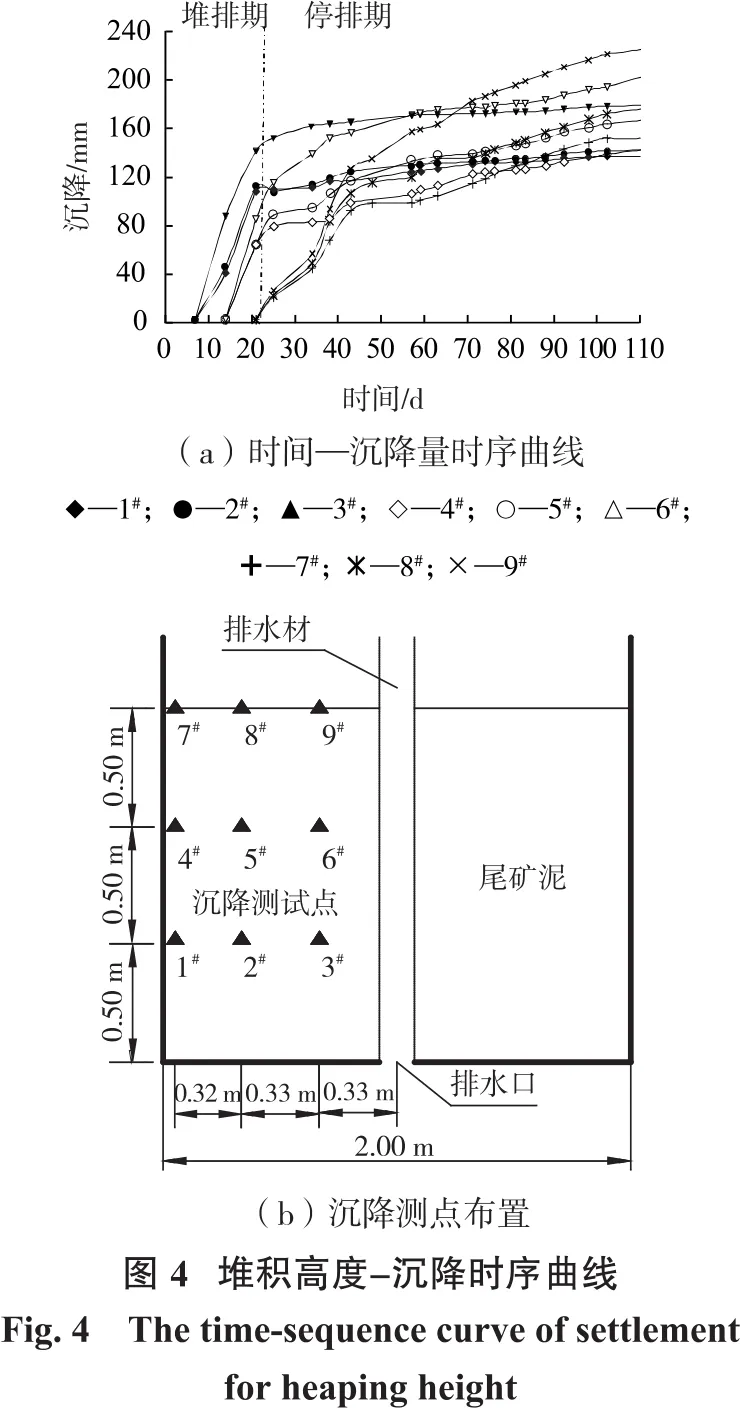
试验共布设沉降标9个（1#～9#），从堆排8 d后（堆填高度0.5 m布设第一层）开始测量，各位置沉降时程变化曲线如图4所示。

从图4来看，双向沉降变化与孔隙水压力变化并不同步，土体应力变化滞后于应变变化。

（1）对于不同高度的沉降测试点，下层土的沉降很快达到稳定，且单层变形量更大。最终底层（1#～3#）平均单层沉降变形152.6 mm，远大于上层（7#～9#）的平均单层沉降变形22.7 mm；对同一高度的各沉降值点，随着渗流路径增加沉降量越来越接近，且该规律随深度增加越发明显，底层距离排水材料0.66 m与0.98 m位置沉降量几乎相等。

（2）底层及中间层沉降测试点（1#～6#）的沉降曲线可分为2个阶段：堆排期（21 d前）逐级堆载与排水同时进行，沉降降幅较大；停排期（21 d后）仅通过排水固结压缩尾矿体，沉降明显放缓；尾矿表层沉降测试点（7#～9#）自停排后开始安装，沉降拐点与底层及中间层不同步，除向下排水外其表面还受到蒸发作用长期影响，试验后期沉降增幅明显高于底层及中层。

2.3 逐级堆排尾矿排水过程分析

尾矿在竖向排水体作用下，由完全扰动的水土混合悬浮泥浆转化为土水分离的结构性沉积土，该沉降及自重固结过程亦是泥土系统（悬浮态泥和沉积态土共存的系统）内颗粒间从无接触应力到产生有效应力的过程。Imai［10-11］认为固结过程主要存在3个阶段：絮凝阶段、沉降阶段及固结阶段，张楠［12］在Imai研究基础上进一步提出对于“泥—土系统”最终形成沉积土的演化过程。

通过模型试验模拟分级堆排的简化过程，基于上述对不同位置孔隙水压力、沉降时序变化分析，可将尾矿的沉积固结过程划分为5个阶段。

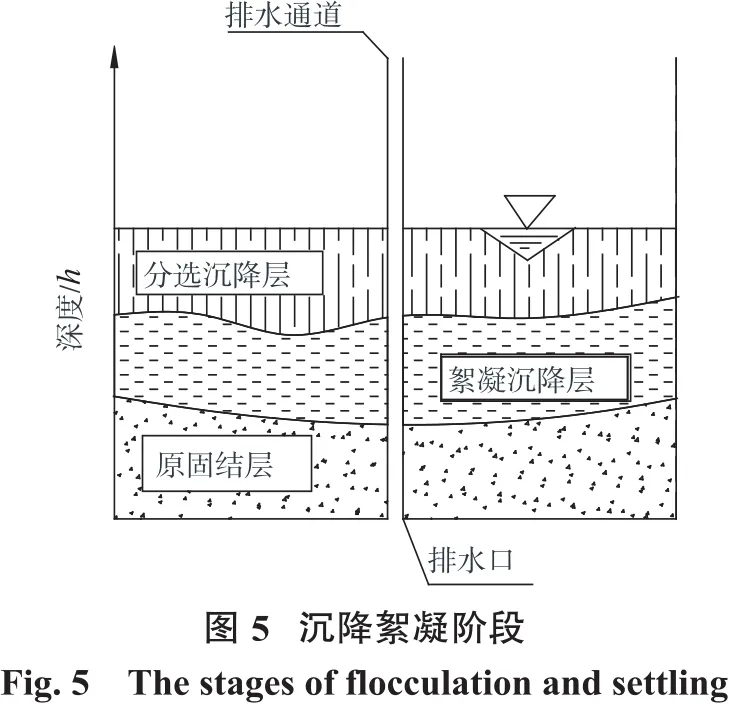
（1）沉降絮凝阶段。尾矿浆排放初期，由于水力冲击、搅动及重力作用，尾矿颗粒产生剧烈运动，此时液面浑浊。但由于土颗粒密度大于水的密度，呈现下沉运动并表现出集合沉降的倾向。当土颗粒间电解质浓度达到临界絮凝浓度时，土颗粒在布朗运动、不等速沉降、以及水流紊动引起的碰撞作用下会迅速产生絮凝［13］。尾矿浆上下呈现分选沉降层和絮凝沉降层（如图5所示）。

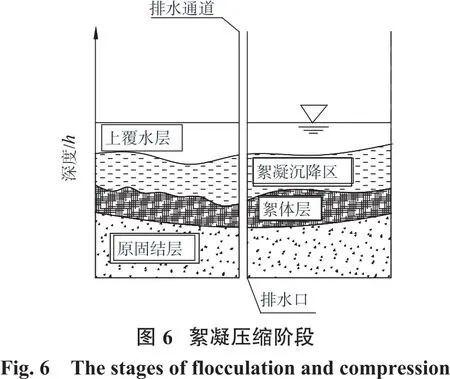
（2）絮凝压缩阶段。沉降絮凝阶段后，絮凝沉降层的尾矿颗粒大多结成絮团并沉底（如图6所示）。随着排水的进行，絮团在底部受重力和布朗运动的双重作用，开始相互紧密接触，絮团间的毛细水被挤出，胶体颗粒间的电磁力不断增加，同时也伴随着孔隙的形成［14］。最终，絮团全部转换为絮体，沉降区消失。

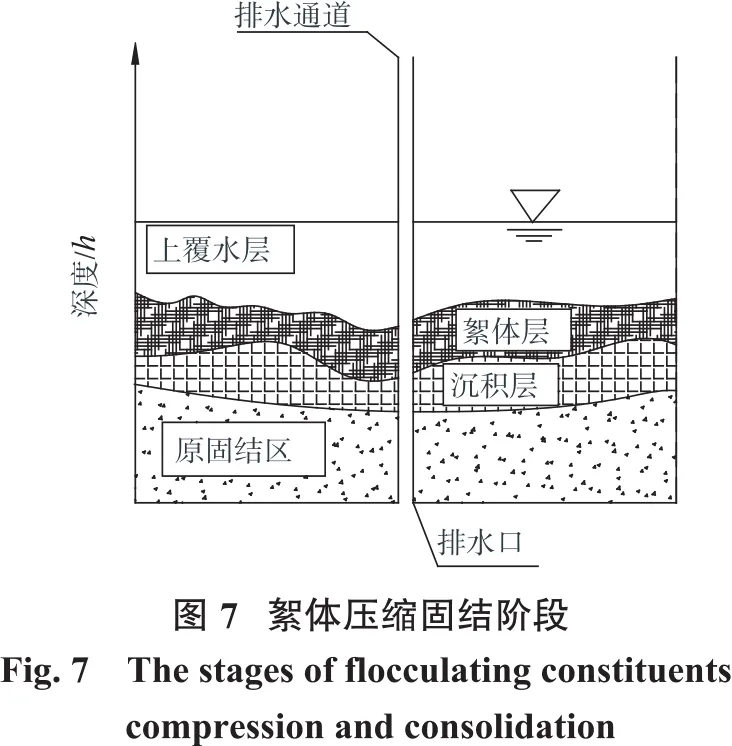
（3）絮体压缩固结阶段。随着絮凝压缩的进行，上部压力使得絮体距离逐渐减小，絮体区的下部开始固结形成结构性沉积土（如图7所示），絮体间的电磁力连接开始转变为土颗粒间有效应力［15-16］。排水通道附近的沉积土在水头差的作用下开始通过排水体滤膜排水。随着渗流的进行，尾矿土的孔隙不断减小，固结程度逐渐提高。

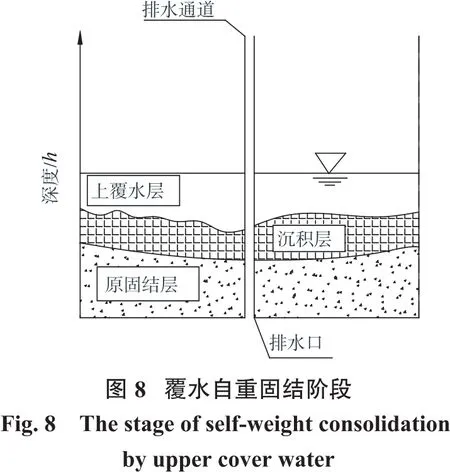
（4）覆水自重固结阶段。絮体在上覆压力及自重作用下全部压缩并转化为结构性沉积土（如图8所示）。尾矿泥浆完成水土分离，上层覆水通过竖向排水体快速排出，超静孔隙水压力逐渐消散，尾矿体积不断压缩，土颗粒间有效应力逐渐增大。由于排水速率快，该阶段尾矿的固结速度最高。

（5）自重压缩固结阶段。上层覆水排干后（试验中为35 d后），尾矿进入自重压缩固结阶段。随着水位逐渐降低到尾矿泥表面以下位置，渗流场转变为以土颗粒中孔隙水渗流为主要渗流形式，渗流速率及土体压缩速率减缓。随着排水过程的持续，尾矿上部呈现非饱和土区并逐渐向下加深。最后在自重作用下土体压缩至稳定，孔隙水压力及沉降几乎不变化，自重固结完成（如图9所示）。

3 渗流模型及最大影响半径

3.1 尾矿理想孔隙渗流模型建立

水头差使饱和尾矿泥内水体在尾矿孔隙内流动，水体所受土颗粒浮力的反力与水渗流所受阻力互为作用力与反作用力。沿渗流流线方向取一微分单元体，建立理想孔隙渗流模型（如图10所示）。

从图10模型中取独立圆柱形微分体（下称微分体）进行受力分析，设渗流起始端a处水头为h1、面积为A1；渗流终端b处水头为h2、面积为A2；孔隙流体长度为L。作用在微分体的截面a、b处的边界压力（孔隙水压力）分别为：

式中，γw为水容重；其中PWa方向与渗流同向，PWb方向与渗流反向。

水体自身重力沿ab方向的分力为：

式中，γw为水容重；n为土的孔隙率；l为微分体长度；A为微分体截面积；α为渗流方向与竖直面夹角。

水体所受土颗粒浮力的反力等于与土颗粒同体积水重，其在ab向上的分力为：

水渗流时微分体土颗粒对其施加总阻力为：

式中，T为单位水渗流受到的阻力，其方向与渗流反向。

微分体受力如图11所示，建立其平衡方程：

引入单位尾矿上的渗透力Gcr，其与阻力T互为作用力与反作用力。同时，将孔隙水压力u1引入平衡方程式（6），得：

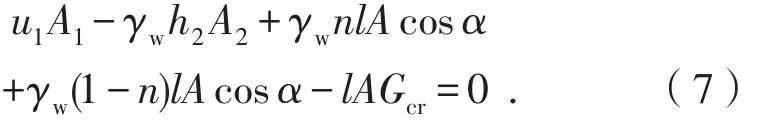
移项整理后，可得孔隙水压力u1为：

由式（8）可知，渗流起始位置的孔隙水压力值u1与水位h2、孔隙渗流面积A1及A2、孔隙率n及单位尾矿上的渗透力Gcr各变量呈非线性关系，随各变量离散性变化而不断改变。

3.2 孔隙水压力变化机制分析

尾矿泥浆沉降絮凝初期，悬浮状颗粒间不产生接触应力，仅受自身重力及水浮托力γwVS作用并缓慢下沉。沉降过程中，颗粒间由悬浮状态或边—边接触逐渐过渡为面—边、面—面形式接触，同时伴随着大孔隙和中等孔隙发育；随着排水固结的持续进行，土颗粒开始接触，有效应力不断增加，尾矿颗粒逐渐由蜂窝状结构向更为致密的絮凝状结构转化，土的骨架初步形成，骨架中孔隙构成稳定的渗流通道。

取排水过程的某一时段进行分析，假设该时段的初始孔隙水压力为u10，结束时的孔隙水压力为u11。根据式（8）可得孔隙水压力分别为：

式中符号与式（8）相同。

为方便讨论，现做出以下假设：

（1）渗流路径近似为水平向，即 cosα=0；

（2）所研究的渗流孔隙路径始于各孔隙水压力计，终于排水管壁，则式（9）、（10）可简化为：

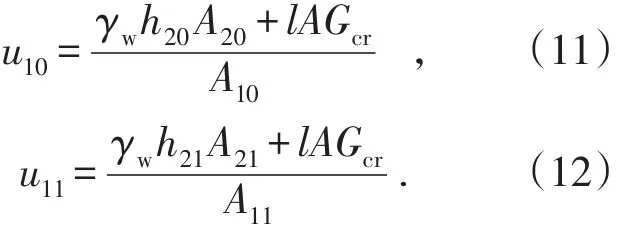
由于排水体处于整个尾矿泥中心且上下贯通，孔隙水渗流进入竖直排水体时将由水平运动变为垂向运动，故可用井损折减系数β替代试验中水流偏转产生的水头损失，则渗流末端的水头高度可表示为：

式中，hw为竖向排水体水位高程。可知，孔隙水压力变化值为：

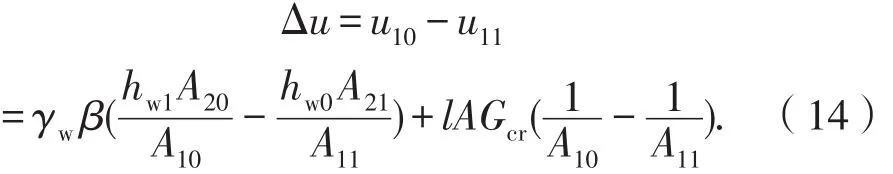
由式（14）可见，尾矿孔隙及水位差变化使得孔隙水压力逐渐消散。

尾矿泥浆堆排初期，竖向排水通道内水位较低，孔隙的两头形成水位差，从而使孔隙水沿着孔隙发生渗流。随着排水过程的进行以及上覆荷载的持续作用，孔隙不断被压缩，等效截面积A减小，加上孔隙间水头hw也同步减小，尾矿渗流越发困难，孔隙水压力逐渐趋于稳定。

3.3 最大影响半径确定

最大影响半径边界处不发生渗流，即孔隙水压力变化梯度为0，可表达为：

式中，Δu为孔隙水压力消散量；l为该位置与竖向排水通道的距离。

将式（14）Δu代入式（15）得：

由2.2节可知，式（16）中孔隙面积A及水位高度均会随固结过程而逐渐减小，所以最大影响半径亦是随时间而变化的函数。根据最大影响半径定义［17-18］，随着渗流长度的增加，尾矿孔隙水压力下降值逐渐变小。当孔隙水压力下降值不随距离变化时，该位置与排水体距离即为排水体最大影响半径。为了解尾矿固结过程中最大影响半径变化特征，以天为单位对尾矿各个位置孔隙水压力下降值进行统计分析。考虑到底部尾矿受不透水边界条件影响，渗流条件与上部不一致，故只对0.5 m及1.0 m堆积高度的4#～9#孔隙水压力计进行分析。根据之前测试数据，自第35 d后各层孔隙水压力变化变缓，即影响半径变化趋于稳定，故仅对堆排期第11～21 d及停排期的第22～35 d进行统计。

通过对试验箱半径内的不同位置孔隙水压力下降值统计分析，将各断面孔隙水压力下降值曲线进行拟合预测以确定其最大影响半径值。选用不同函数拟合后发现，当选用指数函数（y=ae-ex）拟合时R2值最高，各拟合曲线的R2在0.841 8～0.995之间，曲线的拟合值与实际值相关性较好。故选用指数函数拟合每天0.5 m及1.0 m堆积高度断面孔隙水压力下降值曲线，得到最大影响半径，统计后绘于图12。

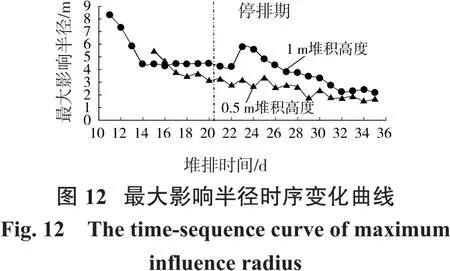
由图12可见，最大影响半径随着堆排时间增加，总体上呈逐渐减小趋势。但由于孔隙水压力受温度、大气压等因素影响，加上各曲线拟合R2值不一所形成的可靠性差异，最大影响半径时序变化曲线存在一定波动性。堆排第1 d 0.5 m及1.0 m堆积高度排水体影响半径分别达到8.34 m及5.46 m，下部最大影响半径明显大于上部；之后最大影响半径迅速衰减，并在第4 d出现明显拐点，减小速率变缓；堆排完成15 d后，0.5 m及1.0 m堆积高度排水体影响半径分别稳定在约2.2 m及1.7 m。这印证了排水体最大影响半径变化主要是受尾矿固结程度的影响。固结前期尾矿孔隙较大，排水体可以通过较长的渗流通道作用；而随着上覆荷载的增加，尾矿的固结程度不断提高，骨架被逐渐压缩，渗流孔隙通道变得狭窄或是被渗流过程土颗粒阻断，渗流难度增加，渗流场范围逐渐减小。

4 结论

（1）从纵向上看，孔隙水压力值、沉降变化与堆积深度成正比，但二者增幅并不相同；从径向上看，同一高度的孔隙水压力与沉降值随渗流路径增加降幅均逐渐减小，且随深度增加该规律越发显著。

（2）停排后（第21 d后）上覆荷载逐渐减小，使下层沉降增幅明显减小；而孔隙水压力则是在停排后呈两段式减小，在上层自由水排干后（第35 d），孔隙水压力降幅明显减小。说明孔隙水压力与沉降在土体排水固结过程中变化并不完全同步，应力变化滞后于应变变化。

（3）根据沉降及孔隙水压力变化曲线可进一步将逐级堆排尾矿排水过程分为沉降絮凝阶段、絮凝压缩阶段、絮体压缩固结阶段、覆水自重固结阶段及自重压缩固结阶段5个阶段。

（4）建立了尾矿理想孔隙渗流模型，孔隙水压力与水位、孔隙渗流面积、孔隙率及单位尾矿上的渗透力呈非线性相关，并基于孔隙水压力数据拟合测算各时期不同高度排水体最大影响半径。随着尾矿的固结程度不断提高，渗流场范围逐渐减小，影响半径在约4 d内迅速衰减，第35 d后0.5 m及1.0 m堆积高度影响半径分别降低至约1.7 m及2.2 m。