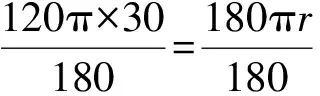弯弓射箭 考出素养*
——2018年浙江省金华市数学中考第16题PISA类试题的设计
2018-11-30
●
(金华市教育局教研室,浙江 金华 321017)
PISA数学素养是PISA评估的3个主要内容之一,强调在真实问题情境下数学化过程中的数学参与、数学运用及其应当具有的数学意识和问题解决中“表述”“运用”“阐释”的数学能力,其考查过程很好地描述和评价了学生的数学素养.
因此,试题的设计应着眼于对数学“核心素养”的考查,需要问题情景、思考过程和反思应用来体现数学思想.在问题情景中,发现数学问题,联系所学知识,尝试探究解决,来实现对学生建模能力、探究能力、实践能力和创新能力等核心素养的考查[1].现以2018年浙江省金华市数学中考试题填空题第16题的命制过程为例,来探讨PISA理念下的试题编制.
1 设想计划
根据试卷双向细目表,填空题的最后一题设计为几何建模问题,其情境与生活实际相联系,选择学生熟悉的背景,抽象出几何图形,借助学生平时数学活动经验的积累,把观察、探究、计算融合在一起,蕴含方程函数、数形结合以及转化的数学思想方法,来体现PISA理念[2].
2 灵感追溯
近日,笔者在清华大学艺术博物馆欣赏了法国雕塑家布德尔“拉弓的赫拉克勒斯”铜像,赫拉克勒斯是希腊神话中的英雄,在两块巨石上,赫拉克勒斯叉开双脚顶在上面,脚趾因为用力而弯曲,全身肌肉隆起.他颧骨突兀,眼睛圆睁,神情严肃而威严.他一手握弓一手拉弦,整个身体向后用力坐,弓被拉得弯曲,形成一道优美的弧线,仿佛在向世人展示他无与伦比的力量,巨大的弯弓和舒展的四肢,形成激烈的动感和独特的构图.
在欣赏、感叹布德尔的作品时,仿佛看到赫拉克勒斯弯弓射箭的整个过程,思考为什么会产生如此动感中的平衡,体现这位英雄的力量之美.当把虚无的弓弦补上的时候,发现箭就在弓弦的中垂线上.为此,能否以此素材为情景,在拉弯弓射箭的过程中,假设弓都保持圆弧,用数学的眼光、数学的思维来欣赏作品、研究作品,达到对这一主题思考的深度呢?
3 改编历程
方案1如图1是小明制作的一副弓箭,点A,D分别是弓臂BAC与弓弦BC的中点,假设弓臂BAC是圆弧形.测得AD=10 cm,BC=60 cm,求弓臂BAC所在圆的半径.
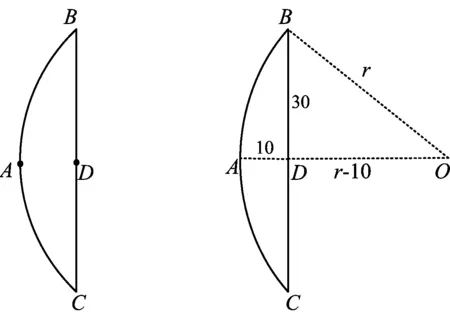
图1 图2
如图2,作出该圆的圆心O后,在Rt△BDO中,BD2+OD2=OB2,即302+(r-10)2=r2,求得圆的半径r=50.
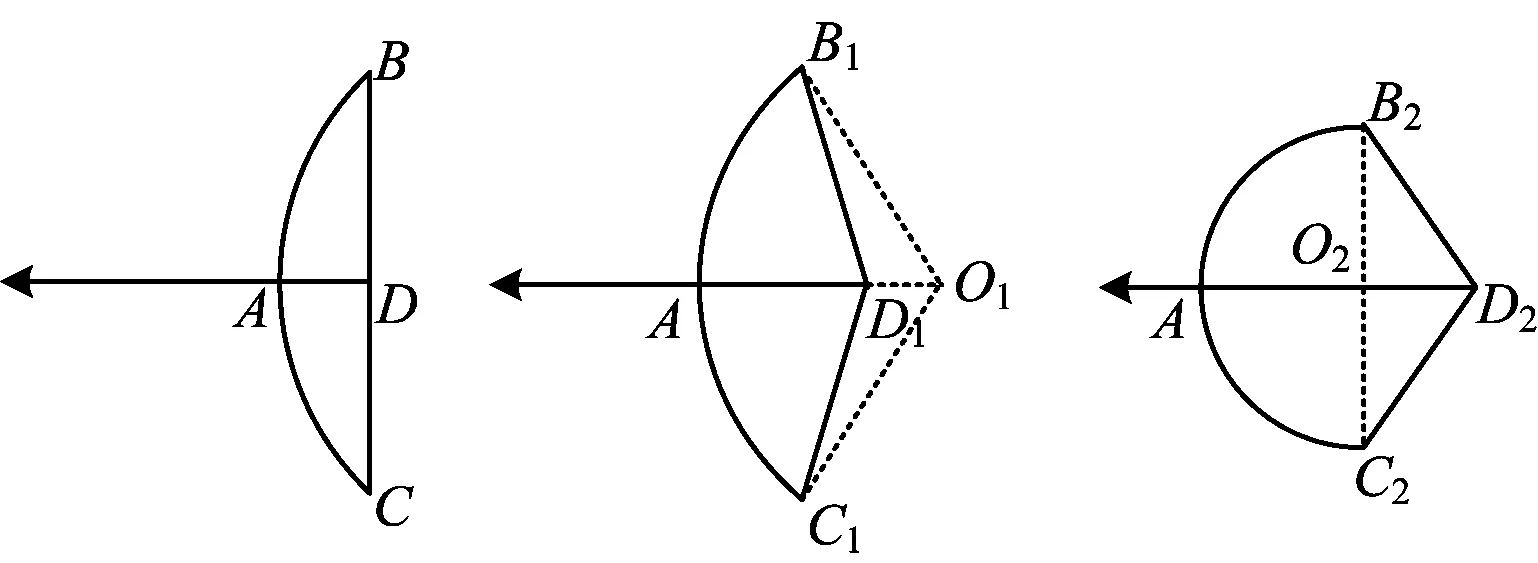
图3 图4 图5
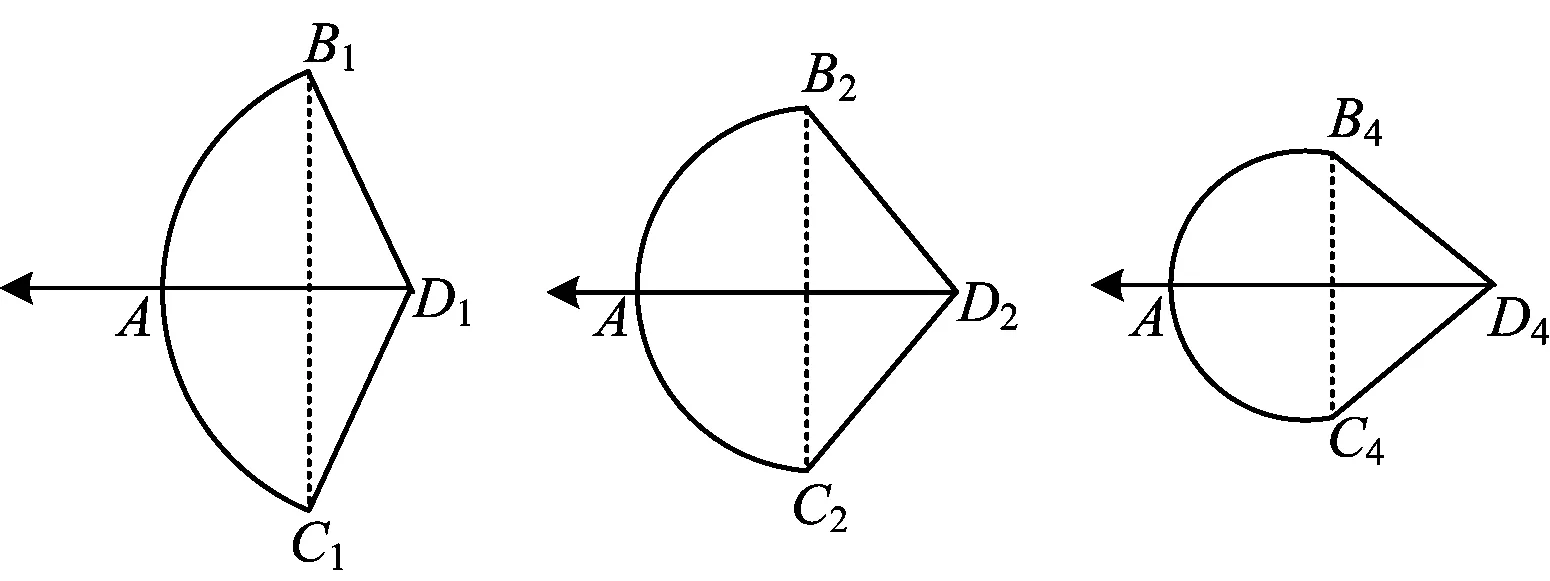
图6 图7 图8
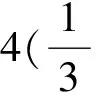
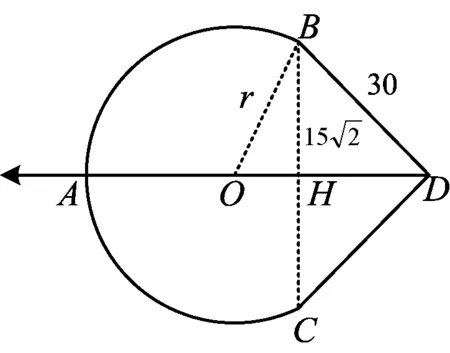
图9

弓臂BAC所在圆的圆心为O,在Rt△OBH中,
BH2+OH2=OB2,
即
求弓箭的弓臂长度,有一定的实际意义,将等腰三角形的轴对称、垂径定理、三角函数、勾股定理等有机整合一起,很好地考查了圆的相关知识,特别是垂径定理应用、Rt△OBH的构造,有一定的思维要求.但在拉弓射箭过程中,弓臂BAC的不变性没有很好的体现.因此,能否选择两种特殊的情况,适度整合,利用其中弓臂、弓弦长度的不变性,结合两种不同情况之间的联系来设计问题.利用图8,尝试联系圆的切线,形成方案3.
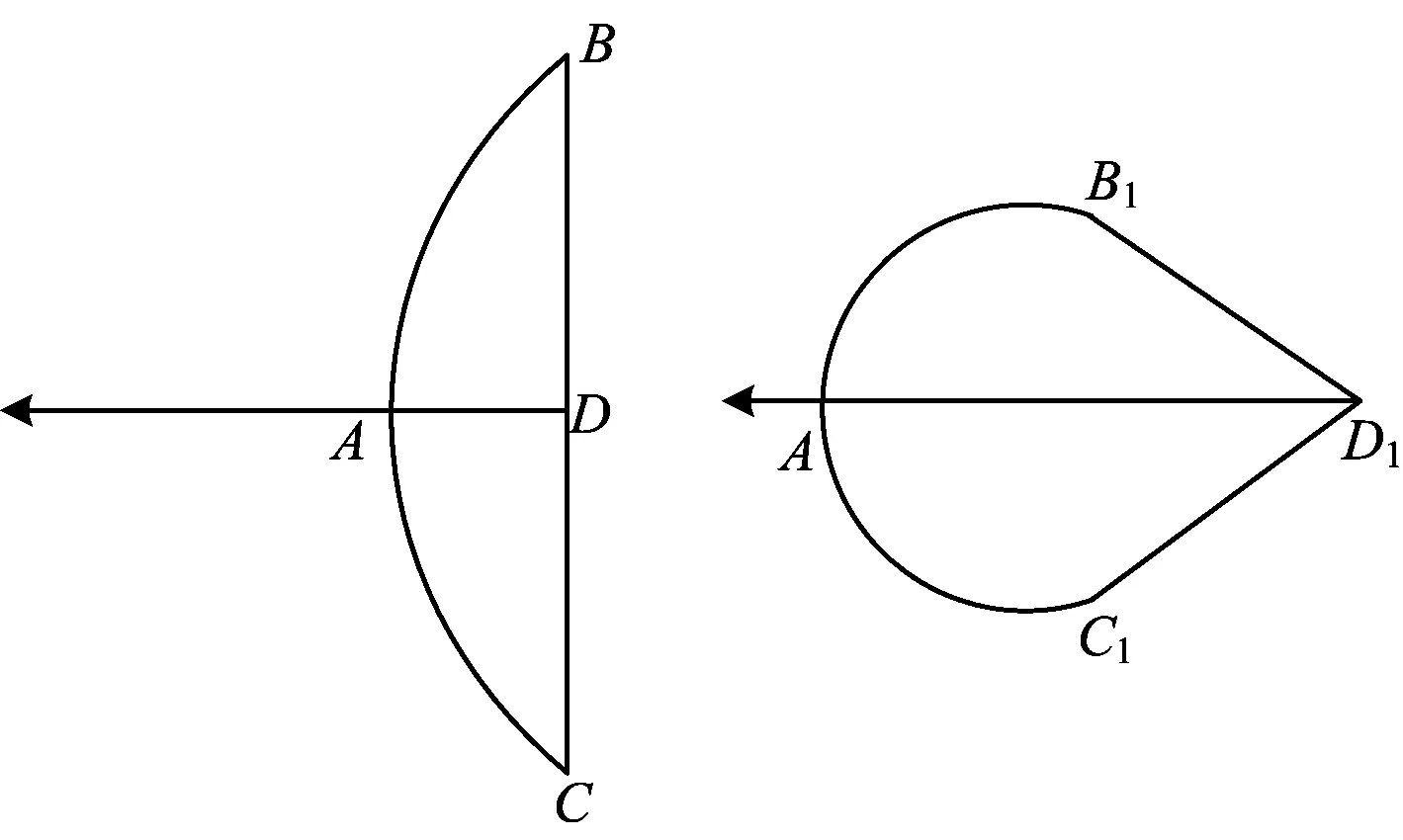
图10 图11
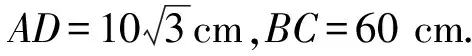
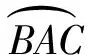

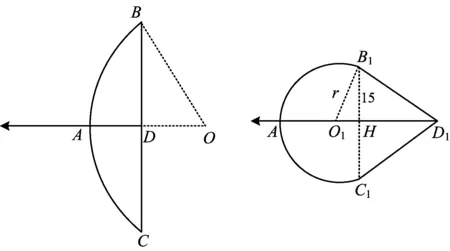
图12 图13

得出n=240°,这样就可以得出∠O1B1D1=90°,说明B1D1与弓臂B1AC1所在的圆相切.
本方案中,将有关圆这部分的核心内容,如垂径定理、切线的判定、弧长的计算等有机地融合在一起,达到了核心内容重点考察的目的.通过计算得出∠O1B1D1=90°来判定B1D1是圆的切线,改变证明切线的常用背景,即通过角的转化来证明直线与半径垂直,有一定的新意.联结B1C1后得出∠B1D1A=30°,学生很容易得出∠B1O1D1=60°,有很大的迷惑性,需要学生对图形有清晰的理解,能很好地甄别学生不同的思维水平.
但是,本题第1)和第2)小题都是有关垂径定理的应用,通过构造直角三角形、利用勾股定理转化为方程求解,得出的方程基本一致,考查雷同.另外,判断B1D1与弓臂B1AC1所在圆的位置关系,在拉弓射箭过程中,其现实意义不大.

方案4(定稿) 如图14是小明制作的一副弓箭,点A,D分别是弓臂BAC与弓弦BC的中点,弓弦BC=60 cm.沿AD方向拉动弓弦的过程中,假设弓臂BAC始终保持圆弧形,弓弦不伸长.如图15,当弓箭从自然状态的点D拉到点D1时,有AD1=30 cm,∠B1D1C1=120°.
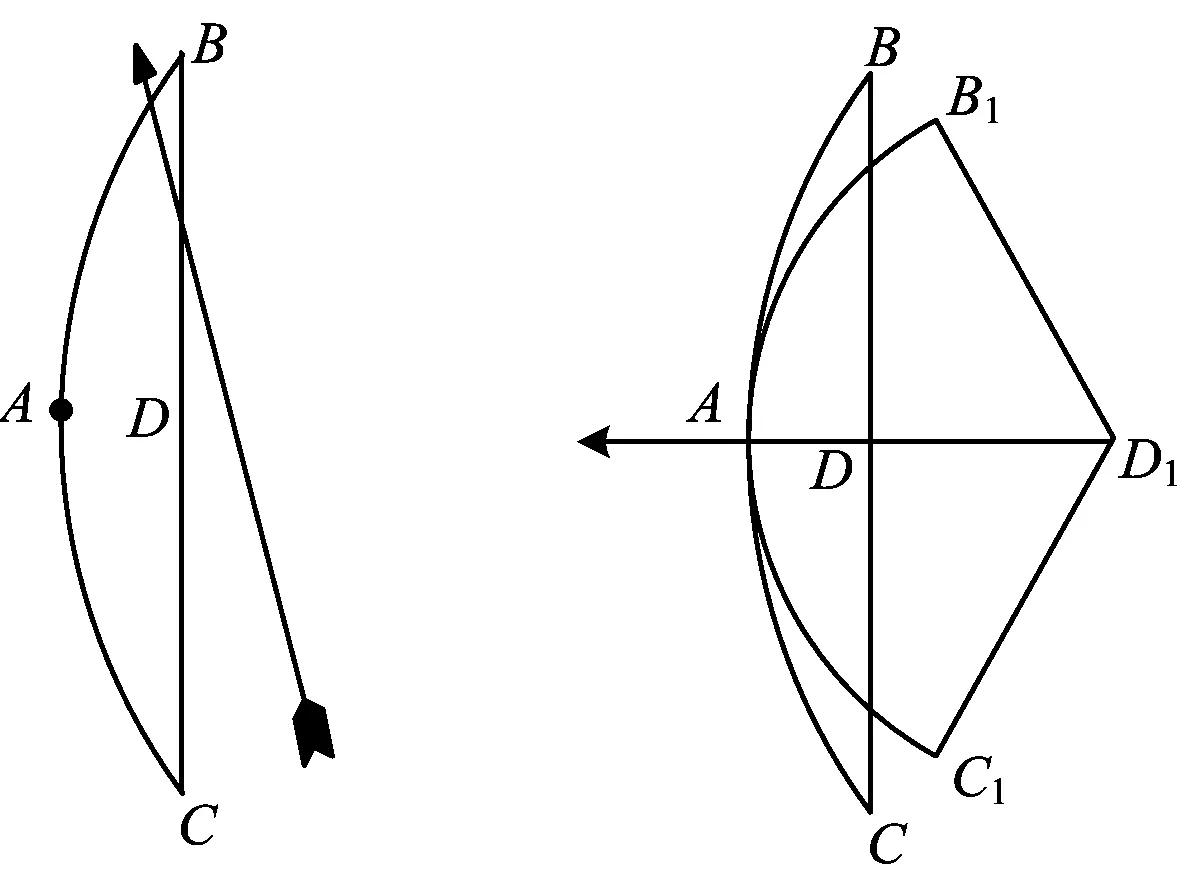
图14 图15
1)图15中,弓臂两端B1,C1的距离为______cm.
2)如图16,将弓箭继续拉到点D2,使弓臂B2AC2为半圆,则D1D2的长为______cm.

图16 图17
在本方案中,直接判断点D1是弓形所在圆的圆心,减少了通过计算的判断,把学生的探究重点放在图16中.在图17中,联结B2C2,设半圆B2AC2的半径为r,根据弧长相等,有
得到r=20,在Rt△OD2B2中,
从而
这样,在抽象出的几何图形中,通过联系圆的知识,利用垂径定理构造直角三角形等活动,将圆、直角三角形、等腰三角形以及勾股定理、圆的弧长计算、三角函数等核心知识有机地整合在一起.
在阅卷中发现,学生不理解“弓弦不伸长”,没有得出BD=B1D1=B2D2=30 cm,在图15中没有判断出D1是弓形所在圆的圆心,造成第1)小题的求解错误;在解决第2)小题时,由于学生不理解“弓臂BAC始终保持圆弧形”,就难以利用弧长相等这一等量关系得出关于r的方程.
另外,图15中两种拉弓状态、图16中3种拉弓状态分别在同一图中呈现,其好处是能够让学生直观感受3种拉弓状态之间的联系以及变化过程,但图形呈现略显复杂,且淡化了对学生空间想象能力的考查,可以将图16中箭拉到D1位置(即图中弓B1AC1)去掉,让学生在问题解决过程中,需要想象或画出该状态,更好地实现对核心素养的考查.
4 命题反思
该试题的编制过程采用“选择生活情景,抽象数学模型,进行适度整合,探究考查方向”的方法,通过不断尝试,形成试题.这给编制含有PISA理念的数学试题带来很多启发.
4.1 选择问题情境
PISA类试题都会设置一个贴近现实、蕴含数学知识的情境,且有“个人的”“社会的”“职业的”或“科学的”背景标签,与生活紧密相连,目的是让学生感受到数学的亲切,增加对问题的熟悉和理解,来考查把握有用信息的能力.本题的“弯弓射箭”,为学生所熟悉,设问方向联系实际需求,从初稿求弓臂BAC所在圆的半径,方案2求弓臂BAC的长度,方案3切线的判定,最后修改为拉弓弦的距离D1D2的长度,更接近生活实际.试图让学生在阅读的过程中,发现情境背后的数学问题本质,建模并抽象出数学问题,尝试选择恰当的数学知识解决问题,关注了空间图形与生活的结合,体现数学是有用的.
4.2 表达图形变化
4.3 体现数学思维