含裂纹球罐有限元分析及应力强度因子求解

吴林军

（福建省锅炉压力容器检验研究院，福建 福州 350008）

1 引言

球罐作为一种化工设备，与相同容积的其他储存容器相比，具有受力良好、结构稳定等优点，已广泛应用于石油化工、城建交通、航天航空、船舶和核工业等领域。然而球罐在设计、制造、组焊等过程中难免存在各类缺陷，同时其物料多为易燃、易爆和有毒介质，一旦发生事故，往往会引起灾难性的后果。缺陷种类又以裂纹的危险性最大，根据断裂力学，裂纹是否会扩展主要取决于裂纹尖端的应力强度因子KI，若KI小于材料的断裂韧性KIC，则构件能够继续安全使用，否则就必须对构件裂纹进行消除[1-3]。文中利用ABAQUS有限元软件分别分析了裂纹在不同工况下应力分布并计算其应力强度因子，为缺陷安全评定提供依据。

2 裂纹模型建立

2.1 裂纹尖端奇异性处

在弹性力学中，裂纹尖端附近应力场可由含1/r项的式子表示：

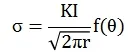
式中，r和θ为求σ值所在点的圆柱形极坐标；f(θ)为无量纲参数。当r→0，θ→0时，裂纹尖端附近点的应力将趋于无穷大，称为应力的奇异性[4]。然而这种情况实际并不存在，当应力达到材料的屈服极限时，裂纹尖端便会发生塑性变形从而使应力得到松弛，同时形成一个微小的塑性区域。如何在模型中体现裂纹尖端的应力奇异性是模拟难点。国内外学者如Barsoum、Henshell[5]等在研究过程中发现，把二阶裂纹尖端附近的奇异单元中节点移动到距离裂纹尖端1/4（B点）处时，就可以满足裂纹尖端奇异场的要求，如图1所示。

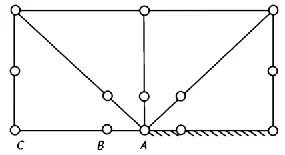
图1 裂纹尖端奇异单元

2.2 裂纹模型建立

文中在ABAQUS/CAE模块采用实体建模方法，球罐采用3D可变形实体，裂纹面采用3D可变形壳单元，模型如图2所示。球罐材料选用Q345R，弹性模量为210GPa，泊松比为0.3。分别在球罐内壁施加不同压力载荷并提取壁厚内部应力，结果如表1所示。ABAQUS采用节点应力法计算应力场强度因子，这要求裂纹尖端区域网格要划分很细。通过切取球罐含裂纹体，将壁厚内部应力作为边界条件并对裂纹尖端网格进行细化来提高计算精度，网格划分如图3所示。

表1 球罐不同内壁压力壳体应力分布

图2 球罐有限元模型

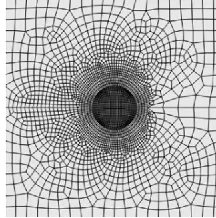
图3 裂纹体网格划分

3 表面裂纹应力分析

分别建立深2mm、5mm、8mm的表面裂纹，研究裂纹深度对球壳板应力的影响，有限元裂纹模型如图4所示。

图4 不同表面裂纹深度裂纹模型

裂纹尖端应力分析结果如图5所示，只有裂纹尖端处于塑性变形阶段，而其他部分仍处于线弹性阶段，裂纹尖端应力远大于其他部分应力，存在明显应力集中。不同压力及裂纹长度应力分布规律如图6所示。压力和裂纹深度均对尖端应力有较大影响，随着压力和深度的增加裂纹尖端应力不断增大，呈线性关系。

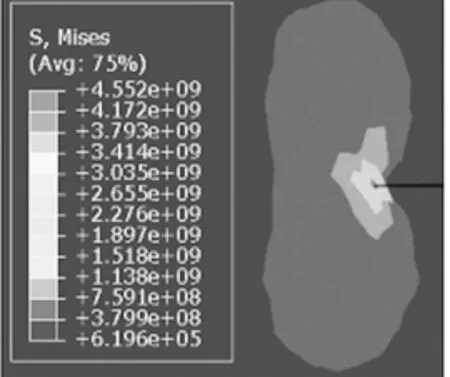
图5 裂纹尖端应力分布图

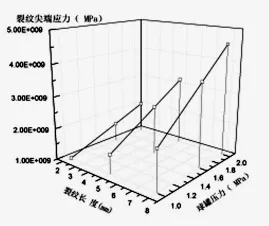
图6 不同压力及裂纹长度应力分布规律

断裂力学中反映裂纹尖端弹性应力场强弱的物理量称为裂纹尖端应力场强度因子，简称应力强度因子（Stress Intensity factor）。对于Ⅰ型裂纹，其应力强度因子的一般表达式：

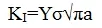
应力强度因子与裂纹尺寸a和含裂纹构件所售载荷σ成正比，是裂纹端部区域应力场的一个公共因子。它是决定裂纹端部区域应力、应变场强度的因素。对于线弹性体来说，应力强度因子与载荷呈线性关系，并取决于物体与裂纹的几何形状和尺寸。不同压力和裂纹长度下应力强度因子分布规律如图7所示，与表达式一致，当裂纹体受载增大或裂纹长度增大时，裂纹尖端附近的应力强度因子KI随之增大。

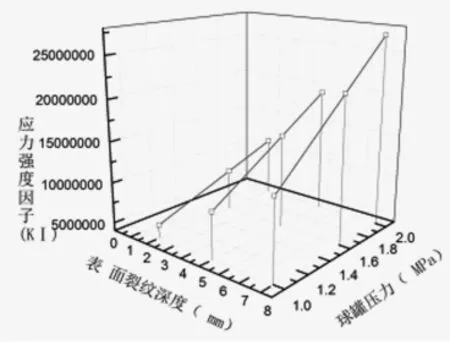
图7 表面裂纹应力强度因子分布规律

4 埋藏裂纹应力分析

通过建立深2mm、5mm、8mm长置于板厚中心的埋藏裂纹，研究埋藏裂纹长度对球壳板应力的影响并与尺寸表面裂纹比较，分析其危害性。中心埋藏裂纹应力分析如图8所示。从图中可以看出裂纹尖端应力分布呈现“蝴蝶”形貌。受裂纹自由面影响，裂纹平面法向两侧形成“水滴形”低应力场区。应力最大值位于裂纹端部并随着压力和长度的增大而增大。不同压力下不同中心埋藏裂纹长度球壳板应力规律如图9所示。从图中可以看出，与表面裂纹应力分布规律相同，裂纹应力同样随着压力和长度增大而增大。同样压力和裂纹长度下，表面裂纹尖端应力要比埋藏裂纹尖端应力高出一个数量值，危害性要比埋藏裂纹高得多。

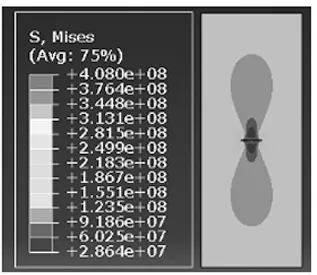
图8 中心埋藏裂纹应力分布

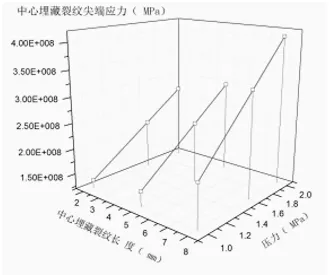
图9 不同压力及裂纹长度应力分布规律

中心埋藏裂纹应力强度因子与压力、裂纹长度关系如图10所示。与表面裂纹相同，KI随着压力和裂纹长度变大而变大，但应力强度因子值要比表面裂纹小得多，同样外界条件下，表面裂纹先扩展。

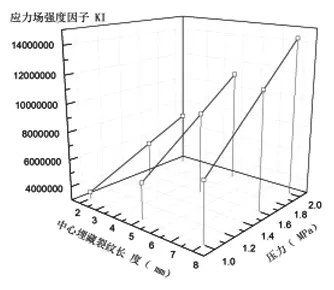
图10 中心埋藏裂纹应力强度因子分布规律

为进一步研究埋藏裂纹位置对应力的影响，以8mm裂纹长为例分析应力变化规律，简化模型如图11所示。球罐工作压力为1.6MPa下，不同偏离长度裂纹应力分析如图12所示。随着裂纹往板中心偏离，尖端应力越来越小。裂纹两尖端应力分析对比如图13所示，同样压力下A点应力明显高于B点。裂纹两尖端应力场强度因子分析对比如图14所示。越靠近板中心应力场强度因子越小，且距离表面越近，应力场强度因子的值下降得越快。

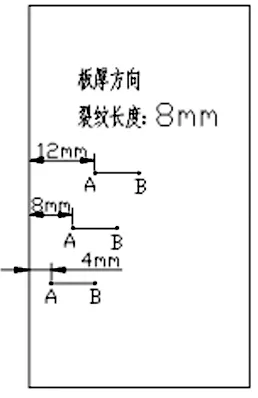
图11 不同裂纹位置简化模型

图12 不同偏离长度应力分析云图

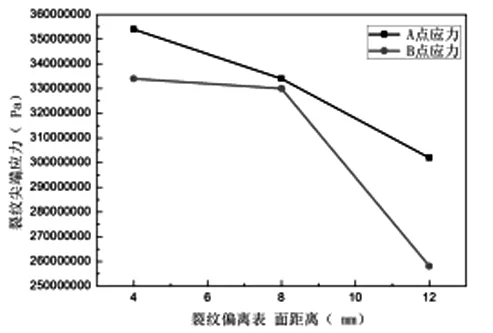
图13 裂纹两尖端应力对比

图14 裂纹两尖端应力场强度因子对比

5 结论

（1）将裂纹植入有限元模型，并对裂纹尖端网格细化提高计算精度，分析裂纹长度、受力情况等对裂纹应力分布的影响。结果表明，裂纹尖端存在很大应力集中，尖端应力值随着裂纹长度增大而增大。同样载荷参数下，表面裂纹尖端应力比埋藏裂纹高，危害性较大。

（2）在ABAQUS中采用节点应力法分别计算表面裂纹和埋藏裂纹应力场强度因子。结果表明，同样外部条件，表面裂纹应力场强度因子值比埋藏裂纹高出一个数量级。相比埋藏裂纹，表面裂纹优先扩展。

（3）研究埋藏裂纹不同位置对应力分布影响。结果表明，随着裂纹往板中心偏离，尖端应力越来越小，应力场强度因子也越来越小。