基于多因素信息融合的城市供水安全评价系统*

2018-11-30刘朝峰

中国安全生产科学技术 2018年11期

王威，刘畅，刘朝峰

(1.北京工业大学抗震减灾研究所，北京 100124；2.北京工业大学建筑与城市规划学院，北京 100124；3. 河北工业大学土木与交通学院，天津 300401)

0 引言

目前，国内外研究学者提出了多种供水安全的评价方法，Caroline[1]提出利用水贫困指数对水安全进行评价；韩宇平等[2]以层次分析法(AHP)确定指标的权重,建立了物元模型评价，以河北滹滏平原为例,对水资源状况进行了综合评价；李如忠等[3]在物元分析的基础上，结合模糊理论和欧氏贴近度概念，建立了区域水安全评价的模糊物元模型，并将该模型用于中国部分省级行政区域的水安全评价；金菊良等[4]基于加速遗传算法的模糊层次分析法筛选指标、确定各指标和子系统的权重，用集对分析方法建立了基于联系数的流域水安全评价模型(CN-AM)。上述研究为开展供水安全评价提供了参考，然而在评价过程中存在着缺少定量和定性信息的综合分析、先验数据不易获得等问题。证据理论[5]作为1种不确定推理方法，需要的先验数据直观且容易获得，且Dempster合成公式可以综合不同专家或数据源的知识或数据，为多信息的融合提供了新的方法[6-9]，能够较好地在多个领域量化与融合不确定性风险因素。基于此，本文将供水安全看成多属性决策问题，提出了1种基于D-S证据理论的供水安全评价方法。

1 DS证据理论的基本概念和合成规则

1)基本概率分配函数

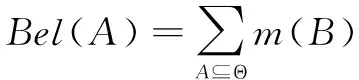
(1)

式中：m(A)>0的A称为焦元。

2)Dempster合成规则

Dempster合成规则也称证据合成公式，其定义如下：

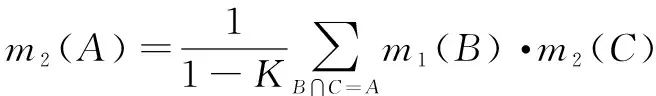
(2)

式中：K为归一化常数。

(3)

3)冲突证据融合方法

为了解决证据之间的冲突性，邓勇等[10-11]引入距离函数:

(4)

定义证据体mi和mj之间的相似度Sim(mi,mj):

Sim(mi，mj)=1-dBPA(mi，mj)，i，j=1，2，…，n，进一步求出各个证据的支持度Sup(mi)和可信度Crd(mi)。利用可信度作为权重,对收集证据的基本概率指派进行加权平均，最后使用Dempster组合规则融合加权平均证据。当系统有n个证据时，将加权平均证据组合(n-1)次。

(5)

(6)

2 建立基于多因素信息融合的供水安全评价体系

2.1 供水安全评价指标体系的建立

根据以往的研究和专家经验[12-13]建立城市供水安全评价指标体系，从供水过程的供水水源状况、输水状况、用户用水状况、净水状况4个环节选取12个评价指标，如表1所示。

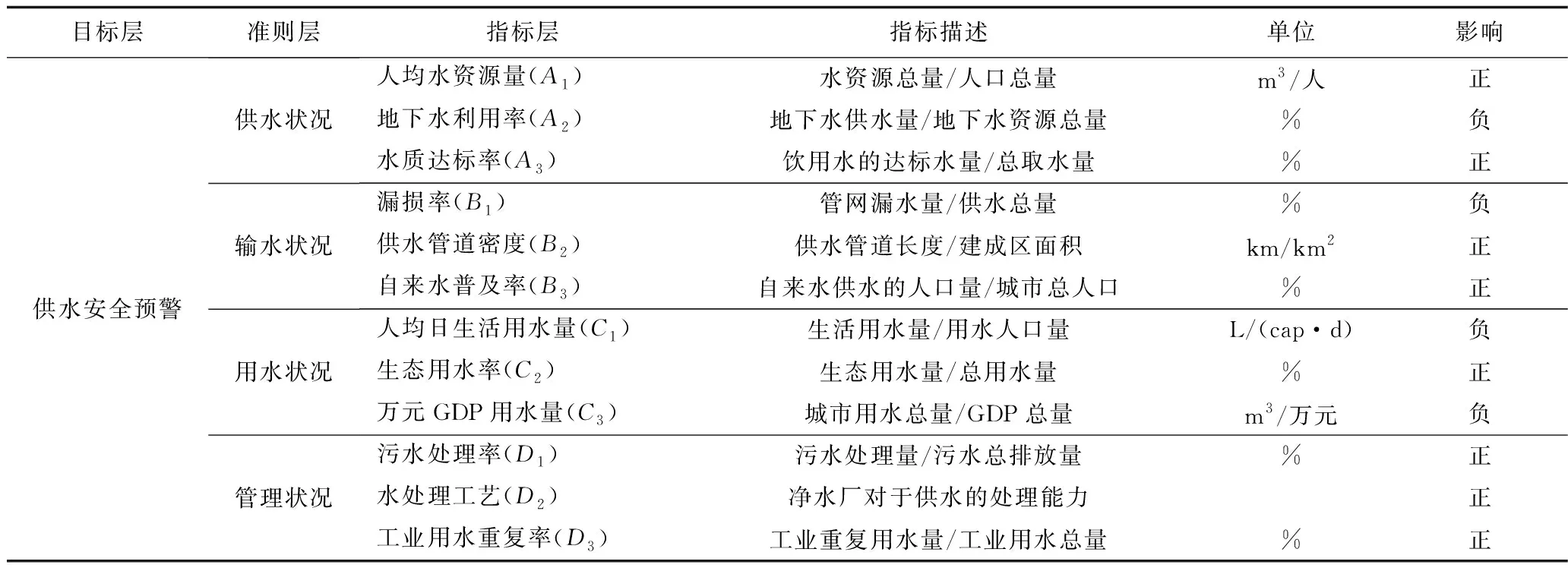
表1 城市供水安全指标体系Table 1 The indicators system for urban water supply security

2.2 指标组合权重确定

1)主观权重ωz

层次分析法[14](AHP)是确定主观权重的一种常见方法，利用AHP法得到指标权重ωz。

2)客观权重ωk

运用熵权法计算指标的客观权重ωk。熵值：

(7)

由熵值确定指标熵权：

(8)

3)最优组合权重ω[15]

建立目标函数F使得最优组合权重ω接近ωz与ωk：

(9)

利用Lagrange乘子法求解后得到：

(10)

根据式(10)可得到评价指标的组合权重值。

2.3 安全等级划分标准

将供水安全等级划分为5个等级，如表2所示。Ⅰ级表示系统很安全，此时城市供水各方面都达到良好的水平，处于持续安全的状态；Ⅱ级表示系统比较安全；Ⅲ级表示系统基本安全，但需要对供水各方面的安全加以注意，预防系统安全状态恶化；Ⅳ级表示系统较不安全，应当立即寻找警源，采取措施，使系统恢复到安全状态；Ⅴ级表示此时系统非常不安全，必须马上找到警源，采取紧急措施，保障供水系统的安全性。根据国家相关部门的标准以及国内外对于指标临界值的研究，形成安全指标等级的评价标准，如表3所示。

表2 安全等级划分Table 2 Classification of safety

2.4 基本概率分配函数(BPA)生成及其融合方法

1)基本概率分配函数BPA

将城市供水安全评价体系作为1个识别框架，结合安全等级的划分，为了表示5个不同的安全等级，选取a，b，c3个元素为基本概率分配函数(BPA)的焦元元素[16]，Ⅰ～Ⅴ级安全等级的基本概率分配函数焦元分别是m(a)，m(ab)，m(b)，m(bc)，m(c)。

2)加权合成的BPA函数

冲突证据之间的融合方法大致可以归结为2大类：第1类方法主要是改进Dempster组合规则，第2类方法认为Dempster组合规则没错，应该先对冲突的BPA进行预处理。本文采用第2类方法的观点，首先对冲突证据(BPA函数)进行加权处理，以权重系数作为证据的支持度，获得各指标的加权BPA函数值，再利用传统融合规律进行计算。

表3 供水安全指标等级的评价标准Table 3 Evaluation criteria for water supply safety indicators

3 实例应用

通过年鉴数据调研，本文以2006—2016年郑州市的供水安全数据为基础数据(见表4)进行案例分析。

根据表4中的供水安全指标的数据以及表2中的安全等级划分标准，将2006—2016年郑州市供水安全系统中的每一指标都作为1个证据，得到相对性的概率分配函数焦元。

根据式(10)中的组合权重值计算方法，得到城市供水安全评估指标的最优组合权重ω=[0.130，0.060，0.177，0.074，0.058，0.030，0.100，0.075，0.044，0.045，0.151，0.056]。以2006年为例：m(a)=0.030+0.100+0.056=0.186；m(b)=0.058+0.075+0.151=0.284；m(c)= 0.177+0.045=0.222；m(ab)=0.000；m(bc)=0.130+0.060+0.074+0.044=0.308。得到其他年份各指标数据的加权合成基本概率分配函数如表5所示，利用DS合成规律进行11次融合后结果如表6所示。与运用邓勇提出的冲突证据融合方法得到的结果对比，发现两者结果大致相同，确定的主焦元完全一致，也证明了本文方法在处理具有冲突性证据融合的有效性，且在计算过程中发现本文方法有更快的收敛速度，提高了证据融合的可靠性。

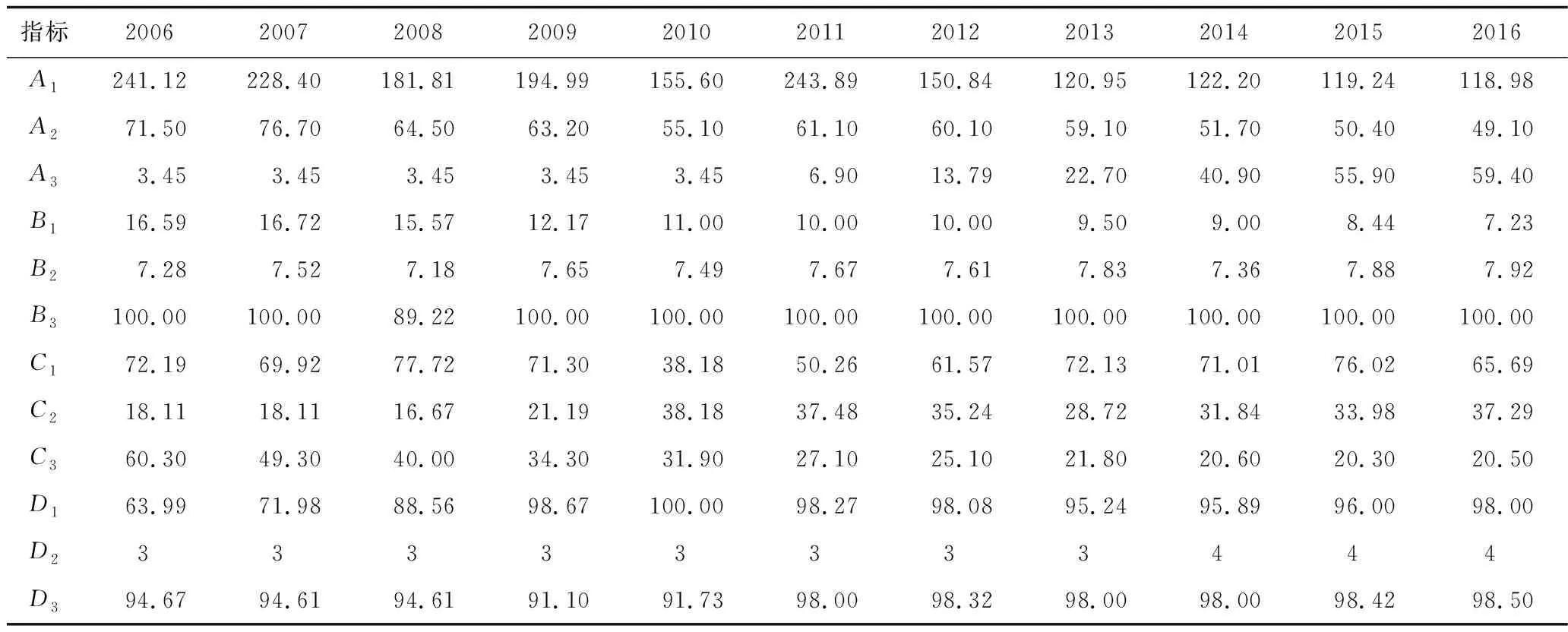
表4 2006—2016年郑州市供水安全指标数据Table 4 Water supply safety indicators for Zhengzhou city from 2006 to 2016

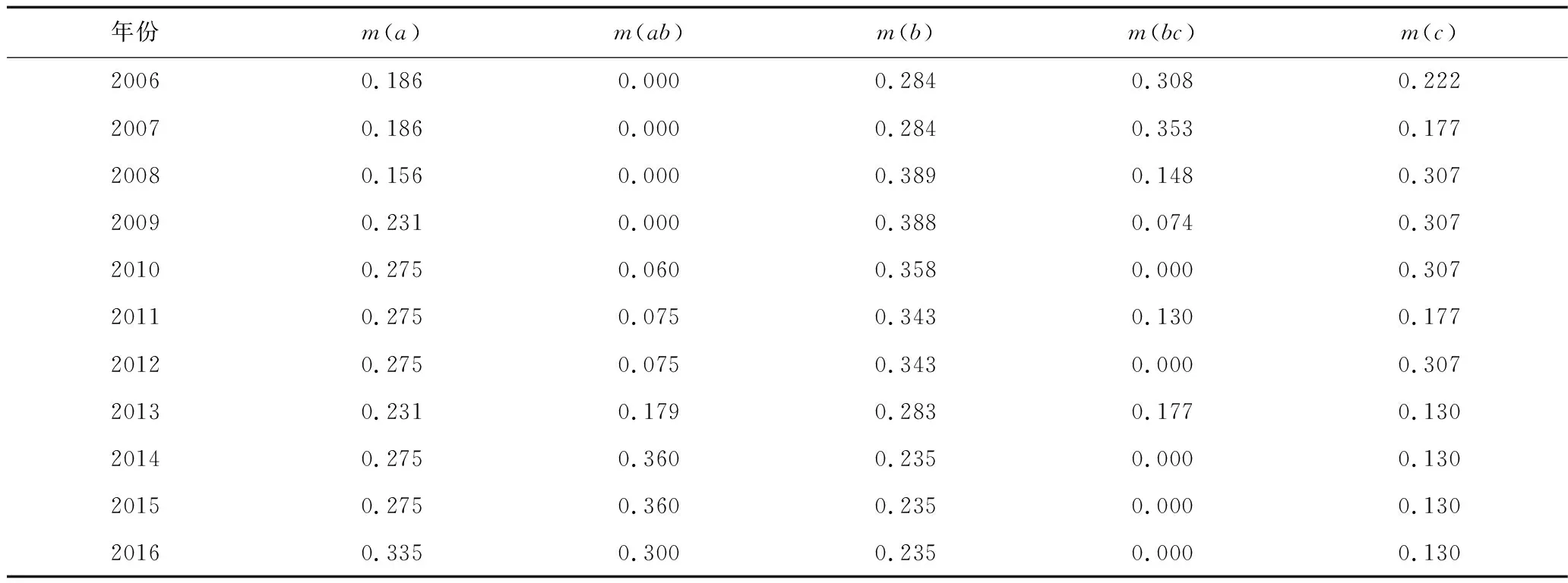
表5 2006—2016年各指标数据的加权合成基本概率分配函数Table 5 Weighted synthesis of basic data for each indicator data from 2006 to 2016

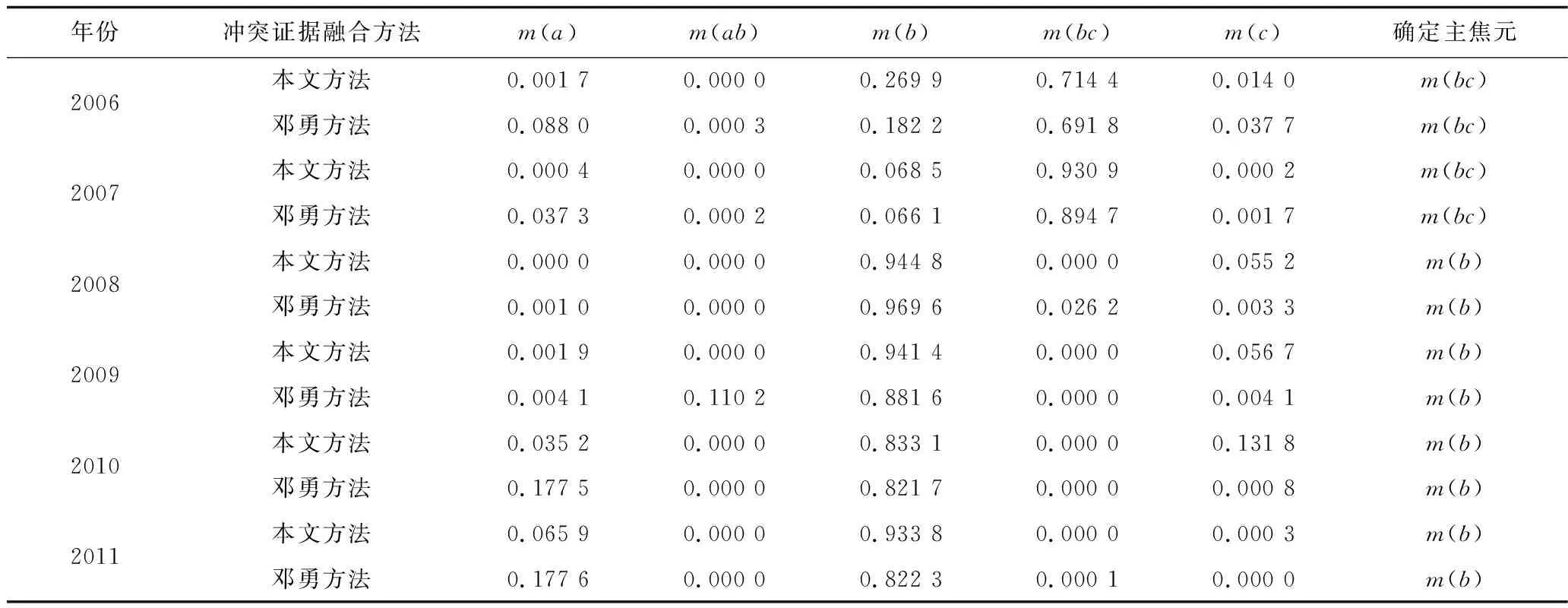
表6 供水安全多证据指标融合后的结果及对比Table 6 Results of water security safety multiple evidence fusion

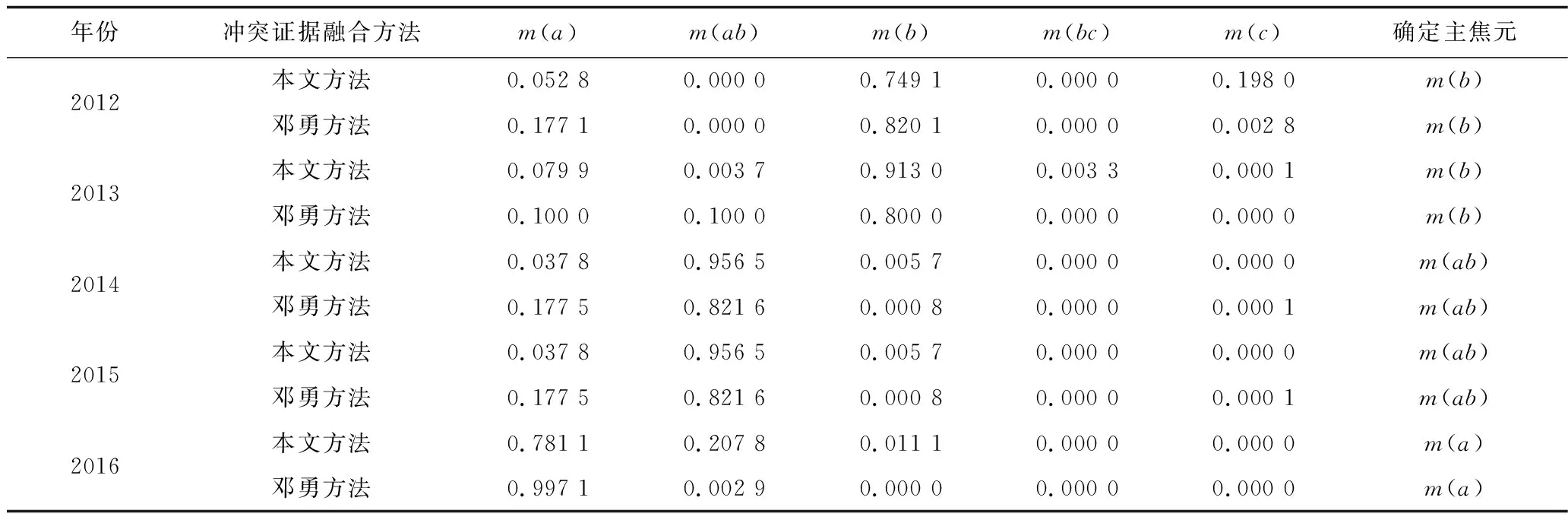
表6(续)

表7为2006—2016年供水安全级别的计算结果，将得到的结果与采用可拓物元分析法[3]得到的结果对比，发现两者的趋势基本相同，验证了本文方法在判断供水安全等级的可行性和实用性。

表7 2006—2016供水安全级别计算结果Table 7 Water safety alarm level calculation results from 2006 to 2016

本文以安全等级3级作为分析评价结果的基准，从表中可以看出2006—2016年郑州市的供水安全等级是逐渐升高的，2006与2007年的安全等级偏低，2008年以后安全等级逐渐回升并且趋于稳定状态，可以预测出在未来一段时间郑州市的供水安全等级将保持在较高的水平，供水处于安全状态。

为了便于分析造成供水不安全的原因，利用同样的方法计算得到准则层的各指标安全等级，结果如图1和表8所示。

从表8以及图1分析出现情况的原因，供水水源安全层面上，安全等级数值在Ⅲ～Ⅳ间浮动，表明郑州市的水资源量仍然是处于缺少状态，水质问题也存在不足，整体处在较高的安全等级，充分表明了水源是制约着城市供水安全的重要因素，所以南水北调工程十分的必要。输水和净水安全层面上，安全等级数值呈现下降的稳定趋势，表明在输水和净水方面，政府采取了正确的防范措施，减少了供水不安全事件的发生。用水安全层面上，可以发现安全等级出现了大的波动，从相关资料中发现了郑州市政府创立了节水部门，大力推进居民节水意识，使得用水效率大大提高，但在2010年之后随着大量外来人口的增加和城市的快速发展，城市用水与快速增长的人口数量无法相适应，用水方面的安全等级又发生了提高。