城市规模对能源消耗的空间溢出效应

刘 帅,董会忠,刘明睿,唐 磊

(山东理工大学 a.经济学院;b.管理学院，山东 淄博 255012)

1 文献综述

随着经济社会的发展,我国城市化率不断提升,城市规模扩大引起的能源消耗问题日益凸显。英国石油公司(BP)统计显示,2010年我国能源消耗总量第一次超越美国,成为世界第一大能源消耗国。但随着我国城市化水平的不断提高,未来一段时间内城市规模仍将不断扩大,城市能源消耗量还将持续增加,能源资源短缺和化石能源消费带来的社会问题将更加突出。控制城市能源消耗量、降低CO2等温室气体排放成为国内外学者关注的焦点问题。

目前,国内外学者对城市与能源消耗的研究主要集中在城市化水平和城市结构对能源消耗的影响。①城市化水平提升与工业化程度存在密切关系。Jones D W通过控制工业化程度研究发展中国家城市化率对能源消耗的影响,发现城市交通是增加城市能源消耗的主要因素,指出发展中国家人均能源消耗对人均收入的弹性系数为0.35—0.48[1]。Jones D W研究提出的潜在假设是发展中国家工业化程度不变、城市交通以化石燃料为主，但我国城市化水平在迅速发展的同时，工业化程度有了显著提升,电力交通成为城市主要的公共交通工具,城市化、工业化与能源消耗的关系发生了很大变化。基于此,王蕾、魏后凯重新研究了我国城镇化、工业化与能源消耗的关系,认为我国城镇化和工业化对能源消耗存在正向溢出效应[2]。②城市化水平提升通过影响产业结构和城镇居民消费水平间接影响能源消耗。严翔等基于Kaya拓展模型研究了1998—2015年我国城市产业、空间与人口交互发展对能源消耗的影响,指出城镇化对生产端能耗的影响大于生活端,但居民消费支出仍是能源消耗的间接提升因素[3]。此外,何晓萍利用面板数据非线性模型和协整模型研究了我国城市化水平与电力消耗的关系[4];许泱等采用我国30个省际面板数据检验了碳排放与城市化水平的关系,发现城市化水平与能源消耗呈正相关,指出城市化水平与能源消耗之间不存在环境库兹涅茨曲线[5];黄飞雪等运用STR模型研究了城市化水平与能源消耗的关系,发现我国城市化水平与能源消耗存在非线性关系[6]。

从城市化水平角度研究往往会忽视城市内部建设对能源消耗的影响机理,因此有学者从城市结构和城市人口密度两个角度研究城市与能源消耗的关系。Orit Mindali等在分析城市空间结构时指出城市规模越大,人均能源消耗越低[7];程开明在利用我国286个城市面板数据研究城市建设紧凑度与能源消耗关系时发现,城市紧凑度与能源消耗呈负相关,城市紧凑度越高越有利于节能减排[8];范进通过构建经济学模型研究城市人均交通能耗、家庭能耗与城市人口密度之间的关系,指出现阶段我国城市人口低密度会激发居民对能源的消费,不利于节能减排[9]。从城市人口密度对能源消耗影响的研究可见,学者们将城市人口看作一个整体进行研究,这对小规模城市的效果可能会更好，而对大城市来说,经济社会活动相对复杂,从城市人口结构变化研究城市能源消耗效果会更优。因此,郭文、孙涛从城市人口年龄结构、教育结构和职业结构研究了人口结构对能源消耗的影响,指出现阶段我国人口结构变动减缓了能源消耗的增长速度[10]。

随着城市化进程的推进和城市规模的不断扩大,学者们开始关注城市规模对能源消耗的影响。Richard York在对14个欧盟国家城市人口规模与能源消耗关系的研究中指出,城市人口规模扩大会降低人均能源消耗[11];Usama Al-mulali等用完全修正普通最小二乘法研究了东亚、东欧等国家和地区的城市规模与能源消耗间关系,发现84%的国家和地区的城市规模与能源消耗呈长期的正相关,其他国家和地区城市规模与能源消耗呈长期的负相关[12];许抄军等研究发现,我国城市规模与能源消耗呈正“N”型关系[13];Yimin Chen等通过GIS遥感技术研究了珠江三角洲5个城市的城市规模与能源消耗关系,指出城市规模与能源消耗呈正相关,城市建设紧凑度与能源消耗呈负相关[14];Qiang Wang用时间序列数据研究了我国城市规模对生产能耗和住宅能耗的影响,发现经济规模与能源消耗成正比,科技进步与能源消耗成反比[15];陈龙等通过SFA模型从城市能源效率方面研究城市规模对能源效率的影响,得出城市规模越大,能源效率越高,但两者存在非线性关系[16]。

从现有文献看,研究者对城市与能源消耗的研究是将城市作为一个单独的个体,这与现实中各城市密切联系的事实相悖,特别是城市群的建设使城市间的关系更加密切。忽视城市空间联系研究城市规模与能源消耗的关系容易导致误判，因此本文将时空权重矩阵引入到城市规模对能源消耗影响的计量模型中,研究城市规模对能源消耗的影响,消除忽视空间因素而导致的估计偏差,以更客观地解释城市规模与能源消耗的关系,为相关部门制定城市发展政策和能源消耗控制措施提供决策支持。

2 研究方法与数据来源

2.1 研究方法

STIRPAT模型:Ehrlich、Holden首次提出建立了“IPAT”模型,研究人口、财富、技术对环境的影响:

I=PAT

(1)

式中,I为环境压力;P为人口数量;A为富裕度;T为技术。基于IPAT模型的局限性,Dietz在IPAT模型的基础上建立了STIRPAT模型。标准形式为:

I=αPβ1Aβ2Tβ3ε

(2)

式中,α为模型的系数;β1、β2、β3分别为变量的指数;ε为随机误差。

将式(2)两边取对数得:

lnI=lnα+β1lnP+β2lnA+β3lnT+lnε

(3)

传统STIRPAT模型只是将研究单元作为独立个体进行研究,忽视了环境压力影响因素在空间上的联系，而将空间因素纳入传统计量模型研究经济社会活动会更符合现实情况。基于此,本文试图将内生时空权重矩阵纳入STIRPAT模型,分析城市规模对能源消耗的影响。

全局空间自相关:空间计量模型是在观测值具有显著的空间相关性的基础之上设定的,目前计算空间相关性的常用方法为全局Moran′s I[17]。全局Moran′s I的具体表达式为:

(4)

(5)

时空权重矩阵构建:空间权重矩阵反映的是个体或区域间的空间交互关系,城市间的相互影响会随着两城市间距离的增加而减弱,但这种影响超过某一临界值,城市间相互影响的作用会迅速下降。基于此，本文构建反距离空间权重矩阵形式为:

(6)

式中wij为空间权重;dij为两地距离;L为距离临界值。基于反距离空间权重矩阵的构建是外生的,不能考察空间溢出效应的时间转移和传导效应[18],本文在反距离空间权重基础上构建内生时空权重矩阵,以期更准确地考察城市规模对能源消耗的空间溢出效应的时间转移和传导效应。为考察空间溢出效应在时间上的转移和传导,本文采用不同时间的Moran′s I的比值构建内生时间权重矩阵。表达式为:

式中,ζnm为时间m的Moran指数与时间n的Moran指数的比值。与空间权重矩阵不同的是,时间权重矩阵上三角元素值为0,是因为前一期只对后一期存在时间溢出效应,而后一期不能影响前一期。下三角元素取值列为对应年份的空间溢出效应,行这对应年份空间溢出效应的时间影响效应[18]。根据式(6)的反距离空间权重矩阵和式(7)的时间权重矩阵,采用克罗内克积得到时空权重矩阵。表达式为:TW=ζ⊗w,⊗为克罗内克积符号。

空间杜宾模型构建:空间计量模型的选择对研究观测值间的空间关系十分重要,目前常用的空间计量模型主要有空间自回归模型(SAR)、空间误差模型(SEM)和空间杜宾模型(SDM)。LeSage指出选用SDM模型是科学研究者首先考虑的,这是因为SDM模型在数据生成过程中能得到系数的无偏估计,同时该模型没有预先对空间溢出规模设定限制,能更好的估计溢出效应[19]。SDM基本模型为:

Y=ρwY+β1X+β2wX+ε

(8)

为检验SDM模型是否适用于观测数据,一般采用LM检验,假设条件有两个:①H0:β2=0;②H0:β2+ρβ1=0。假设条件①可将空间杜宾模型简化为空间自回归模型:Y=ρwY+βX+ε;假设条件②可将空间杜宾模型简化为空间误差模型:Y=βX+ε,ε=λwε+μ。通过假设检验条件可见,SDM模型是SAR模型和SEM模型的一般形式。

将式(3)与式(8)结合,并引入时空权重矩阵,最终考察城市规模对能源消耗的空间溢出效应的计量模型为:

lnI=ρTWlnI+β1lnP+β2lnA+β3lnT+β4lneco+β5sec+α1TWlnP+α2TWlnA+α3TWlnT+α4TWlneco+α5TWsec+ε

(9)

式中,I为人均能源消耗;P为年末城市总人口,表示城市规模;A为人均GDP,表示人口富裕度;T为年末科技从业人员;eco为经济密度即城市GDP与城市面积比值;sec为第二产业占GDP比值表示产业结构。

直接效应与间接效应:SDM模型中解释变量的系数值并不能准确的反映对城市能源消耗的影响,针对这一问题,LeSage、Pace[19]提出了偏微分方法对空间效应进行分解测算。

对空间杜宾模型式(8)进行变化可得:

(In-ρW)Y=(Inβ1+β2W)X+lnα+ε

(10)

令,V(W)=(In-ρW)-1,Sr(W)=V(W)(Inβ1r+Wβ2r),则式(10)可转化为:

(11)

+V(W)(tna+ε)

2.2 数据来源

本文的研究样本为我国地级及以上城市，全部数据来源于2006—2015年的《中国城市统计年鉴》。由于部分城市是2006年以后设市,统计数据不完整，另有部分城市(如拉萨)统计数据严重缺失,因此在选择样本城市时将上述两种城市剔除,最终保留285个样本城市。对与样本城市个别数据缺失的则通过查找相应的地方统计年鉴予以补齐。

各市能源消耗总量计算公式:

TI=ΣEi×ηi

(13)

式中,TI表示各市能源消耗总量;Ei表示第i类能源消的耗总量;ηi表示第i类能源折算成标准煤的折算系数。各类能源与标准煤的具体折算系数见表1。

表1 各类能源折算系数

3 实证分析

3.1 城市能源消耗空间性分析

借助ArcGIS 10.2软件的空间趋势分析工具,选取2006年、2009年、2012年和2015年人均能源消耗量作为Z值,X、Y值分别为东西、南北方向生成三维趋势图(图1),以揭示我国城市能源消耗的空间格局变化。

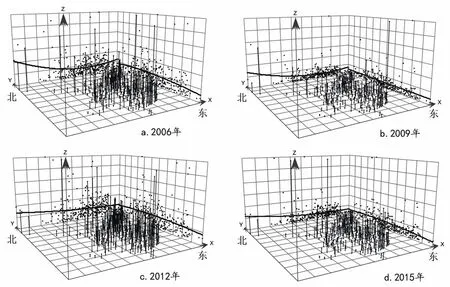
图1 城市能源消耗空间格局变化趋势

由图1可见,2006年城市能源消耗空间投影在东西方向上呈自西向东的下降趋势,在南北方向上呈自北向南的下降趋势,但东西方向下降幅度大于南北方向,说明这段时间城市能源消耗空间差异较大。2009年,空间投影自西向东下仍呈下降趋势,但下降幅度变小,表明东西方向城市能源消耗差异变小,南北方向投影曲线较为平滑,但人均能源消耗量均值上升为0.789。2012年,城市能源消耗在东西、南北方向上的趋势线相较于前几年更为平滑,但能源消耗均值继续上升,达到0.911。研究末期,城市能源消耗呈由西向东的平缓下降趋势,南北方向趋势平滑,人均能源消耗上升为1.028,表明我国城市能源消耗整体上升的同时,区域差异在逐渐缩小,但东西差异仍然大于南北差异。

根据式(4)计算历年人均能源消耗全局空间自相关指数,见表2。由表2结果分析,我国城市能源消耗全局Moran′s I显著为正,说明城市能源消耗存在正向空间依赖关系,同时表明引入空间计量模型研究城市规模对能源消耗的影响,可以消除由空间相关性引起的回归偏误。

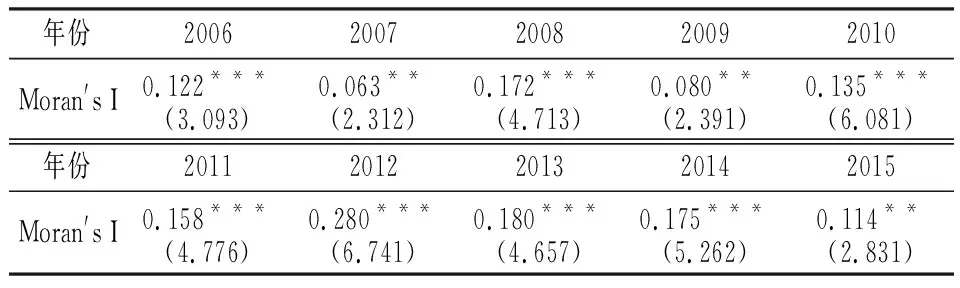
表2 人均能源消耗全局自相关Moran′s I指数

注:表中*、**、***分别为10%、5%、1%水平上显著(下表同)；括号内数值为Z检验值。

3.2 空间计量模型检验与结果讨论

在估计空间面板数据模型时,本文首先采用Hausman检验判断模型的固定效应和随机效应。在不考虑空间相关性条件下，Hausman的检验结果为χ2=87.53,在1%的显著性水平上拒绝原假设,即选择固定效应模型来拟合数据会更优。估计结果表明,反距离空间权重下的空间模型估计结果并不显著,城市规模对能源消耗的空间溢出效应存在距离门限。即在某一距离半径内城市规模对能源消耗的影响会随着距离的增加而减弱,超出这一半径将不存在空间影响。对比不同距离半径下SDM模型的拟合优度确定最佳距离半径范围为200—400km。为准确测算空间溢出半径,在200—400km范围区间内每隔20km进行一次空间模型回归,运行结果见表3。

表3 不同距离下SDM拟合优度

表3为不同距离阈值下SDM模型的拟合优度和最大似然估计值结果,通过对比结果发现距离阈值在340km、360km时拟合优度达到最大值,因此采用340km和360km的算数平均数350km作为距离阈值。同时，将350km带入空间回归模型中发现拟合优度达到最大值0.8905,因此选用350km作为距离阈值研究城市规模对能源消耗的空间溢出效应最佳。以350km距离阈值建立反距离空间权重矩阵,不同模型下的估计结果见表4。

对比表4中4种模型的拟合优度和最大似然估计量,空间计量模型的拟合优度均在85%以上,高于普通面板数据回归拟合优度,可见空间计量模型的拟合效果更好。Log-likelihood为似然函数值的自然对数,此值越小模型拟合程度越好。综合考察这两项指标,可知选择SDM模型效果最佳。从表4可知,SDM模型的空间滞后项参数显著为正,与前述全局空间自相关指数属性一致,反映了某一地区能源消耗会受周边地区影响。从系数结果看城市人口规模扩大对城市能源消耗产生负向影响,人口富裕度、产业结构变化对城市能源消耗的影响显著为正,表明人口富裕度和工业产业发展会促进城市能源消耗。从解释变量的空间溢出效应分析,人口数量对城市能源消耗影响显著为正。即城市人口规模扩大在抑制本地区能源消耗的同时会促进周边地区城市能源消耗;经济密度和第二产业比重的参数估计显著为负,表明两者在促进本市能源消耗的同时会抑制周边城市的能源消耗。上述三种因素可看作是城市间能源消耗分化的主要推动力。城市人口富裕度对周边城市能源消耗溢出效应为正,表明当前城市人口富裕度是推动能源消耗的主要因素。

表4 空间模型回归结果

注:括号内数值为t值结果,“—”表示此项为空。

从表5可知,城市人口对本地城市能源消耗的影响显著为负,对其他城市的空间溢出效应为正,且总效应为正。城市人口富裕度的直接效应、间接效应和总效应均显著为正,表明城市人口是城市能源消耗的主要因素。城市科技进步只对本地能源消耗存在正向影响,间接效应和总效应不显著。城市经济密度和工业比重对本市能源消耗存在正向影响,且空间溢出效应显著为正。从全国范围来看，影响城市能源消耗增加的主要因素是城市人口和人口富裕度,工业发展反而会抑制能源消耗。为探究时间传导效应对城市规模与能源消耗空间溢出效应的影响,根据式(9)的计算结果见表6。

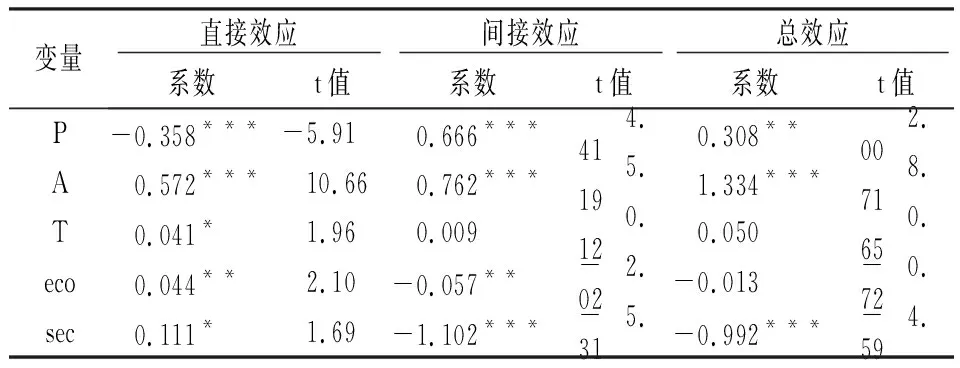
表5 城市规模对能源消耗空间效应分解

表6 SDM模型下采用时空权重矩阵参数效应分解结果

表7 分地区城市规模对能源消耗空间效应分解

城市能源消耗的时间传导效应体现在不同时期能源消耗的空间自相关指数比值上,这一效应会影响城市规模对能源消耗的空间溢出效应。表6综合了城市规模对能源消耗的空间溢出和时间传导效应,两者共同作用于城市能源消耗。在这一影响下考察各变量的作用,城市人口、人口富裕度、城市科技、城市经济密度和第二产业占比每提升1%,引起城市能源消耗的变动分别为-1.045%、0.352%、0.679%、0.193%、0.234%。

对全国平均而言,城市规模对城市能源消耗存在显著的空间溢出效应,但由于各城市初始发展水平和早期国家战略政策存在很大差异。对不同地区的城市规模是否对能源消耗存在空间溢出效应,对该问题的探讨将有助于从另一个角度理解城市规模对能源消耗的影响机制。因此,将城市样本按东部、中部、西部进行分组比较,考察城市规模异质对能源消耗的影响，结果见表7。

表7考查了不同地区城市规模对能源消耗的空间溢出效应。结果显示:①东部与中部地区城市规模对城市能源消耗的直接效应显著为负,西部地区直接效应为正;中部和西部地区对能源消耗的总效应在1%的水平上显著为负,而东部地区的负向总效应不显著。原因在于:东部地区城市化水平相对较高、城市内部结构相对完善,城市公共交通是城市人口通勤的基本工具,人口数量增加会降低交通设施的空载率,从而降低城市人口能源边际消耗率。东部地区经济相对发达,城市吸引人才能力强,城市人口受教育水平相对较高,人们节能减排意识高于中西部地区。②全国范围内,城市富裕度对本地能源消耗的直接效应在1%的水平上显著为正。随着城市居民收入水平的提高,为改善拥挤的公共交通条件而更多地选择私家车,这一选择直接提高了城市能源消耗。但城市富裕度对城市经济发展较高的东部地区总效应为负,而对中部地区总效应为正,这说明了环境库兹涅茨曲线的存在。③城市经济密度和第二产业发展水平对本地区能源消耗的影响显著为正,这一影响在东部和中部区更明显,表明我国东部、中部城市经济快速发展是建立在高能耗基础上的。但在东部和中部地区,第二产业比重对城市能源消耗总效应为负,这得益于各地区制造业升级带来的良好反应。

4 结论与建议

本文在利用STIRPAT模型估计城市规模对能源消耗影响的基础上,引入空间权重矩阵和时空权重矩阵,考察城市规模对能源消耗空间溢出效应并探究了空间溢出效应的时间传导效应。本文发现:①城市规模对能源消耗的溢出半径为350km,当超过这一阈值后,空间溢出效应会迅速减少直至消失。②城市规模对能源消耗的空间溢出效益为异质。从直接效应看,能源消耗的最大影响因素东部地区是城市经济密度,中部地区为科技水平,西部地区为城市富裕度;从总效应看,东部城市能源消耗的最大影响因素为经济密度,中部地区是城市富裕度,西部地区是第二产比重。城市人口数量在全国范围内对能源消耗的空间效应是一致的,城市人口数量增加均会抑制城市能源消耗。③城市富裕度对城市源消耗影响的差异证明了环境库兹涅茨曲线的存在。

基于上述研究结论,本文提出以下建议:①城市能源消耗有很强的空间自相关性,并具有明显的空间溢出半径,各城市应加强与周边城市的联系。同一区域城市可以通过人才共享、产业互补的政策密切与周边城市的关系,形成独具特色的城市协同发展模式,在制定节能减排政策时要综合考虑周边城市,共同防治,以免事倍功半。②根据不同地区城市化过程中的具体情况制定节能减排政策,做到有的放矢。目前在全国范围内,城市化进程中,城市人口规模的扩大有利于降低人口边际能源消耗,但在扩大城市人口规模的同时应当提高城市人口素质和公众的环保意识。③在我国城市经济发展仍以第二产业为主导,相比于其他产业,第二产业能源消耗较高,特别是西部地区第二产业在今后城市化进程中占比会更高，因此各地区仍需要调整产业结构、加快制造业升级。