基于IBA-ELM的发动机燃油系统故障诊断研究
2018-11-30靖婉婷王海瑞林雅慧
靖婉婷 王海瑞 林雅慧
(昆明理工大学信息工程与自动化学院 云南 昆明 650500)
0 引 言
发动机的燃油系统长时间在高温高压的恶劣环境下工作,为整个机械设备提供动力。据权威机构数据统计,在柴油机的各种故障中,燃油系统故障占总体比重高达27%。由此可见,一旦燃油系统发生故障,将会造成整个机械停止工作,带来的经济和其他方面的损失较为严重。
本文提出一种基于改进的蝙蝠算法,优化极限学习机的故障诊断模型来对发动机的燃油系统进行故障诊断,利用传感器实时采集燃油系统的振动信号。首先本文采用小波分解来对采集到的信号进行处理,从而提取其特征向量。然后使用蝙蝠算法来优化极限学习机的相关参数,搭建优化好的极限学习机的网络结构。最后将提取到的特征向量输入到优化好的极限学习机中进行训练和测试,得到最终的故障诊断结果。本文设置对比实验来验证该模型的合理性和优越性,实验结果表明本文所提方法具有良好的性能。
1 蝙蝠算法
蝙蝠算法是由剑桥大学Xin-she Yang教授在2010年提出的一种基于蝙蝠回声定位的新型群体智能优化算法[1]。
1.1 标准蝙蝠算法
蝙蝠算法的思想是基于蝙蝠回声定位的新型群体智能优化算法,其基本流程概括如下:
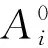
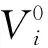

fi=fmin+(fmax-fmin)·β
(1)
(2)
(3)
式中:β是随机变量,且β~U[0,1];X*代表目前搜索范围内的全局最优位置;t表示目前的迭代次数。
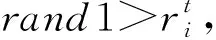
(4)
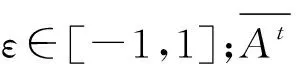
步骤5计算种群内所有蝙蝠个体的新解位置的适应度值。
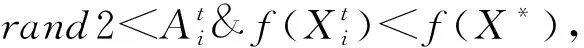
(5)
(6)
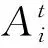
步骤7更新找到的全局最优解,判断是否达到寻优终止条件;若满足则输出X*,若不满足则跳转至步骤3。
1.2 改进的蝙蝠算法
由于蝙蝠算法需要初始化确定的参数个数较多,直到现在还没有人对这一领域做深入的研究。为了提高蝙蝠算法的寻优能力,本文对其做如下改进,根据式(2)和式(3)可得:
(7)
(8)
由此可以更新位置公式为:
(9)
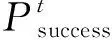
(10)
(11)
(12)
2 极限学习机及其改进算法
2.1 极限学习机
极限学习机ELM是南洋理工大学的黄广斌教授在2004年提出的一种简单易用的单隐层前馈神经网络(SLFN)学习算法[5-6]。在极限学习机算法中需要人为设置的只有隐含层的节点个数这一个参数,而其输入权值和隐含层的阈值是随机生成的[10-11],因此该算法的学习时间极短。 ELM的整体结构如图1所示。
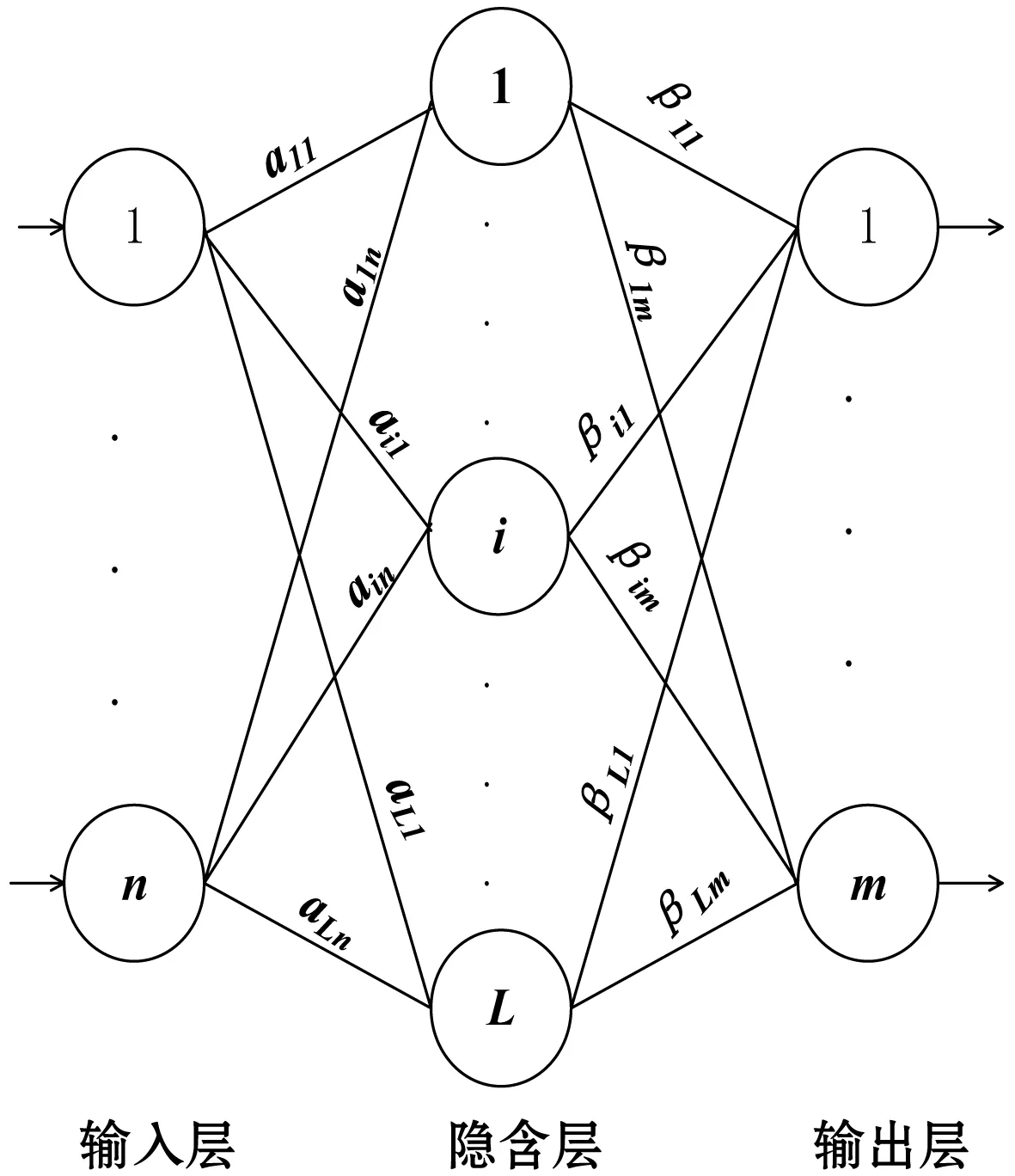
图1 ELM的网络结构
根据单隐层前馈神经网络的相关知识,对于N个不同的训练样本集{(Xi,Ti)|i=1,2,…,N},其中Xi=[xi1,xi2,…,xin]T∈Rn为输入的训练样本,Ti=[ti1,ti2,…,tim]T∈Rm为期望的目标函数,则含有隐含层节点数为L的单隐层前馈神经网络的数学模型为:
(13)
式中:g(x)为隐含层的激活函数;ai=[ai1,ai2,ain]T表示输入权值向量;bi表示隐含层的偏置;βi=[βi1,βi2,…,βim]T表示输出权值向量。
将式(13)写成矩阵的形式为:
Hβ=T
(14)
式中:输出矩阵
H(a1,a2,…,aL,b1,b2,…,bL,x1,x2,…,xN)=
随机产生输入权重ai阈值bi后,就可以根据式(14)计算得到ELM网络的各个参数。由式(14)转化即可得:
β=H+T
(15)
式中:H+表示隐含层输出矩阵H的Moore-Penrose广义逆矩阵[12-14]。求出输出权重,再加上随机产生的其他权重和阈值参数,整个ELM网络就确定了。
2.2 基于改进的蝙蝠算法优化极限学习机
鉴于极限学习机和改进的蝙蝠算法各自的优缺点,本文将两种算法结合在一起,从而提出一种基于改进蝙蝠算法优化极限学习机(IBA-ELM)的发动机燃油系统故障诊断模型。该模型的主要思想是改进极限学习机的输入权值和阈值随机生成。本文利用改进的蝙蝠算法来优化权值和阈值的选择过程,从而选出一组最优的参数组合来提高极限学习机的工作性能。基于改进蝙幅算法优化极限学习机的流程如图2所示。
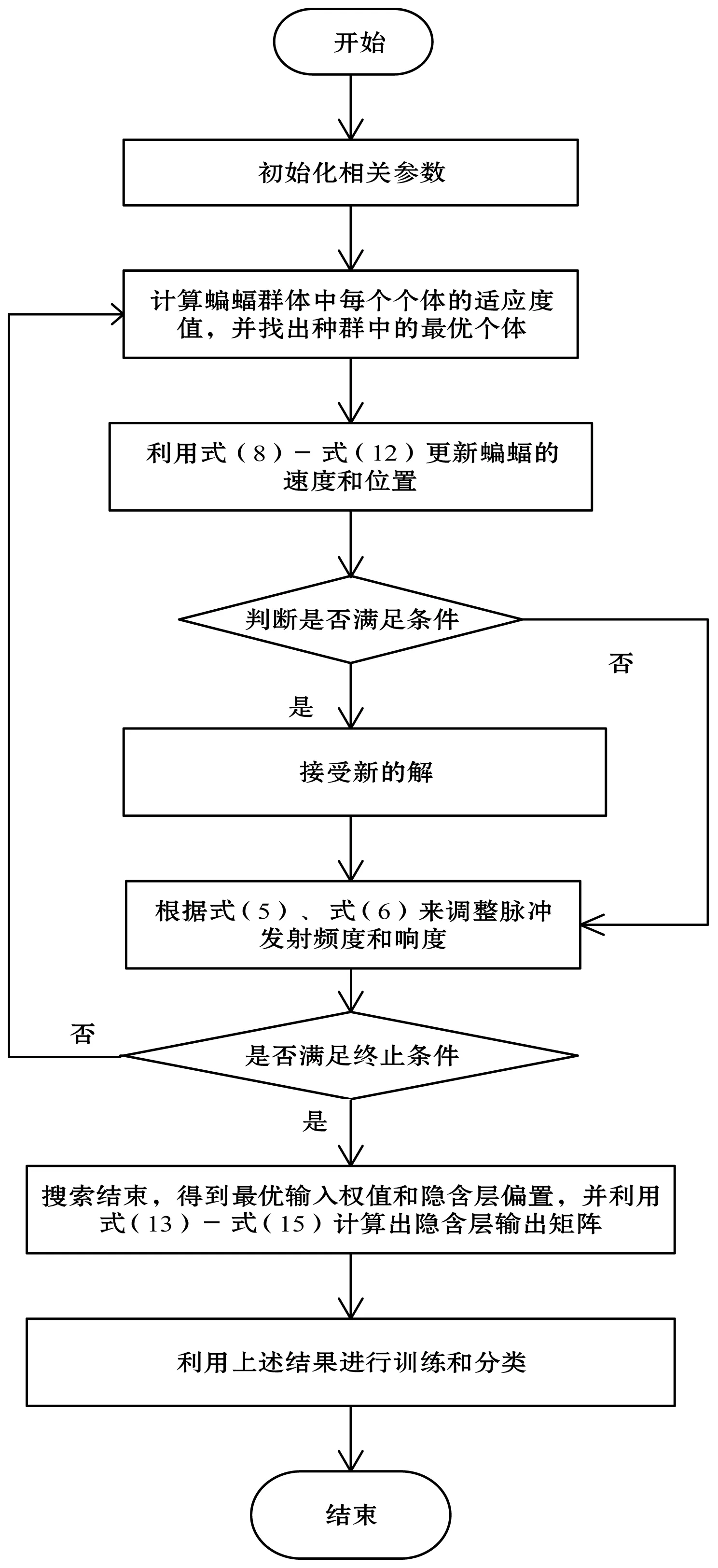
图2 基于改进蝙幅算法优化极限学习机流程图
3 实验及结果分析
3.1 样本选择及特征提取
实验以某型号柴油机燃油系统为研究对象,采用传感器来进行故障信号的采集,以MATLAB 2010b为实验平台。通过小波3层分解对原始信号进行分解重构,最终获得8个特征参数,将其组成特征向量P=[P1,P2,P3,P4,P5,P6,P7,P8]作为诊断输入。样本故障类型选取柴油机燃油系统的6个常见故障,故障输出以二进制的形式表示,因此故障分类及对应表示如表1所示。
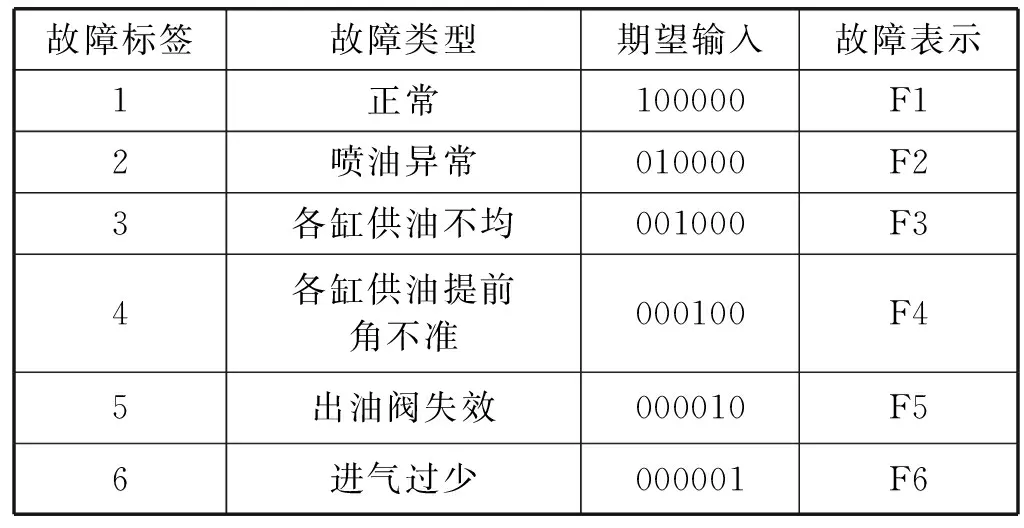
表1 柴油机燃油系统的故障分类及对应表示
实验选取样本总数为900组,则6种故障每种故障分别选取150组,其中120组作为训练输入样本,剩余30组录入为预测样本集。
3.2 实验比较分析
3.2.1 优化算法性能比较
本实验设置了如下4种实验模型。初始化4种算法参数:4种算法的规模数量和最大迭代次数均取100;粒子群算法的惯性权重γ、加速常数c1和c2分别取0.6、2、2;遗传算法的参数因子代沟、交叉概率和变异概率分别取0.95、0.7、0.01;BA算法其搜索脉冲频率设置在[0,10]范围内,IBA算法设置在[0.5,10.5]范围内,脉冲响度衰减系数和脉冲频度增加系数γ分别取0.95、0.9。最终,对比实验可得适应度曲线对比如图3所示。
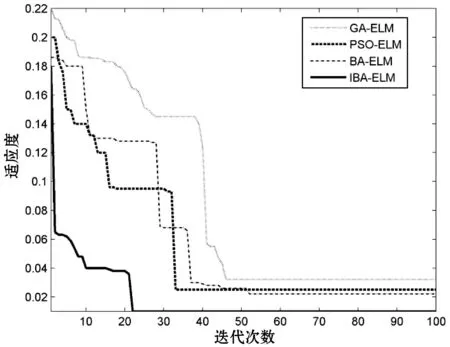
图3 4种优化算法优化ELM适应度曲线
由图3的适应度迭代曲线可得到:4种算法在优化ELM过程中的适应度都随着迭代代数的增多呈现收敛状态,因而都能够得到最优权值和阈值;GA算法在46代左右趋于收敛,但实验发现GA寻优进化过程中后期搜索效率较低;PSO算法在33代左右趋于收敛,但寻优结果远不如IBA算法;BA算法虽然最优值优于GA和PSO,但是寻优最终结果不如IBA,且该算法优化ELM在52代左右才收敛得到最终最优解,迭代次数不理想;IBA在BA的基础上改进了初始数据,并引进惯性权重系数、重置最终判定条件,进而约减适应度较弱个体,最终达到优化BA的效果,解决了BA迭代次数多、收敛速度慢的缺点。同时该方法在22代左右适应度函数值趋于收敛取得最优,收敛速度快,且寻优所得结果远比其他三种优化算法所得结果优质。因此,使用IBA算法优化极限学习机具有较为显著的效果。
3.2.2 分类模型比较
为了验证本文提出的IBA-ELM方法的性能在燃油系统故障诊断更胜一筹。本实验将IBA-ELM诊断方法与支持向量机(SVM)、传统极限学习(ELM)、蝙蝠算法优化的极限学习机(BA-ELM)进行比较。4种模型分别独立运行10次,得到4种分类结果精确度的比较如图4所示。训练时间和测试时间的比较如图5所示。
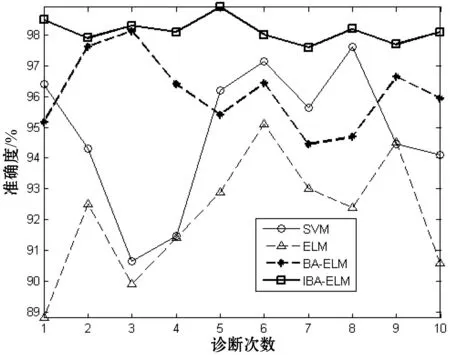
图4 4种模型分类精确度的比较
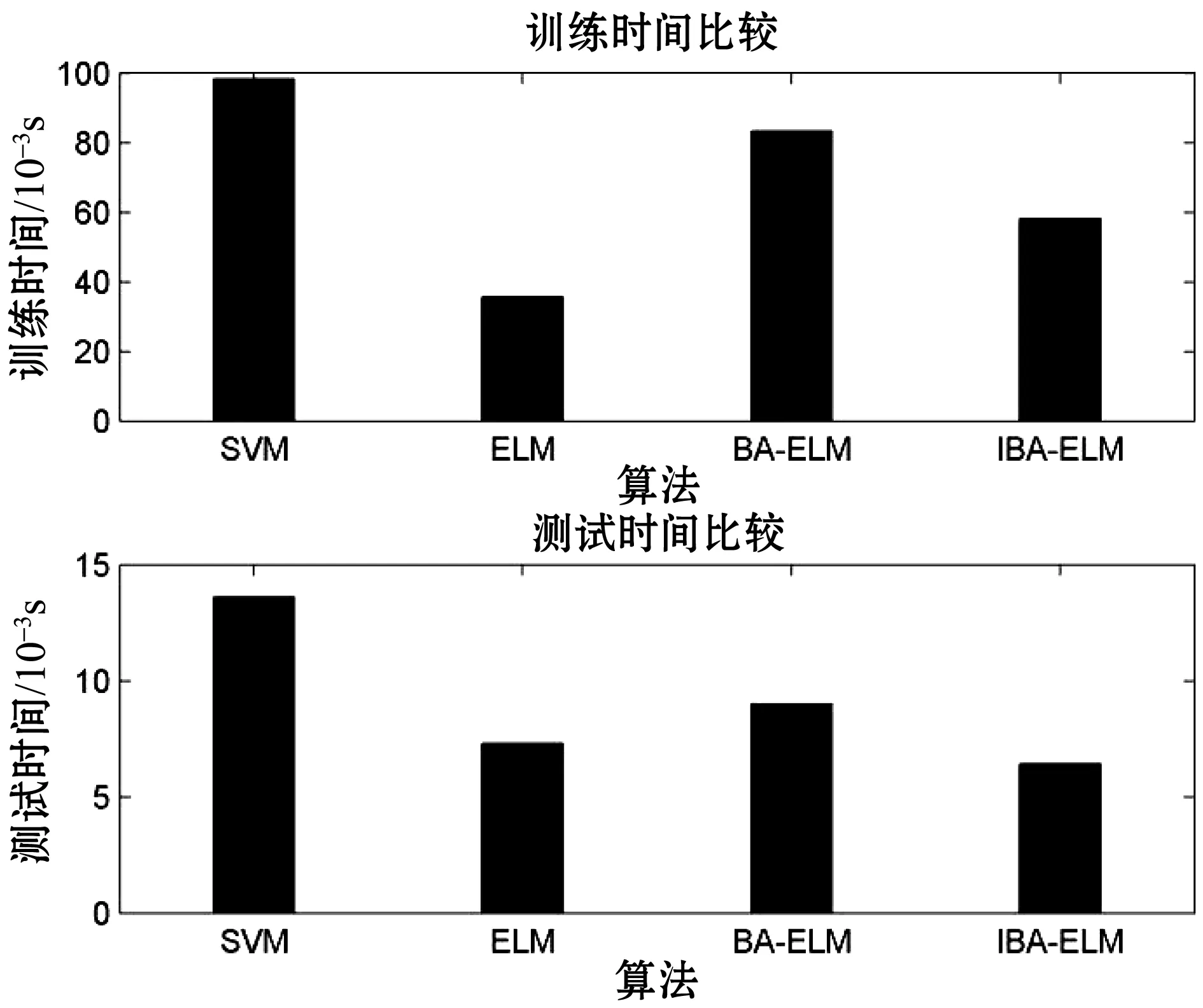
图5 4种模型的训练时间和测试时间
由图4和图5,可以得出表2的性能分析:SVM方法分类准确率高,但训练模型以及测试样本速度慢。由于在燃油系统诊断过程中,准确率的高低和速度的快慢决定了诊断的性能,两者缺一不可,所以本文考虑选用极限学习机。极限学习机训练测试时间非常快,但明显准确率不如支持向量机。因而选用蝙蝠算法优化极限学习机,得到准确率明显高于支持向量机和传统极限学习机,但速度还是不如传统极限学习机。最后采用IBA优化ELM,速度和准确度相对于BA优化ELM大大地提升,经4种方法比较,其速度仅次于传统ELM。实验表明了IBA-ELM在燃油系统故障诊断中不仅分类速度快,而且能有效地提高诊断的准确率。
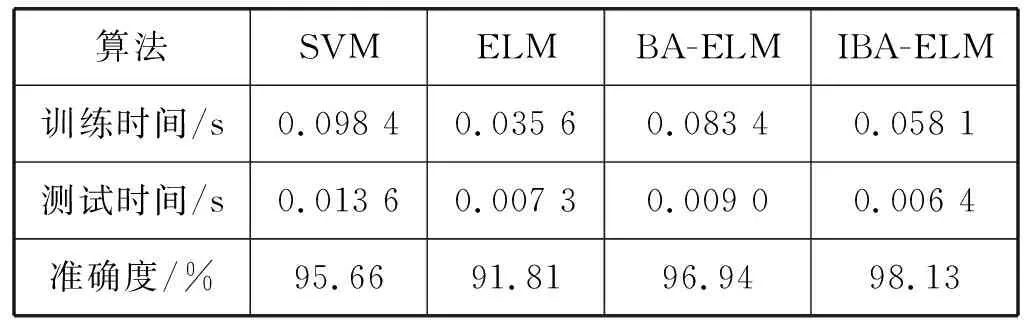
表2 4种模型性能比较
3.2.3 实际与预测值比较
为了测试IBA-ELM燃油机系统诊断模型的分类准确率,实验将用于训练模型后剩余的180组测试样本集输入已形成的IBA-ELM模型进行预测,并将预测结果与实际输出真值作比较。得到IBA-ELM模型预测结果与实际输出真值比较如表3所示。IBA-ELM模型测试集分类图,如图6所示。
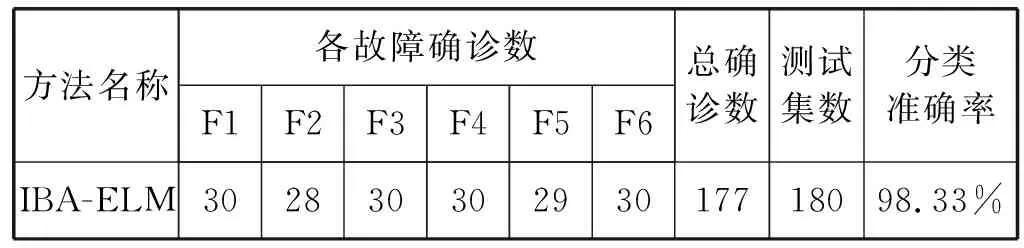
表3 IBA-ELM模型预测结果与实际输出真值比较
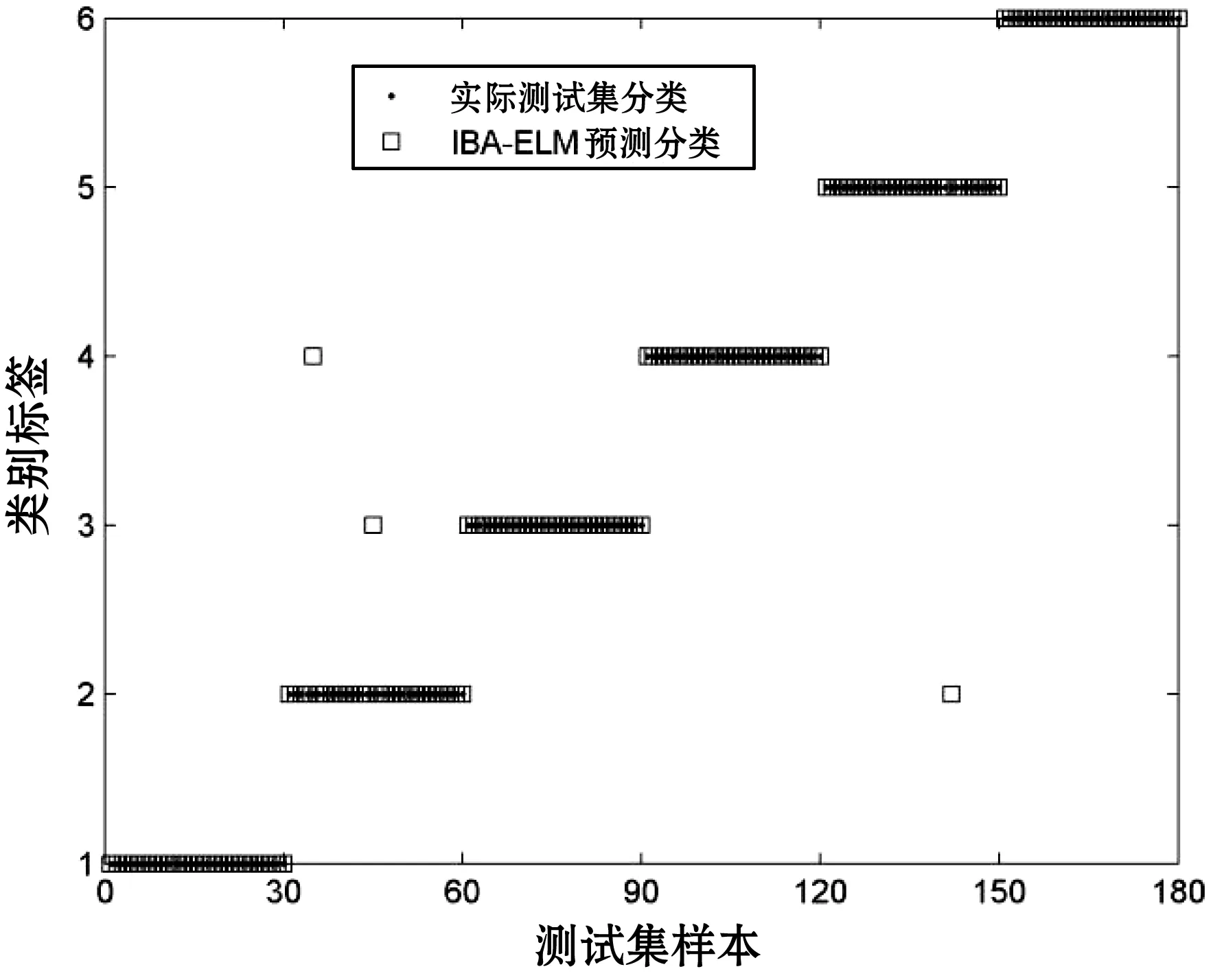
图6 IBA-ELM模型测试集分类图
由表3、图6可得,对180组预测样本集进行预测输出时,诊断正确组数为177组,说明只误判了3组,预测精度高达98.33%。综上所述:IBA-ELM模型具有较高的预测精度,并且能够准确地预测出燃油机故障系统的故障类型。
4 结 语
本文提出一种基于改进的蝙蝠算法优化极限学习机的发动机燃油系统故障诊断模型。通过设置适应度对比、诊断准确率比较和训练时间与测试时间的比较等一系列对比实验,证明了该模型的有效性以及稳定性。并且该模型在发动机燃油系统的故障诊断中具有很好实用效果。
