基于时间序列嵌入的电力负荷预测方法

田英杰 苏 运 郭乃网 姚 博 庞 悦 周向东

1(国网上海市电力公司电力科学研究院 上海 200437)2(复旦大学计算机科学技术学院 上海 200433))

0 引 言

为了提高发电和配电效率，尽量减少能源浪费，确保可持续发展，我们的电网正向智能电网转变[1-2]。智能电网能够根据需求的变化，动态调整电力生产和分配的方案，为能源管理提供前所未有的灵活性[3-4]；为了实现这一转变，预测未来需求的能力非常重要[5]。智能的能源管理方案不仅能在电网的聚合层级上，根据需求的变化做出动态调整；在个体层级上，也应具有动态调整的能力[6]。智能电表的出现使得个体层级电力负荷的采集成为可能，进而针对个体层级的负荷需求预测和方案动态调整也成为可能[3]。

电力负荷预测的难点在于个体层级的负荷具有高度的波动性和不确定性[7, 24-26]。通过聚合(抵消波动性和不确定性)能够避开这一难点；针对聚合层级负荷预测的问题，已有许多工作提出了有效的预测方法[8-23]。然而，由于存在高度的波动性和不确定性[24-26]，在个体层级上的负荷预测仍具有挑战性[7]；相关的工作数量有限，且预测的精度不高[6-8, 24-32]。在个体层级上，一条电力时间序列(如图1(a)所示)可以分解成三个部分：(1) Regular Pattern(如图1(b)所示)；(2) Uncertainty(如图1(c)所示)；(3) Noise(或Volatility，如图1(d)所示)。其中：Regular Pattern是电力负荷固有的周期性部分(以日、周、年等为周期)；Uncertainty是受天气、偶然事件等外部因素影响的非周期性部分；Noise(或Volatility)是不能从物理上解释的剩余部分[8-9]。

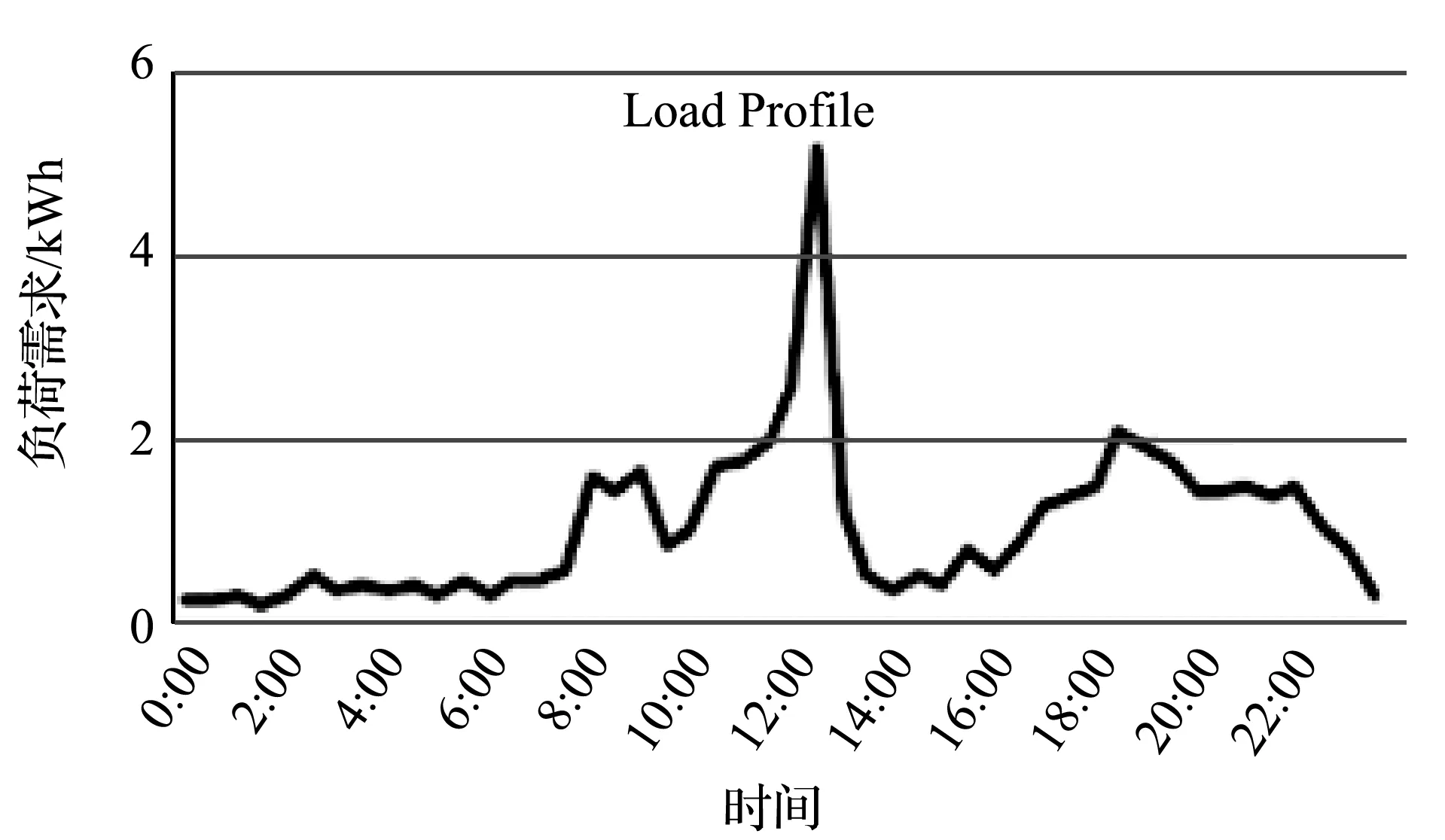
(a)

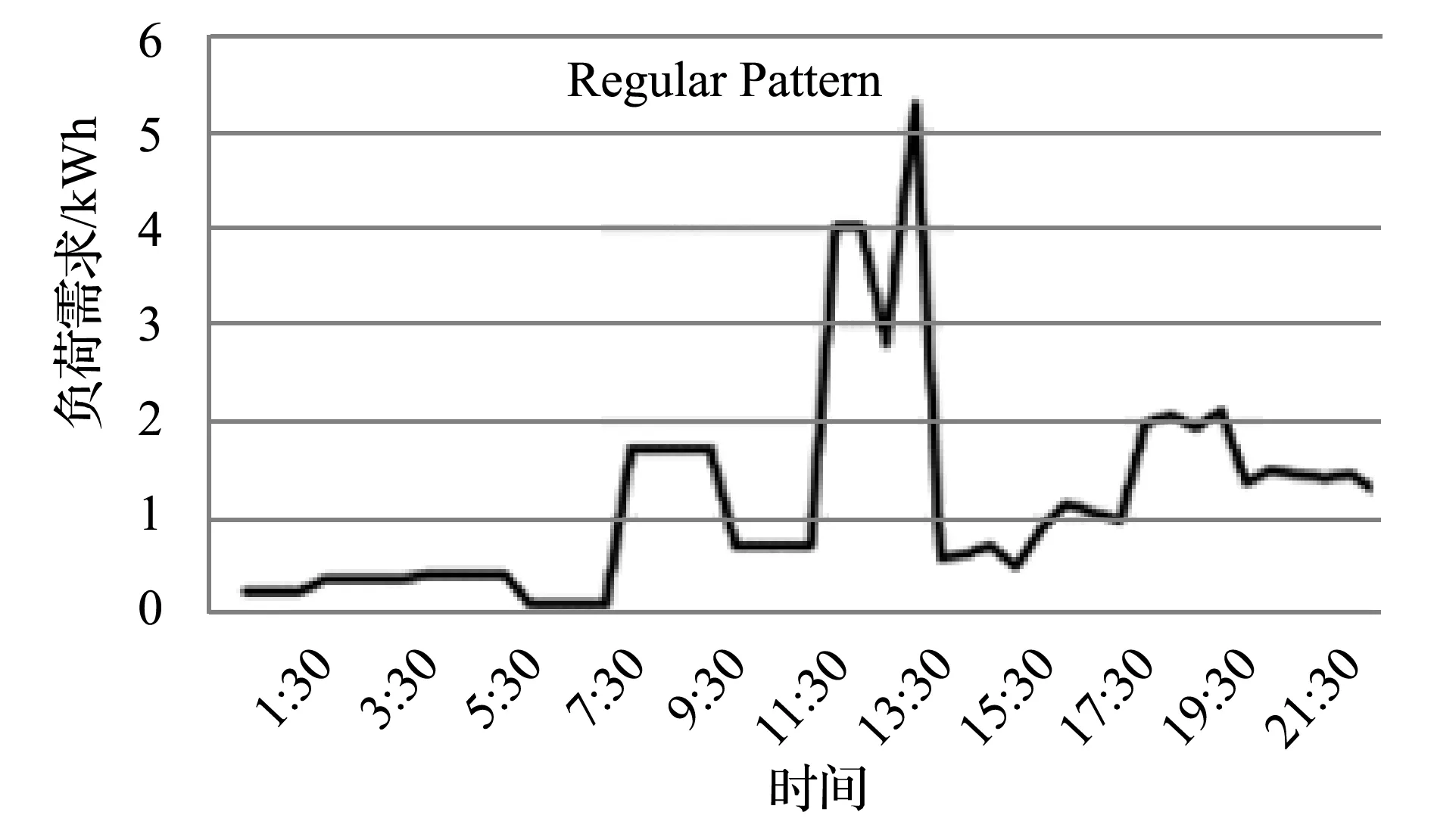
(b)

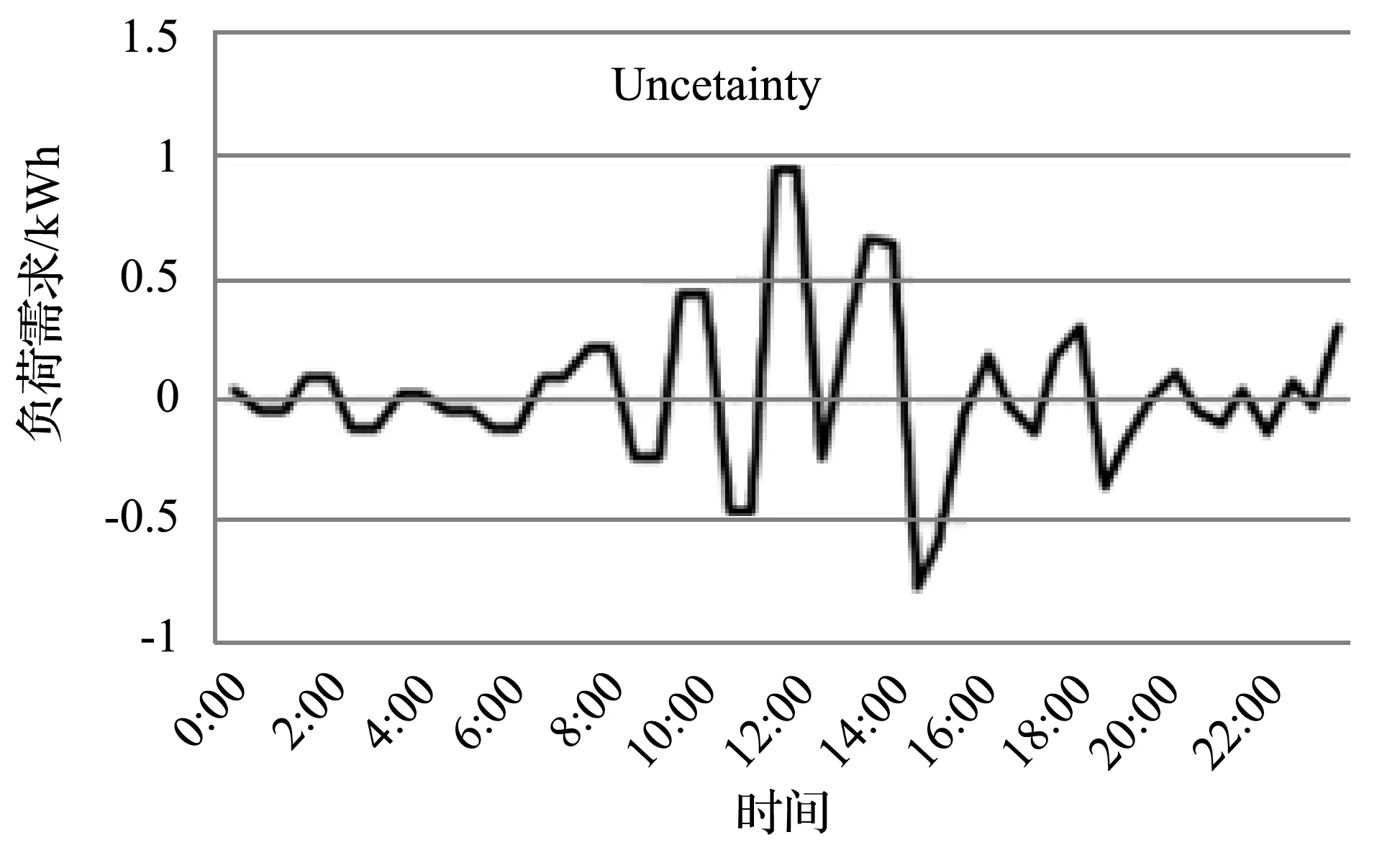
(c)

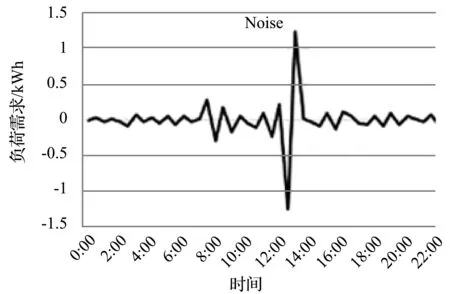
(d)图1 电力时间序列的分解

事实上，周期性部分Regular Pattern是容易预测的。但非周期性部分Uncertainty的预测是困难的，原因在于：(1) 外因数据的采集是困难的，甚至是不可行的；(2) 非周期性部分固有的随机性是不可预测的。此外，噪声Noise(或波动性Volatility)也是不可预测的。在个体层级上，非周期性部分Uncertainty和噪声Noise具有相对高的占比，使得电力负荷的预测具有挑战性[7, 24-26]；现有的工作[6-8, 24-32]不能有效解决高度的不确定性和波动性带来的困难，预测的精度不高。

个股股价也具有高度的不确定性和波动性，文献[33]运用自动编码器AE(Autoencoder)生成股价时间序列的嵌入，使用嵌入而非原始序列预测未来的股价。在沪深两市部分股票上进行的对比实验表明，相比于传统方法，AE生成的嵌入能够提取股价时间序列深度的特征，过滤其噪声，进而提升预测的精度。然而，由于股价时间序列没有明显的周期性，直接采用这一方法预测个体层级的电力负荷，生成的嵌入捕捉负荷周期特性的能力有限，预测精度的提升不大。

针对现有方法存在的不足，提出一种基于时间序列嵌入的电力负荷预测方法。根据电力负荷固有的周期特性(以日、周、年等为周期)，设计周期自动编码器PAE，按周期将电力时间序列嵌入一个统一的向量空间。在嵌入空间中，可以采用多种深度神经网络模型，来预测未来的电力负荷。实验结果表明，PAE生成的嵌入能够捕捉电力负荷固有的周期特性，过滤其不确定性和波动性。因此，相比于传统方法，本文提出的预测方法具有更高的预测精度。

1 相关工作

针对聚合层级负荷预测的问题，已有许多工作提出了相对准确的预测方法[8-23]。文献[10]提出在负荷预测之前，使用聚类识别具有类似负荷消费模式的消费者，进而提高系统层级日内负荷预测的精度。文献[11]认为天气是电力需求的主要驱动因素，气象站的选择对电力负荷的预测起重要作用。因此，提出一个气象站选择框架，以确定某个感兴趣的地区使用哪个气象站。实验结果表明，这一框架可以提高负荷预测的精度。文献[13]也认为温度在驱动电力需求方面起着关键的作用；他们采用心理学术语“近因效应”来表示电力需求受前几小时气温影响的事实，据此，建立负荷预测模型。文献[14]等提出一种基于层次结构的预测方法，捕捉不同层次节点的负荷特性，利用父节点与其子节点之间的模式相似性，检测异常，提高预测的精度。文献[15]提出一种基于贡献因子的方法来预测低压变电站的日常峰值负荷；贡献因子由聚类加权约束回归确定，描述了不同消费者对变电站峰值的贡献程度。文献[17]提出一个共享相似模型结构但基于不同变量选择过程的模型簇，在2014全球能源预测大赛上，这一模型簇的预测精度显著高于基准方法。

针对个体层级负荷预测的问题，相关的工作数量有限，且预测的精度不高[6-8, 24-32]。文献[6]等提出一种基于深度神经网络的电力负荷预测方法，针对标准长短期记忆网络LSTM存在的不足，设计基于LSTM的S2S结构，有效提升预测的精度。文献[7]提出一种池化负荷曲线的深度学习方法，来预测个体层级的电力负荷。这一方法能够缓解深度学习过度拟合的问题，进而获得更高的预测精度。文献[24]提出一种基于马尔可夫链的人类行为实践理论抽样技术，能够降低预测对历史数据的需求。历史数据不够充分的情况下，这一方法能够显著提升预测精度。文献[25]针对在低压网络中注入能量会导致高电压限制的问题，提出一种短期功耗时间序列预测的方法。实验结果表明，这一方法能够提升短期预测的精度，帮助平衡低压网络的供需。文献[32]提出一种基于情境信息和日程安排模式分析的个体短期负荷预测方法，分析日常电力时间序列，得到不同的日常行为模式类型，并收集各种来源的情景特征，以建立负荷预测模型。

2 电力负荷预测

针对个体层级负荷预测的问题，如图2所示，本文提出的方法首先运用周期自动编码器PAE，按周期将这一层级的电力时间序列嵌入向量空间。随后将生成的嵌入(而非原始序列)输入预测器，预测未来的电力负荷。事实上，可以选择多种深度神经网络模型作为预测器，本文以多层感知器MLP为例，具体介绍提出的负荷预测方法。

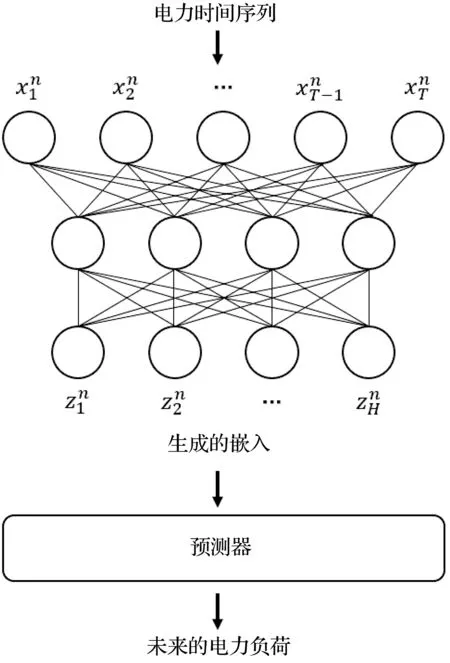
图2 基于时间序列嵌入的电力负荷预测方法

2.1 个体层级的负荷预测

给定N个个体的历史电力时间序列：

X=(x1,x2,…,xN)′=(x1,x2,…,xT)∈RN×T

(1)

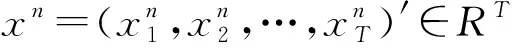
本文研究的问题是：给定上述历史电力时间序列X，如何准确预测未来一段时间内，这N个个体的电力负荷：

Y=(y1,y2,…,yN)′=(y1,y2,…,yQ)∈RN×Q

(2)

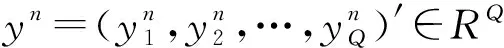
事实上，这一问题的本质是：针对某个个体n，如何学习一个从xn到yn的非线性映射f:RT→RH，使得预测精度的评价指标(例如，均方根误差RMSE、平均绝对百分比误差MAPE等)尽可能地好；针对N个个体，如何学习N个这样的映射，使得总体的预测精度的评价指标尽可能好。文献[7]发现：如果上述非线性映射f:RT→RH用深度神经网络实现；这N个个体共享同一个映射(即采用同一种预测模型且个体间共享模型参数) 能够缓解深度学习过度拟合的问题，进而获得更高的预测精度。因此，在本文提出的方法中，这N个个体也共享同一个映射。

2.2 基于周期自动编码器的负荷预测

个体层级负荷预测的难点在于这一层级的负荷具有高度的波动性和不确定性[7, 24-26]。现有的工作[6-8, 24-32]不能克服这一难点，预测的精度不高。文献[33]等针对个股股价高度的波动性和不确定性，先运用自动编码器AE，去生成历史股价时间序列的嵌入；再使用生成的嵌入(而非原始的历史序列)去预测未来的股价。生成的嵌入不仅能提取历史股价时间序列深度的特征，还能过滤其噪声。因此，与直接使用原始的历史序列做预测的方法相比，这一方法具有更高的预测精度。然而，由于股价时间序列没有明显的周期性，直接采用这一方法去预测个体层级的电力负荷，生成的嵌入捕捉负荷周期特性的能力有限，预测精度的提升不大。

针对现有方法存在的不足，根据电力负荷固有的周期特性，提出周期自动编码器PAE，其结构如图3所示。

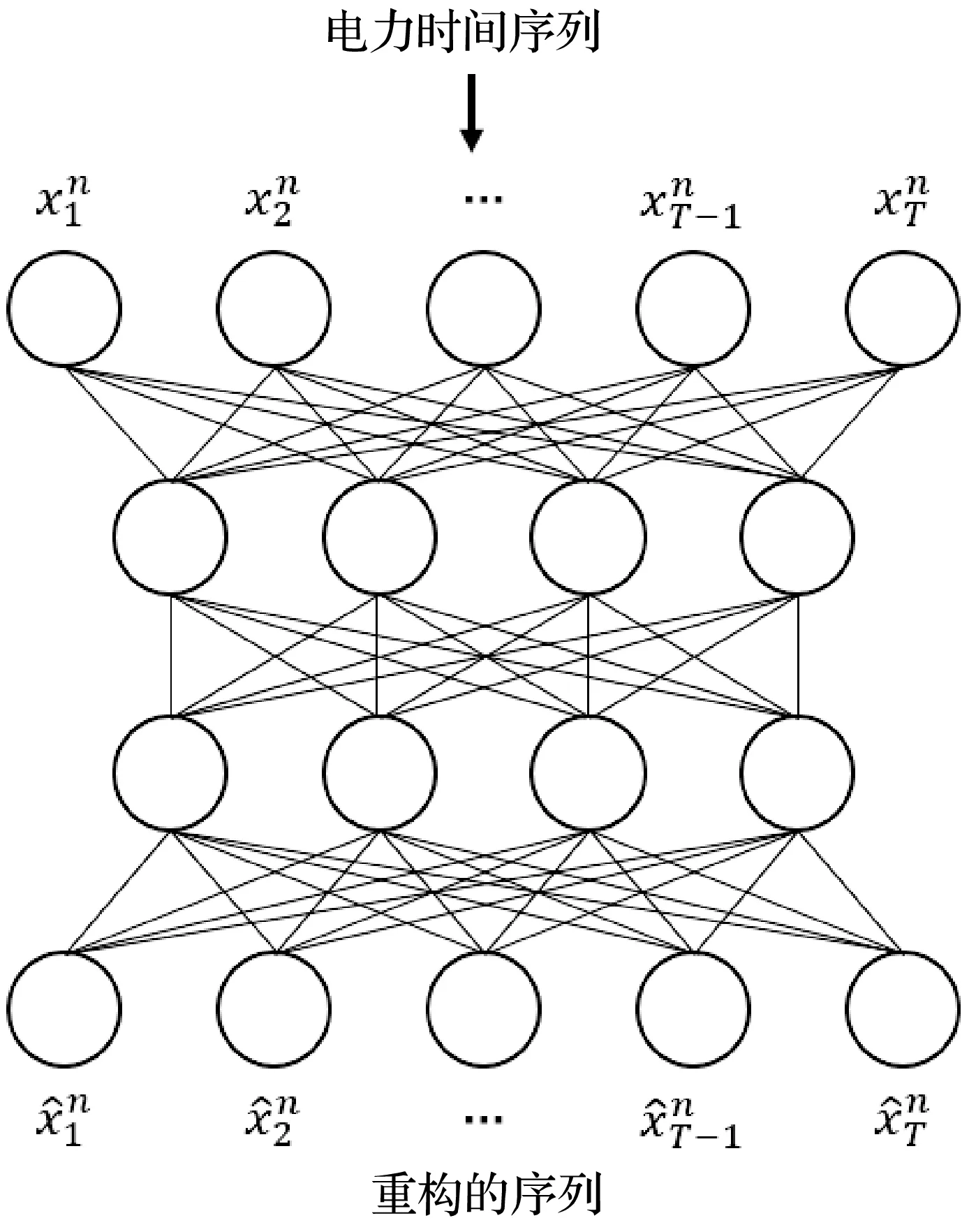
图3 周期自动编码器

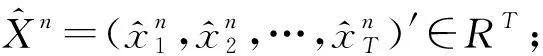
(3)

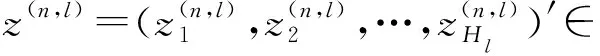
根据电力负荷固有的周期特性(设其周期为T0)，PAE按周期(历史窗口的长度T取kT0,k∈N+)将上述N个个体的历史电力时间序列X嵌入向量空间RH。为了缓解过拟合，这N个个体共享同一个PAE网络(即共享同一个映射)；训练模型的损失函数是均方根误差RMSE：

(4)

(5)

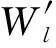
(6)

实验结果表明，PAE生成的嵌入不仅能捕捉电力负荷固有的周期特性，还能过滤其不确定性和波动性。因此，与传统方法相比，本文提出的方法具有更高的预测精度。

3 实 验

(1) 实验数据 实验使用的数据集来自英国能源需求研究项目EDRP(Energy Demand Research Project)[34]。这一项目旨在帮助英国政府更好地了解国内家庭用户的能源消费模式，并据此做出相应的能源政策调整。我们使用了其中152个家庭用户110天的电力时间序列(从2009年5月9日至2009年8月24日；每半小时采集一次电力负荷，每日48个点，110天共计5 280个点)。基于时间序列嵌入的电力负荷预测。

(2) 基于嵌入的负荷预测 为了表明使用嵌入(而非原始序列)去预测未来的电力负荷，能够提升预测的精度，我们在EDRP数据集上进行了对比实验：除了预测器的输入不同外(分别为嵌入和原始序列)，其他可能影响预测精度的因素均保持一致(例如，预测器均采用多层感知器MLP，目标函数均为RMSE，优化算法均为Adam等)。实验中，针对每个家庭用户，首先使用其第1天的48个点去预测第2天的48个点；随后使用其第1天和第2天的96个点去预测第3天的48个点，实验的结果如表1所示。

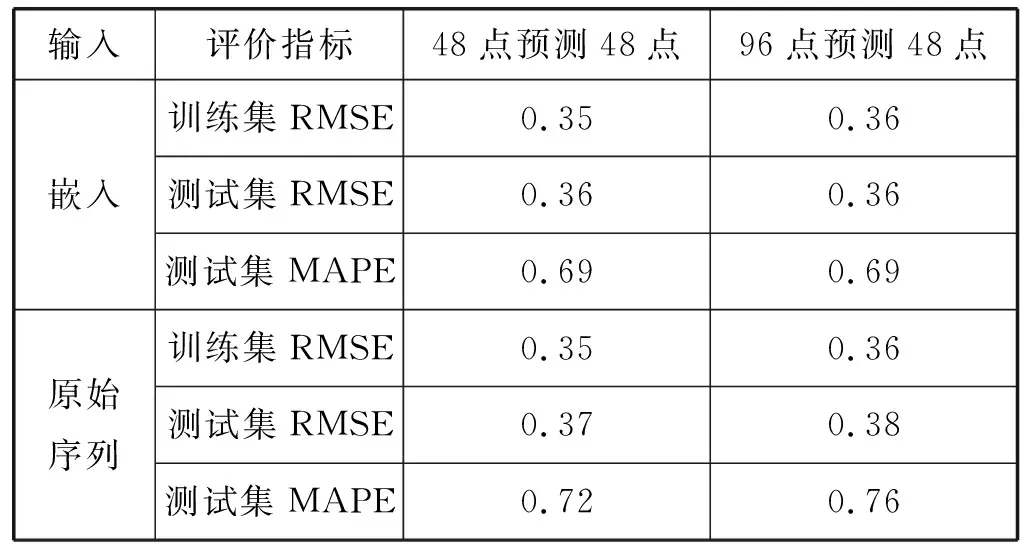
表1 嵌入与非嵌入的预测精度对比

此外，图4展示了在训练预测器的过程中，随着训练轮数的增加，测试集均方根误差RMSE的变化曲线；其横轴为训练的轮数，其纵轴为RMSE的值。从表1和图4中可以看出，PAE生成的嵌入能过滤电力负荷高度的不确定性和波动性。因此，使用PAE生成的嵌入(而非原始序列)去预测未来的电力负荷，不仅能获得更高的预测精度，还能使训练过程更加稳定且不易过拟合(预测模型不易学习到历史序列中，随机波动的噪声的特征)。

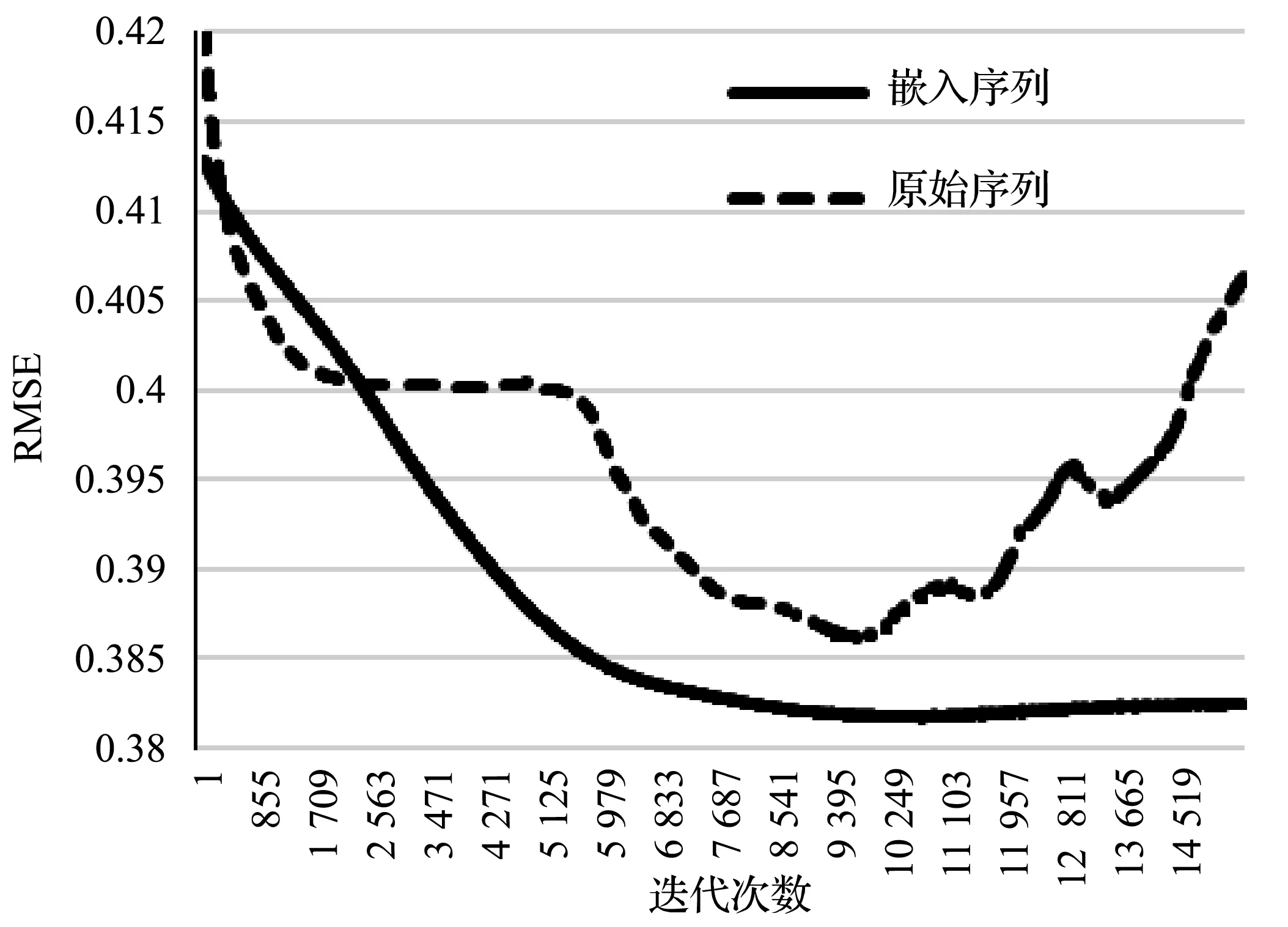
(a) 48点预测48点

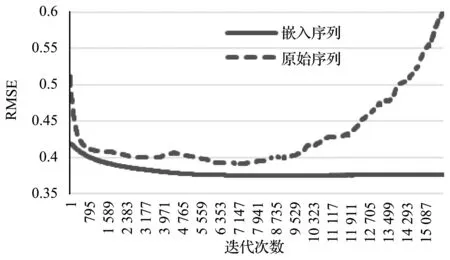
(b) 96点预测48点图4 测试集的RMSE的变化曲线

(3) 基于周期特性的嵌入生成预测 为了表明周期自动编码器PAE生成的嵌入能捕捉电力负荷固有的周期特性，进而能提高预测的精度，我们在EDRP数据集上进行了另一组对比实验：PAE按周期将历史电力时间序列嵌入向量空间，传统的嵌入方法不按周期生成嵌入；其余影响因素均保持一致。类似地，针对每个家庭用户，首先，PAE使用其第1天的48个点去预测第2天的48个点(传统的嵌入方法使用前50个点去预测后48个点)。随后，PAE使用该用户第1天和第2天的96个点去预测第3天的48个点(传统的嵌入方法使用前100个点去预测后48个点)，实验的结果如表2所示。可以看出传统的嵌入方法没有捕捉到对于电力负荷预测十分重要的周期特性，尽管增加了历史用电的信息，预测的精度反而不高。与之相比，PAE生成的嵌入能捕捉电力负荷固有的周期特性，进而能获得更高的精度。

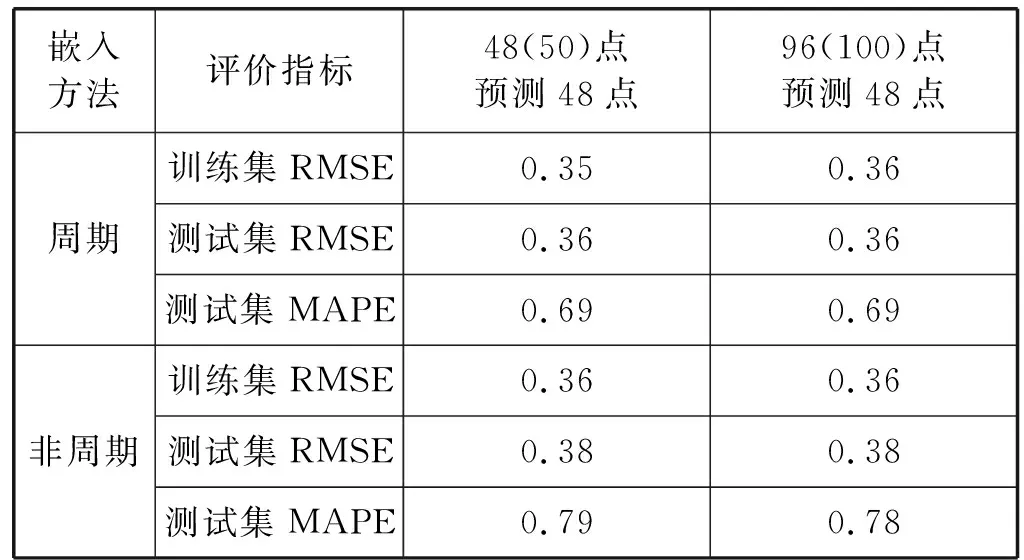
表2 周期与非周期的预测精度对比

4 结 语

针对个体层级负荷预测的问题，本文总结了现有方法存在的不足，提出一种基于时间序列嵌入的电力负荷预测方法。根据电力负荷固有的周期特性(以日、周、年等为周期)，设计周期自动编码器PAE，按周期将电力时间序列嵌入向量空间。在嵌入空间中，可以采用多种深度神经网络模型，来预测个体层级的电力负荷。实验结果表明，PAE生成的嵌入能够捕捉电力负荷固有的周期特性，过滤其不确定性和波动性。因此，相比于传统方法，本文提出的预测方法具有更高的预测精度。