社会消费品零售总额的预测

【摘要】社会消费品零售总额是研究人民生活、社会消费品购买力、货币流通等问题的重要指标，社会消费品零售总额能够反映消费的主要情况，使用不同年份的数据能够更好的发现消费的成长性和趋势变化，帮助我国制定宏观经济政策提供有力帮助。本文基于2006年1月至2017年11月的我国社会消费品零售总额时间序列数据，构建了ARIMA（0，1，1）×（0，1，2）12模型，并对2017年12月至2018年12月的社会消费品零售总额进行外推预测，以此对我国未来一年的消费水平有一个整体了解，从宏观层面把握我国未来经济运行状况。

【关键词】社会消费品零售总额 季节ARIMA模型 预测

伴随着人们对消费需求的讨论，各个经济学者越来越关注社会消费品零售总额这个指标。社会消费品零售总额是指批发和零售业、餐饮业、新闻出版业、邮政业和其他服务业等售予城乡居民用于生活消费的商品和社会集团用于公共消费的商品之总量。这个指标能够反映消费的主要情况，是研究人民生活、社会消费品购买力、货币流通等问题的重要指标。同时，各年度的社会消费品零售总额不仅可以反映一个社会当期的消费水平，也能反映出消费的成长潜力和趋势，进而反映出对经济的拉动程度，因而也是制定宏观经济政策的一个重要参考指标。因此，合理预测未来的社会消费品零售总额，不但可以了解我国消费需求情况，对我国未来经济运行状况做到“心中有数”，同时也可以为我国制定宏观经济政策提供重要的参考依据。

本文将应用我国2006年1月至2017年11月的消费品零售总额的月份数据，通过分析数据特点，建立合适的季节ARIMA模型，在此基础上对我国社会消费品零售总额进行预测，并对预测的结果进行评价。

一、文献综述

一部分学者研究各种因素对社会消费品零售总额的影响程度。如：邹洋（2017）从国内增值税和商品房屋销售面积两个方面对社会消费品零售总额分析，并解释了其经济意义。王文倩、王红艳、李梅芳（2016）发现国内社会消费品零售总额是一种整体周期性波动上升；构建的模型为预测2016年我国社会消费品零售总额提供了较为有效的技术支持。得出的结论是：要想促进社会消费健康的发展，需要健全社会保障机制，提高人民消费水平；同时加强市场监管力度，规范整个市场经济秩序；扩大社会投资规模，提升社会消费需求。刘亚男（2007）构建了多元线性回归模型研究社会消费零售总额，得出的结论为影响主要因素是由农村居民家庭人均纯收入决定的，可以通过大幅增加农民纯收入来促进整个社会的消费水平。法丽娜（2010）从模型假定、参数估计、其他检验方式得出结论：只有收入和消费能保持很好的线性相关性，因此在当前经济情况下，如果要刺激消费，最关键的在于提高居民的人均可支配收入。于书娇（2016）研究了人民币汇率的变动对我国社会消费品零售总额的影响情况，数据基础为2005年7月到2014年12月的社会消费品零售总额及汇率，进而通过分析得出两者相关关系。

还有一部分学者研究社会消费品零售总额的趋势和预测未来的方向。如：王哲、颜卫忠（2017）对国内社会消费品零售总额的影响因素进行分析，再通过建立线性回归方程对其进行预测。并对比ARIMA预测方法，得到时间序列模型预测结果更准确，从而为政府决策提供科学依据。孙艳、彭阳阳（2016）利用1984到2014年国内社会消费品零售额的月度数据，并结合霍尔特-温特斯指数平滑法的加法、乘法模型，因考虑到时间序列可能同时受到多重季节周期因素的影响，故采用霍尔特-温特斯乘法模型进行拟合分析。结果发现考虑双重季节周期的乘法模型预测精准度更高，且误差较低，更符合现实生活中的情况。巨薪渝（2016）研究以2004年1月至2015年5月我国社会消费品零售总额的月度数据，使用ARIMA模型进行时间序列模型分析，并对我国社会消费品零售总额2015年6月到12月的数据进行了预测。方湖柳（2009）通过实证得到我国社会消费品零售总额总体呈现季节性和持续发展的趋势。根据文章实证分析提出扩大政府财政支出规模、保障币值稳定、降低储蓄等政策建议。全景月（2013）运用季节时间序列模型（SARIMA），对我国2002年-2011年的社会消费品零售总额进行时间序列模型分析。且通过模型对2012年社会消费品零售总额做了预测，通过和2012年的实际数据比价发现，误差较小，SARIMA模型较好地消除了时间序列的季节因素影响和趋势的变动。

二、数据趋势的初步判断

在进行任何数据分析和建模之前，首先要了解数据的特征分布情况，尤其对于时间序列数据，需要判断数据的时间序列的趋势成分。通过社会消费品零售总额的折线图和年度折线图，可以对社会消费品零售总额有一个整体的把握。如图1所示，总体来看，我国社会消费品零售总额有逐年增长的趋势，带有明显的趋势性，因此可以初步判断该序列是非平稳的。同时，我们还发现，社会消费品零售总额呈现上升-回落-上升的周期性，如此动态上升，换言之，数据具有明显的季节性。

■

图1 社会消费品零售总额的时间序列折线图

三、模型的识别

（一）平稳性检验

直观上来看，社会消费品零售总额数据经过一次差分和季节差分后的数据基本平稳。本文采用ADF检验判断时间序列数据的平稳性。

对社会消费品零售总额经一次差分和季节差分后的数据进行ADF检验，检验的结果如表1所示。因此可以确定，对社会消费品零售总额经一次差分和季节差分后得到的序列是平稳的时间序列。

表1 社会消费品零售总额经一次差分和季节差分后的序列的ADF检验的结果

■

（二）滯后阶数的确定

通过数据的平稳化处理后，再对平稳序列构建时间序列模型。因为社会消费品零售总额数据是非平稳的，且带有明显的季节性，因此，可以初步确定应该构建季节ARIMA模型。进一步地，为了确定季节ARIMA模型ARIMA（p，d，q）×（P，D，Q）12中AR和MA部分的滞后阶数（p、q、P、Q），对社会消费品零售总额经一次差分和季节差分后得到的平稳序列，构建样本自相关函数（ACF）图和偏相关函数（PACF）。经一次差分和季节差分后的序列的样本自相关函数是截尾的，基本上只有1阶和24阶滞后相关系数显著不为零，且序列的样本PACF是拖尾的。因此可以初步考虑用乘法季节模型ARIMA（0，1，1）×（0，1，2）12模型拟合样本数据，即使用的模型为：

D12Dyt=（1+qL）（1+QL12+Q2L24）et

其中■为社会消费品零售总额的时间序列，L为滞后算子，{et}为白噪聲序列，q和Q为未知参数。

四、模型的估计与诊断性检验

（一）模型的估计

确定拟合模型之后，下一步便是估计模型参数，得到确定性模型。本文应用极大似然法估计我国社会消费品零售总额的ARIMA（0，1，1）×（0，1，2）12模型，借助R软件，得到的结果如表2所示：

在5%的显著性水平下，从表2可以看到，所有系数的估计值基本上都是显著的，下面进一步对模型进行诊断性检验。

（二）模型的诊断性检验

模型的诊断性检验主要是检验模型的有效性。一个模型是否显著有效主要看它提取的信息是否充分。一旦观察值序列中蕴含的相关信息充分提取出来了，那么剩下的残差序列就应该呈现出纯随机的性质。如果序列值彼此之间没有任何相关性，那就意味着序列是一个没有记忆的序列，过去的行为对将来的发展没有丝毫影响，这种序列称为纯随机序列。从统计分析的角度而言，纯随机序列是没有任何分析价值的序列。换言之，拟合模型的残差序列为白噪声序列时，这样的模型称为显著有效模型。

对模型进行Ljung-Box检验，给出自由度为21的卡方值为14.464，得到P值为0.8489。在显著性水平取为0.05的条件下，检验统计量的P值很大，说明序列已经不存在相关信息，可以视为白噪声序列，进一步表明此模型已充分捕获了时间序列中的依赖关系。

进一步，对残差进行Shapiro-Wilk检验，得到的统计量为0.9921，对应的P值为0.6643，在5%甚至1%的显著性水平下，都不能拒绝零假设，说明残差项的正态性通过了检验。

五、预测

通过前文对社会消费品零售总额数据的平稳性分析和模型拟合，以及模型诊断与评价，确定最终模型为ARIMA（0，1，1）×（0，1，2）12模型。之后，利用该模型对2017年12月至2018年12月社会消费品零售额进行外推预测，预测的结果如表3所示。

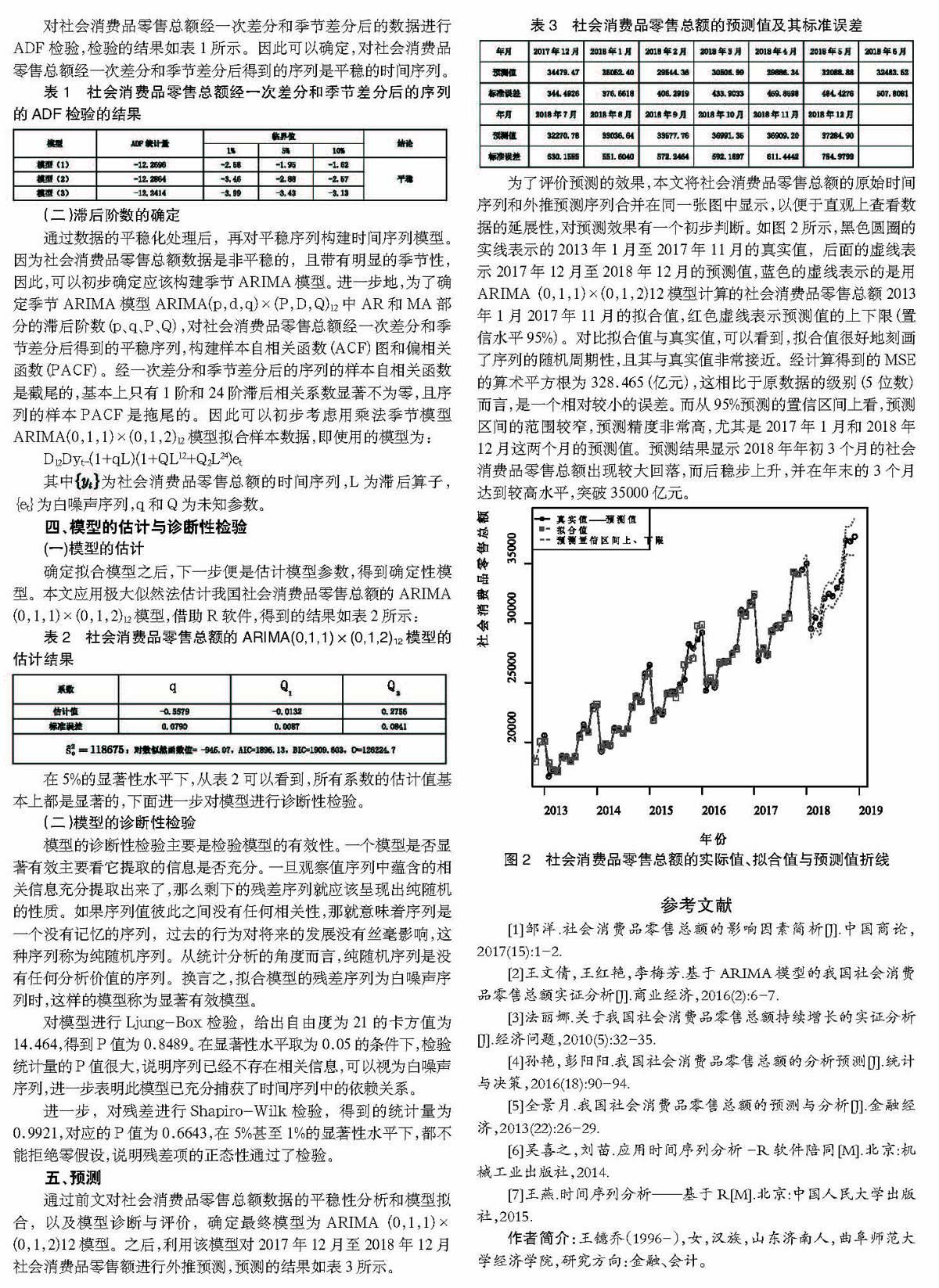
为了评价预测的效果，本文将社会消费品零售总额的原始时间序列和外推预测序列合并在同一张图中显示，以便于直观上查看数据的延展性，对预测效果有一个初步判断。如图2所示，黑色圆圈的实线表示的2013年1月至2017年11月的真实值，后面的虚线表示2017年12月至2018年12月的预测值，蓝色的虚线表示的是用ARIMA（0，1，1）×（0，1，2）12模型计算的社会消费品零售总额2013年1月2017年11月的拟合值，红色虚线表示预测值的上下限（置信水平95%）。对比拟合值与真实值，可以看到，拟合值很好地刻画了序列的随机周期性，且其与真实值非常接近。经计算得到的MSE的算术平方根为328.465（亿元），这相比于原数据的级别（5位数）而言，是一个相对较小的误差。而从95%预测的置信区间上看，预测区间的范围较窄，预测精度非常高，尤其是2017年1月和2018年12月这两个月的预测值。预测结果显示2018年年初3个月的社会消费品零售总额出现较大回落，而后稳步上升，并在年末的3个月达到较高水平，突破35000亿元。

参考文献

[1]邹洋.社会消费品零售总额的影响因素简析[J].中国商论，2017（15）：1-2.

[2]王文倩，王红艳，李梅芳.基于ARIMA模型的我国社会消费品零售总额实证分析[J].商业经济，2016（2）：6-7.

[3]法丽娜.关于我国社会消费品零售总额持续增长的实证分析[J].经济问题，2010（5）：32-35.

[4]孙艳，彭阳阳.我国社会消费品零售总额的分析预测[J].统计与决策，2016（18）：90-94.

[5]全景月.我国社会消费品零售总额的预测与分析[J].金融经济，2013（22）：26-29.

[6]吴喜之，刘苗.应用时间序列分析-R软件陪同[M].北京：机械工业出版社，2014.

[7]王燕.时间序列分析——基于R[M].北京：中国人民大学出版社，2015.

作者简介：王镱乔（1996-），女，汉族，山东济南人，曲阜师范大学经济学院，研究方向：金融、会计。