多元化思维在中职数学解题中的应用研究

李一奇

(江苏省如东中等专业学校 226400)

一、多元化思维及其在中职数学解题中的地位和作用

第一，多元化思维就是从不同角度和各个方面看待问题和思考事物的综合性思维过程，它与单一思维相对应，注重从全方位、多角度看待事物和解决问题，是帮助人获得更多选择方式和余地、产生新思路、避免走进死胡同、寻找最优解决方案的有效方式.

第二，有助于帮助学生从不同的角度、用不同的方法思考和解决数学问题，提高数学成绩.数学是一门十分锻炼和提升人的思维能力的学科，运用不同的思维方式分析和解决数学问题，能够帮助学生更加灵活地掌握和运用数学知识与方法，提高数学成绩.

第三，有助于培养学生养成灵活的思维和思考方式.多元化思维就是从不同的角度分析和解决问题，运用多元化思维解决数学问题，能够培养学生运用不同方法和途径解决数学和其他课程学习过程中遇到的问题的能力，培养学生养成全面思考问题的习惯，能够从多种方案中选择出解决问题的最佳方式.

二、多元化思维在中职数学解题中的实际应用

数学解题中用到的解题思维方式多种多样，比较常见的有转化思维、整体思维、逆向思维、数形结合等数十种思维方法.笔者以转化思维和逆向思维为例，分析多元化思维在中职数学解题中的运用.

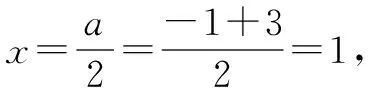
第2，转化思维.转化思维是几乎每一道数学题都会用到的解题思路，它指的是转化和归结两种解题思维的简称，也称化归思维.简单地说，化归思维就是将比较复杂的问题简单化，由繁化简，在数学的解题方法中，待定系数法、配方法和整体代入法对这种思维方式的体现最为明显.如下题：已知x,y满足x2+3x+y-3=0,求x+y的最大值.这道题求的是x+y的最大值，很明显，x和y都是已知题目中的变量，它们存在的是某种变量关系，所以要求x+y的最大值就无法使用常规的求出x和y的具体数值的方式，可以根据方程式的关系用x将y表示出来(或用y表示x)，即y=-x2-3x+3,然后简化x+y的关系式，得出x+y=-x2-2x+3=-(x+1)2+4.根据一元二次函数的性质可以得出在x取-1时，函数取最大值，即x=-1时，x+y的值最大，此时x+y=-(-1+1)2+4=4,所以这道题的最终答案为4.上面这道例题同时使用了配方法和整体代入法两种方法，鲜明地体现了转化思维在解题过程中的作用.

三、多元化思维在中职数学解题中应用的启示

第一，熟悉掌握各种解题思维的方法和内容.将多元化思维用于中职数学解题，必须明确各种思维方式的内容和要点，了解它们各自适用的解题范围和类型，这是能够对解题思维和思路做出准确判断的必要条件之一.只有了解了不同解题思维的特点，才能根据特点在解题过程中选择正确的解题方法.

第二，掌握坚实牢固的基础知识.多元化解题思维的运用要以深厚的基础知识积累为依托，思维方式只是为解题者提供大致的思考方向，它既适用于数学学科，也适用于其他学科，所以，多元思维在具体学科中的运用还需要对这一学科的各项知识有深厚的积累.对中职数学的解题，要准确迅速地找出解题方法，除对各种思维方式的了解外，也需要掌握大量的数学基础知识(如概念、性质、画图技巧等).

第三，增强练习强度.很多中职学校学生的数学基础比较薄弱，对很多知识都处于一知半解的状态，需要在课前和课后通过大量的练习和精力投入才能弥补回来.而且，对不同解题思维和解题方法的熟练掌握，需要练习者不断通过练习和实践积累来完成.所以，对中职数学的实际教学和学生学习情况来说，要实现多元思维在解题过程中的熟练运用，必须通过大量的实践练习来实现.

多元思维是运用不同思维方式看待事物和解决问题的一种思维方式，它追求在最短时间内寻求最优的解决方式.多元思维在中职数学解题中的运用十分广泛，它对于提高学生的解题效率和思维灵活性具有重要作用.在运用多元思维进行中职数学的解题时，需要掌握更多的思维方式、数学学科的基础知识，而达到熟练运用的目的，还需要学生们通过勤奋不辍的练习才能实现.