A Memory-efficient Simulation Method of Grover’s Search Algorithm

Xuwei Tang , Juan Xu, and Bojia Duan

Abstract: Grover’s search algorithm is one of the most significant quantum algorithms,which can obtain quadratic speedup of the extensive search problems. Since Grover's search algorithm cannot be implemented on a real quantum computer at present, its quantum simulation is regarded as an effective method to study the search performance.When simulating the Grover's algorithm, the storage space required is exponential, which makes it difficult to simulate the high-qubit Grover’s algorithm. To this end, we deeply study the storage problem of probability amplitude, which is the core of the Grover simulation algorithm. We propose a novel memory-efficient method via amplitudes compression, and validate the effectiveness of the method by theoretical analysis and simulation experimentation. The results demonstrate that our compressed simulation search algorithm can help to save nearly 87.5% of the storage space than the uncompressed one. Thus under the same hardware conditions, our method can dramatically reduce the required computing nodes, and at the same time, it can simulate at least 3 qubits more than the uncompressed one. Particularly, our memory-efficient simulation method can also be used to simulate other quantum algorithms to effectively reduce the storage costs required in simulation.

Keywords: Grover’s search algorithm, probability amplitude, quantum simulation,memory compression.

1 Introduction

Quantum computation, which can accelerate a wide range of applications than their classical counterparts, has attracted much attention for the last three decades [Feynman(1982); Nielsen and Chuang (2000)]. Quantum computation has been applied to various fields, including quantum key agreement (QKA) [Liu, Chen, Ji et al. (2017); Liu, Xu,Yang et al. (2017)], quantum sealed-bid auction (QSA) [Liu, Wang and Yuan (2016); Liu,Wang, Ji et al. (2014)] and quantum machine learning [Lloyd, Mohseni and Rebentrost(2013)]. Notable among the quantum algorithms, Grover’s search algorithm can achieve quadratic acceleration on search applications over unstructured data [Grover (1999)].

There have been a wide range of generalization and applications of the algorithm, solving problems like pattern classifications and weight decision problem [Singh (2014); Uyanik and Turgut (2013); Yoder, Low and Chuang (2014)]. For the sake of proof of principle,implementation of the algorithm can be achieved via nuclear magnetic resonance,trapped-ion system, cavity-QED and so on [Araujo-Ferreira, Brasil, Soares-Pinto et al.(2012); Ivanov, Ivanov, Linington et al. (2010); Waseem, Ahmed, Irfan et al. (2013)].But those methods cannot be scalable for large qubits now.

While realistic quantum computers have not been available yet, simulation on classical computers using traditional quantum circuit model can be utilized for studying and developing quantum algorithms [Karafyllidis (2005); Gutierrez, Romero, Trenas et al.(2010)]. On the supercomputer JUGENE with almost 300,000 processors, up to 42 qubits of the quantum system have been achieved [Henkel (2010)]. However, simulation of quantum circuits desires exponential memory resources, it is imperative that efficient methods should be implemented for simulating more qubits with less storage resources.To reduce the memory resources of the algorithm’s simulation, several compression methods on the storage of qubits and unitary operations were proposed. Sparse vector and matrix using a mathematica package were presented for quantum circuit simulation[Gerdt, Kragler and Prokopenya (2009)]. However, the memory resources and the calculation time have been reduced simply dramatically in terms of the sparsity of the qubit vector and unitary matrix. A saving of basis states’ number was proposed by storing the qubit states whose amplitudes are non-zeros, which has shortened the qubit state lists during the simulation to some extent [Lu, Yuan and Zhang (2013)]. Whereas the length of the state list which includes both basis states and amplitudes has still been. We have proposed a high-performance Grover’s algorithm simulation in Tang et al. [Tang,Xu and Zhou (2017)] combining the characteristics of Grover’s algorithm and the parallelism of cloud computing, which dramatically improves the performance of the load balancing among multi-core, the utilization of memory space and the efficiency of simulation.

In this paper we propose a high compressed method in the simulation of Grover’s algorithm. Draw the lessons from the compressed methods recommended in Plattner et al.[Plattner and Zeier (2012)], we analyzed the duplication of the probability amplitudes along the process of the computation in the algorithm, and calculated the number of no duplicate probability amplitudes (NDPA) at each computational step, with the result showing that the maximal number is 7. Applying this result, the amplitudes vector length in the state list can be sharply reduced to 7 rather than. And the efficiency of the Grover simulation algorithm has been improved significantly.

This paper is organized as follows: Notations and a brief overview of Grover’s algorithm is given in Section 2. In Section 3, the NDPA theorem in the context of single solution of Grover’s algorithm is proposed with the proof process followed. Then we illustrate the high compressed simulation method using NDPA theorem in Section 4 and state the experiments on quantum simulation and analyze the results and performance of simulation in Section 5. Finally, the conclusion is drawn in Section 6.

2 Background

The related notations will be firstly discussed. The superposition ofqubits, i.e., is labeled as a probability amplitude vector:,whereandrepresent the basis state and the relevant probability amplitude respectively. Furthermore, two functions are involved here. The function unique(amp)returns a vector containing no duplicate probability amplitudes (written as NDPA vector)in amp. And the function unique_num(amp) returns the number of elements in unique(amp) (written as NDPA number).

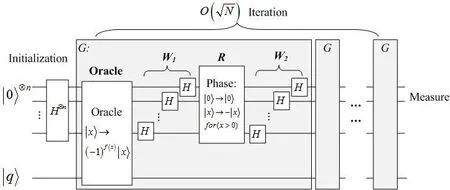
Figure 1: Circuit frame of Grover algorithm

Let us simply remind the readers of the process of Grover search algorithm [Grover(1999)]. This algorithm employs pure states of n qubits which is initialized to the superposition of all computational basis states. Then the Grover iteration can be divided into four stages which are labeled as Oracle,,and, and the quantum circuits are illustrated in Fig. 1. Finally, the final measurement of the external system is followed.Oracle: Applying Oracle to recognizing the solution, and it can be simple expressed as

Repeating the Grover iteration abouttimes we can obtained solutions with a high probability when the first quantum bits are measured. For a more intuitive and clearer understanding of Grover algorithm in geometry, we assume thatis the set of non-solutions, andis the set of solutions. Then assume

The initial state can be written as

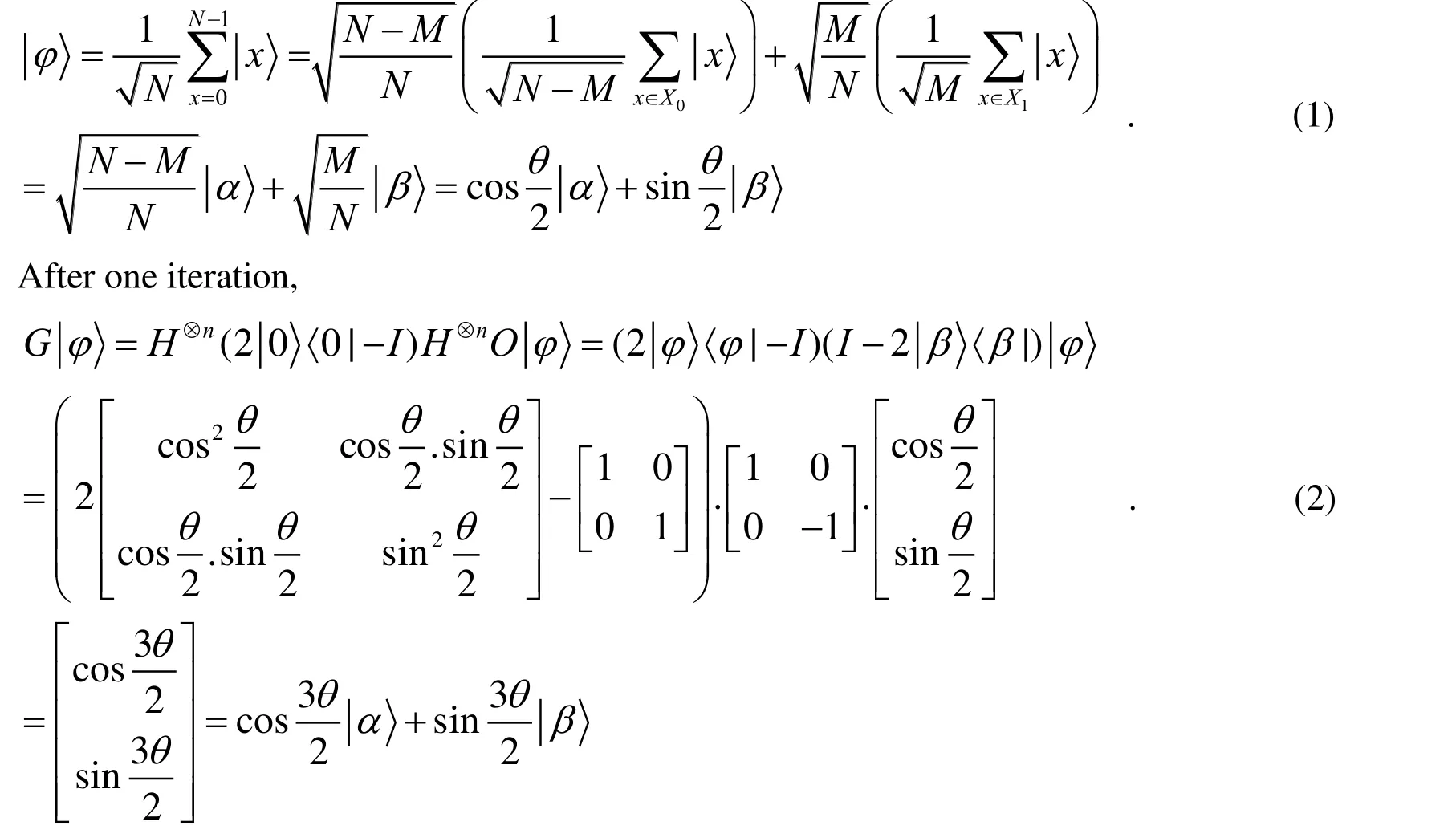
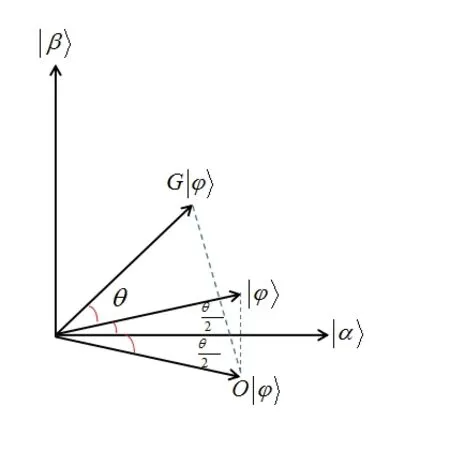
Figure 2: The action of a single Grover iteration G (In the figure all states are unit vectors. In order to show the action of G clear,and are lengthened a little)

It can be seen in Fig. 2 that the vectoris rotated bytowards the superpositionof all. Thus by performing about R Grover iterations, rotatewithin an angleof. And then obtaining the solutions is with very high probability through measuring.During the iteration, the Oracle qubit[Trieu (2009)] initially prepared in the stateis used for marking the target basis state. Assume thatis on the highest order of all qubits, making each probability amplitude satisfy the following equation:

To simplify the process of the proof, we can make an appointment of omitting Oraclequbit in stages and of the proof, i.e. we can just consider the condition for the firstbasis states, where the latterbasis states are exactly the opposite of the first ones.

3 Probability amplitudes analysis of Grover’s algorithm

Quantum simulation has become the main method of current quantum theory research,but insufficient memory is the primary factor limiting the simulation to continue. In order to solve this problem, we present a memory-efficient simulation method. The theorem which is named as NDPA theorem is the soul of the memory-efficient simulation method.We explore the statistics of the probability amplitudes of Grover’s algorithm, and propose the NDPA theorem in the context of single solution.

Theorem. The maximal NDPA number is seven after each step of the computation in Grover search algorithm, i.e.

3.1 Proof

The proof includes two major steps. Step I is on the analysis of the amp vector after Oracle operation of any Grover iteration, and Step II is divided into four stages according to the process of one Grover iteration which calculates the NDPA numbers. The coefficients are integer-valued by eliminating the scaling factor in the proof.

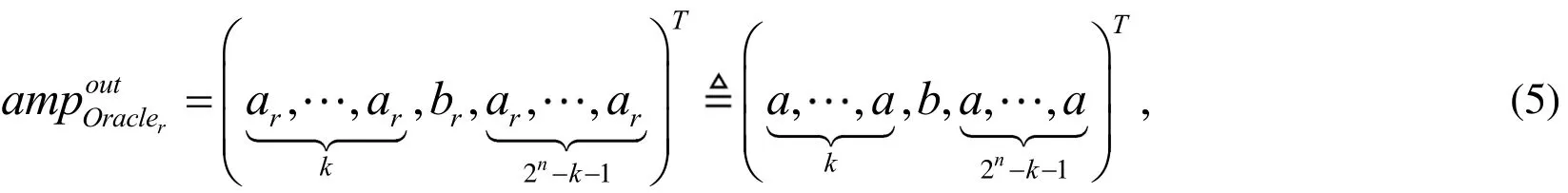
Step II: By splitting any one Grover iteration into four stages, which is illustrated in Fig.1, we will calculate the NDPA number respectively and proof that the Eq. (4) will be satisfied after each step of the computation.

(1) Referring to Grover [Grover (1999)] and Eq. (5), omitting the oracle qubit, there is

Oracle can be carried out by the following three elementary gates: Phase-X gates,control-X gates and Toffoli gates which just involve the exchange of the amplitudes of the related basis states after each step [Lu, Yuan and Zhang (2013)]. Taking on the oracle qubit, given any i , after the-th step of operation, all elements in the vectorbelong to the following set:

(2) The second stage involves n continuous Hadamard gates. Consider the process of the form W1==A1A2A3Anwith Aidenoting the Hadamard gate performed on the i-th qubit. The non-zero elements in matrix Aiare as follows:

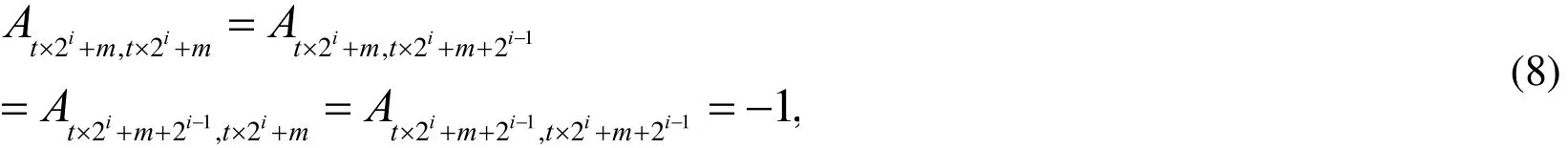
where n denotes the number of qubits, 1≤i≤n , t =0,1,2, ,2n-i- 1, m =0,1,2, ,2i-1-1.

Mathematical induction can be used to prove that the probability amplitude vector satisfies the following equation after each step of W1,

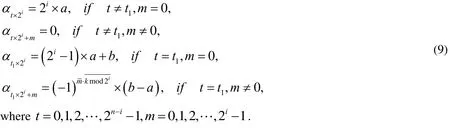
By Eq. (9), the elements in the vectorbelong to the following set:

(3) The output of the second stage is

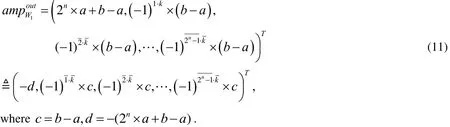
The third stage can be treated as one particular case of Oracle operation, i.e. the elementcan be regarded as the target element (up to an irrelevant global phase of -1), thus given any i, after the i -th step of operation, all elements in the vectorbelong to the following set:

(4) Similarly to the second stage, mathematical induction can be used to prove that the probability amplitude vector satisfies the following equation after each step of ,

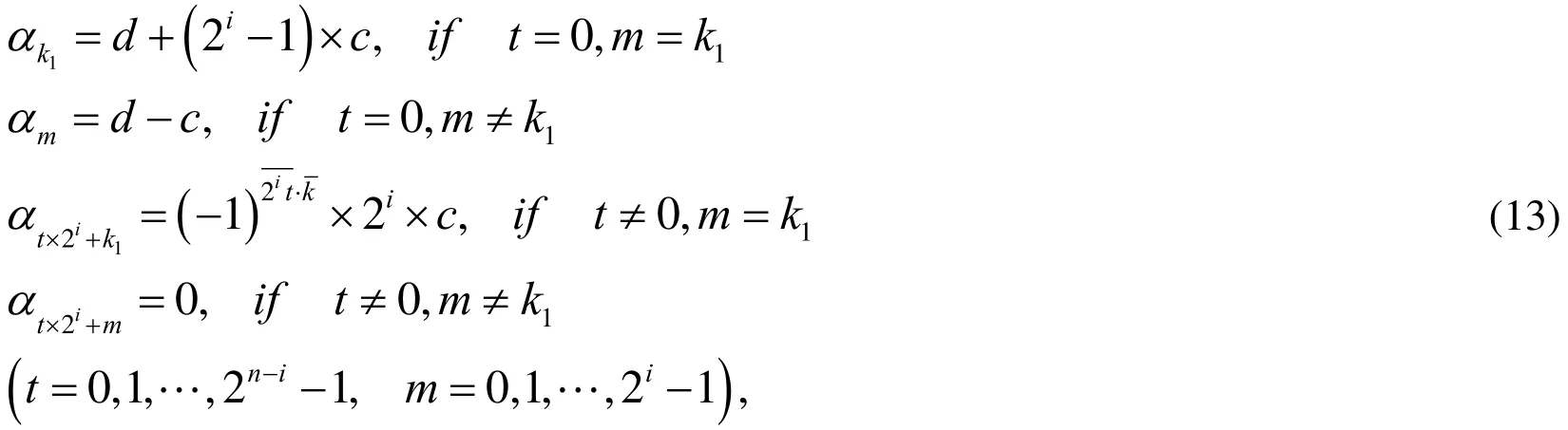
By Eq. (13), the elements in the vectorbelong to the following set:

After the calculation of the NDPA vectors, we should also analyze the situation in the present of the Oracle qubit in stage II and IV. As is illustrated in Tab. 1, the first column expresses the operation stage of Grover iteration. The second column lists the amplitudes sets with no duplicate elements of the firstbasis states, while the corresponding equations are showed in the sixth. Then Eq. (3) and the second column give the amplitudes sets with no duplicate elements of the lastbasis states, which are shown in the third column. By the union operation of the front two columns, we get the sets in the fourth column and the relevant numbers in the fifth column. Obviously, the Eq. (4) is satisfied according to the numbers in the fifth column. Now the proof of the NDPA theorem is completed.

Table 1: Unique numbers of amplitudes analysis in Grover iteration

3.2 Verification

We verified the theorem on MATLAB. In the program, a float array amp[] is used to store the probability amplitudes in one Grover iteration; the function unique() returns an array representing NDPA vector and the integer array uni_num[] denotes the NDPA numbers along the whole computational process in which each data stores the length of unique(amp). The major corresponding pseudo code is as follows.

UNIQUE_NUMBER(AMP)

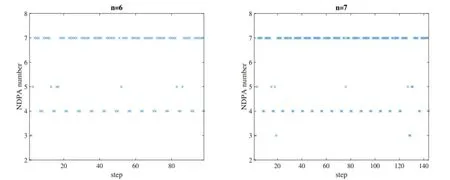
Figure 3: NDPA numbers along the whole computational process in Grover’s algorithm

Fig. 3 shows the behavior forandwhere we can easily observe that the maximal NDPA number is seven, i.e. the theorem is valid.

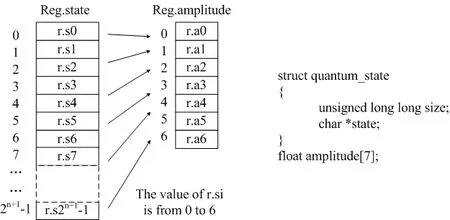
Figure 4: Structure of the node type including state and amplitude

4 The memory-efficient simulation method

In this section we apply the theorem to quantum simulation of Grover algorithm for the purpose of compressing the memory size by developing a C program. As in the original method, the state list and amplitude list are both stored exponential whose maximal length is. Applying the NDPA theorem, the size of amplitude list can shrink to a constant. The relevant data structures in our program are shown in Fig. 4, where we use a seven-length list to store the unique amplitude at a single step along the algorithm. The key procedures of our program are depicted in Fig. 5(a), which serve to detail the compressed simulation method. The program begins with initialization of the amplitude list and the state list. Along the whole process of simulation algorithm, the quantum gates are performed one after another until the final iteration is over. Only the Hadamard gate involves amplitude updating procedure. Then the state list storing the index of the amplitude refreshes and a round of the quantum register updating after quantum gate operation is finished.

Furthermore, we detail the amplitude updating procedure, depicted in Fig. 5(b). An amp_temp list is initialized for storing the amplitudes after gate operation. If any computed amplitude data do not exist in the amp_temp list, the new data will be added to the amp_temp list. Then the program updates the state list with the new index of the amplitude. All basis states’ index numbers will be refreshed before the procedure is over with the help of an auxiliary list marking the basis state calculated.

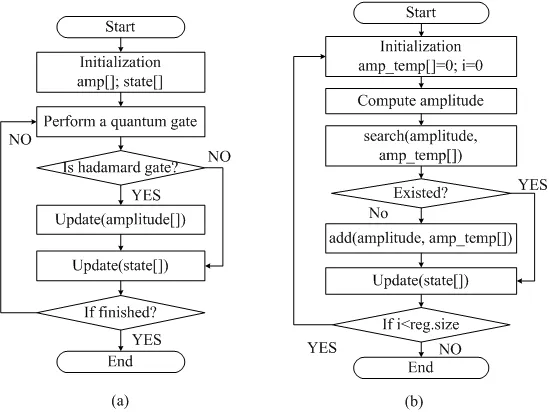
Figure 5: (a) Flowchart overview of the main procedure. (b) Flowchart overview of the amplitude updating procedure

Now the compression ratio can be effortlessly figured out by theoretical analysis. For the uncompressed method, the state list stores 8 bytes which type is unsigned long long int fortimes, the amplitude list stores as float_complex type needing 8 bytes fortimes. Thus, the complete storage space for the uncompressed list is now:

In comparison, for the compressed method, the state list (Reg:state) stores the location substituted for the numerical value of the corresponding amplitude fortimes, i.e. the value range of the elements in Reg:state list is from 0 to 6, so 1 byte is sufficient for storing one location of the amplitude; and the amplitude list stores as float_complex type for only 7 times. Here we also need another byte as auxiliary to label the calculated state fortimes and a temporary amplitude list for calculation. Thus the complete storage space for the compressed list is now:

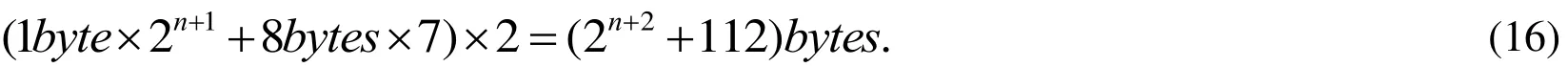
Table 2: Memory of LQ and CG programs with different qubits

5 Experiments and analysis

The experiments reported in this paper were performed on an Intel Xeon E5506 CPU with 4 cores at 2.13 GHz clock rate, 47.2 GiB of memory. The hardware platform may restrict the performance of the experiments, however, the trends in time and memory size can be seen from the results reported below. We have also run the libquantum1.1.1 program for comparison [Weimer (2013)]. The two programs we implemented are itemized as follows:

● Libquantum (LQ): The serial code of the Grover algorithm executed is from the libquantum library, according to the release of libquantum1.1.1 [Weimer (2013)].

● Compressed_Grover (CG): The algorithm is simulated according to the method described in Section 4.

We compare the time consumption of LQ and CG and analyze the complexity of simulation process. We set the network delay as δand the communication consumption between processes is kω(where kis the number of nodes). As the number of qubits is large enough the extra-cost Δextra= kω+δcan be approximated by a constant, so there is a little difference between the time efficiency of LQ and CG.

For verifying the result on the basis of the experiment data, Tab. 2 compares the memory cost of the two programs. Interestingly, although CG program compress the length of amplitude list fromto 7, the trends of the total memory cost of the two programs both grow exponentially with the number of qubits n, which is for the reason that the storage of the basis states list increases exponentially with the qubits. Moreover, it is clear that 3 more qubits can be simulated in CG program than in LQ program base on the same storage memory. Taking 256 MB memory for example, 26 qubits can be simulated in CG program, while in LQ program, only 23 qubits can be implemented. Furthermore,8 or more computing nodes will be needed to simulate 31 qubits in LQ program, but only one computing node is needed in CG program. The result shows that the compression method is effective, which helps saving nearly 87.5% memory when n is infinity.

6 Conclusion

In summary, we have proposed an efficient simulation method of Grover’s search algorithm in the context of a single solution. In particular, we proposed a theorem showing that the storage of the probability amplitudes can be compressed to a constant which is independent of the number n of qubits for large n. We have also applied the theorem to the simulation of Grover’s algorithm based on the classical computers, and the results show when nis infinite 87.5% memory can be saved and three more qubits can be simulated in the same storage space. In the future work, this work can be used in the simulation on General Purpose GPU and more qubits can be simulated. In addition, the memory-efficient simulation method of Grover’s search algorithm we proposed will be used to optimize the training process of support vector machine and relevance vector machine.

Acknowledgement:This work was supported by Funding of National Natural Science Foundation of China (Grant No. 61571226, Grant No. 61701229).