基于FTA的贝叶斯网络变送器可靠性评估
2018-11-28张轩雄
蒋 芹,张轩雄
(上海理工大学 光电信息与计算机工程学院,上海 200093)
传统的系统可靠性研究方法过于单一,难以直观展现出复杂系统各故障间的相互联系。故障树分析(Fault Tree Analysis,FTA)是研究系统可靠性的一种有效方法。文献[1]利用FTA深入分析了蓄电池和电动车系统潜在的故障,为电动车的实用性设计提供了改进。但是FTA自身也有很多不足之处,例如无法反映各事件之间的相关性及定量阐述中间事件对故障的影响程度[2]。近些年发展起来的贝叶斯网络(Bayesian Network,BN)分析方法同时具备了正向推理与反向推理的能力,不仅可用于可靠性评估,还可用于系统故障诊断,能够有效弥补FTA应用中的不足。
变送器广泛应用于化工、石油化学和海上勘探等场所,具有体积小、探测灵敏度高、可靠性强,安全耐用、安装方便等优点,其可靠性得到各工业部门的广泛关注[3]。本文以变送器为算例进行分析,将FTA和贝叶斯网络模型结合起来用于评估液位变送器的可靠性,以此来验证基于FTA的贝叶斯网络在可靠性评估方面的有效性。
1 贝叶斯网络
条件概率是贝叶斯网络的理论基础[4],条件概率定义如式(1)所示
(1)
式中P(A|B)为释然率,P(A)为先验概率,P(B|A)为后验概率。式(2)为相应的全概率计算式
(2)
基于条件概率和全概率公式推导出相应的贝叶斯公式,贝叶斯公式事件形式为:假设B1,…,Bn是E的一组互不相容的完备事件,并且P(Bi)>0,A是E的任意事件,则称式(3)为贝叶斯公式[5]
(3)
贝叶斯网络又称为信度网络,是对概率关系的有向无环图的描述,它使用简单的图形化方法定性表示事件之间的复杂因果关系以及变量之间的条件独立性。贝叶斯网络是由一些变量的节点以及连接这些节点的有向边组成,网络中的每一个节点代表系统中用有向边连接起来的每一个变量,其中有向边代表变量之间的相互关系(即诱发事件发生的概率)[6-8]。贝叶斯网络的拓扑结构通常是根据具体的模型建立起来的,简单的贝叶斯网络模型如图1所示,在给定A1的情况下,变量A2和A3是条件独立的,即P(A2|A1,A3)=P(A2|A1)。
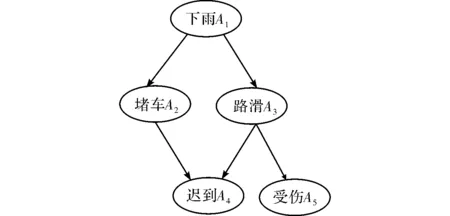
图1 贝叶斯网络的简单模型
2 变送器的故障树模型
以KSR-1001浮球液位变送器为模型做算例分析,浮球液位变送器的主要功能是根据浮力原理,采用三线式分压器对液位进行测量及信号变送。浮球内部磁钢的磁力线穿过变送器的导管,用于感应导管内部干簧与电阻链的变化而形成的阻值变化,由于干簧与电阻链排列的非常紧密,因而电压近似连续变化。浮球液位变送器的结构如图2所示。
建立FTA模型的基本原理是把所研究的系统中最不愿意发生的事件作为基本出发点,在系统中寻找直接导致这一事件发生的所有因素[9-12]。根据浮球液位变送器的功能和原理图将浮球液位变送器分成两大模块,即传感器模块和变送器模块,这两大模块也是FTA模型第一层事件。系统中任何一个模块失效都会导致系统失效,所以这两大模块通过或门连接至系统。以第一层的基本事件作为出发点,推理出导致第一层事件发生的基本事件。根据液位变送器使用厂家提供的近5年的失效数据可知,导致变送器模块失效的主要原因有接线盒进水短路、电路板焊接松动和调节模块失效等,这些事件通过或门连接至变送器模块。造成传感器模块失效的重要原因有干簧损坏、浮球损坏、电阻链损坏和主管进水等事件,也是通过或门连接至传感器模块。依次建立的变送器FTA模型如图3所示。

图2 浮球液位变送器原理图
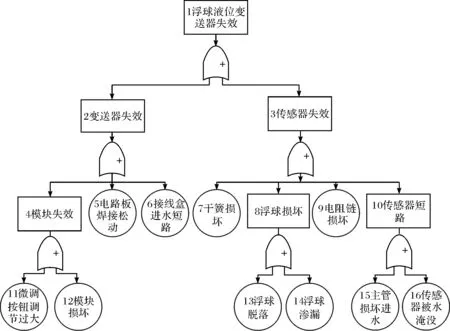
图3 浮球液位变送器故障树
3 变送器可靠性分析
3.1 基于FTA的贝叶斯网络
将故障树模型转换为贝叶斯网络模型,首先应当考虑如何将逻辑门关系转换为相应的贝叶斯网络的结点和条件概率分布表(Conditional Probability Table,CPT)。在变送器的可靠性评估中,贝叶斯网络模型的建立是与故障树的结构一一对应的,因此基本事件应转换为贝叶斯网络的节点,将故障树中的逻辑门转换成贝叶斯网络的条件概率分布表。由此形成贝叶斯网络的映射关系应遵从以下原则:(1)故障树中的每一个根事件、中间事件以及基本事件分别映射为贝叶斯网络的根节点、中间节点和叶节点,对于多次出现的节点,在贝叶斯网络中只需要建立一个节点;(2)故障树中的逻辑门对应的输入输出关系转换为贝叶斯网络中的有向边。基于这两条原则,可将故障树模型转换为贝叶斯网络模型,浮球液位变送器的贝叶斯网络模型如图4所示。
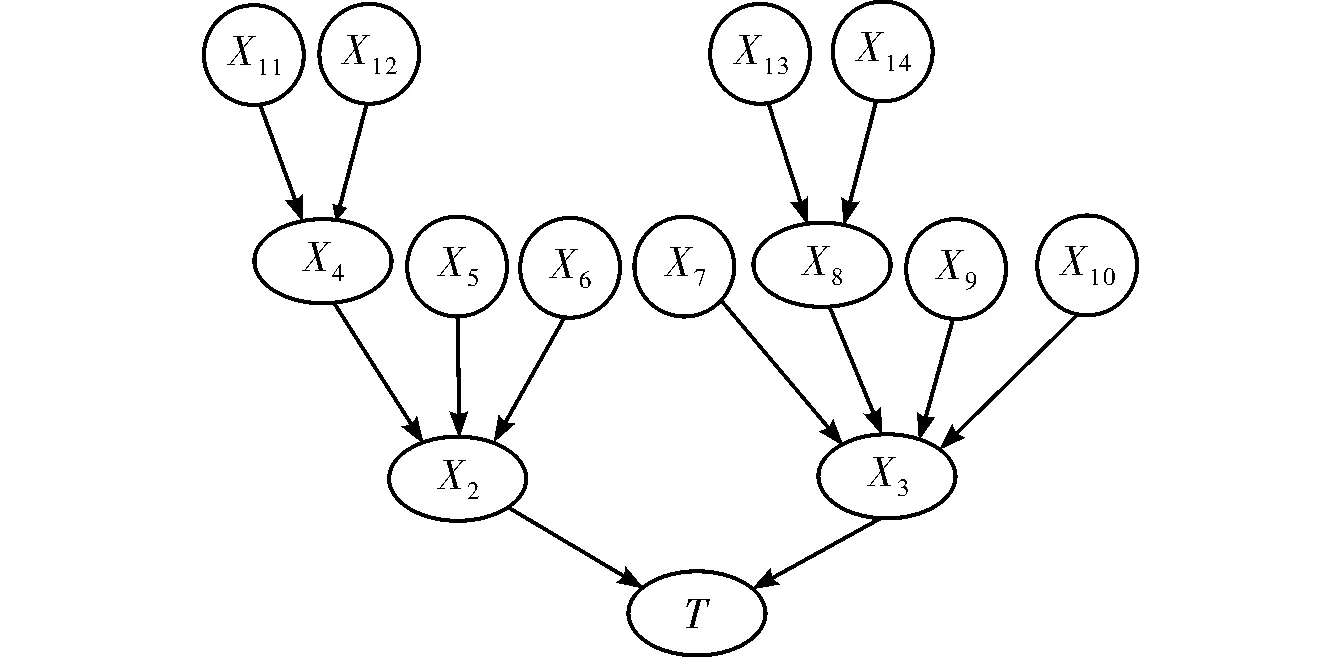
图4 贝叶斯网络模型
3.2 基于贝叶斯网络的失效率
在项目的基础上记录了浮球液位变送器近5年的失效数据,通过数据处理来获得基本事件的失效率。因为失效率主要考虑的内容是失效事件发生的概率,因此将失效数据中失效事件时间间隔取倒数转换为事件的失效率,处理后的失效数据如表1所示。利用贝叶斯网络精准的推理算法-桶排除方法进行可靠性计算,将所有的基本事件作为贝叶斯网络的输入变量。有向边提供了基本事件的逻辑运算准则,相应的计算公式如式(4)所示,式中Xi为中间节点或者叶节点,n为节点个数。
(4)
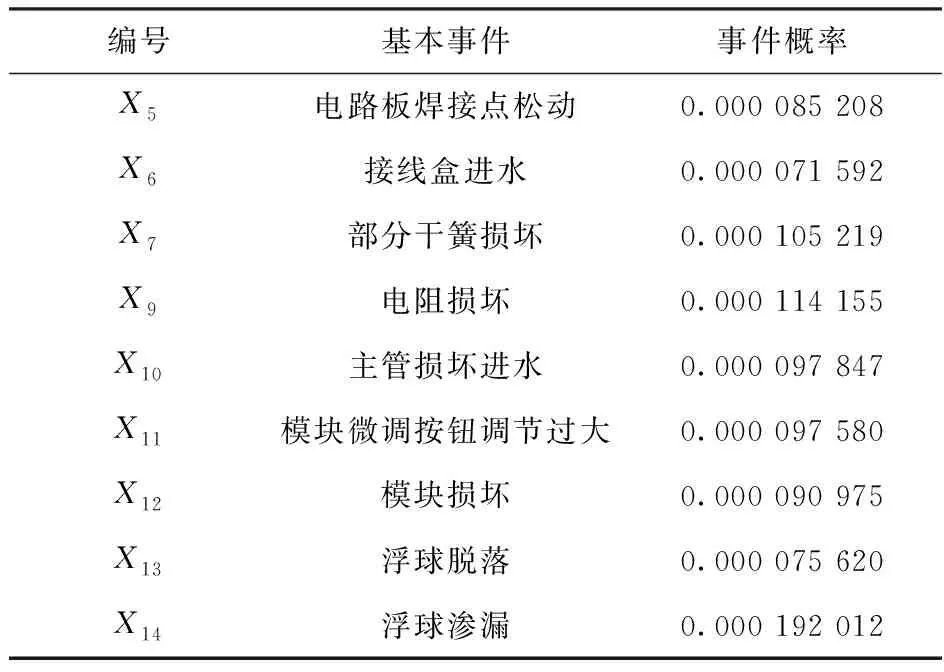
表1 基本事件的失效率
中间节点的失效率是由叶节点的失效率通过定向的逻辑关系求得的,将叶节点的失效率带入式(4),将计算式展开为式(5)来推导失效率。经计算后得到的浮球液位变送器失效概率为P(T=1)=0.000 929 859。在排除失效的前提下系统即是可靠的,浮球液位变送器的可靠度为R=0.999 070 141。
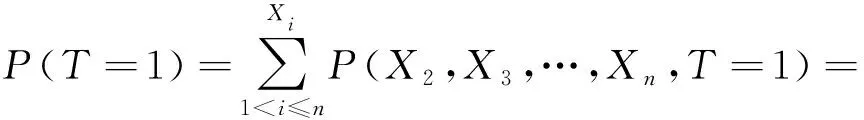
(5)
基于贝叶斯网络可靠性分析的推理方法,可以使用贝叶斯网络的桶排除法进行正向推理,得到浮球液位变送器的失效率和可靠性。而在系统失效的前提下,也可以利用后验概率得到各基本事件的发生概率,由此找出浮球液位变送器的故障元件用于系统失效时故障的排查。假设在系统故障的前提下T=1时,可由贝叶斯公式(3)计算出浮球液位变送器各个基本事件的后验概率,各个元件发生故障的条件概率如表2所示。
由表2可以看出各个元件在浮球液位变送器可靠性中所起到的重要性。浮球所处的环境温度过高或者压力过大都有可能导致浮球破裂渗漏。X14(浮球渗漏)在浮球液位变送器失效时发生故障的可能性相对最大,这与先验概率中的浮球渗漏基本事件概率为最大是一致的。X9(电阻损坏)发生的可能性也较大,浮球和电阻链都是传感器系统的重要部件,由于传感器系统一直处于动态环境中,动作频率高,因此元器件易发生损坏。
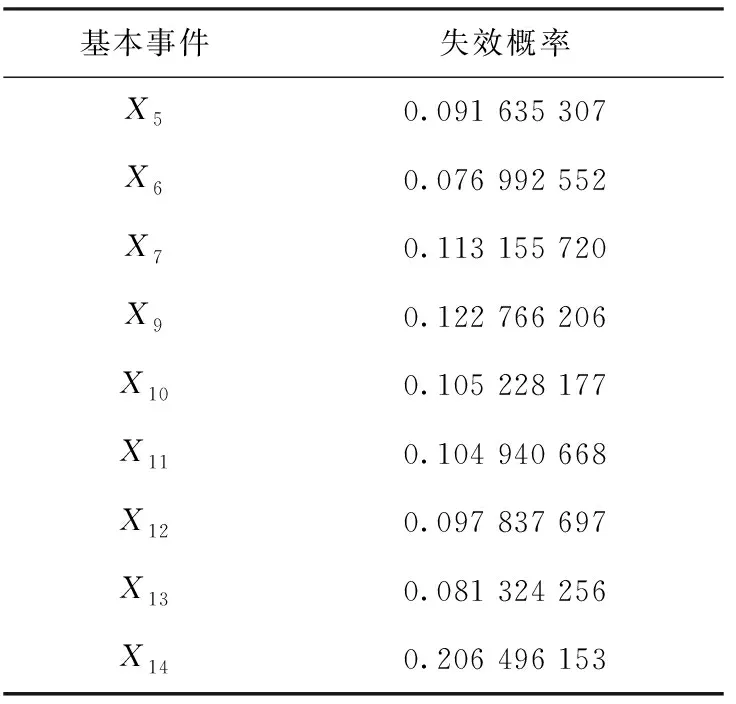
表2 系统故障时各元件故障的概率
4 基于贝叶斯网络的重要度分析
在贝叶斯网络分析中,浮球液位变送器的系统与部件、部件与部件之间的关系可以通过3种重要度数据来分析和表达,其中概率重要度和临界重要度数据最为直观。概率重要度Ig(i)主要体现FTA贝叶斯网络的底层事件概率的动态变化对浮球液位变送器可靠性的影响,如式(6)所示。式中Φ为根事件发生概率函数,Xi为顶层基本事件。临界重要度也叫做关键重要度,用于浮球液位变送器可靠性参数设计和排列诊断检查顺序表[13-16]。临界重要度的公式如式(7)所示,概率重要度与临界重要度之间的关系如式(8)所示
(6)
(7)
(8)
把基本事件的失效率代入公式,表3为经过运算得到概率重要度和临界重要度数据。由概率重要度数据可以看到,X14(浮球渗漏)事件概率的变化对液位变送器系统失效率的变化影响最大, 降低浮球的失效率将在很大程度上减少系统的失效率。浮球渗漏的临界重要度参数也比其他事件参数高出很多,在变送器的改造设计时可将浮球的可靠性参数设计的较高,以此来提高系统的可靠性。浮球渗漏、干簧损坏和电阻损坏这3个故障之间的影响较大,由于这三者均是传感器的重要部件,在浮球渗漏的情况下会产生电阻和干簧失效的恶性循环。

表3 重要度数据
5 结束语
基于FTA的贝叶斯网络模型,不仅可以对变送器的可靠性进行评估,还为评估可靠性提供了一种有效的方法,这种方法还可以应用于机械、建筑、医疗和电力等行业。通过实验分析得到出,浮球液位变送器系统的失效概率P(T=1)=0.000 929 859,可靠性R=0.999 070 141。根据IEC 61508-1:2010,IEC 61508-2:2010和IEC 61508-3:2010,浮球液位变送器属于A类子系统,系统的安全完整性等级达到SIL3。
