基于MIV-Elman神经网络的海洋生物酶发酵软测量*

孙丽娜， 邓玲黎， 刘 骏， 黄永红

(1.苏州工业园区职业技术学院 机电工程系，江苏 苏州 215123；2.江苏大学 电气信息工程学院，江苏 镇江 212013)

0 引 言

海洋生物酶发酵过程具有非线性和时变性的特点，由于受市场上检测装备和技术的束缚，其发酵过程的关键生物参数，如基质浓度、菌体浓度、产物浓度很难及时在线测量，致使对整个发酵过程进行优化控制变得十分艰难，解决上述问题的有效途径之一是软测量技术[1～6]。

在软测量建模中，大多采用静态前馈神经网络，如反向传播(back propagation,BP)神经网络、径向基函数(radial basis function,RBF)神经网络[7,8]。由于海洋生物酶发酵过程具有高度时变性、非线性，若用静态前馈神经网络对一个动态的发酵过程进行辨识，就将动态建模问题转换为静态建模，使得预测精度较差。Elman神经网络可使系统具有顺应时变特性的能力，能够直接动态反映动态过程系统的特性[9,10]。另外，在软测量建模过程中，辅助变量的选择也是非常重要的，若将一些不重要的自变量引入神经网络，会使模型的精度降低。平均影响值(mean impact value，MIV)认为是在神经网络中评价变量相关性最好的指标之一[11,12]，为此，本文提出一种基于MIV-Elman神经网络的软测量建模方法，即结合Elman神经网络应用MIV方法进行变量筛选，找到对主导变量有较大影响的输入项作为Elman神经网络的输入，关键生物参数作为Elman神经网络的输出，建立了MIV-Elman神经网络软测量模型。结果表明构建的软测量模型结构简单，建模精度高，实用性好。

1 MIV-Elman神经网络原理

1.1 Elman神经网络

Elman神经网络的输入层、隐含层(中间层)和输出层的连接和前馈网络基本一致，承接层用来记忆隐含层单元前一时刻的输出值并返回给网络的输入，其结构如图1所示。

图1 Elman神经网络模型

1.2 MIV算法筛选网络变量

对n维自变量X，进行m次观测，得到向量空间X=(x1,x2,…,xm)T，与每个样本点所对应的因变量可以写为Y=(y1,y2,…,ym)T。以X作为Elman神经网络的输入，Y作为Elman神经网络的输出，进行网络学习，保存训练好的网络参数。将X进行如下变换，得到具有2i(i=1,2,…,n)个元素的向量空间

(1)

重新将式(1)作为训练好的Elman神经网络的输入，其输出为样本点中第i(i=1,2,…,n)个变量指标变化时与之对应的2n个输出向量

(2)

(3)

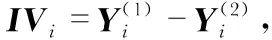
(4)

式中MIVi为变化样本中第i变量指标对输出结果的平均影响值，i=1,2,…,n，其符号代表自变量与因变量相关的方向，绝对值大小代表自变量对因变量影响的相对重要性。

2 MIV-Elman模型的建立及仿真验证

2.1 模型的建立

以典型的海洋生物酶—海洋蛋白酶为例，选择菌体浓度X、基质浓度S、相对酶活P作为软测量模型的主导变量，即Elman神经网络的输出。通过剖析发酵过程中菌体细胞生长代谢的进化过程，考虑将空气流量l，温度t，搅拌转速r，pH值，发酵罐压力p，溶解氧浓度Do，反应器体积v，基质进给速率u，CO2浓度作为软测量模型的最初辅助变量，即Elman神经网络的输入。

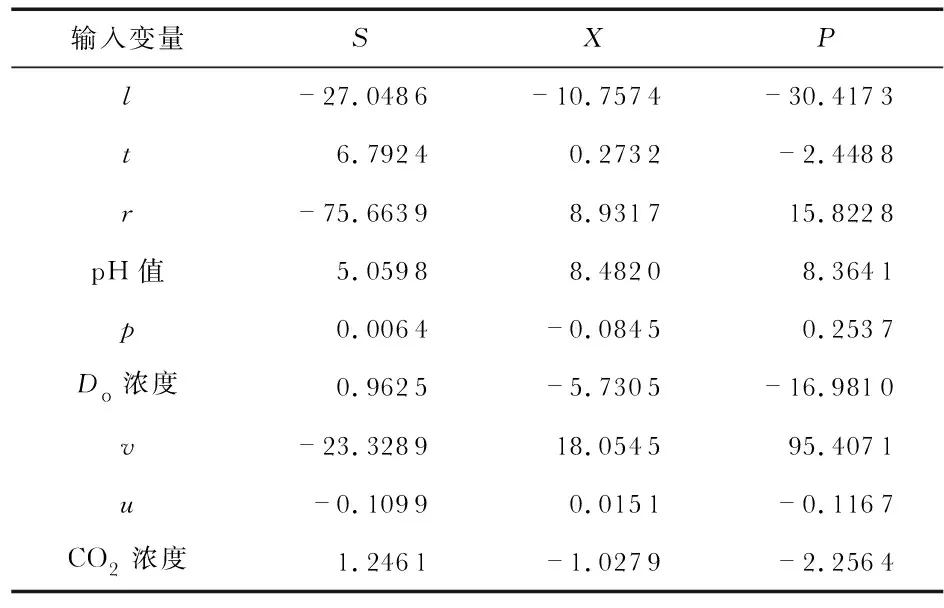
表1 输入变量的MIV计算结果

由表1可知，各个输入变量对输出变量的影响权重不一致。l,t,r,pH值,v对基质浓度影响很大，其中l,r,v与基质浓度呈负相关。l,r,pH值,Do浓度,v对菌体浓度和相对酶活的影响很大，l,Do浓度与菌体浓度和相对酶活呈负相关。其余输入变量相对于以上变量的权重值而言显得非常小，几乎可以忽略不计。

综合以上筛选结果，结合海洋蛋白酶发酵过程的机理分析，确定以l,r,pH值,Do浓度,v作为软测量模型最终的辅助变量，即Elman神经网络的输入；菌体浓度X、基质浓度S、相对酶活P作为软测量模型的主导变量，即Elman神经网络的输出。由于采集到的样本数据变化范围较大，需要利用premnmx()函数对样本数据进行[-1,1]归一化处理。在MATLAB环境下，用newelm()函数建立网络，主要参数设置：隐含层神经元传递函数设置为S型正切函数tansig，输出层神经元传递函数设置为线性函数purelin，网络的训练函数采用贝叶斯正则化算法trainbr[13]。设置最大训练次数为1 000，训练误差为0.000 1。通过结合隐含层节点选择的原则以及试验凑试法，寻找最佳隐含层节点数，最终确定隐含层节点数为20，即网络结构为5—20—3。

2.2 仿真验证

为了检验本文所提出的MIV-Elman神经网络软测量模型的有效性，用第10个批次的数据作为测试样本集对软测量模型进行验证。并与Elman神经网络(网络输入变量为表1中的9个变量，隐含层节点数为16，输出层节点数为3，其余参数设置与MIV-Elman神经网络相同)，RBF神经网络(输入输出变量与Elman神经网络相同，网络设计函数为newrb()，均方误差目标设置为0.000 1，径向基函数的扩展常数设置为0.7)，BP神经网络(输入输出变量与Elman神经网络相同，网络构建函数为newff(),隐含层节点数为20，网络训练函数采用Levenberg_Marquardt算法trainlm，隐含层与输出层神经元传递函数与MIV-Elman神经网络相同)进行了对比。

从图2中可以看出，MIV-Elman神经网络的软测量值能很好的逼近基质浓度S、菌体浓度X、相对酶活P的真实值(离线化验值)，曲线基本重合，这说明MIV-Elman神经网络软测量模型有很好的逼近非线性函数的能力，具有很高的预测精度，明显满足海洋生物酶发酵过程中关键生物参数的测量要求。

图2 软测量值和离线化验值比较

表2中采用平均绝对误差(mean absolute deviation,MAD)和均方根误差(root mean square error,RMSE)这两个预测性能的评价指标来反映模型的预测效果。

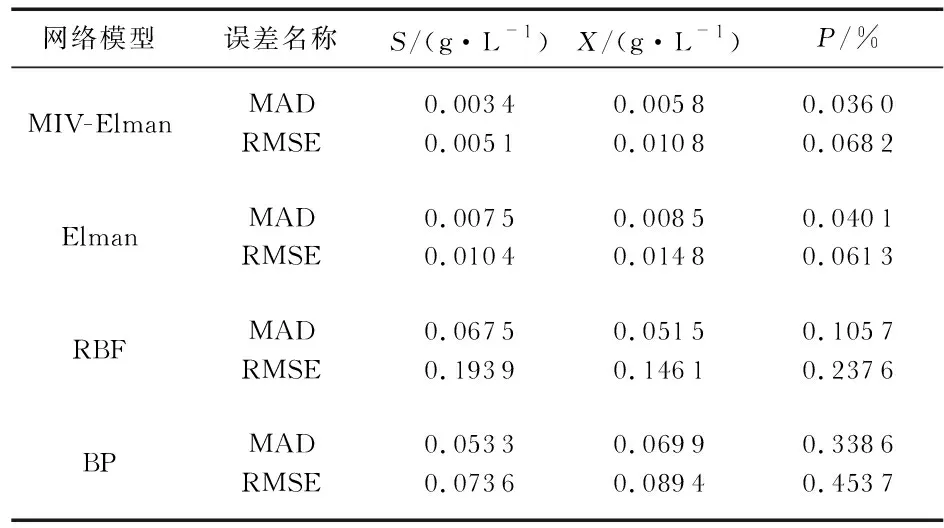
表2 预测误差

从表2中可以看出，对于基质浓度、菌体浓度来说，MIV-Elman神经网络软测量模型的MAD和RMSE比Elman神经网络的小，对于相对酶活而言，虽然MIV-Elman神经网络软测量模型的RMSE和Elman神经网络的相差不大，但MIV-Elman神经网络软测量模型的MAD比Elman神经网络的小，这验证了MIV-Elman神经网络变量筛选的有效性。

图3～图5可以看出，MIV-Elman神经网络和Elman神经网络软测量模型的预测误差比RBF神经网络和BP神经网络小的多，这说明由于Elman动态回归神经网络能直接动态反映动态过程系统的特性，具有适应时变特性的能力，使得Elman神经网络比静态前馈神经网络(BP神经网络和RBF神经网络)更能适用于海洋生物酶发酵过程关键生物参数的软测量建模。

图3 菌体浓度预测误差

图4 基质浓度预测误差

图5 相对酶活预测误差

3 结 论

本文将MIV和Elman神经网络相结合，提出一种基于MIV的Elman神经网络软测量建模方法，并应用于海洋生物酶发酵过程中。用预测样本进行了仿真验证，并与Elman神经网络，RBF神经网络，BP神经网络进行了比较，结果表明，MIV-Elman神经网络建模方法可以很好地筛选出对网络作用显著的变量，具有适应时变特性的能力和令人满意的预测效果。