基于多比特量化的哈希方法*

汪曙光， 苏亮亮， 王 琨， 唐 俊

(1.清华大学 合肥公共安全研究院，安徽 合肥 230601；2.安徽建筑大学 电子与信息工程学院，安徽 合肥 230601；3.安徽大学 电子信息工程学院，安徽 合肥 230601)

0 引 言

随着视频监控数据的爆炸式增长，从海量数据中获取感兴趣的信息时将面临巨大的时间与存储代价，使得传统方法(如穷尽搜索或树结构[1])无法满足现实需求。针对该问题，解决方案中基于哈希方法的近似最近邻搜索是卓有成效的一类方法，具有时间效率高、存储空间少等优点。

哈希方法通过哈希函数将原始高维数据映射到低维的二值编码空间(哈希空间)，这样不仅极大减少了存储空间的需求，而且基于二值编码的数据处理也显著降低了时间代价。通常哈希方法涉及两个步骤：投影学习和量化编码。前者是将原始数据投影到一个超平面而获得投影值，并使得原始数据的相似关系在投影空间得到保持。在前期的投影学习研究中，投影超平面的选取是随机产生的，典型代表有局部敏感哈希(locality sensitive Hashing,LSH)。与随机投影方法相比，依赖于数据的投影学习方法[2～5]既能有效减少编码长度也能显著提高检索效率和精度，通过已有研究发现，依赖于数据的投影策略常常优于随机投影。

量化过程指的是将投影阶段产生的投影值转换成二值码形式，其关键是量化阈值的获取。与投影研究相比，量化工作得到极少关注，已提出的大部分哈希方法均采用一个量化阈值来划分投影值并进行二值编码，即单比特量化(single bit quantization,SBQ)，其结果导致大量同类样本具有不同编码，进而破坏了原始的相似关系。针对该问题，学者们提出了多比特量化策[6～8]来保留原始数据的相似关系。此外考虑到不同投影维可能含有的信息量不同，已有自适应比特量化方法[9]被提出。然而上述大部分多比特量化方法是基于投值维数据来完成量化阈值的获取，但事实上，数据的投影值并不能够有效反映原始数据的信息分布。本文提出了一种新的基于马修斯相关性系数(Matthews correlation coefficient，MCC)计分与编码一致性的多比特量化方法，该方法直接利用原始空间中的数据信息来指导量化阈值的学习进而实现多比特编码，其中MCC计分能够有效应对数据不平衡问题。

1 MCC计分

1.1 MCC

MCC是衡量二分类机器学习模型性能的重要指标。MCC综合考虑了二分类的所有分类情况，即正样本被识别为正类(TP)或负类(FN)和负样本被识别为正类(FP)或负类(TN)，相对于其他度量准则，如正确率、精确度和召回率等，MCC能够更有效地应对不平衡数据问题，进而提供更加客观的分类性能评价。本文称MCC为MCC计分，即

MCC=

(1)

1.2 MCC计分

存在训练数据集X={x1,x2,…,xN}，N为数据规模，定义样本间的相似关系矩阵S

(2)

式中d(xi,xj)为样本xi和xj的欧氏距离，D为距离阈值。将X投影到一个超平面上，于是得到一组实值Y=[y1,y2,…，yN]，其中yi是xi的投影值，i=1,2,…,N。本文主要专注于数据投影后的量化编码，即利用2q-1(q≥2)个量化阈值划分单个投影维为2q个区域，使得每个投影值进入其中一个区域，利用q个比特去编码每个投影值，使得相似数据的投影值具有相似的多比特编码，反之不相似数据，则多比特编码显著不同。

为了获取有效的多比特编码，构建了MCC计分函数，具体为：利用已知量化阈值T={t1,t2,…,t2q-1}，t1≤t2≤…≤t2q-1，将投影值Y=[y1,y2,…,yN]划分到2q个区域{sec0,sec1,…,sec2q-1}，根据划分，分别计算统计量TP,TN,FP,FN，即处于同一区域内的相似样本对数目(TP)与非相似样本对数(FP)和处于不同区域内的相似样本对数(FN)和非相似样本对数(TN)，最后依据式(1)构建MCC计分。

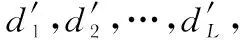
(3)

φxj计算与φxi类似,本文距离计算均采用欧氏距离。结合式(3)，TP,TN,FP,FN计算如下

(4)

式中 〈a,b〉为a与b是否相等，如果相等,返回1;否则,返回0。在上述计算中，相似关系矩阵S的对角元素不参与计算。在计算MCC计分的过程中，通常可以发现相似数据对的规模远远小于非相似数据对，而MCC计分能够有效应对种不平衡数据产生的影响。

2 编码一致性

(5)

(6)

3 多比特量化

根据前面的分析，当获取了2q个区间后，则利用多个比特编码每个区间内的投影值将变得简单。如q=2时，则有4个区域{sec0,sec1,sec2,sec3}，对应的编码方案为用区域下表索引的二进制形式来表示多比特编码，即4个区域内数据的2 bit编码为{00,01,10,11}。于是获取最优的量化阈值就成为了关键，本文通过线性组合MCC计分项和编码一致性量化误差项E构建量化阈值优化目标函数

Fobj=α·MCC+(1-α)·(1-E)

(7)

式中参数α用来平衡MCC和E，通过最大化式(7)，可以获得一组最优的量化阈值T*

(8)

式中T为候选的一组量化阈值。为了获得T*，本文将选用遗传算法优化目标函数，该算法通过迭代能够逐渐逼近最优解。

遗传算法的初始设置：假设每个投影维需要2q-1个阈值，编码每个阈值的精度为64 bit(preci)，于是级联被这些阈值编码便形成一条染色体。通过实验我们报告了相关参数的设置，包括初始种群(染色体数)为Npop=15，变异概率为Pmut=0.001，交叉概率为Pcro=0.7，新染色体比例为Pggap=0.9，最大繁殖代Nmaxg=20。基于遗传算法优化量化阈值:

输入：相似关系矩阵S，投影值Y，α，q，NpopPmut，Nmaxg，Pggap，Pcro；

输出：量化阈值T*。

初始化：随机产生初始种群Chrom∈{0,1}Npop×(2q-1)×Preci，Chrom中每一行代表一组候选量化阈值

Whilen←1 toNmaxgdo

1)解码Chrom为Npop组候选量化阈值{T1,T2,…,TNpop}，并根据式(7)计算初始种群中所有个体的适应度；

2)排序这些适应度，从Chrom中选取适应度高的[Npop×Pggap]个体进行繁殖，记为Chrom′；

3)基于Pcro，对Chrom′中[Npop×Pggap]/2对染色体进行交叉操作；

4)基于Pmut，对交叉后Chrom′中染色体进行突变操作；

5)利用精英选择方法，合并Chrom′进入Chrom；

end

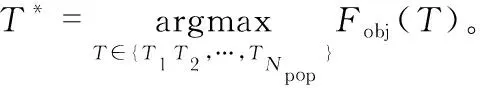
4 实验与结果分析

4.1 数据集与实验设置

本文在典型的图像数据集MNIST上对多比特量化哈希算法进行了评估。对于MNIST数据集，随机抽取1 000个样本作为测试集，1 000个样本作为训练集，余下的作为数据库样本，每组实验进行10次，其结果取平均值。在本文中，采用欧氏距离定义原始特征空间样本的相似关系，计算每个样本的第50个近邻点，对其欧氏距离取平均，小于等于平均距离的将被视为近邻点(相似的)，否则视为非近邻点(非相似的)。另外本文采用典型度量指标对不同的多比特量化进行评估，包括精确度(precision，P)、召回率(recall，R)和P-R曲线面积(auprc)，即以召回率为自变量，以精确度为因变量构成的曲线与坐标围成的面积，即

(9)

4.2 投影方法与量化方法

本文工作主要专注于哈希方法中量化编码阶段，因此投影方法将采用典型的LSH[2]，PCAH[4]，SH[3]和ITQ[5]方法；为了比较本文方法与其他多比特量化方法，选取了传统的SBQ方法以及近年来提出的具有代表性的多比特量化方法——DBQ[7]，MH[8]和NPQ[9]方法，其中SBQ，DBQ，MH为无监督量化方法，而NPQ为有监督量化方法。通过投影方法与量化方法的不同组合，可以得到具体的哈希方法，如“PCAH+Ours”表示一个哈希方法，其投影维由PCAH方法产生，而量化工作则被本文方法完成；需要注意的是，“PCAH+SBQ”等价于原始的PCAH哈希方法，对其他投影方法，类似。根据文献[8]，设定所有量化方法均采用2 bit量化编码每个投影维。

4.3 结果与分析

本文对参数α进行了分析，图1显示了在不同投影方法和不同码字规模下，指标Auprc随着α的变化情况，其中投影方法选取的是LSH和ITQ方法。从图中可知，当码字长度较短(≤96 bit)时，在α∈[0.2 0.5]情况下Auprc值能够达到最大的值；当码字长度较大时(≥96 bit),则α∈[0 0.2]能产生最好的效果。

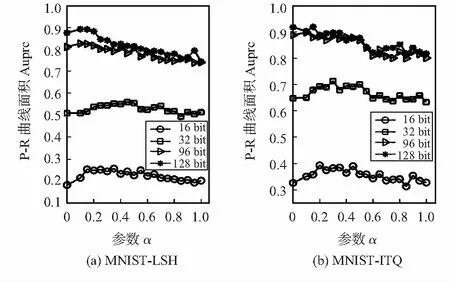
图1 参数α对Auprc的影响

表1给出了编码长度为32 bit和128 bit时的检索表现。表中每个值表示一个具体的哈希方法(即投影方法+量化方法)在特定码字规模下的Auprc值，其最好的结果用粗体标记。从表1中可以观察，相对于数据独立的量化方法(SBQ)，数据依赖的量化方法(DBQ，MH，NPQ和本文方法)能显著哈希检索的效果，同时这些方法用到的投影维数只有SBQ方法的1/2，些发现表明多比特量化方法可以显著减少对投影维的需求，也验证了量化编码的研究对哈希检索具有巨大的促进作用。此外，对比无监督方法(DBQ和MH)，有监督的量化策略(NPQ和Ours)对检索表现达到了约10 %的促进作用。最后，对比所有方法，本文方法的效果均超过了其他流行的量化方法。

表1 MNIST数据集上的量化方法比较

基于4种不同的投影方法，图2提供了不同多比特量化策略在MNIST数据集上的P-R曲线，无论是在短编码(32 bit)下还是在长编码(128 bit)下，本文方法都产生了最好的结果，分析原因是本文提出的多比特量化方法，充分利用了原始数据的相似度信息及局部结构信息，并在编码一致性的约束下，使得原始数据的近邻结构在哈希码空间得到有效保持。这一结果表明了，相对于其他量化方法，利用原始数据的信息来指导量化编码更加有效。

图2 MNIST数据集的P-R曲线

综上所述，本文提出的多比特量化方法对于提高哈希检索的表现是可行的、有效的。

5 结 论

为了在哈希码空间更有效地维持原始数据的相似关系，本文提出了一种新的多比特量化方法，该方法通过结合原始数据的近邻关系及局部信息和数据编码前后的一致性，构建了新的目标函数，在遗传算法的优化下，一组最优的量化阈值被获取，从而实现了投影维的多比特量化及编码。广泛的实验结果显示本文方法相对于其他多比特量化方法，能够提供更好的检索表现。