基于粒子群优化的认知无线电功率分配算法

王宏志, 姜方达, 周明月

(长春工业大学 计算机科学与工程学院, 长春 130012)

随着无线通信技术的快速发展, 人们对无线服务的需求量日益增加, 对服务性能的要求也不断提高, 使得无线电频谱资源变得日益紧缺. 认知无线电[1]能不断感知周围的通信环境, 利用智能技术学习并分析环境信息, 通过无线电知识表达语言实时改变内部通信参数以适应环境的变化, 从而实现任何地点、 任何时间的高可靠传输及对频谱资源的高效利用. 目前, 对频谱检测、 分配、 切换方面的研究主要包括博弈论、 图论着色、 进化算法等. 随着群智能算法的发展, 粒子群优化算法(PSO)、 鱼群算法、 蚁群算法等得到广泛应用. 文献[2-4]将PSO用于解决最大化认知无线电系统的吞吐量问题, 提高了吞吐量, 但系统的公平性较差； 文献[5-6]应用二进制粒子群优化算法优化系统效益, 获得了预期结果； 文献[7-8]应用离散粒子群优化(discrete particle swarm optimization, DPSO)算法和随机漂移粒子群优化(random drift particle swarm optimization, RDPSO)算法, 结合图着色理论优化认知无线网络(CRN)的公平性和实用性, 公平性得到明显提高, 但耗时较大.

用二进制粒子群优化算法优化系统效益, 整体效益虽然提高了, 但收敛速度降低了, 易陷入局部最优. 将DPSO算法与改进DPSO算法用于无线通信中的功率分配, 可提高收敛速度和搜索能力, 但参数权重设置对搜索效率和算法收敛性都有较大影响. 基于此, 本文提出一种新的粒子群优化算法, 在计算出适应度值后加入筛选过程, 并通过引入蒸发因子修改粒子群的记忆形式. 在满足主用户(PU)的干扰功率阈值、 次用户(SU)传输速率和次用户的信干噪比(SINR)需求的前提下, 实现认知系统次用户发射功率的最小化.

1 系统模型

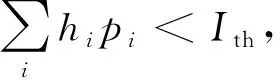
(1)

其中：hij表示SU-Txj与SU-Rxi之间的通道增益；pj表示SU-Txj的发射功率；Ip=p0gi, 表示由PU-Tx到SU-Txi引起的干扰,p0为PU-Tx的发射功率,gi为PU-Tx与SU-Rxi之间的信道增益；N0表示信道上的背景噪声, 假设噪声是独立随机变量CN(0,N0). 次用户的传输速率表示为Ri=log2(1+γi), 其中：Ri表示次用户的传输速率;γi表示次用户的SINR. 在提高通信质量的同时加快传输速率, 以实现更快、 更精准的信息传输, 即Ri≥Rmin, 其中：Ri表示次用户的传输速率；Rmin表示最低传输速率.

在满足主用户的干扰功率门限、 次用户的总传输速率上限以及次用户的SINR要求前提下, 使认知系统的次用户发射功率最小化. 目标函数及约束条件如下：

(2)

当PSO用于求解约束优化问题时, 需根据约束条件设置相应的惩罚函数[9]. 约束优化问题：

(3)

假设x*∈X={x∈n|hi(x)≤0,i=1,2,…,p},hi(x*)≤0,i=1,2,…,p.

定义上述优化问题的惩罚函数为F(x,M)=g(x)+Φp(x), 其中：Φ是大于零的惩罚因子；p(x)是惩罚项. 上述约束定义如下：

(4)

(5)

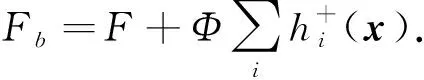
2 功率分配算法

PSO算法源于对鸟类捕食行为的研究. 在PSO算法中, 每个优化问题的解都是搜索空间中的一只鸟, 称为粒子. 在算法运行过程中, 粒子不断使用自己的当前位置和自己的历史最优位置(个体最优值)与种群历史最优位置(群体最优值)进行比较, 然后将结果作为调整其速度和位置的依据[10]. 将种群中每个粒子的状态代入适应度函数, 进行多次迭代最终可使粒子达到最佳位置, 即得到优化问题的最优解. 假设在D维搜索空间中有一个含有n个粒子的种群X={X1,X2,…,Xn},D维搜索空间中每个粒子的位置用D维向量表示. 根据目标函数可计算出每个粒子相对应的适应度值. 同时, 每个粒子也代表一个潜在的问题解决方案. 每个粒子的速度和位置可表示为Vi=(Vi1,Vi2,…,ViD)T和Xi=(Xi1,Xi2,…,XiD)T, 个体最优位置和群体最优位置可表示为Qi=(Qi1,Qi2,…,QiD)T和Qg=(Qg1,Qg2,…,QgD)T. 在每次迭代过程中, 粒子通过个体最优值和群体最优值更新自身的速度和位置, 即

其中：ω为惯性权重；d=1,2,…,D；i=1,2,…,n；k表示当前迭代次数；Vid表示粒子的速度；c1和c2是非负常数, 称为学习因子；r1和r2是分布于[0,1]内的随机数. 为防止粒子的盲目搜索, 一般建议将其位置和速度限制在一定的区间[-Xmax,Xmax],[-Vmax,Vmax]内.

参考文献[11-14], 基于PSO的认知无线电系统的功率分配算法步骤如下：

2) 根据适应度值的计算公式求得个体最优值Qi=(Qi1,Qi2,…,QiD)T和全局最优值Qg=(Qg1,Qg2,…,QgD)T, 其中D表示认知用户的数量；

3) 根据式(6),(7)更新粒子的位置和速度；

4) 更新个体最优值和全局最优值；

5) 当运行到预先设定的最大迭代次数tmax时, 算法结束, 导出当前时刻粒子种群的全局最优值和适应度值; 如果未达到最大迭代次数, 则返回步骤2).

粒子群优化算法是一种随机概率搜索算法, 具有记忆性, 粒子种群的最佳位置可被记忆并传递给其他粒子； 调整参数少, 结构简单易于实现. 但PSO算法缺乏速度动态调整, 有易陷入局部最优、 收敛精度不高、 后期收敛速度慢等缺点. 针对上述缺点, 本文对该算法进行改进. 在PSO算法的初始化阶段会产生大量的随机粒子, 由于粒子随机分布, 一些粒子在计算相应的适应值时会有较大偏差, 从而导致收敛速度下降. 本文采用基于适应度值比例的选择策略对适应度值进行筛选, 个体适应度值越小, 被选中的概率越大. 基于适应度值比例选择策略计算公式为

(8)

其中：εi为个体被选中的概率；Fbi为个体i的适应度值.

筛选完成后, 本文引入蒸发系数对粒子群记忆更新过程进行改进. 基本粒子群记忆的更新形式为

(9)

引入蒸发系数, 使粒子逐渐遗忘自身的记忆, 以适应动态环境. 改进后的粒子记忆更新形式为

(10)

其中ρ为蒸发系数, 由粒子群个体、 社会学习能力(c1和c2)根据Ebbinghaus记忆遗忘曲线[15]加权求得, 计算公式为ρ=0.56[(αc1+βc2)/(c1+c2)]0.06, 其中α和β是分布于[0,1]区间的随机数. 本文改进算法流程如图1所示.

图1 改进算法流程Fig.1 Flow chart of improved algorithm

3 仿真结果与分析

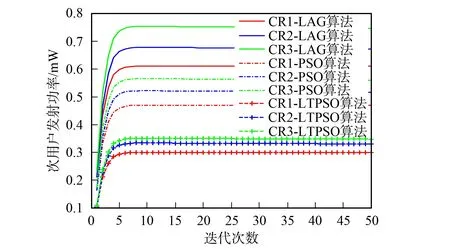
图2 次用户发射功率与迭代次数的关系Fig.2 Relationship between secondary users’ transmission power and iterations

图3 次用户SINR与迭代次数的关系Fig.3 Relationship between secondary users’ SINR and iterations

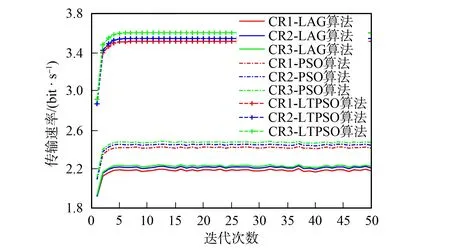
图4 次用户传输速率与迭代次数的关系Fig.4 Relationship between secondary users’ transmission rate and iterations

下面对改进算法进行仿真实验, 选择Lagrange乘子(LAG)算法、 PSO算法和蒸发因子粒子群优化(LTPSO)算法进行对比实验. 所有的仿真实验均在Windows 7系统下通过MATLAB 2014a软件实现, 参数设置： 次用户数量为3, 主用户数量为1, 主用户能承受的干扰功率阈值Ith=1.5 mW, 次用户的SINR需求为5.5～6.5 dB, 次用户的Capacity需求为2.0～2.5, 粒子群大小为100, 粒子群维度为3, 迭代次数为50.

图2为不同算法下次用户发射功率与迭代次数的关系曲线. 由图2可见： PSO算法比LAG算法获得的发射功率更小, PSO算法优于传统的LAG算法; 改进的粒子群优化算法得到的功率明显小于其他两种算法, 在保证各系统都正常通信的情形下, 更好地实现了发射功率最小化的目标.

图3为不同算法下次用户SINR与迭代次数的关系曲线. 由图3可见： 次用户的SINR需求为5.5～6.5 dB, 当SINR=5.5 dB时, LAG算法下次用户不能满足自身需求； 当SINR>6.0 dB时, 只有LTPSO算法才能稳定通信, PSO算法与LAG算法均未达到所要求的SINR； 改进的粒子群算法不仅得到了更小的发射功率, 同时达到了所要求的SINR. 图4为不同算法下次用户传输速率与迭代次数的关系曲线. 由图4可见, 改进的粒子群优化算法得到的传输速率明显高于其他两种算法, 在保证通信可靠性的同时, 也使实时性维持在一个较高的水平.

综上所述, 本文对粒子群优化算法进行改进, 得到了优化后的粒子群算法. 实验结果表明, 改进后的算法所消耗的功率最小, 信噪比也达到了规定值, 提高了通信的可靠性, 同时优化所得的系统容量也是最大的. 相对于PSO算法和LAG算法, 改进后的粒子群优化算法性能最优.