β-Laguerre随机矩阵最大特征值精确渐近性的一般结果

高云峰, 谭希丽

(1. 吉林农业科技学院 文理学院, 吉林 吉林 132101; 2. 北华大学 数学与统计学院, 吉林 吉林 132013)

1 引言与主要结果

随机矩阵特征值在格子气理论与统计力学等领域应用广泛.β-Laguerre总体[1]是随机矩阵特征值的研究热点之一, 其联合密度函数为

其中:λi>0;β>0;m+1>n;Zn,β为正则化常数. 其最大特征值记为λmax(Lβ),Lβ表示β-Laguerre总体下的随机矩阵. 关于随机矩阵特征值的研究最早主要集中在β=1,2,4的特殊情形下, 其最大特征值收敛到经典的Tracy-Wisdom分布. 之后, 文献[1-7]得到了任意β>0情形下的结果, 此时最大特征值的极限分布为广义βTracy-Wisdom(简称为TWβ)分布. 由于TWβ的分布函数和密度函数不能用简单的初等函数表示, 因此, 文献[7]通过随机变分原理给出了TWβ的定义：

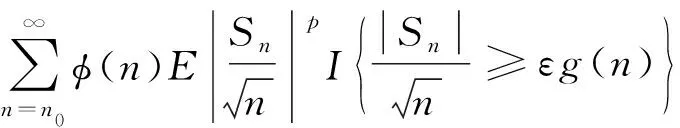
假设条件:

(H1)g(x)为[n0,∞)上具有非负导数g′(x)的正值可导函数, 且g(x)↑∞,x→∞;

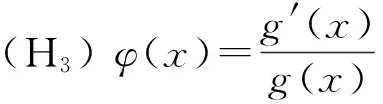
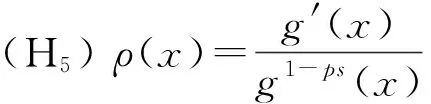
本文主要结果如下:

定理1假设m+1>n,m/n→γ≥1. 如果假设条件(H1),(H2)成立, 则对于s>0,β≥1, 有

(1)

如果假设条件(H1),(H2),(H4)成立, 则对于s-1>p≥0,β≥1, 有

(2)

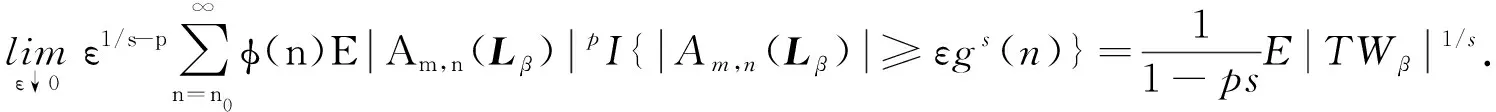
(3)

其中：TWβ为服从广义βTracy-Wisdom分布的随机变量;

定理2假设m+1>n,m/n→γ≥1, 如果假设条件(H1),(H3),(H5)成立, 则对于p≥0,β≥1, 有

(4)

注1满足假设条件(H1)～(H5)的g(x)有很多, 如g(x)=xα, (logx)β, (loglogx)γ等, 其中α>0,β>0,γ>0为适当的参数.

注2广义βTracy-Wisdom分布的任意阶矩存在.

2 定理的证明

引理1[7]假设m+1>n,m/n→γ≥1, 则对于任意的β>0, 有

令Fβ(·)为TWβ的分布函数, 则对于充分大的a, 有

引理2[6]对任意的c1n≤m≤c2n,c2≥c1≥1, 0<ε≤1,β≥1, 有

令a(ε)=[g-1(Mε-1/s)], 其中g-1(x)为g(x)的反函数,M≥1.

类似文献[14]中命题5.1的证明可得:

命题1在定理1的假设条件下, 如果假设条件(H1),(H2)成立, 则有

如果假设条件(H1),(H2),(H4)成立, 则有

命题2在定理1的假设条件下, 如果假设条件(H1),(H2)成立, 则有

证明: 令

(5)

由引理1可知, 当n→∞时,Δn→0. 又由g′(x)的单调性及Toeplitz引理[15]可知, 结论成立.

命题3在定理1的假设条件下, 如果假设条件(H1),(H2),(H4)成立, 则对于p>0, 有

(6)

证明: 显然, 有

其中:

Δn定义如式(5). 根据引理1, 当n→∞时,Δn→0. 首先估计Δn1. 由于n≤a(ε)即εgs(n)≤Ms, 从而有

其次估计Δn3. 由引理1, 可知

最后估计Δn2. 由引理2, 注意到p>0和εgs(n)≤Ms, 有

因此由式(8)～(10), 可得

Δn1+Δn2+Δn3→0,n→∞.

(11)

于是由式(7)、φ(x)的单调性及Toeplitz引理[15], 可知式(6)成立. 证毕.

命题4在定理1的条件下, 如果假设条件(H1),(H2),(H4)成立, 则对于p>0, 有

证明: 注意到s-1>p>0, 由引理1和引理2有

类似命题4的证明可得：

命题5在定理1的条件下, 如果假设条件(H1),(H2)成立, 则有

2.1 定理1的证明

由命题1、 命题2和命题5可知式(1)成立， 由命题1、 命题3和命题4可知式(2)成立. 当s-1>p>0时, 由于

故要证明式(3)成立, 只需证明式(1)及

(12)

成立即可, 从而定理1得证.

2.2 定理2的证明

定理2的证明与定理1的证明类似, 故略.