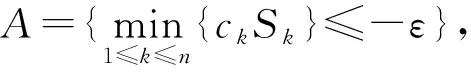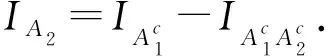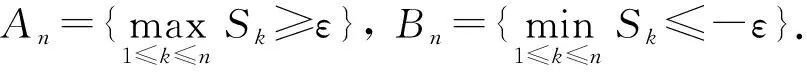弱(下)鞅的最小值不等式

高玉峰, 冯德成

(西北师范大学 数学与统计学院, 兰州 730070)

1 引言与预备知识

设本文的随机变量均定义在概率空间(Ω,A,P)上. 记x+=max{x,0},IA表示集合A的示性函数.

定义1[1]设X1,X2,…,Xn,…是一列L1随机变量, 如果满足

Cov(f(X1,…,Xn),g(X1,…,Xn))≥0,

其中f和g是n上任意两个分量不减的函数且使得上述协方差有意义, 则称随机变量{Xi,i≥1}是相协的(positively associated, PA).

定义2[2]设{Sn,n≥1}是一列L1随机变量, 如果对任意的j≥1, 有

E{(Sj+1-Sj)f(S1,…,Sj)}≥0,

其中f是任意分量不减的函数且使期望有意义, 则称{Sn,n≥1}是一个弱鞅. 进而, 若f是非负函数, 则称{Sn,n≥1}是一个弱下鞅.

由相协随机变量的定义知, 均值为零的相协随机变量序列的部分和是一个弱鞅. 研究表明, 具有自然σ-域的鞅是弱鞅, 具有自然σ-域的下鞅是弱下鞅. 所以, 弱鞅和弱下鞅是较鞅和下鞅更广泛的序列. Wood[3]给出了弱鞅的很多经典性质; Christofides[4]构造了PA序列的U-统计量, 并将其推广到弱鞅序列; Hu等[5]研究了弱鞅的Marshall型不等式; Wang等[6]在凹Young函数的基础上, 建立了关于弱鞅的一些最大值不等式; Dai等[7]建立了弱鞅的最大值不等式; 张丹丹等[8]和冯德成等[9]分别建立了不同的弱鞅最小值不等式. 受上述结果启发, 本文利用弱鞅的性质, 结合凸函数及示性函数, 给出一类弱鞅的最小值不等式.

引理1[10]设{Sn,n≥1}是一个弱鞅或弱下鞅, 如果f是一个非降凸函数, 则{f(Sn),n≥1}是一个弱下鞅.

引理2[10]设{Sn,n≥1}是弱鞅,S0=0, 则对任意的ε>0, 有

2 主要结果

设g是上的一个凸函数,g的左导数定义如下:

因此,h是一个不减的函数, 且有g(y)-g(x)≥(y-x)h(x).

定理1设{Sn,n≥1}是非负弱(下)鞅,S0=0,g(·)是上的一个不减凸函数, 且满足g(0)=0, {cn,n≥1}是一负的、 不增的实数列, 则对任意的ε>0, 有

A1={c1g(S1)≤-ε},Aj={cig(Si)>-ε, 1≤i

当i≠j时,Ai∩Aj=Ø, 且IA2=IA1∪A2-IA1. 由于{cn,n≥1}不增, 因此有

注意到

E[(g(S2)-g(S1))IA1]≥E[(S2-S1)h(S1)IA1],

因为h(S1)IA1是关于S1的非负不减函数, 因此由弱(下)鞅的定义可知,

E[(S2-S1)h(S1)IA1]≥0,

从而

E[(g(S2)-g(S1))IA1]≥0.

又因为{cn,n≥1}是负值, 因此有

c2E[(g(S2)-g(S1))IA1]≤0.

于是可得

注意到

E[(g(S3)-g(S2))IA1∪A2]≥E[(S3-S2)h(S2)IA1∪A2],

因为

A1∪A2={min{c1g(S1),c2g(S2)}≤-ε},

h(S2)IA1∪A2是非负的, 且关于{S1,S2} 的每个分量均不减的函数, 因此, 有

E[(S3-S2)h(S2)IA1∪A2]≥0,

从而

E[g(S3)-g(S2)IA1∪A2]≥0.

(3)

由式(2)和式(3)及{cn,n≥1}是负值, 有

重复上述步骤, 可得

因为

E[(g(Sn)-g(Sn-1))IA1∪A2∪…∪An-1]≥E[(Sn-Sn-1)h(Sn-1)IA1∪A2∪…∪An-1],

且

A1∪A2∪…∪An-1={min{c1g(S1),c2g(S2),…,cn-1g(Sn-1)}≤-ε},

所以h(Sn-1)IA1∪A2∪…∪An-1是非负的, 且关于{S1,S2,…,Sn-1}的每个分量均不减的函数. 又因为{Sn,n≥1}是非负弱(下)鞅, {cn,n≥1}是一负的、 不增的随机变量序列, 故

cnE[(Sn-Sn-1)h(Sn-1)IA1∪A2∪…∪An-1]≤0.

(5)

结合式(4)和式(5), 可得εP(A)≤-cnE(g(Sn)IA). 证毕.

在定理1中, 令g(x)=x可得:

推论2设{Sn,n≥1}是非负弱(下)鞅,S0=0, {cn,n≥1}是一负的、 不增的实数列, 则对任意的ε>0, 有

在定理1中, 若取g(x)=x+, 则g(x)是一个非负的凸函数, 从而可得:

推论3设{Sn,n≥1}是非负弱(下)鞅,S0=0, 且{cn,n≥1}是一负的、 不增的实数列, 则对任意的ε>0, 有

定理2设{Sn,n≥1}是非负弱鞅,S0=0, {cn,n≥1}是一负的、 不减的实数列, 则对任意的ε>0, 有

A1={c1S1≤-ε},Aj={ciSi>-ε, 1≤i

因为IA1是关于S1的非负不减函数, 由弱鞅的定义可知,E[(S2-S1)IA1]≥0, 注意到{cn,n≥1}是负值, 则有c2E[(S2-S1)IA1]≤0. 又由弱鞅的定义可知,ES1=ESn(n≥1). 所以, 可得

因为A1∪A2={min{c1S1,c2S2}≤-ε},IA1∪A2是非负的, 且关于{S1,S2}的每个分量均不减的函数, 因此, 有E[(S3-S2)IA1∪A2]≥0. 又{cn,n≥1}是负值, 则有c3E[(S3-S2)IA1∪A2]≤0. 从而

重复上述步骤, 可得

εP(A)≤-c1E(S1)+cnE(SnIAc).

证毕.

类似定理1, 可得下列结论.

定理3设{Sn,n≥1}是非正弱鞅,S0=0, {cn,n≥1}是一正的、 不减的实数列, 则对任意的ε>0, 有

在定理3中, 令ck恒为1,k≥1, 可得:

推论4设{Sn,n≥1}是非正弱鞅,S0=0, 则对任意的ε>0, 有

定理4设{Sn,n≥1}是弱鞅,S0=0, 则对任意的ε>0, 有

所以

从而

证毕.