两圈之联、路与圈的联及两路之联的邻点被扩展和可区别全染色

张 辉, 陈祥恩, 王治文

(1. 西北师范大学 数学与统计学院, 兰州 730070; 2. 宁夏大学 数学统计学院, 银川 750021)

1 引言与预备知识

关于图的邻和可区别一般边染色的研究目前已有许多结果： 文献[1]给出了图的邻和可区别一般边染色; 文献[2]给出了邻和可区别一般全染色； 文献[3]得出了若G是不含孤立边的图, 则图G的邻和可区别一般边染色数不超过5； 文献[4-6]提出了NSDTC猜想, 并验证了该猜想对3-正则图, 最大度不超过3的图及不含4-阶完全图子式的图等均成立； 文献[7]在此基础上提出了邻点被扩展和可区别全染色, 研究了路、 圈、 完全图、 树等图的邻点被扩展和可区别全染色, 确定了其邻点被扩展和可区别全色数, 并提出了一个猜想. 基于此, 本文考虑两圈之联、 路与圈的联及两路之联的邻点被扩展和可区别全染色.

图G的一个全k-染色是指k种颜色对图G的全体顶点及边的一个分配. 设c是图G的一个全k-染色, 对任意的x∈V(G), 称

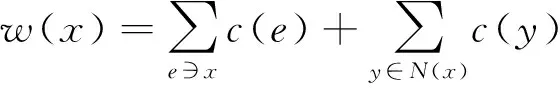
为点x的扩展和, 其中N(x)={y∈V(G)|xy∈E(G)}. 如果w(x)≠w(y), 则称图G的全k-染色c为邻点被扩展和可区别(简记为NESD), 其中xy∈E(G). 图G的NESD全k-染色的最小值k称为图G的邻点被扩展和可区别全色数, 简记为egndi∑(G). 不相交的图G1和G2的联图G1∨G2是指在G1+G2中, 将G1的每个顶点和G2的每个顶点连接起来得到的图[8].

命题1[7]设Pm(m≥2)是m阶的路, 则

命题2[7]设Cm(m≥3)是m阶的圈, 则egndi∑(Cm)=2.

命题3[7]设Kn(n≥2)是n阶的完全图, 则egndi∑(Kn)=2.

命题4[7]设T是n(n≥2)阶的树, 则egndi∑(T)≤2.

猜想1(NESDTC猜想)[7]设G为简单图, 则egndi∑(G)≤2.

2 主要结果

定理1设m≥3,n≥3, 则egndi∑(Cm∨Cn)=2.

证明： 设Cm=x1x2…xmx1,Cn=y1y2…yny1,c是Cm∨Cn的一个全k-染色. 显然Cm∨Cn没有NESD全1-染色, 下面给出Cm∨Cn的一个NESD全2-染色.

情形1)m,n均为偶数且m≠n. 此时, 有

c(x2i-1)=1, 1≤2i-1≤m-1;c(x2i)=2, 2≤2i≤m;

c(y2j-1)=1, 1≤2j-1≤n-1;c(y2j)=2, 2≤2j≤n.

所有的边均染颜色1, 则每个顶点的扩展和计算如下:

显然

w(xi)≠w(xi+1),xixi+1∈E(G);w(yj)≠w(yj+1),yjyj+1∈E(G);

w(x1)≠w(xm);w(y1)≠w(yn).

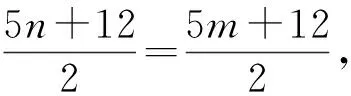
情形2)m,n均为偶数且m=n. 此时, 有

c(x2i-1)=1, 1≤2i-1≤m-1;c(x2i)=2, 2≤2i≤m;c(y2j-1)=1, 1≤2j-1≤n-1;

c(y2j)=2, 2≤2j≤n;c(yjyj+1)=2, 1≤j≤n-1;

除上述3种边染颜色2外, 其余边均染颜色1, 则每个顶点的扩展和计算如下:

显然

w(xi)≠w(xi+1),xixi+1∈E(G);w(x1)≠w(xm);w(yj)≠w(yj+1),

yjyj+1∈E(G);w(y1)≠w(ym);w(xi)≠w(yj), 1≤i≤m, 1≤j≤m.

故当m,n均为偶数且m=n时,c是Cm∨Cn的一个NESD全2-染色.

情形3)m,n均为奇数且m≠n. 此时, 有

c(x2i-1)=1, 1≤2i-1≤m;c(x2i)=2, 2≤2i≤m-1;c(y2j-1)=1, 1≤2j-1≤n;

c(y2j)=2, 2≤2j≤n-1;c(xm-1xm)=2;c(yn-1yn)=2.

除上述两种边染颜色2外, 其余边均染颜色1, 则每个顶点的扩展和计算如下:

显然

(1)

情形4)m,n均为奇数且m=n. 此时, 有下列3种子情形.

① 当m=n=3时,

c(x1)=c(x3)=c(y2)=1,c(x2)=c(y1)=c(y3)=2,

c(x1x3)=c(x1y2)=c(x3y2)=c(x3y3)=c(y1y2)=c(y2y3)=2.

除上述6条边染颜色2外, 其余边均染颜色1, 则每个顶点的扩展和计算如下:

w(x1)=15;w(x2)=12;w(x3)=16;w(y1)=13;w(y2)=17;w(y3)=14.

显然当m,n均为奇数且m=n=3时,c是C3∨C3的一个NESD全2-染色.

② 当m=n=5时,

c(x3)=c(y1)=c(y3)=c(y5)=1.

除上述4个顶点染颜色1外, 其余顶点均染颜色2,

c(x3y1)=c(x4y2)=c(x5y5)=c(y2y3)=c(y3y4)=c(y4y5)=c(y1y5)=2.

除上述7条边染颜色2外, 其余边均染颜色1, 则每个顶点的扩展和计算如下:

w(x1)=18;w(x2)=17;w(x3)=19;w(x4)=18;w(x5)=19;

w(y1)=21;w(y2)=20;w(y3)=22;w(y4)=20;w(y5)=22.

显然当m,n均为奇数且m=n=5时,c是C5∨C5的一个NESD全2-染色.

③ 当m=n≥7时,

c(x1)=c(xm)=2;c(x2i-1)=1, 3≤2i-1≤m-2;c(x2i)=2, 2≤2i≤m-1;

c(y2j-1)=1, 1≤2j-1≤n;c(y2j)=2, 2≤2j≤n-1;

c(x3y1)=c(x4y2)=c(xmyn)=c(y1yn)=2;c(yjyj+1)=2, 2≤j≤n-1.

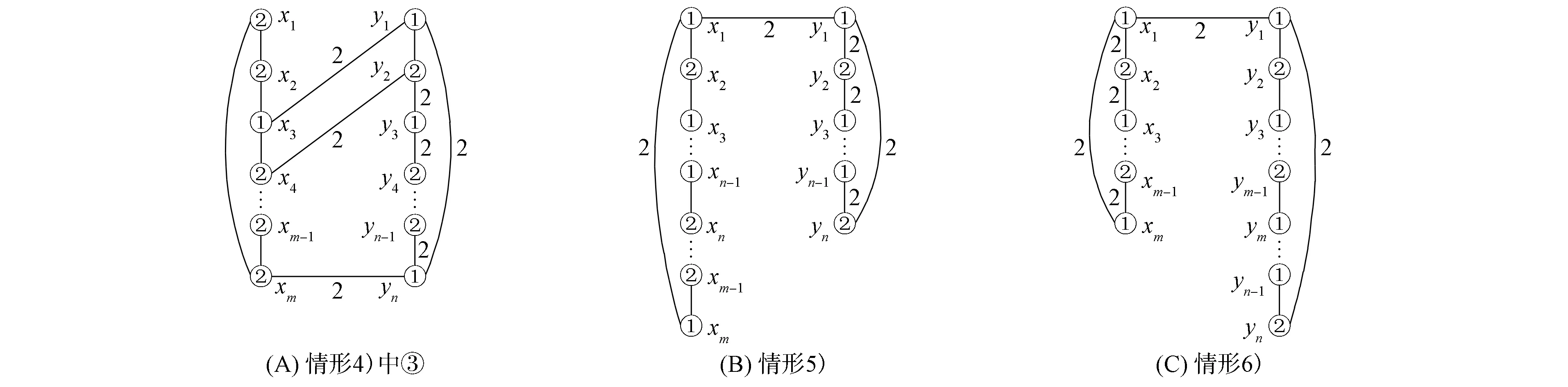
除上述5种边染颜色2外, 其余边均染颜色1, 如图1(A)所示, 则每个顶点的扩展和计算如下:

显然当m,n均为奇数且m=n≥7时,c是Cm∨Cn的一个NESD全2-染色.

情形5)m是奇数、n是偶数且m>n. 此时, 有

c(x2i-1)=1, 1≤2i-1≤m;c(x2i)=2, 2≤2i≤m-1;

c(y2j-1)=1, 1≤2j-1≤n-1;c(y2j)=2, 2≤2j≤n;

c(x1xm)=c(x1y1)=c(y1yn)=2;c(yjyj+1)=2, 1≤j≤n-1.

除上述4种边染颜色2外, 其余边均染颜色1, 如图1(B)所示, 则每个顶点的扩展和计算如下:

显然有式(1).

情形6)m是奇数、n是偶数且m

c(x2i-1)=1, 1≤2i-1≤m;c(x2i)=2, 2≤2i≤m-1;

c(y2j-1)=1, 1≤2j-1≤n-1;c(y2j)=2, 2≤2j≤n;

c(x1xm)=c(x1y1)=c(y1yn)=2;c(xixi+1)=2, 1≤i≤m-1.

除上述4种边染颜色2外, 其余边均染颜色1, 如图1(C)所示, 则每个顶点的扩展和计算如下:

显然有式(1).

图1 不同情形下的NESD全2-染色Fig.1 NESD total 2-coloring under different cases

当m是偶数、n是奇数且m>n时, 由圈与圈联图的对称性可知, 此时与情形6)相同. 同理, 当m是偶数、n是奇数且m

综上可证egndi∑(Cm∨Cn)=2.

定理2设m≥2,n≥3, 则egndi∑(Pm∨Cn)=2.

证明： 设Pm=x1x2…xm,Cn=y1y2…yny1,c是Pm∨Cn的一个全k-染色. 显然Pm∨Cn没有NESD全1-染色, 下面给出Pm∨Cn的一个NESD全2-染色.

情形1)m,n均为偶数且m≠n. 在定理1的情形1)中删去边x1xm后, 即可得Pm∨Cn在m,n均为偶数且m≠n时的一个NESD全2-染色.

情形2)m,n均为偶数且m=n. 在定理1的情形2)中删去边x1xm后, 即可得Pm∨Cn在m,n均为偶数且m=n时的一个NESD全2-染色.

情形3)m,n均为奇数且m≠n. 在定理1的情形3)中删去边x1xm后, 即可得Pm∨Cn在m,n均为奇数且m≠n时的一个NESD全2-染色.

情形4)m,n均为奇数且m=n.

① 当m=n=3时, 在定理1情形4)的①中删去边y1y3后, 即可得P3∨C3的一个NESD全2-染色;

② 当m=n=5时, 在定理1情形4)的②中删去边x1x5后, 即可得P5∨C5的一个NESD全2-染色;

③ 当m=n≥7时, 在定理1情形4)的③中删去边x1xm后, 即可得Pm∨Cn在m,n均为奇数且m=n≥7时的一个NESD全2-染色.

情形5)m是奇数、n是偶数且m>n. 在定理1的情形5)中删去边x1x2后, 即可得Pm∨Cn在m是奇数、n是偶数且m>n时的一个NESD全2-染色.

情形6)m是奇数、n是偶数且m

c(x2i-1)=1, 1≤2i-1≤m;c(x2i)=2, 2≤2i≤m-1;

c(y2j-1)=1, 1≤2j-1≤n-1;c(y2j)=2, 2≤2j≤n;c(xixi+1)=2, 1≤i≤m-1;

c(xtyt)=2, 1≤t≤m;c(yjyj+1)=2, 1≤j≤m;c(y1yn)=2.

除上述4种边染颜色2外, 其余边均染颜色1, 则每个顶点的扩展和计算如下:

显然

w(xi)≠w(xi+1),xixi+1∈E(G);w(yj)≠w(yj+1),yjyj+1∈E(G);w(y1)≠w(yn).

情形7)m是偶数、n是奇数且m>n. 在定理1的情形6)中删去边yn-1yn后, 即可得Pm∨Cn在m是偶数、n是奇数且m>n时的一个NESD全2-染色.

情形8)m是偶数、n是奇数且m

综上可证egndi∑(Pm∨Cn)=2.

定理3设m≥2,n≥2, 则egndi∑(Pm∨Pn)=2.

证明： 设Pm=x1x2…xm,Pn=y1y2…yn,c是Pm∨Pn的一个全k-染色. 显然Pm∨Pn没有NESD全1-染色. 下面给出Pm∨Pn的一个NESD全2-染色.

情形1)m,n均为偶数且m≠n. 在定理1的情形1)中删去边x1xm和边y1yn后, 即可得Pm∨Pn在m,n均为偶数且m≠n时的一个NESD全2-染色.

情形2)m,n均为偶数且m=n. 在定理1的情形2)中删去边x1xm和边y1yn后, 即可得Pm∨Pn在m,n均为偶数且m=n时的一个NESD全2-染色.

情形3)m,n均为奇数且m≠n. 在定理1的情形3)中删去边x1xm和边y1yn后, 即可得Pm∨Pn在m,n均为奇数且m≠n时的一个NESD全2-染色.

情形4)m,n均为奇数且m=n. 此时, 有

c(x2i-1)=1, 1≤2i-1≤m;c(x2i)=2, 2≤2i≤m;c(y2j-1)=1, 1≤2j-1≤n;

c(y2j)=2, 2≤2j≤n;c(yjyj+1)=2, 1≤j≤n-1;c(x2ky2k)=2, 2≤2k≤m.

除上述两种边染颜色2外, 其余边均染颜色1, 则每个顶点的扩展和计算如下:

显然

w(xi)≠w(xi+1),xixi+1∈E(G);w(yj)≠w(yj+1),yjyj+1∈E(G);

w(xi)≠w(yj), 1≤i≤m, 1≤j≤n.

故当m,n均为奇数且m=n时,c是Pm∨Pn的一个NESD全2-染色.

情形5)m是奇数、n是偶数且m>n. 在定理1的情形5)中删去边x1x2和边y1yn后, 即可得Pm∨Pn在m是奇数、n是偶数且m>n时的一个NESD全2-染色.

情形6)m是奇数、n是偶数且m

当m是偶数、n是奇数且m>n时, 由路与路联图的对称性可知, 此时与情形6)相同. 同理, 当m是偶数、n是奇数且m

综上可证egndi∑(Pm∨Pn)=2.

综上所述, 本文首先讨论了两圈之联的邻点被扩展和可区别全染色, 得到了其邻点被扩展和可区别全色数. 然后通过删边的方法得到了路与圈的联及两路之联的邻点被扩展和可区别全染色, 并确定了其邻点被扩展和可区别全色数.