Richardson迭代法的松弛策略

2018-11-28韩光辉渠刚荣

吉林大学学报（理学版） 2018年6期

关键词：迭代法收敛性特征值

韩光辉, 渠刚荣

(北京交通大学理学院, 北京 100044)

图像重建(如电学层析成像、计算机层析成像等)的实验过程可归纳为线性方程组模型

Ax=b,

重建图像的问题即转化为线性方程组的求解问题. 但通常情况下, 因为实验误差导致方程组没有相容性, 很难找到方程组的精确解, 所以采用迭代算法寻找方程组的近似解. Richardson迭代算法[1]即为其中一种, 计算公式如下：

x(n+1)=x(n)+α(b-Ax(n)),

(1)

其中α是松弛参数, 用α取值控制Richardson迭代算法的收敛性和收敛速度. 目前, 关于Richardson迭代算法的研究已有许多结果[2-12]. 文献[4]考虑系数矩阵A为对称正定的情形, 利用Tschebyscheff不等式选取松弛参数α的取值, 该取值方法依赖于矩阵A特征值的下界和上界, 需对矩阵A的所有特征值上、下界进行估计；文献[5]提出了松弛参数取值为α=2/(λlow+λup), 其中λlow,λup分别是对称正定矩阵A所有特征值的下界和上界；文献[6]给出了Richardson迭代法的收敛性证明; 文献[7]针对矩阵A是非对称的情形给出了收敛性证明；文献[8]讨论了复数线性系统下Richardson迭代法的收敛性, 将松弛参数α视为一个取值变化的参数αn, 并给出一种取值方法:

其中ψ(ω)=τω+τ0+τ1ω-1+τ2ω-2+…; 文献[9-10]在对称正定矩阵A的情形下, 对松弛参数的取值给出了更明确的结论：当松弛参数满足0<α<2/λmax时, Richardson迭代法收敛, 且松弛系数的最优取值为2/(λmin+λmax), 这里λmin,λmax分别是对称正定矩阵A的最小和最大特征值. 文献[11]考虑到最小特征值不易计算, 利用矩阵A对角线上最小的元素替代最小特征值λmin, 得到了一个新的常数步长, 并证明了该迭代法的收敛性；文献[12]针对A为对称正定矩阵的情形, 将Richardson迭代法与其他几种基本迭代算法进行对比, 得出结论：随着迭代矩阵谱半径的逐渐变小, 迭代算法的收敛速度越来越快.

本文将Richardson迭代算法推广到求解更一般的线性方程组, 如系数矩阵A是非对称方阵的情形. 利用相似变换矩阵重新表示Richardson迭代算法的迭代过程和迭代矩阵, 根据新的迭代矩阵给出一种最优松弛策略及一种仅依赖于最大特征值的加速收敛策略, 并证明了松弛策略的有效性.

1 预备知识

p1+p2+p3+…+pm=N.

特征值的大小顺序为0<λ1<λ2<…<λm, 对应的线性无关特征向量记作ξk,j(1≤k≤m, 1≤j≤pk), 则有

Aξk,j=λkξk,j.

根据相似对角矩阵的性质, 矩阵A相似于一个对角矩阵[13]. 记Pk=(ξk,1,ξk,2,…,ξk,pk), 则存在非奇异矩阵P=(P1,P2,…,Pm), 使得

P-1AP=Λ=diag(λ1Ip1,λ2Ip2,…,λmIpm),

(2)

这里,Ipk表示pk阶单位矩阵. 矩阵A所有的线性无关特征向量ξk,j可构成空间N的一个基. 若用x+表示方程组(1)的唯一解, 则x+可线性表示为

(3)

且

(4)

其中ck,j∈,k=1,2,…,m,j=1,2,…,pk. 此外, 迭代初始解x(0)可表示为

(5)

定理1对于n=1,2,…, 由Richardson迭代公式(1)得到的迭代解x(n)可表示为

x(n)-x+=(I-αA)n(x(0)-x+)=Pdiag((1-αλ1)nIp1,…,(1-αλm)nIpm)r,

(6)

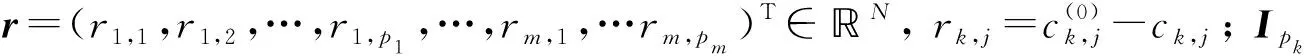
证明: 根据式(1)和式(4), 可得

x(n+1)-x+=x(n)-x++αA(x+-x(n))=(I-αA)(x(n)-x(+)),

(7)

利用递推式(7)可得

x(n)-x+=(I-αA)n(x(0)-x+),

由式(3)和式(5), 可得

x(0)-x+=(P1,P2,…,Pm)r,

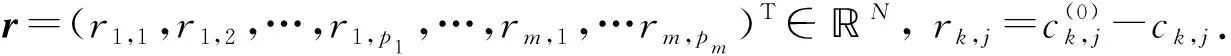
证毕.

令D(α)=diag((1-αλ1)Ip1,…,(1-αλm)Ipm), 则根据定理1可得

[D(α)]n=diag((1-αλ1)nIp1,…,(1-αλm)nIpm),

x(n)-x+=P[D(α)]nr.

根据定理2可得使Richardson迭代法收敛的一个充要条件.

定理3对于由Richardson迭代法得到的逼近序列{x(n)}, 其收敛于方程组唯一解x+的充要条件是: 松弛参数α满足不等式0<α<2/λm.

证明: 为保证收敛性成立, 需要

[D(α)]n→0,n→∞,

根据定理2, 逼近序列{x(n)}收敛于x+的充要条件是ρ(D(α))<1. 由于D(α)是一个对角矩阵, 且其对角元素为(1-αλ1),…,(1-αλm), 所以

当α<0或α≥2/λm时, 因为|1-αλm|≥1, 所以ρ(D(α))≥1. 当0<α<2/λm时, 有|1-αλm|<1. 因为0<λ1<λ2<…<λm, 所以

0<α<2/λm<2/λk, 且|1-αλk|<1,k=1,2,…,m-1.

2 松弛策略

下面给出Richardson迭代法的最优松弛参数和加速收敛策略. 定义迭代误差为

ε(n)∶=x(n)-x+,n≥0.

根据式(6), 定义迭代矩阵为

G(α)=Pdiag((1-αλ1)Ip1,…,(1-αλm)Ipm)P-1,

则有迭代误差表达式

ε(n+1)=G(α)ε(n),n=0,1,2,…

其中ε(0)=Pr. 迭代法收敛的一个充分条件是ρ(G(α))<1, 且谱半径越小, 收敛速度越快. 因此, Richardson迭代算法中的最优松弛策略是指使迭代矩阵的谱半径达到极小值.

定理4对任意一个迭代初始解x(0), Richardson迭代算法的最优松弛参数是

αopt=2/(λ1+λm),

其中λ1,λm分别是系数矩阵A的最小和最大特征值.

证明: 由于0<λ1<λ2<…<λm, 所以对于α>0, 有

1-αλ1>1-αλ2>…>1-αλm,

因此

ρ(G(α))=max{|1-αλ1|,|1-αλm|}.

(8)

又由于

(9)

这里k=1,m. 于是, 根据式(8)和式(9), 可得

(10)

由式(10), 可得

ρ(G(α))=max{1-αλ1,αλm-1},α>0.

(11)

函数ρ(G(α))的极小值点应在直线y=1-αλ1与直线y=αλm-1的交点处取得, 即

1-αλ1=αλm-1.

(12)

由方程(12)解得最优松弛参数αopt. 证毕.

定理5对于任意的α(1)∈(0,1/λm), 其关于点α=1/λm对称点的坐标为α(2)=2/λm-α(1), 即α(2)∈(1/λm,2/λm), 则有ρ(G(α(2)))<ρ(G(α(1))).

证明: 根据式(10)和式(11), 可得

因为1/λm<2/(λ1+λm), 所以

ρ(G(α(1)))=1-α(1)λ1, 0<α(1)<1/λm.

对于α(2)=2/λm-α(1)∈(1/λm,2/λm), 分两种情形讨论：

情形1) 当1/λm<α(2)<2/(λ1+λm)时, 有

ρ(G(α(2)))=1-α(2)λ1<1-α(1)λ1=ρ(G(α(1)))；

情形2) 当2/(λ1+λm)<α(2)<2/λm时, 因为α(2)=2/λm-α(1), 所以有

ρ(G(α(2)))=α(2)λm-1=1-α(1)λm<1-α(1)λ1=ρ(G(α(1))).

综上可知结论成立. 证毕.

3 数值实验

例1求解线性方程组Ax=b, 其中:

x(n+1)=Qx(n)+q,

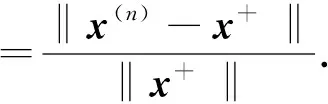
图1为与最优松弛系数对应的迭代误差对比结果, 其中α-和α+分别表示取值比αopt小和比αopt大的α. 由图1可见, 当松弛参数α=αopt时, Richardson的收敛速度较快. 表1列出了当松弛参数取不同数值时对应迭代矩阵的谱半径. 由表1可见, 当松弛参数α=αopt时, 迭代矩阵的谱半径最小.

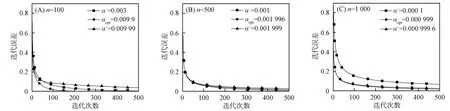
图1 与最优松弛系数对应的迭代误差对比Fig.1 Comparison with iterative error corresponding to optimal relaxation coefficient

表1 对应最优松弛策略的谱半径对比

图2为对应定理5(加速收敛松弛策略)迭代误差的对比结果, 其中αmid=1/λm, 另外两个松弛参数α(1),α(2)的取值是关于αmid=1/λm对称的. 由图2可见, 当松弛参数α=α(2)时, Richardson迭代法的收敛速度较快. 表2列出了在松弛参数分别取α=α(1),α=αmid,α=α(2)时对应的迭代矩阵谱半径. 由表2可见, 对应α=α(2)迭代矩阵的谱半径比对应α=α(1)迭代矩阵的谱半径小.