余纯投射维数换环定理

熊 涛, 王芳贵, 乔 磊

(1. 西华师范大学 数学与信息学院, 四川 南充 637002; 2. 四川师范大学 数学与软件科学学院, 成都 610068)

1 引言与预备知识

设R是给定的环, gl.dim(R)表示R的整体维数, 如无特别说明,R-模均指左模. 设M是R-模, fdRM表示M的左平坦维数. 其他相关符号参见文献[1-2].

若存在分解的正合列投射模P=…→P1→P0→P0→P1→…, 使得M≅Im(P0→P0)和函子HomR(-,Q)对序列P还是正合的, 则称R-模M为Gorenstein投射模(简称G-投射模), 这里Q是投射R-模. 若投射R-模的子模是Gorenstein投射的, 则称环R为Gorenstein遗传环. Gorenstein遗传整环称为Gorenstein Dedekind整环. 文献[5]中定理2.6证明了一个Neother整环R是Gorenstein Dedekind整环当且仅当R是CPH环, 即cpD(R)≤1. 文献[8]中定理3.15证明了整环R是Gorenstein Dedekind整环当且仅当R是CPH整环. 若存在正合列

0→Pn→Pn-1→…→P1→P0→M→0,

则称模M的Gorenstein投射维数不超过n, 记为GpdRM≤n, 这里每个Pi都是Gorenstein投射模.R的Gorenstein整体维数G-gl.dim(R)定义为sup{GpdRM|M是R-模}. 由文献[3]中注记4.2和文献[9]中命题1.3知，R是QF环当且仅当G-gl.dim(R)=0, 当且仅当cpD(R)=0. 更一般地, 文献[8]中命题3.17证明了对一个满足G-gl.dim(R)<∞的Noether环R, G-gl.dim(R)=cpD(R)成立. 因此R的余纯投射整体维数cpD(R)作为一种较新定义的同调维数, 与G-gl.dim(R)联系密切.

经典同调理论中的整体维数和弱整体维数都有相应的换环定理. 文献[10]给出了Gorenstein投射维数的换环定理. 文献[8]证明了R是QF环当且仅当对任意R上的未定元x, 其多项式环R[x]是CPH环; 一个整环R是CPH环当且仅当对R的任何非零因子非单位u,R/(uR)是QF环, 即给出了关于余纯投射维数的换环定理. 但文献[8]并未给出余纯投射维数换环定理的直接表述, 本文给出其直接表述.

2 主要结果

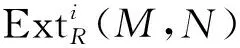
证明: 设N是平坦T-模. 由平坦维数换环定理, 可得fdRN<∞. 因此, 存在内射T-模E及正合列0→N→E→C→0. 从而可得如下行是正合列的交换图:

设0→K0→F0→M→0是正合列, 这里F0是自由R-模. 由假设可得正合列

⊗RK0→T⊗RF0→T⊗RM→0.

注意到T⊗RF0是自由T-模, 则对所有的k≥0, 均可得如下同构：

显然可得下列推论.

推论1设M是强余纯投射R-模， 则M[x]是强余纯投射R[x]-模.

推论2设R是交换环,S是R的一个乘法封闭集. 如果M是强余纯投射R-模, 则MS是强余纯投射RS-模.

为方便, 用S (R)表示位于R中心的既不是零因子也不是单位元素的集合.

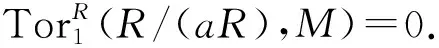
推论3设a∈S (R),M是强余纯投射R-模, 且a不是M的零因子. 则M/(aM)是强余纯投射R/(aR)-模.

证明: 记T=R/(aR), 则fdRT≤1. 由定理1和引理2可得结论.

命题1设M是左R-模, 则cpdR[x](M[x])=cpdR(M).

证明: 设m是一个非负整数. 如果cpdR(M)≤m, 则由文献[3]中命题4.6可知, 存在正合列

0→Pm→Pm-1→…→P1→P0→M→0,

这里每个Pi都是强余纯投射R-模. 从而

0→Pm[x]→Pm-1[x]→…→P1[x]→P0[x]→M[x]→0

也是正合的. 由推论1可得cpdR[x](M[x])≤m.

另一方面, 设cpdR[x](M[x])≤m, 则存在正合列

0→Fm→Fm-1→…→F1→F0→M[x]→0,

这里F0,F1,…,Fm-1是自由R[x]-模, 且Fm是强余纯投射R[x]-模. 由于x是M[x]的非零因子, 可得正合列

0→Fm/(xFm)→Fm-1/(xFm-1)→…→F1/(xF1)→F0/(xF0)→M→0.

由推论3可知, 每个Fi/(xFi)都是强余纯投射R-模. 故cpdR(M)≤m, 从而cpdR[x](M[x])=cpdR(M)成立.

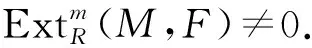
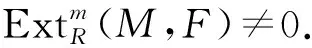
定理2设a∈S (R), 记T=R/(aR). 则: 1) 设M是非零左T-模, 且cpdT(M)=m<∞, 则cpdR(M)=m+1; 2) 若cpD(T)<∞, 则cpD(R)≥cpD(T)+1.

2) 记m=cpD(T), 则存在T-模M, 满足cpdT(M)=m. 由1)有 cpdR(M)=m+1. 因此cpD(R)≥m+1.

对交换环R, 可得下列推论.

推论4设a∈S (R), 记T=R/(aR). 如果gl.dim(R)≤m, 则cpD(T)≤m-1. 特别地, 如果R是遗传环, 则T是QF环.

推论5设R是整环,a∈R非零非单位, 记T=R/(a). 如果cpD(R)≤2, 则T是CPH环.

推论6设R是整环,a∈R非零非单位, 记T=R/(a). 如果gl.dim(R)≤2, 则T是CPH环.

推论7设R是伞环且满足gl.dim(R)≤2. 对任意的0≠a∈P, 这里P是R的非有限生成极大理想, 记T=R/(a). 则T是凝聚非Noether的CPH环.

一般地, 对于环R的真理想I, cpD(R)≥cpD(R/I)+1未必成立. 下面举例说明.

例1构造环R=+x2[x], 这里是有理数域,x是上的一个未定元. 则由文献[12]中例4.1可知,R是Gorenstein Dedekind整环. 由文献[8]中定理3.1和定理3.15可知, cpD(R)≤1成立. 下面构造R的真分式环注意到是一个以为唯一极大理想的局部Artin环, 且则不是QF环. 再由文献[3]中注4.2可得,

定理3对任意环R, cpD(R[x])=cpD(R)+1.

证明: 由命题1, 不妨设m∶=cpD(R)<∞. 由定理2, 可得cpD(R[x])≥m+1. 设A是R[x]-模. 考虑经典的R[x]-模正合列 0→A[x]→A[x]→A→0. 由文献[3]中命题4.10(3)及命题1, 有

cpdR[x](A)≤cpdR[x](A[x])+1=cpdR(A)+1≤m+1.

因此cpD(R[x])≤m+1.

定理4设R是交换环,S是R的乘法封闭集. 则cpD(RS)≤cpD(R).

证明: 不失一般性, 假设m∶=cpD(R)<∞. 对任意RS-模M, 存在正合列

0→Pm→Pm-1→…→P1→P0→M→0,

其中每个Pi是强余纯投射R-模. 则可得正合列

0→(Pm)S→(Pm-1)S→…→(P1)S→(P0)S→M→0.

由推论2知, 每个(Pi)S是强余纯投射RS-模. 从而cpD(RS)≤m.

若R是交换的Noether环, 则环R的整体维数有如下性质:

gl.dim(R)=sup{gl.dim(Rm)|m取遍R的全部极大理想}.

对于cpD(R), 有下列推论.

推论8[8]若R是交换的Noether环, 则cpD(R)=sup{cpD(Rm)|m取遍R的全部极大理想}.