适用于海量负荷数据分类的高性能反向传播神经网络算法

刘 洋, 刘 洋, 许立雄

(四川大学电气信息学院, 四川省成都市 610065)

0 引言

负荷分类对电网经济分析和安全可靠运行具有重要意义,并且可对订制电价[1]、负荷预测[2]、系统规划、负荷管理与负荷建模[3]等提供基础和参考。长期以来,负荷分类是智能电网数据挖掘的一个重要方面,如何对电力负荷数据高效准确地分类受到诸多学者的广泛关注和研究[3-6]。

近年来,利用人工智能神经网络算法进行负荷分类和预测,取得了良好实际效果,其根据训练样本不断迭代更新网络参数,具有良好的学习和容错能力,且不受负荷成分和特性限制,具有描述复杂动态行为方面的优势。其中,反向传播神经网络(back propagation neural network,BPNN)算法作为神经网络训练采用最多、也是最成熟的分类算法之一,具有极强的函数逼近与模式分类能力,在负荷模型辨识中应用广泛。文献[5]提出了一种基于模糊聚类与改进的反向传播(BP)算法的负荷特性曲线分类方法,在C-均值聚类得到典型负荷曲线后,结合多种环境因素作为学习样本建立BP模型,取得良好的分类效果。文献[6]利用模糊理论对典型BPNN算法进行参数修正,提出自适应神经网络有效提高负荷建模的速度和精度。文献[7]建立基于知识挖掘分类技术的自适应结构日负荷曲线BPNN算法预测模型,通过计算负荷曲线相似度对历史数据进行排序与初步分类,再利用BPNN算法对误差纠偏得到的负荷分类模型进行更加精确的负荷预测。

然而,随着智能电表的普及与传感器技术、通信技术的发展,负荷数据采集间隔缩短,数据量成倍增加,用户负荷数据呈现出体量大、类型多、速度快、随机性强等特点[7-9]。面向海量负荷数据,采用神经网络分类往往由于学习过程中训练样本过大导致效率低下。而并行计算可将任务划分,是应对海量数据计算速度缓慢的一种有效方式。文献[8]提出一种基于分布式计算框架Hadoop的电力用户侧大数据管理方案,利用并行化框架对负荷数据挖掘,有效提高数据处理效率。文献[10]提出一种基于Hadoop架构的多重分布式短期负荷预测方法,在多重概念的基础上综合考虑灰色关联度、最短距离聚类法和有效指标方式,在达到传统BP模型预测效果且弱化“过拟合”问题的同时,大大降低预测过程的耗时。与Hadoop框架相比,Spark平台是一种更加高效的分布式计算平台,不仅可应用Hadoop框架下的分布式文件系统(Hadoop distributed file system,HDFS),具有MapReduce模型的优点,而且采用弹性分布式数据集(resilient distributed dataset,RDD)将集群分布式计算数据缓存在各个节点内存中,避免大量I/O过程,在处理迭代问题时效率优于Hadoop数倍,具有计算更加高效的优点[11-12]。

本文提出一种适用于海量负荷数据分类的高性能BPNN算法。主要工作为:①在Spark平台上将BPNN算法并行化,将训练样本抽样分块以减少各网络训练时间;②采用集成学习以应对分块后训练样本缺失导致BPNN基分类器分类精度下降的问题[13],集成学习过程包括构建差异化基分类器与多数投票获得分类结果;③提出一种基于聚类算法的BPNN训练样本选取方法以适应负荷模型的多样性,反映真实用户负荷类型。

1 集成神经网络负荷分类方法相关理论

本文在大数据处理平台Spark上实现一种差异化BPNN并行集成学习(ensemble BPNN based on Spark,EBPNN)算法用于负荷数据分类。其基本思想是:抽样获得原训练数据集多个子集,通过BPNN并行化实现单独学习各子集形成性能差异的基分类器,最终通过多个基分类器共同决定数据分类结果。图1是集成分布式神经网络分类方法总体框架。

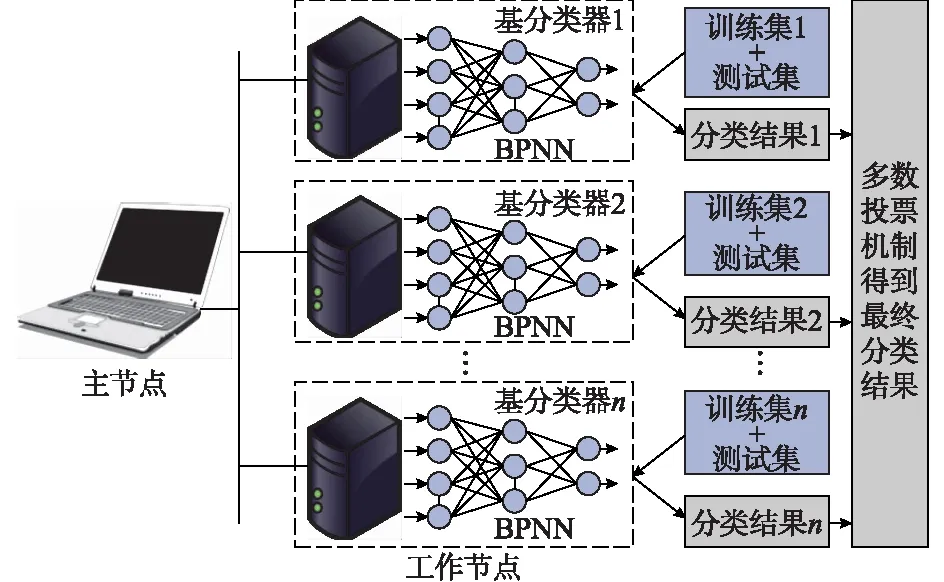
图1 基于Spark平台的EBPNN算法分布式框架Fig.1 Distributed framework of EBPNN algorithm based on Spark platform

1.1 BPNN算法

图1中各基分类器的主体是BPNN,BPNN是一种多层前馈网络,通过输入信号正向传播和误差信号反向传播对网络参数进行调整,具有极强的函数逼近和模式分类能力[14],BPNN由输入层、隐含层、输出层组成。选取log-sigmoid函数作为网络传递函数,即

(1)

设输入任意训练数据为Xr=[x1,x2,…,xm]T,分别得到隐含层向量和输出层向量为Yr=[y1,y2,…,yp]T和Or=[o1,o2,…,ol]T,期望输出向量为Dr=[d1,d2,…,dl]T,其中,m,p,l分别表示输入层、隐含层和输出层的神经元个数;输入层到隐含层的权值和偏置值分别为wij和bij(i=1,2,…,m;j=1,2,…,p),隐含层到输出层的权值和偏置值分别为wjk和bjk(j=1,2,…,p;k=1,2,…,l)。正向传递过程为:

(2)

误差E为输出信号Or与期望输出Dr的距离表示为:

(3)

反向传播过程按照最速下降法更新权值和偏置值,使误差E不断减小,权值和偏置值调整量Δw和Δb以及w和b的调整过程表示为:

(4)

(5)

式中:α为学习速度,α∈(0,1)。

1.2 基分类器训练样本的获取

为构建多个具有差异化特性的基分类器,需要各基分类器的训练样本存在差异。有差异的训练样本可通过对原始数据的抽样产生。本文采用自助法(bootstrapping)[15]、分层抽样 (stratified random sampling,SRS)[16]和拉丁超立方抽样 (Latin hypercube sampling,LHS)[17]。但直接抽样原始数据无法保证训练样本覆盖所有的数据类别,因此采用先对部分数据聚类再选取类中心附近数据的方式以优化训练样本。

K-means算法具有对少量数据聚类收敛速度快、聚类复杂度低及可扩展性好的优点[18]。其聚类结果能体现原始负荷数据大致分类,但是处于各类交界的数据会出现类别模糊现象。而K-medoids算法是从当前类中选取到类内其他所有曲线距离之和最小负荷数据作为类簇中心,能够有效降低极端值的影响[19]。本文采用K-means算法对部分负荷数据聚类,添加数据属性标签,为避免模糊类别负荷曲线对分类效果的影响,通过K-medoids聚类中心确定方法择优选取部分负荷数据作为训练样本。

1.3 最终分类结果获取的多数投票机制

在各基分类器分类结果的基础上采用多数投票机制[20]获得集成学习分类的最终结果,假设某一基分类器Ci的分类结果为Rij;i=1,2,…,I;j=1,2,…,J;其中I和J分别为分类器数和类别数;Rij∈{0,1},当Ci将该数据分类为j类时Rij=1,否则Rij=0。分类结果表示为:

(6)

2 基于集成学习的分布式神经网络分类算法

EBPNN分类算法主要包括负荷数据的预处理、负荷数据训练样本的选取与分块、负荷数据的样本训练和负荷测试数据的分类等步骤。图2是EBPNN算法对海量负荷数据分类的流程示意。

图2 EBPNN算法流程图Fig.2 Flow chart of EBPNN algorithm

2.1 EBPNN算法流程

EBPNN海量负荷数据分类算法的具体步骤可描述如下。

1)负荷数据预处理:删除包含空缺值和记录天数过少(小于10 d)的用户负荷曲线,并按照式(7)进行数据归一化处理,即

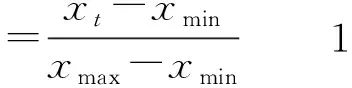
(7)

式中:xt,xt′,xmax,xmin分别为日负荷曲线中t时刻负荷值、归一化后t时刻负荷值、最大负荷值和最小负荷值;T=48为每日时段数。

2)负荷训练样本分块过程,通过抽样原始负荷训练样本X获得n(n=3,5,7,…)个等量负荷训练样本块,其过程表示为:

Xsample={X1,X2,…,Xn}

(8)

式中:X1∪X2∪…∪Xn=X;n为负荷训练样本块数目;将负荷测试样本T加入每个负荷样本块并将文件保存在HDFS中;负荷训练数据格式为〈label,data,target〉,负荷测试数据格式为〈label,data〉,两者通过行首标签〈label〉区分;〈data〉为一负荷曲线特征向量,〈target〉为该负荷训练数据期望输出,即〈data〉所属类别。

3)负荷训练过程,从HDFS上读取包含负荷训练样本块和负荷测试样本的文件,Spark平台启动mapper的个数取决于读取文件的个数,每个mapper包含一个BPNN。首先,为每个BPNN随机初始化权重和偏置值,其后将Xi输入到第i个BPNN,通过“train”标签识别负荷训练数据,负荷样本特征向量维度决定了BPNN输入层神经元个数,正向传播过程根据式(2)计算得到隐含层和输出层结果。反向传播过程按照式(3)至式(5)进行参数更新,直到误差值满足给定条件时训练结束,形成分类性能不同的基分类器Trained Sub-BPNNi;i=1,2,…,n,训练过程见附录A图A1(a)。

4)负荷分类过程,通过“test”标签识别负荷测试数据并输入到所有基分类器,Trained Sub-BPNN基分类器只进行正向传播过程得到某一负荷测试数据分类结果,表示为〈data,Rij〉。通过reduceByKey将该负荷数据所有分类结果收集得到〈data:R1,R2,…,Rn〉,按照式(6)投票获得最终分类结果。负荷数据分类过程见附录A图A1(b)。负荷数据处理过程对应弹性分布式数据集(RDD)的逐步转换,最终分类结果写入HDFS中。

2.2 训练样本选取过程

采用BPNN算法进行负荷数据分类时,负荷训练样本质量直接影响分类效果。随着负荷设备构成的复杂化趋势与新能源接入电网对用户负荷特性的影响,传统负荷类型难以表征实际的负荷变化规律,海量负荷数据分类的训练样本难以获取。提出一种结合K-means和K-medoids算法的负荷训练样本选取方法,立足实际的负荷数据,适应更加多元化的用户用电模式。具体过程如下。

步骤1:初始化类簇中心:在由U个负荷数据对象组成的数据集X={x1,x2,…,xU}中,xu={xu1,xu2,…,xuV},初步确定分类个数K和各类簇中心M={m1,m2,…,mK}，mk={mk1,mk2,…,mkV}。其中,U和V分别表示负荷向量数量和向量维度,u=1,2,…,U;v=1,2,…,V。

步骤2:簇划分,按式(9)计算任意一条负荷曲线与初始类簇中心的欧氏距离,将各曲线分配给距离最近的类簇中心,形成K个类簇,即

(9)

步骤3:更新类簇中心,按式(10)重新计算每个类簇所有负荷曲线均值作为新的类簇中心,即

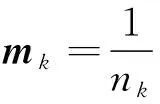
(10)

式中:nk为Ck类的负荷样本个数;Zk为Ck类的负荷样本。

步骤4:重复步骤2和步骤3,直到聚类中心不再发生变化时结束类簇中心更新过程。

步骤5:根据K-medoids算法聚类中心选取方式,按式(11)计算每条负荷曲线与其所属类内其他曲线的距离之和DΣ,在每个类中选取DΣ值最小的η个负荷曲线作为负荷训练样本,即

(11)

式中:Dij为负荷数据i到类内数据j的欧氏距离,DΣi为负荷数据i到类内其他所有数据点的欧氏距离。

3 算例分析

3.1 训练样本合理性验证

训练样本的选取过程见附录A图A2。图A2(a)为原始3种类型的数据点集。图A2(b)为K-means聚类后,以圆圈形式覆盖在原始点集上的聚类结果。可以看出,通过K-means聚类能比较准确地反映原始数据类别。但是在类间交汇处有少量数据点在聚类后与其原始类型不同,为择优选取靠近类别中心的数据,通过K-medoids算法选取如附录A图A2(c)中紫色点集作为训练样本,从而规避了模糊类别训练样本对网络学习的影响。另外,在原始数据中随机选取部分数据作为噪声点以避免“过拟合”问题[21-22]。

3.2 数据来源

EBPNN算法先在两个经典分类数据集上进行精度合理性验证,并对比分析参数变化对精度的影响,再将其应用到实际用户负荷数据分类中。算例数据选取经典分类数据集Iris和Wheat Seeds数据集以及爱尔兰智能电表实测用户用电数据。Iris和Wheat Seeds数据集数据特征如表1所示。

表1 Iris和Wheat Seeds数据集数据特征Table 1 Data characteristics of data set Iris and Wheat Seeds

用户负荷数据选取爱尔兰可持续能源管理局(Sustainable Energy Authority of Ireland,SEAI)于2011年5月发布的爱尔兰智能电表实测用户用电数据[23],负荷数据特征为:用户6 000个,日采集点48个,采集天数536 d,数据量约3.06×106个。本文算例在单台CPU为Core i5 2.50 GHz,内存为16 GB的PC机搭建的3台虚拟机上实现,其中一个作为主节点,包括主节点在内的3个节点作为工作节点,集群配置情况如表2所示,系统采用Ubuntu 16.04.2 LTS,Spark 版本为1.6.2。

表2 计算节点配置Table 2 Configuration of computation node

3.3 Iris与Wheat Seeds数据分类实验及参数分析

3.3.1训练样本与测试样本数据量对分类结果的影响

为研究训练样本与测试样本数据量对分类结果的影响,固定其他参数(EBPNN算法训练样本块个数为3,训练样本块数据量取相应训练样本的1/2),改变训练样本与测试样本数据量,测试得到不同情况下传统串行BPNN与EBPNN分类正确率见附录A图A3。

可以看出,基于分层抽样的分布式BPNN算法具有较高的准确率,并且在样本数量较少时,准确率较单机BPNN算法更高,且较其他并行BPNN算法更稳定。在样本数量逐渐增大的过程中,EBPNN算法的准确度与单机BPNN算法准确度逐渐接近,并未表现出分布式后算法由于分割训练数据所导致分类准确度下降。

3.3.2训练样本块数据量对分类结果的影响

为研究训练样本块数据量对分类结果的影响,固定其他参数(Iris数据集训练样本/测试样本=50/100,Wheat Seeds数据集训练样本/测试样本=60/150,训练样本块个数为3),改变各训练样本块数据量,测试训练样本块数据量改变时采用自助法、SRS和LHS的EBPNN算法分类正确率见附录A图A4。

训练样本块数据量增加过程中,分类正确率先提高,而后基本保持不变。这是因为在该固定参数情况下,Iris和Wheat Seeds数据集训练样本块数据量达到某一体量时已足够使网络学习充分且多基分类器的差异性恰能达到良好的集成学习效果。

3.3.3基分类器个数对分类结果的影响

集成学习过程通过将多个基分类器分类结果进行多数投票获得最终分类结果,为研究基分类器个数对分类正确率的影响,固定其他参数(Iris数据集训练样本/测试样本=50/100,各训练样本块为训练样本数据量的1/2,即训练样本块数据量为25;Wheat Seeds数据集训练样本/测试样本=60/150,各训练样本块为训练样本数据量的1/2,即训练样本块数据量为30),改变训练样本块个数,即基分类器个数,测试各算法分类正确率见附录A图A5。

两数据集在训练样本块为3时,分类精度较低,训练样本块为5,7,9时,分类精度有所提高,但变化不大,仅在Wheat Seeds数据集采用EBPNN(LHS)算法时,分类效果较差,这是因为LHS破坏了原始数据的完整性,改变了原始特征向量,在某些情况下会降低分类正确率。此外,应适当选择训练样本块个数,过少时可能具有偶然性影响分类精度,过多时须考虑系统配置情况。

通过对比Iris和Wheat Seeds数据集的分类效果可知,EBPNN算法分类精度较高且在某些情况下高于传统串行BPNN算法。而SRS法需要根据具体待分类数据特征选择,自助法抽样随着被抽样数据量的增加,所抽数据对原始数据的覆盖率逐渐降低,因此EBPNN (Bootstrapping) 算法更适合较小训练数据体积的数据分类中;LHS法是对输入概率分布进行分层,能够确保偏远事件在模拟的输出中被准确地代表,会破坏原始数据,也因此可能影响所选训练样本块的质量;EBPNN(SRS) 算法相较于其他两种EBPNN算法分类效果和稳定性更好,一方面SRS法能够获得均匀分布的训练样本,另一方面SRS法不会打乱原始样本的整体性与属性间的相关性。两经典数据集分类结果表明,EBPNN算法具有合理性与有效性,且采用SRS法获取训练样本块更有利于提升分类器的分类性能,可应用到电力系统用户负荷大数据的分类中。

3.4 爱尔兰负荷数据分类

3.4.1负荷分类

本节在分布式数据处理平台Spark上对全部爱尔兰智能电表实测用户用电数据(约3.06×106条曲线)进行分类,并与直接进行K-means聚类结果进行对比,与单机模式进行效率对比。

选取第1～236 d负荷曲线为待选训练样本,后300 d数据作为测试样本。训练样本选取过程中,初始聚类数K值采用误差平方和(sum of squared error,SSE)确定,将SSE曲线拐点作为最佳聚类数。

根据图3所示SSE曲线,选择聚类数K=8。神经网络所学习的差异化训练样本通过SRS获得,基分类器个数为5,各训练样本块数据量取总训练样本量约2/3,图4所示为负荷分类结果。

图3 SSE曲线Fig.3 Curve of SSE

图4 负荷分类结果Fig.4 Results of load classification

根据图4(a)对居民用电1 d共48时段用电情况的分类结果可以看出,用户侧用电形式多样,差异性大。其中包括平稳用电负荷和尖峰用电负荷,第1类负荷始终保持较高水平,尤其在凌晨时段用电偏高;第2类负荷水平始终很低;第3类和第7类是典型午间负荷,白天保持较高的用电水平;第4,5,6,8类是典型晚间负荷,白天用电量很少,而到晚间用电量攀升。图4(b)为在各类中随机抽取的部分负荷曲线。可以看出,同类负荷曲线具有相似趋势,平稳负荷曲线与质心区别较大,是归一化后曲线有尖峰数值所致。总数据量约为1 030 MB,EBPNN算法在Spark平台分类用时41.2 s。

3.4.2算法性能评估

1)分类质量评估

聚类后曲线和质心的戴维森堡丁指数(Davies-Bouldin index,DBI)代表任意两类别类内距离平均值之和与两类别质心距离之比的最大值,其值越小意味类内距离越小,类间距离越大;轮廓系数(silhouette coefficient,SI)能有效表示类别内聚度和分离度,值越接近1表明分类效果更佳[24]。设置不同聚类数K(K=2～12)时,对比采用K-means和EBPNN(SRS)算法分类时两指标变化情况如图5所示。可以看出,当K=2,DBI和SI分别达到最小和最大,K=8其次,而类别数为2时,类别过少,分类过于粗略,因此K=8更加合理。另外,对比聚类数K=8时的归一化后数据类内标准差,各类别标准差如图5(c)所示,EBPNN(SRS)算法分类结果较K-means类内标准差更小。

图5 分类质量对比Fig.5 Comparison of classification quality

2)分类效率评估

为对比并行EBPNN算法与传统串行BPNN算法的效率,测试各算法运行时间随数据量变化关系,固定EBPNN算法基分类器个数为5,得到测试结果如图6所示。可以看出,当数据体积小于32 MB时,串行模式的BPNN算法运行时间更短,而数据量超过32 MB时,EBPNN算法效率显著提高。这是由于数据量较小时,系统开销占主导作用,而数据量大时,系统开销对运行时间影响较小,并行计算效率优势明显。

图6 计算效率对比Fig.6 Comparison of computation efficiency

4 结语

本文提出一种基于集成学习的分布式神经网络负荷分类方法,在Spark平台上实现BPNN算法并行化对用户侧大数据分类,为解决海量用户负荷分类问题提供一种新的思路。算法通过K-means聚类少量局部数据以获取类别标签,K-medoids算法对聚类结果进行训练样本选取,能够提取更加切合实际的负荷类型曲线。经典分类数据集和爱尔兰实测用户负荷算例的应用表明所提方法具有高效性和实用性。

该算法能快速提取用户负荷类型并进行负荷分类,有效对居民用电模式深入分析,为配电网安全可靠运行奠定基础,且能够延展到多领域数据分类分析场景。

附录见本刊网络版(http://www.aeps-info.com/aeps/ch/index.aspx)。