动态EEAC的自适应分段映射
2018-11-26黄天罡薛禹胜林振智文福拴
黄天罡, 薛禹胜, 林振智, 文福拴, 徐 岩, 岳 东
(1. 东南大学电气工程学院, 江苏省南京市 210096; 2. 南瑞集团(国网电力科学研究院)有限公司, 江苏省南京市 211106;3. 智能电网保护和运行控制国家重点实验室, 江苏省南京市 211106; 4. 浙江大学电气工程学院, 浙江省杭州市 310027;5. 南洋理工大学电力与电子工程学院, 新加坡 639798; 6. 南京邮电大学先进技术研究院, 江苏省南京市 210023)
0 引言
稳定算例筛除技术通过机器学习技术[1]或近似的因果算法[2],从大量算例中识别并筛除稳定算例,以减少总计算量。但其中若将实际失稳(或稳定)的算例误判为稳定(或失稳),就形成风险性(或降效性)误判。算例筛除方法应该在完全杜绝风险性误判的前提下,尽量减少降效性误判。为此,相关的筛除规则应具有相对严格的因果背景,并与统计分析技术深度融合来减少计算量[3]。
文献[4-5]从数值积分所获受扰轨迹中,提取可反映该算例的非同调程度及非哈密顿程度的指标,预估后续轨迹的稳定性,并决定是否提前终止数值积分。这些指标虽然在一定程度上反映了稳定性的因果关系,但主要还是在统计分析层面上归纳了时变特征对积分时长的敏感程度,故在处理那些与训练样本接近的考核样本时,效果较好,但泛化能力却并不理想。而且由于需要用小步长积分相当长的时段,故总计算量的减少并不令人满意。
完整的扩展等面积准则(EEAC)[6]由下面3种算法融合而成,即基于数学模型近似等值的静态EEAC(SEEAC)[7]、基于受扰轨迹严格映射的集成EEAC(IEEAC)[8],以及作为纽带的动态EEAC(DEEAC)[9]。SEEAC,DEEAC,IEEAC这3种算法都基于“将积分空间中的高维受扰轨迹向一系列映象平面执行保稳降维映射”的思路。其算法流程都是先获取多机受扰轨迹,并在受扰轨迹每个仿真步长处重新执行保稳降维的空间映射,将多机轨迹解耦为一系列正交的时变等值单机—无穷大母线(OMIB)系统的受扰轨迹,从中分别求取能量裕度,最后聚合为原多机系统的能量裕度。
这3种算法的区别是:求取受扰轨迹的方式与步长(映射步长则与之相同)依次减小。它们分别是单步泰勒级数展开、4步泰勒级数展开、小步长数值积分;在各自对应的受扰轨迹精度的含义下,它们提供的稳定裕度都忠实地反映了相应受扰轨迹的稳定裕度。给出的稳定裕度ηSE,ηDE,ηIE的精度及计算量都依次增加。其中,SEEAC算法具有解析解,计算量可忽略不计,但误差却难以保证;IEEAC算法则采用全模型、足够小的积分及映射步长,所以较慢。需要再次强调的是,在精确积分给出的受扰轨迹的含义下,IEEAC严格地反映了系统的同步稳定裕度。
对含有电力电子装备的电力系统,其被大量换流器解耦为机械转动惯量相互独立的众多子系统。暂且将内部没有同步机者标记为A型子系统,而将含有同步机者标记为B型子系统。两者的复杂交互对系统行为的影响包含2个侧面,即电磁过程对机电过程(A对B)的影响,及机电过程对电磁过程(B对A)的影响。这2个问题所研究的最终目标变量完全不同,所以在数值积分后,不可能用同样的方法提取各自的量化指标[10]。A对B的影响是指在电力电子装置影响下,常规机组间的稳定性问题,EEAC理论完全适用于此;只要受扰轨迹能正确反映电力电子装置的影响,EEAC算法就一定能正确量化[6]。但是,研究B对A影响的问题,则本来就不是EEAC的目标领域。
作为IEEAC及SEEAC之间的过渡环节,DEEAC算法采用大步长泰勒级数展开求取故障中及故障后的受扰轨迹,故各种性能均处于SEEAC及IEEAC之间。由于完整的EEAC的精度是由IEEAC来保证的,因此DEEAC只会影响整个EEAC算法的整体计算量,而不会影响最后的精度。DEEAC部分地计入了时变因素的影响,并将解析求解的SEEAC与精确求解的IEEAC链接为完整的EEAC算法链。其作用是:①减少搜索主导映象时的迭代次数; ②为IEEAC提供更好的初值;③使完整的EEAC算法充分集成IEEAC的精确性与SEEAC的快速性。由于DEEAC本身的计算量仅为少量次数的泰勒级数展开,故大大提升了EEAC的整体性价比。
“主导映象系统呈现理想的哈密顿特性”,这是指该映象系统在任何一个时段内的等值系统都具有相同的映象系统参数。已经证明:对于这样的算例,3种算法将给出完全相同的稳定裕度值,即ηSE=ηDE=ηIE。
映象系统的非哈密顿特性来自互补群各自群内的功角非同调性及电压非同调性。基于“误差与积分(及映射)步长之间呈正相关”的规律,根据ηSE与ηDE之差,可以定性地将ηDE与ηIE之差(即ηDE的误差)按大小分类。据此,可以从大量学习算例中采用机器学习技术训练分类器。若大部分的稳定算例不再需要计算ηIE,总计算量就可大大减少。
文献[11]设计了算例筛选的分层框架及反映稳定算例充分条件的3个判据,可以强壮而高效地识别无风险算例;文献[2]进一步应用大数据技术,将算例筛除的功能扩展到故障支路两端不同时开断的场景。
DEEAC(nd+np)所标记的是:采用步数为nd(及np)的泰勒级数,求取故障中(及故障后)受扰轨迹的DEEAC算法。显然,SEEAC就是DEEAC(1+1);IEEAC就是nd=Td/Δt,np=Tp/Δt的DEEAC,其中Td和Tp分别为故障中和故障后的时长,Δt为积分步长。
DEEAC(2+2)分段方案已被沿用了30年,但它的分段方案(nd+np)对EEAC的整体性能的影响,以及对算例筛除率的影响却还未被透彻地研讨过。显然,增加nd或np,都可以提高ηDE的精度,但当步数增加到一定程度后,精度就不再显著提高。而计算量却将一直呈线性增加,故nd及np的值需要优化。
故障期间,主导映象的互补群群内各机组的功角非同调性还不明显,主导映象系统的时变性不会很强。大量仿真也证实,沿用以前的nd=2可达到最佳的性价比。因此仅需优化DEEAC(2+np)算法中的np值。
本文探究主导映象在故障中及故障后的时变特性,提出自适应分段映射的DEEAC算法。针对9个实际系统在多工况下的大量对称及不对称故障,随机抽样;从中筛选出195个强时变的算例,以研究np对DEEAC(2+np)分析精度和速度的影响。据此设计自适应分段的DEEAC算法,即根据DEEAC(2+2)与SEEAC所得稳定裕度之差来标注目标算例的时变度,并只对强时变的算例采用DEEAC(2+5)算法。仿真验证了该自适应分段映射方法,以较小的计算增量为代价,大幅提高了DEEAC的分析精度。
1 DEEAC(2+2)算法及其贡献
1.1 DEEAC(2+2)算法的提出
基于模型聚合技术的SEEAC算法巧妙地将等面积准则应用于多机电力系统暂态稳定的快速评估中,其快速性从未受到质疑。但在实际大电网中出现的大误差算例表明:必须正视微分代数方程在降阶等值后的时变特性,而不能回避实际受扰轨迹的求取[6]。由此,文献[9]提出了传统的DEEAC(2+2)算法。
DEEAC(2+2)算法在故障中及故障后采用“2+2”分段的泰勒级数展开获得受扰轨迹,并相应更新映象OMIB系统的时变参数。从而将采用“1+1”分段的泰勒级数、基于模型聚合的SEEAC算法变更为轨迹聚合。附录A中的图A1针对一个暂态失稳的多群系统,比较了由SEEAC和DEEAC(2+2)算法执行量化分析时的功角(Pe-δ)曲线。不难看出,即使只更新了映象参数2次,时变因素的影响已被粗略计及,而增加的计算量却微乎其微。
1.2 DEEAC(2+2)算法的桥梁效应
DEEAC(2+2)算法在计算中共享了SEEAC算法的部分计算,但也修正了由SEEAC算法提供给IEEAC算法的计算初值,以加快收敛到临界条件。DEEAC(2+2)算法的速度非常接近SEEAC,而比IEEAC算法要快得多,为原本水火不容的分析精度与速度提供了协调的可能。
DEEAC(2+2)算法丰富了EEAC算法框架。由于部分计及时变因素,因此利用它与完全忽略时变因素的SEEAC算法结果之间的差别,可以反映算例时变程度的强弱,进而通过为DEEAC(2+2)算法的最大误差范围设定保守的阈值,可以筛选出相当大的一部分算例,不必再通过IEEAC计算。由于DEEAC(2+2)算法同SEEAC算法的计算量都很小,因此可在保证零风险性误判的前提下大大提高分析效率,从而巧妙地协调好计算的精确性与快速性[2]。
2 DEEAC(2+2)算法还不够精巧
2.1 在强时变算例中的表现
DEEAC(2+2)算法在一定程度上计及了时变因素的影响,大大弱化了SEEAC算法对互补群群内同调性假设的依赖。但对具有强时变性的算例,仍有可能产生定性误判。
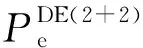
2.2 在不同时段内选用不同的分段数
增大nd及np,可以更好地反映算例的时变性,但也增加了计算量。协调的思路之一是采用不同的nd及np;思路之二是根据具体算例的时变特性,自适应地选择分段数。
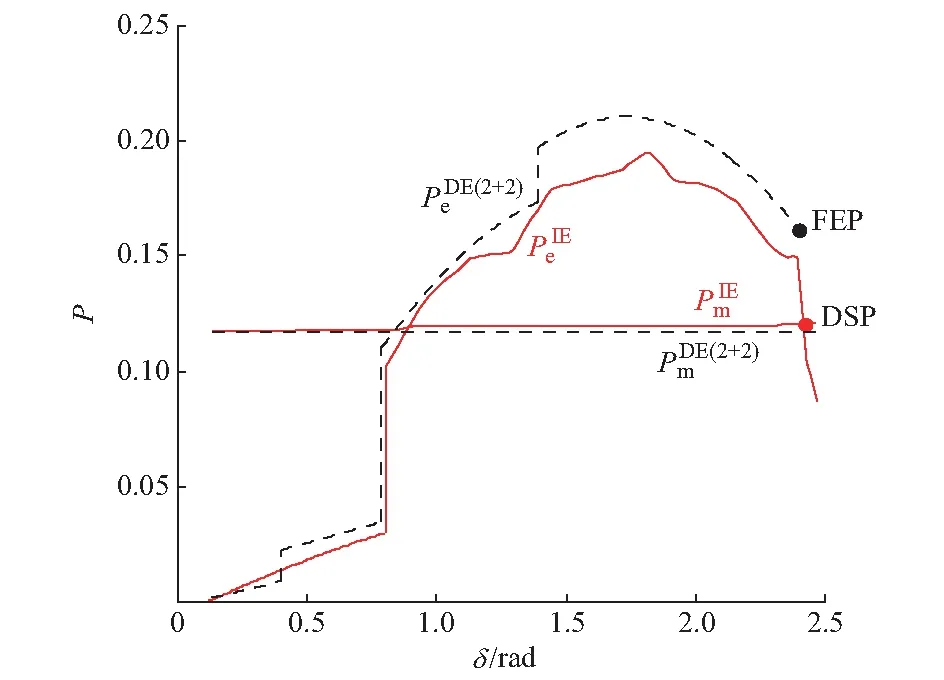
图1 DEEAC(2+2)算法与IEEAC算法给出的P-δ曲线Fig.1 P-δ curves obtained by DEEAC(2+2) and IEEAC algorithms
附录A中的图A2为西北系统(2010年数据)陕渭南—陕北郊回路1三相短路时的摇摆曲线,深色及浅色曲线分别表示领前群及余下群机组。t1=0.31 s故障清除,t2=1.11 s主导映象系统遇到DSP。故障期间,领前群及余下群的群内同调性相对较好;故障清除后阶段,余下群机组表现出较明显的相对振荡,时变程度明显强于故障中。此规律的普适性在不同的系统及工况中得到验证。
2.3 分段数的自适应
为了有效构建具有自适应分段映射的DEEAC算法来协调分析精度与速度,必须掌握主导映象的时变性分布规律,仅在时变性强的时段内适当增加分段数;掌握分段数对分析精度和速度的影响规律,优化自动分段方式。为了保证自适应的强壮性,必须考虑不对称故障及故障支路两端先后开断后的场景。
3 主导映象在暂态过程中的时变性分布规律
3.1 暂态过程的不同阶段
在支路开断时刻(τ),电网拓扑的变化引起节点电压、电流,及转子加速度的突变,将暂态过程划分为2个或更多个时段。
3.2 各阶段时变程度的表征
在故障中的时段内,即使主导映象的互补群各群内机组的加速度存在明显差别,但由于转子间的速度差还未显著积累,故功角差的变化尚不明显;由于主导映象的互补群中,各群内的非同调性不会很强,可以采用大步长泰勒级数展开求取受扰轨迹。而在故障后的时段内,群内非同调性可能已充分发展,大步长泰勒级数展开引入的误差可能较大。
文献[11]根据DEEAC(2+2)及SEEAC计算结果之差构造了算例的时变度指标。通过单独改变某一时段内的参数更新次数,可以掌握该时段内时变程度的强弱。
以ek,di,j表示算例k,保持np=2,而nd由i增加为j时的敏感程度,即算例k在故障期间的时变程度,如式(1)所示:
(1)
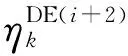
类似地,式(2)中的ek,pi,j表示算例k,保持nd=2,而np由i增加为j时的敏感程度,即算例k在故障清除后阶段的时变程度。其他符号则可类推。
(2)
3.3 故障中及故障清除后阶段时变程度的比较
以DEEAC(2+2)为参考,保持非研究阶段的分段数不变,仅增加研究阶段的分段数,按式(1)或式(2)给出的均值来量化研究阶段的时变程度。
测试算例的全集(SU)包含下述系统及工况下的三相对称及不对称故障:海南(2009年数据)、山东(2004年及2012年数据,分别记为山东A及山东B)、江西(2011年数据)、浙江(2012年及2013年数据,分别记为浙江A及浙江B)、河南(2011年数据)、新疆(2012年数据)和南方电网(2012年数据)等9个系统的原始工况及全部注入量增大5%的修改工况。故障清除时间在0.08~0.50 s之间随机抽样,共1 652个三相对称故障算例,1 620个不对称故障(单相接地、两相接地、两相相间短路)算例。
3.3.1故障期间的时变程度
对任一算例k,固定np为2,将nd由2到6依次增加,分别计算稳定裕度,据式(1)计算其敏感程度的平均值。按不同故障类型、研究系统及工况分别进行统计,最终得到测试算例全集的统计结果,如附录B中的表B1及表B2所示。从中可见,不同系统的时变程度有较大差异,但统计的范围越大,则差异越小。这个统计规律对于对称故障及不对称故障均符合。
3.3.2故障清除后阶段的时变程度
采用类似方式,评估了全部算例在故障清除后的时变程度。其结果示于附录B中的表B3及表B4。不论在什么范围内的统计值,对称故障的时变程度都要比不对称故障的时变程度大。
3.3.3故障中及故障后时变程度的强弱比较
从统计分析的视角,无论在什么范围内的统计值,故障清除后的时变程度都要比故障期间的时变程度大得多,有的甚至达到一个数量级。其中的因果关系是:随着时间的积累,不同映象系统之间的能量交换越来越大,表现为非哈密顿因素的影响越来越强烈。
为了以较小的计算代价增量换取较大的分析精度提升,应该在时变程度强的时段,即故障清除后的时段内增加映射步数。
4 np影响计算速度和精度的规律
4.1 测试算例子集的选取
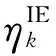
εth
(3)
当εth取为0.69时,在SU的1 652个对称故障算例及1 620个不对称故障算例中,分别有103及92个算例被识别为强时变的算例。需要说明的是,不同的εth值会影响测试算例子集SS的工作量及结果显示的清晰度,但εth取为0.69时,已经将DEEAC(2+2)算法会定性误判或接近误判的所有算例包含在内,因此没有必要由于进一步减小εth值,而造成研究工作量的增加。
4.2 计算速度及精度随着np变化的规律
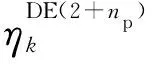
(4)
4.3 计算速度与计算精度的关联性
图2(b)则以np为隐参数,给出计算速度与计算误差之间的相关性。np在整数集{2,3,4}内增加时,平均计算量线性增加,而平均误差呈近乎线性地减小;np在整数集{4,5}内增加时,平均计算量仍然线性增加,而平均误差仅稍有减小。根据图2(b),可按对误差和速度的不同偏好选择恰当的np值。
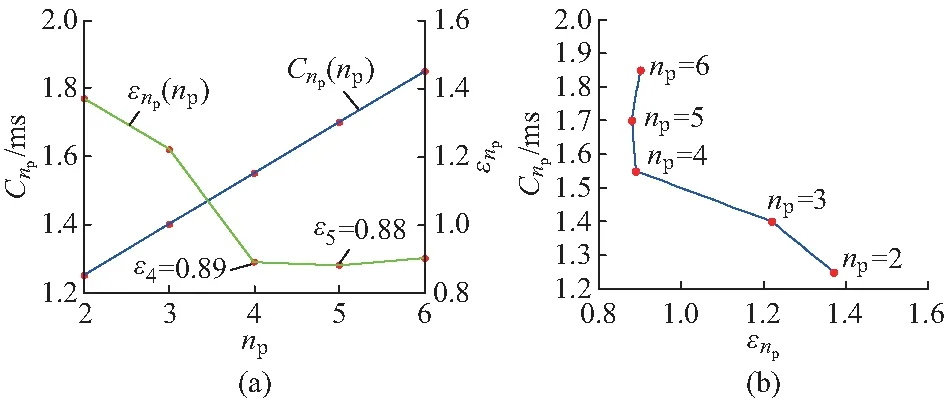
图2 np对计算速度及精度的影响以及计算速度与计算误差的关联性Fig.2 Influence of np on computational burden and accuracy as well as relevance of the computational burden and the error
5 兼顾分析精度与速度的np
5.1 对np的建议
对算例集SS的平均效果来说,np由2增至4时,单位计算量的增加对分析精度的提升较大,而从4增至6时,则性价比较低。下面再从单独算例的误差分布概率来仔细分析。
图3(a)(或图3(b))针对np取4(或5)时,给出了SS中各算例的计算误差εk,np的概率分布。其中,红线(对应于εk,np=1)右侧为DEEAC(2+np)算法单独评估时可能发生定性误判的算例分布。显然,np取5更恰当,虽然最终的精度都是由IEEAC来保证的。
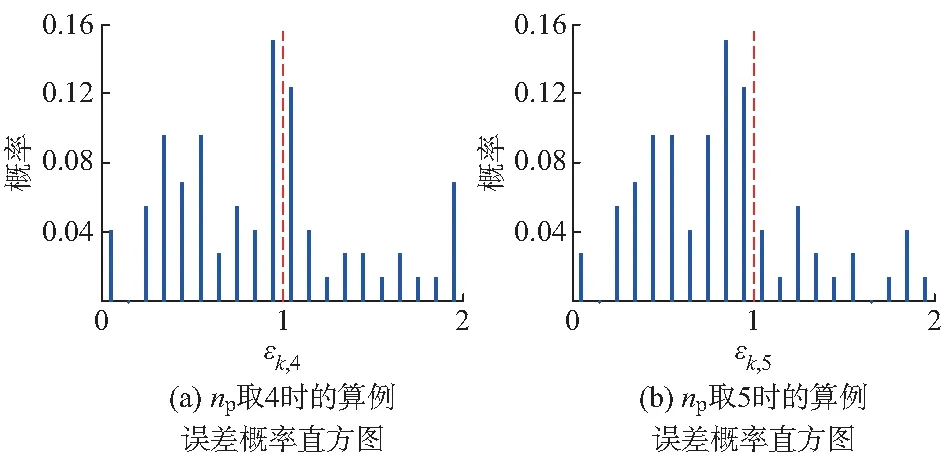
图3 算例误差概率直方图Fig.3 Probability histogram of analytical error
5.2 DEEAC(2+5)算法的效果
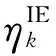
×100%
(5)
统计结果列于表1。定性来看:针对对称(或不对称)故障,DEEAC(2+5)算法单独判稳时的定性误判率比DEEAC(2+2)算法减少了50%(或77%);定量来看,平均精度则提升了21.8%(或29.7%)。
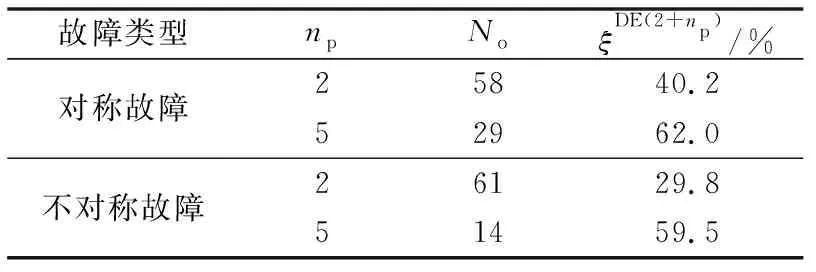
表1 DEEAC(2+5)算法的效果Table 1 Effect of DEEAC(2+5)
6 时变度控制下的自适应快速暂态稳定分析算法
自适应的策略为:①对子集SU
6.1 时变指标的选择
显然,采用IEEAC的结果来构造时变指标是本末倒置。文献[11]利用ηSE和ηDE(2+2)间差异,提出时变性指标σ1(τ)以反映故障中及故障后时变程度的强弱。基于统计分析将对应于σ1(τ)的阈值γ相对保守地设定为0.75,可以保证若某算例σ1(τ)≤γ,则必然不属于SS;而若某算例σ1(τ)>γ,则未必一定属于SS。
6.2 自适应EEAC算法
采用自适应DEEAC来连接SEEAC及IEEAC,进一步辅以算例筛除流程[11],可构成自适应分段的完整EEAC流程,如图4所示。
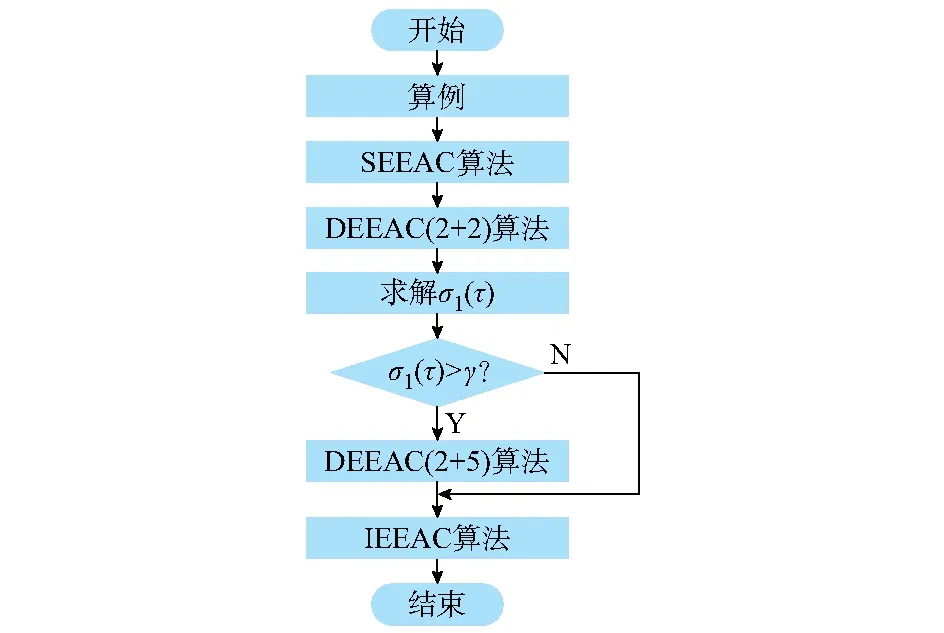
图4 基于自适应分段的EEAC算法流程图Fig.4 Flow chart of adaptive piecewise EEAC algorithm
6.3 计算性能的校核
表2给出按图4所示流程(尚未计入稳定算例筛除功能),对全部3 272个算例执行分析的统计结果:所需的计算量比全部应用DEEAC(2+2)算法时增加了3.98%,但大大提升了DEEAC的精度。

表2 分析结果的统计Table 2 Statistical results of the proposed TSA algorithm
7 结语
DEEAC(2+np)将解析的SEEAC与精确的IEEAC融合为一体。增加np,会在少许增加DEEAC的计算量的同时,改进IEEAC的初值。对于强时变的算例,这可能降低整体计算量。因此,可以根据具体算例的时变性,自适应地选择np值。
以DEEAC(2+2)与SEEAC的结果之差为指标,反映具体算例的时变性强弱。对于弱时变者,可以直接输出DEEAC(2+2)的结果;否则,通过DEEAC(2+5)算法向IEEAC提供初值。对9个实际系统中的三相对称及不对称故障进行测试,验证了该自适应分段DEEAC算法的强壮性。与DEEAC(2+2)相比,自适应DEEAC在增加不到4%计算量的代价下,可在维持弱时变算例分析精度的同时大大提高强时变算例分析精度,对2类故障中的强时变算例的分析精度分别提升了21.8%和29.7%,定性误判数则分别减少50%和77%。
为将文献[11]提出的稳定算例筛除功能融入,可在本文图4执行“IEEAC算法”之前,插入“稳定算例筛除”的步骤。这样做的益处是:①对于强时变算例,用DEEAC(2+5)替代DEEAC(2+2)做IEEAC的初值,可以减少IEEAC在处理强时变算例时的搜索次数;②对于弱时变算例,用DEEAC(2+5)替代DEEAC(2+2)直接输出结果,则也将提高最后结果的精度。
本文受南瑞集团有限公司科技项目“综合能源系统仿真评估关键技术研究”资助,特此致谢!
附录见本刊网络版(http://www.aeps-info.com/aeps/ch/index.aspx)。
