梯级水电站群中长期优化调度的离散梯度逐步优化算法
2018-11-26赵志鹏廖胜利程春田钟儒鸿王昱倩
赵志鹏,廖胜利,程春田,钟儒鸿,王昱倩
(1.大连理工大学,辽宁 大连 116024;2.华能澜沧江水电股份有限公司,云南 昆明 650206)
1 研究背景
截止到2016年底,我国水电装机容量和年发电量已经突破3亿kW和1万亿kW·h,分别占全部能源的20.9%和19.4%[1],水电已经成为中国占比最大的可再生能源[2]。充分利用水电资源,进行水库群优化调度是构建清洁低碳,安全高效的现代能源体系的重要措施[1]。梯级水电站群优化调度是一个典型的高维度、多阶段、非线性、非凸优化问题[3],其求解难度随着电站数量的增加,相互制约约束条件的引入,复杂电力和水力联系的耦合而急剧增加。目前常用的求解方法包括线性规划[4]、非线性规划[5]、网络流[6]、大系统分解协调方法[7]、动态规划及其改进算法[8-10],以及以遗传算法、粒子群算法、差分进化算法等为代表的新兴智能算法[11-14]等。线性规划,大系统分解协调,网络流等方法都需要对系统进行一定的近似处理,容易产生偏差;非线性规划对约束条件和目标函数的函数形式有一定的要求,难以应用于实际;智能算法,由于随机因素的存在,其解稳定性较差。动态规划因其对约束条件和目标函数的函数形式限制较少,结果稳定等特性,是水库调度领域应用最广泛的算法之一,但是随着计算规模的增加面临着严重的“维数灾”问题。
逐步优化算法[15](Progressive Optimality Algorithm,POA)作为动态规划的改进算法,将多阶段问题转化为多个两阶段问题,降低了阶段间的状态组合数目,被广泛应用于水电优化调度[16-19]。在求解两阶段子问题时,POA采用给定离散步长的网格搜索法,确保了在求解子问题上的全局收敛性,但随着规模的增加,仍然存在严重的“维数灾”问题。针对此问题,已有文献将POA算法与正交抽样[18]、逐次逼近算法(DPSA)[20-21]、并行计算[22]等方法进行组合优化,使“维数灾”问题得到缓解。POA算法中的两阶段子优化问题实质上是一个多变量单值函数的最优化问题。本文提出离散梯度(Discrete Gradient)的概念,并利用离散梯度下降法对子优化问题求解,从而提出离散梯度逐步优化算法(DGPOA)。该方法可在不直接求导的情况下,使用离散梯度的信息,确定给定离散步长下的最优搜索方向,并利用线搜索迭代方程进行迭代求解,可以显著减少计算规模,快速获得优化结果。
2 调度模型
2.1 目标函数以发电为主的中长期优化调度一般采用发电量最大模型。本文计算步长选为1个月,调度周期为1年。
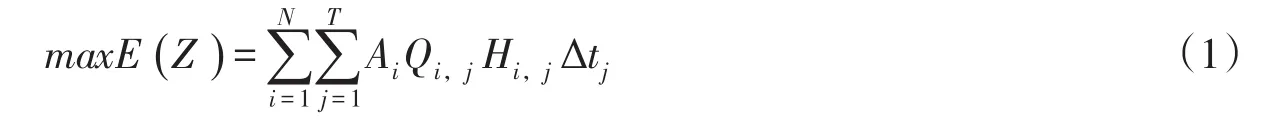
式中:i、j分别为水库和时段序号;N为参与计算的水库总数;T为总时段数,本文设置为12;E为总发电量(kW·h); Ai为水库i的出力系数;Hi,j为水库i时段j的平均净水头(m);Δtj为时段j的小时数(h);Qi,j为水库i在时段j的发电流量(m3/s)。
2.2 约束条件
(1)始末水位约束:

(2)水位上下限:

(3)出力上下限:

(4)水量平衡方程:
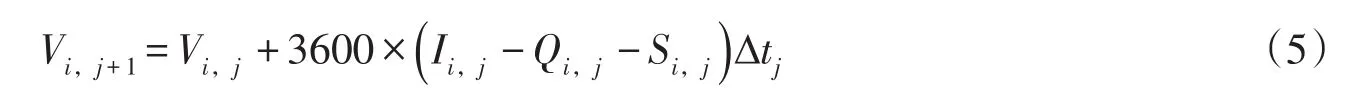
其中

式中:Vi,j为水库i时段j的末库容(m3); Ii,j、 qi,j、 Si,j分别为水库i 时段j的入库流量、区间流量以及弃水流量(m3/s),其中qi,j为已知;Ωi为水库i的直接上游水库集合,对于龙头水库Ωi为空集。
(5)发电流量限制:

(6)出库流量限制:

3 逐步优化算法
POA算法将多阶段问题转化为多个两阶段问题,求解时固定其他时段,仅对求解的两时段问题进行优化计算。计算结果作为其他时段的初始解,如此逐个时段求解,直到收敛。计算步骤如下:(1)确定各水库在调度期内的初始水位过程,调度阶段总数设为T,令E等于初始水位过程发电量。(2)设t=T-1。(3)固定其他调度时段,优化各水库水位Zi,t,使t阶段和t+1阶段梯级发电总量E(Z1,t,Z2,t,…,Zn,t) 达到最优。(4)令t=t-1,如果 t≤ 0,则转至步骤5,否则转至步骤3。(5)计算本轮优化所得的总发电量E′,判断| E-E′|<ε是否成立,如果成立,认为算法收敛,终止计算,输出结果。否则令E=E′,转至步骤(2)。
步骤(3)实质上是一个有约束的多变量单值函数的最优化问题。对于此问题,POA算法采用给定离散步长的网格搜索法求解子优化问题。当水库数量较少时可以在子优化问题中获得较为精确的全局最优解,然而随着水库数目的增加,计算规模呈现指数增长[23],面临严重的“维数灾”问题。为解决该问题,本文使用离散梯度下降法解决步骤(3)的子优化问题,并提出离散梯度逐步优化方法(DGPOA)。
4 离散梯度逐步优化算法
4.1 梯度下降法梯度下降方法是无约束优化问题中最常用的方法之一。设函数 f:Rn→R,如果在每个变量xj均具有偏导数,则对于无约束最优化问题:

负梯度方向-∇f()xn为其最速下降方向,序列x0,x1,x2,…,满足:

可得:

对于凸函数,序列(xn)会收敛到全局最优解,非凸函数会收敛到局部最优解。
4.2 离散梯度下降法使用梯度下降法的一个重要前提是函数 f(x)在求解域中是可导的。然而,对于水库梯级优化,大部分特征曲线(如水位库容曲线,水头耗水率曲线,尾水位泄量曲线等)为实测点集形成的分段函数,而约束条件和目标函数则为这些特征曲线的非线性组合,难以直接求导。为了充分利用局部区域的梯度信息,优化搜索方向,加快搜索速度,本文结合水库调度的特点,提出给定离散步长下的离散梯度的定义及计算方法,以及其对应的离散梯度下降法。
4.2.1 离散梯度计算 对于多变量单值函数 f(x1,x2,…,xn),给定离散步长h>0的情况下,令:
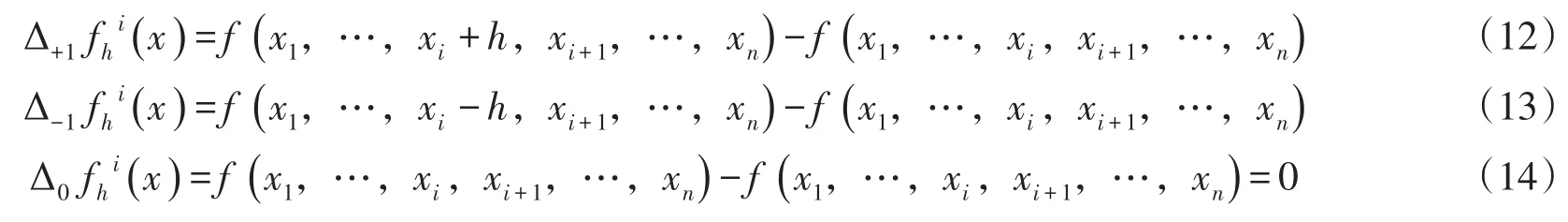
定义1。离散步长h下的近似偏导数:

该近似偏导数有如下性质:

在定义1的基础上,可以进一步定义离散梯度。
定义2。给定离散步长h下离散梯度:
如果 f在x=a点存在梯度,则有:

4.2.2 搜索步长的确定 对于水库调度,优化的状态变量(如水位)和目标(如发电量)常常具有不同的量纲,导致步长容易出现过大或过小的情况,继而影响算法收敛和搜索速度。本文搜索步长根据离散步长h以及离散梯度值进行动态设置。
设:

则设搜索步长为

线搜索迭代方程为

4.2.3 停止准则

或者

对于离散情况,在某个精度下,有可能出现沿离散梯度负方向搜索函数值变大的情况,此时最优值一般位于an,an+1之间,认为已满足该精度要求,可以停止搜索。
4.3 库群中长期优化调度总体求解流程
(1)以水库水位作为状态变量,设置水位离散步长h,调度阶段总数T,发电量收敛精度ε。
(2)根据常规方法确定初始水位过程,令E为初始条件下的发电量。
(3)设置t=T-1。
(5)时段t的两阶段问题为有约束的最优化问题:

式中:多变量标量值函数P∶Rn→R,为阶段t的发电量函数,C为约束集。
使用罚函数为常数值函数的内罚函数法对约束进行处理。即当水位及由水位计算的关键量不满足约束时,发电量设置为-M,其中M为足够大的常数。
因此可定义函数 f∶Rn→R:
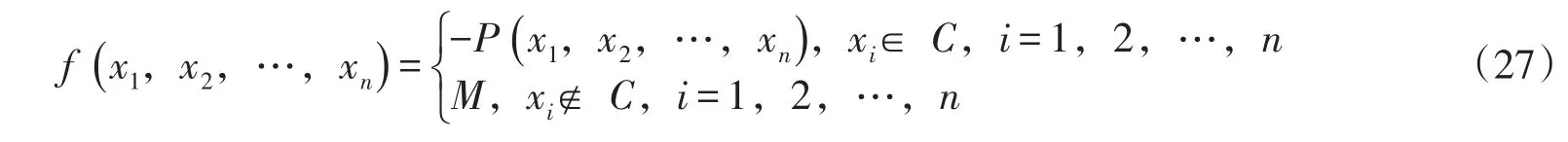
并将(25)转化为无约束最优化问题:

(6)令n=0,设置离散梯度下降法初始解a0=。
(8)判断t≤ 0,如果满足跳到步骤(9),否则返回步骤(4)。
(9)根据优化的水位计算发电量E′,判断|E′-E|≤ε,如果满足则输出结果,结束计算,否则令E=E′,返回步骤(3)。
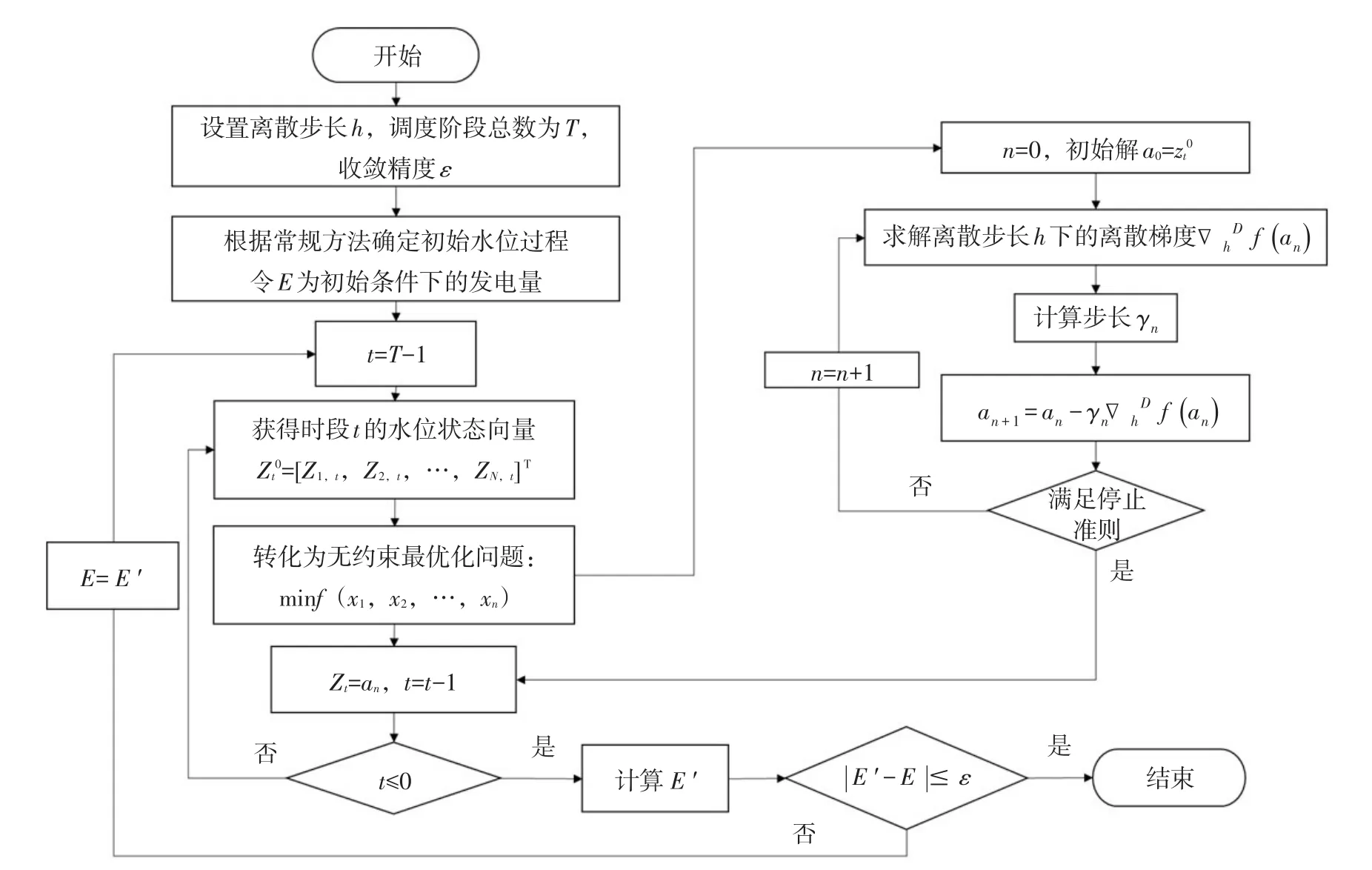
图1DGPOA计算流程图
流程见图1。
5 应用算例及分析
5.1 工程背景及参数选择以云南省澜沧江干流5座主要电站为例对本文模型算法进行验证。澜沧江流域水能资源丰富,是我国重点开发的13个水电基地之一。包含的5座电站从上游到下游依次为小湾、漫湾、大朝山、糯扎渡和景洪,总装机容量达到14700 MW,是云南重要的调峰调频电源及西电东送电源点。除小湾、糯扎渡为多年调节外,其余均为季调节,各水库基本情况和始末水位设置值见表1。模型算法采用Python语言编写,如果没有特殊说明,初始解均由等流量法生成,设置发电量收敛精度ε=0.001亿kW·h。
5.2 不同精度下的优化结果分析利用平水年数据分别使用POA、POA-DPSA[20-21]和DGPOA对澜沧江流域优化调度。方案1将澜沧江流域简化为小湾、糯扎渡两库系统,计算结果见表2。方案2对小湾、漫湾、大朝山、糯扎渡和景洪等五水库系统进行计算,计算结果见表3。两方案三种算法计算发电量随离散精度变化见图2。定义POA计算发电量e0,POA-DPSA计算发电量e1,DGPOA计算发电量e。POA-DPSA与POA计算发电量的相对偏差,DGPOA与POA计算发电量的相对偏差DGPOA与POA-DPSA的相对偏差
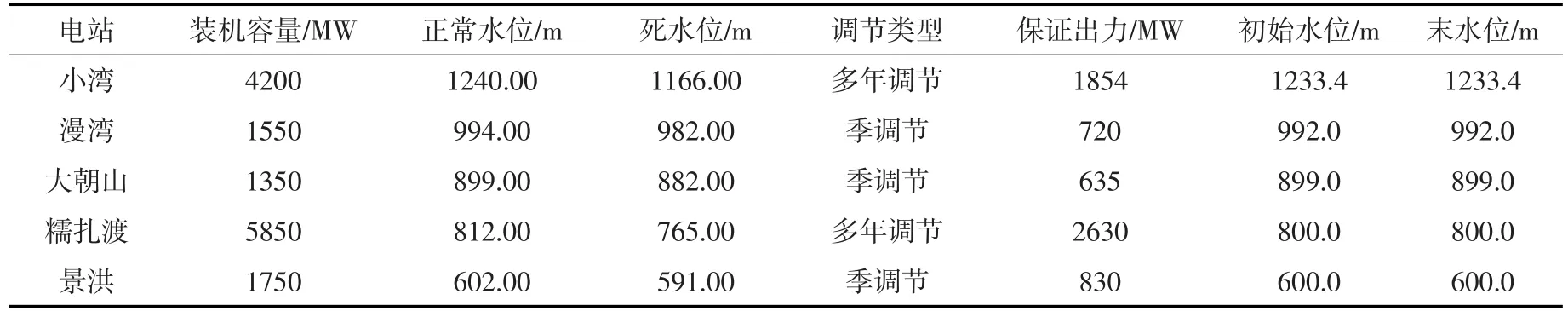
表1 澜沧江梯级水库基本情况与始末水位设置值

表2 方案1不同精度下POA、POA-DPSA、DGPOA发电量对比
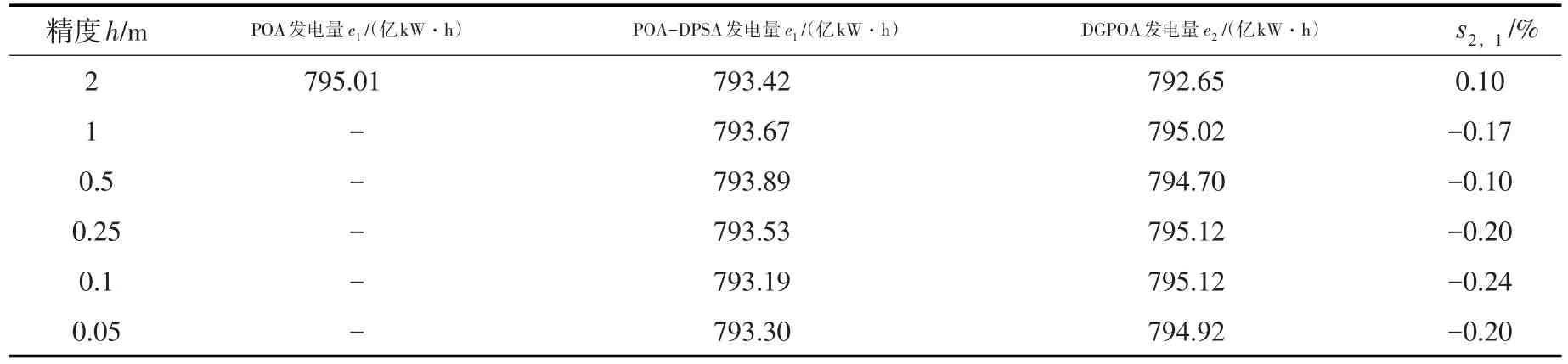
表3 方案2不同精度下POA,POA-DPSA,DGPOA发电量对比
从计算结果上可以看出,方案1两库系统中,POA发电量e0在各离散步长下均处于最优。POADPSA计算发电量e1在不同离散步长下依次为0.19%、0.24%、0.15%和0.21%,与POA相对差距总体在0.20%左右。DGPOA计算发电量e2与POA的相对差值则从0.53%逐渐减少到了0.17%。如图2(a)所示,DGPOA与POA-DPSA计算结果差距随着精度的提高逐渐减少,并且在精度为0.05 m时DGPOA计算结果要优于POA-DPSA。值得注意的是,并非离散步长越小,优化结果越好,POA在离散步长从1 m减少到0.5 m后优化结果反而出现了下降,而POA-DPSA最优值出现在离散步长为0.5 m的时候。这是由梯级水库优化调度问题的非凸特性导致的[24]。
方案2五水库系统中,POA在精度较高时,已经表现出了明显的“维数灾”问题,仅在h=2 m时可以在有限时间(1d)内计算出结果e0=795.01亿kW·h。如图2(b)所示,DGPOA计算结果在较高精度下要优于POA-DPSA计算结果。当离散精度h≤0.25m时,DGPOA计算结果要优于POA在离散精度h=2 m时的值。因此,DGPOA可以通过提高精度获得与POA算法相近甚至更好解。
5.3 不同精度下的求解效率分析方案1和方案2各精度下不同算法计算效率分别如表4和表5所示。将方案1和方案2离散精度和相应算法计算时间利用幂函数进行拟合,可得图3。定义POA计算时间为t0,POA-DPSA计算时间为t1,DGPOA计算时间为t2。
从计算时间上可以看出,方案1中各算法计算时间均随着离散步长h的减少而增加。在不同精度下,DGPOA算法计算时间分别是POA算法计算时间的2.01%、1.03%、0.40%、0.27%、0.09%和0.04%,相对POA算法的加速比t0/t2达到了50~250倍。DGPOA与POA-DPSA算法计算时间t2,t1的比值相对稳定,依次达到了13.70%、14.07%、11.33%、15.53%、12.99%和11.84%,加速比t1/t2可达7到9倍。方案2中,POA算法已经表现出了明显的“维数灾”问题,在精度h=2 m时的计算时间已经达到了4523.2s。在精度进一步提高后,其计算时间已经无法满足常规的使用要求。DGPOA计算时间相对于POA-DPSA分别占用17.89%、16.65%、13.01%、10.45%、5.22%和6.24%,计算加速比随着精度的提高有明显增加的趋势。
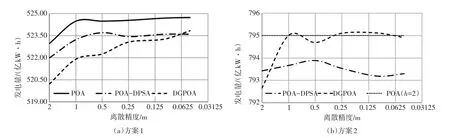
图2 各算法计算发电量随离散精度变化

表4 方案1各精度下不同算法计算时间对比
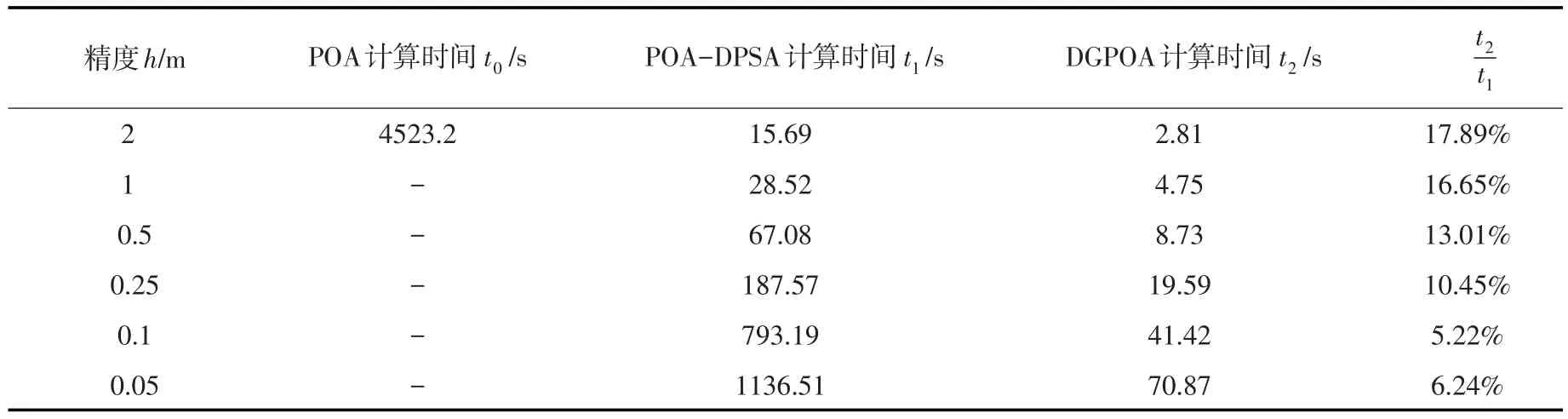
表5 方案2各离散步长下不同算法计算时间对比
如图3(a)所示,在方案1中,POA算法的计算时间大致与离散步长的平方成反比,POA-DPSA、DGPOA大致与离散步长的一次方成反比。这说明随着离散步长的减少,POA算法计算时间的增长速度将远超另外两种算法。这也体现出了线搜索类算法的优势。
如图3(b)所示,方案2中DGPOA计算时间大致与离散步长的0.9次幂成反比,DGPOA计算时间大致与离散步长的1.25次幂成反比。由此可得,随着精度的提高DGPOA相对POA-DPSA的计算速度优势将更加明显。
3种算法搜索过程有所不同,POA-DPSA算法采用了坐标方向的线搜索,不需要对网格内所有解进行遍历,“维数灾”问题相较于POA有所缓解。DGPOA相对POA-DPSA和POA,利用了局部离散梯度信息,在优化方向上进行优化,搜索路径更短,极大提高了搜索速度。
5.4 不同初始解下的结果分析采用不同配比的出库流量生成小湾,糯扎渡双库系统的初始水位解,并以此为基础分别用POA、POA-DPSA和DGPOA算法进行水库优化调度。其中离散步长h均选为0.05 m。澜沧江流域根据径流特征可以分为汛前期(1—5月)、汛期(6—10月)和汛后期(11—12月)。初始解根据各时期各月给定配比的出库流量求出。各时期各月出库流量配比及计算结果见表6。其中初始解e的流量配比等价于等流量法,即同一水库各月出库流量均相同。
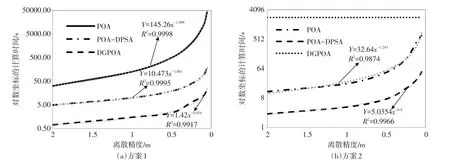
图3 计算时间与离散精度关系

表6 初始解生成方式及计算结果
不同流量配比会生成不同的初始解,不同初始解下的计算结果可以反映算法的全局搜索能力。从计算结果上看,POA算法在初始解a—h下计算结果均为524.7亿kW·h。POA-DPSA算法在初始解a—f下计算结果均为523.59亿kW·h,在初始解g和h下,计算结果有少量提高,分别为523.72亿kW·h和523.86亿kW·h。DGPOA算法在初始解a—h下随着汛期各月份流量配比提高,计算结果从522.70亿kW·h提高到524.04亿kW·h,总体优于POA-DPSA。在初始解i和j下,3种算法计算结果均出现了明显下降,下降幅度DGPOA最大,POA-DPSA其次,POA最小。由此可得,POA算法求解结果总体更优,对初始解依赖相对较少结果相对稳定,全局搜索能力最强。POA-DPSA算法和DGPOA各有优劣。如果初始解为随机生成,在与最优解差距较大时,POA-DPSA结果相对稳定。而在POA算法常用的初始解生成方法(等流量法)及其相邻搜索域(初始解d—h),DGPOA搜索效果相对更好。
5.5 不同来水条件下的结果分析分别采用枯水年(75%)、平水年(50%)和丰水年(25%)径流资料和POA-DPSA和DGPOA算法对澜沧江流域5个主要水库进行优化调度。由于POA在5个水库系统中已经表现出了严重的“维数灾”问题,此处不再对其进行计算。离散步长h都选为0.1 m。优化结果见表7。从计算结果上看,DGPOA算法和POA-DPSA算法在枯水年分别为710.24亿和710.31亿kW·h,丰水年分别是877.93亿和878.07亿kW·h,POA-DPSA整体较优但差距不大。在平水年,DGPOA计算结果则要优于POA-DPSA,发电量分别为794.85亿和793.19亿kW·h。
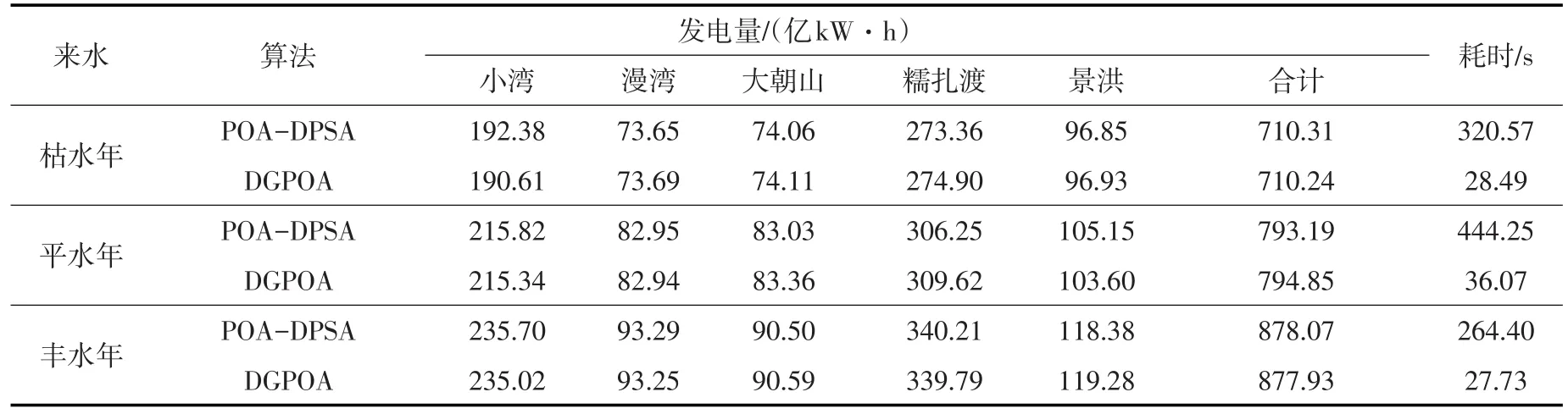
表7 不同来水条件下各算法计算结果对比
从计算效率上看,在枯水年、平水年和丰水年水平下,DGPOA算法的计算时间t2分别为28.49、36.07和27.73 s,POA-DPSA算法的计算时间t1分别为320.57、444.25和264.40 s,加速比t1/t2达到了9~12倍。年平均水平DGPOA算法优化调度结果见图4。

图4 平水年下DGPOA算法的优化调度结果
从图4可以看出,两个多年调节水库小湾和糯扎渡在汛前均加大水位削落,充分发挥了调节库容,对其他水库进行补偿调度。进入汛期后,小湾和糯扎渡开始蓄水以保证汛后期的高水位运行。漫湾、大朝山和景洪3个季调节水库,在小湾和糯扎渡的调蓄下,始终处于高水位运行状态,确保了梯级的整体发电效益。
6 结论
为解决水电站群中长期优化调度的“维数灾”问题,在提出离散梯度的概念基础上,使用离散梯度下降法对POA两阶段子优化问题进行求解,提出了离散梯度逐步优化算法。该方法对待求问题的函数形式没有特别要求,可利用局部离散梯度信息,最优化搜索方向,快速获得优化结果。在澜沧江流域五水库系统多方案的计算结果表明,在工程常规精度下,DGPOA在不显著降低全局搜索能力的情况下,计算速度可达POA-DPSA算法的8~12倍,POA算法的50~250倍。并且随着水库数目的增加和计算精度的提高,其相对POA-DPSA和POA速度提升会更加显著。因此,DGPOA是解决水电站群中长期优化调度“维数灾”问题的有效算法。
