增湿情况重塑黄土非饱和渗透系数的测定方法研究
2018-11-26胡海军李常花崔玉军邵宗暄艾一丹
胡海军,李常花,崔玉军,邵宗暄,艾一丹
(1.西北农林科技大学 水利与建筑工程学院,陕西 杨凌 712100;2.同济大学 地下建筑与工程系,上海 200092;3.Ecole des PontsParisTech,LaboratoireNavier/CERMES,Champs-sur-Marne 77455 France)
1 研究背景
非饱和黄土的力学特性具有显著的水敏性,含水率增加会导致其强度降低和变形增加,因此降雨情况下黄土边坡稳定性的分析[1]、现场浸水试验情况下黄土地层湿陷变形的计算[2]均需要进行增湿情况下的非饱和渗流计算,获得地层中的水分分布。在非饱和渗流计算中,需要非饱和土渗透系数k和吸力s的关系或扩散度D和体积含水率θ的关系。农业和岩土工程领域的研究人员已经对土壤[3]、核废料缓冲材料[4]、压实土[5-9]等非饱和土的渗透系数或扩散度进行了大量试验测试研究,提出了各种确定非饱和土渗透系数或扩散度的方法。
类似测试饱和土渗透系数的直接方法有常水头方法和变水头方法,不同吸力下非饱和土渗透系数的直接测试方法也有稳态方法和瞬态方法两种方法。稳态方法通常较为耗时,且试验受到陶土板饱和渗透系数和进气值的限制,即不能测试渗透系数高以及吸力比较大的情况下的非饱和土渗透系数[6,10]。瞬态方法按水分迁移方向有垂直入渗或蒸发[7,9]、水平入渗[3,5,8]和毛细上升[4,6]等试验方法;按确定方法又分为瞬态剖面法[4,7,9]、Boltzmann 变换法[3,5,8,11-13]和浸润锋前进法[6,10]3种。
对于瞬态剖面法,已有研究表明该方法获得非饱和土渗透系数的精度与测试点间距[10,14]、测试时间间隔[14]和土性[10,14]有关,一般用于渗透时间较长的毛细水上升试验[6]、渗透系数很低的土体[4]或含水率测试点间距较小的垂直入渗再分布情况[9];非饱和黄土的渗透系数较大,其入渗时间相对较短,应用该方法时需要合理的水分测试点间距。对于Boltzmann变换法,该方法仅适用于水平入渗情况,所以本文进行了一维水平入渗试验,对3种方法的适宜性进行了研究。针对浸润锋前进法的水力坡降计算公式和Boltzmann变换法中的变换因子λ进行了改进,检验了改进后的效果,并与间接法(即采用拟合持水曲线的VG模型[15]和Brooks-Corey模型[16])获得的非饱和土渗透系数函数进行了对比,最后应用求解Richard方程的Hydrus软件采用不同方法所得的非饱和渗透参数,模拟了一维水平入渗试验,分析了预测浸润锋迁移距离和时间关系的精度,并根据数值试验研究了浸润锋前进法和Boltzmann变换法所采用的假定,对瞬态剖面法合适的测点布置位置和间距进行了研究。
2 水平入渗试验
2.1 一维土柱制备及仪器装置试验土料取自陕西省杨凌示范区党家村,该区域位于渭河三级阶地,为Q3黄土,天然密度为1.62 g/cm3,天然含水率为17.6%,颗粒比重为2.71,塑性指数为17.6。本文主要研究非饱和黄土渗透系数的测定方法,考虑到原状土较难制取,这里采用重塑土。制样土料质量含水率w=16.5%,土柱孔隙比采用黄土地层中常见的孔隙比e=1.1,直径为14 cm,考虑已有一维入渗试验土柱长度与直径比通常大于5[7],土柱长度采用90 cm。土柱共分18层、每层5 cm,击实而成,制样时根据目标孔隙比和土料含水率计算每层土料的质量,每层击到目标高度后均刮毛后再击下一层。整个试验装置如图1所示,有机玻璃管总长1 m,顶端10 cm放置带孔透水板后填充石子以作为渗透缓冲段,端部用环氧树脂将中心带输水管的有机玻璃圆板粘在有机玻璃管端面上。考虑到张力计有滞后效应,入渗试验仅应用ECH20水分仪(脚长约5 cm)测定各测点体积含水率而基质吸力由持水曲线计算得到,水分仪以15 cm等间距布置。有机玻璃管上水分仪的孔为长条形孔,制土柱时先将这些孔用塞子塞住,以防止制样时土从孔中漏出,当制样高度大于传感器高度时,将塞子取出,插入水分仪,并用橡皮泥密封水分仪与有机玻璃管间隙。马氏瓶用于提供与土柱最高点相同的恒定水位并用于获得入渗量信息。
2.2 测试仪器的标定为准确获得入渗过程中的入渗量和土柱各测点体积含水率,对马氏瓶读数变化与出水量的关系、水分仪读数与实际体积含水率的关系进行了标定。
马氏瓶总高1 m,内径为9 cm,在马氏瓶上贴刻度尺,获得出水量与刻度尺读数变化的比例关系,该比值为62.575 cm2,该值与马氏瓶内圆面积与马氏瓶内插管外圆面积之差接近,说明有机玻璃管断面基本均匀。
利用常规三轴试样制样器,制取与土柱相同初始含水率和孔隙比的试样,分别加水到不同含水率,用保鲜膜包裹,待水分均匀分布后,应用水分仪测试得到读数,然后应用烘干法测得质量含水率,根据干密度乘以质量含水率得到实际体积含水率,并考虑一维土柱入渗试验结束后各测点水分仪读数和实际体积含水率在内,建立了水分仪读数和实际体积含水率的关系。
2.3 持水曲线和饱和渗透系数测试应用浸润锋前进法和瞬态剖面法确定非饱和渗透系数需要一维入渗过程中各测点的基质吸力变化,其需要根据持水曲线计算得到,而Boltzmann变换方法得到的扩散度需由持水曲线转换得到渗透系数,因此对持水曲线进行了测试并应用VG模型[15]和Brooks-Corey模型[16]进行了拟合,另外为应用两个模型间接获得非饱和渗透系数函数,还测试了饱和渗透系数。
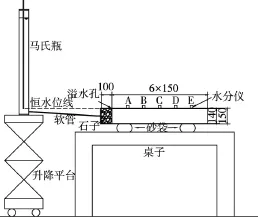
图1 一维水平入渗试验设备图(尺寸单位:mm)
一维土柱入渗过程为土体增湿的过程,因此制取了与土柱相同含水率和孔隙比的直径为14 m高为10 cm的小型土柱,通过埋入或插入的水分仪、土壤水势传感器MPS-6和张力计,测试了逐级加水、每级水分迁移稳定后的含水率与基质吸力值,另外为获得以上两种模型较为合理的残余含水率,还采用非饱和三轴仪应用轴平移技术测试了减湿三轴试样的吸力值。
对抽真空饱和试样和浸水饱和试样采用变水头法测试了饱和渗透系数,渗透系数分别为1.23×10-4cm/s和2.22×10-5cm/s,可见浸水饱和样渗透系数约是抽真空饱和试样的20%,抽真空饱和试样饱和度在95%以上,而浸水饱和样与一维入渗试验后土柱各测点处含水率接近,饱和度约为82%。文献[11]表明水平入渗试验存在类似于竖直入渗试验[17-18]中的饱和区、过渡区、传导区和浸润区,在入渗端面附近很小范围内存在饱和度接近100%的饱和区,随后有一段过渡区连接饱和区和传导区,传导区随着入渗时间的增加其长度增加,其饱和度基本不变,不同土类饱和度不同,但基本在70%~90%[11,17-18],传导区存在大量困陷气体[18],其吸力可认为等于0;文献[19]也指出土壤从初始含水率增湿到吸力为0时的饱和度小于100%,相应渗透系数建议取为完全饱和时的50%。大量的脱湿再增湿试验表明持水曲线具有明显的滞回性[20],即饱和的试样经历脱湿后再增湿到吸力为0时,饱和度低于100%。据此,本文把增湿到吸力为0时的困陷气泡和土颗粒材料考虑在一起,应用VG模型和Brooks-Corey模型拟合时,饱和含水率采用浸水饱和样的体积含水率0.43,所得持水曲线如图2所示,拟合所得参数如表1所示;应用间接法采用两个模型获得非饱和渗透系数函数时,饱和渗透系数采用浸水饱和样的渗透系数2.22×10-5cm/s,所得非饱和渗透系数函数如表1所示。
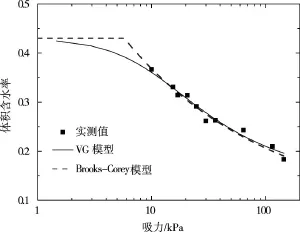
图2 增湿过程中的实测持水曲线点和VG模型和Brooks-Corey模型拟合持水曲线

表1 持水曲线VG和Brooks-Corey模型拟合参数和间接法确定的非饱和渗透系数函数
2.4 一维入渗试验过程首先应用升降平台提高马氏瓶位置,以使土柱前端石子段快速充满水,待位于土柱端面附近的溢水孔出水后,降低升降平台,使得其马氏瓶提供的恒水位线位于水平土柱的最高点,然后用橡皮泥封堵溢水孔,记录此时的时间作为入渗开始时间。试验过程中记录马氏瓶读数,水分仪读数则由采集装置每分钟采集一次,各测点基质吸力变化由其体积含水率根据VG模型持水曲线函数计算得到。
3 测试结果及不同方法确定的非饱和渗透系数
3.1 体积含水率变化应用水分仪读数与实际体积含水率之间的标定关系,获得入渗试验过程中各测点体积含水率随时间的变化时,发现各测点初始值和最终值分别与制样土料和试验完成后各测点烘干法换算得到的体积含水率有一定的差异,据此,对根据标定关系所得体积含水率再按式(1)进行修正:

式中:θc表示根据标定关系所得的体积含水率。θic和θim分别表示初始时各测点水分仪换算所得体积含水率和制样土料实际体积含水率,θfc和θfm分别表示试验结束时各测点水分仪换算和烘干法所得体积含水率。
最终获得的入渗过程中的各测点体积含水率变化如图3所示。
3.2 不同方法确定的重塑黄土非饱和渗透系数以测点A为例,说明浸润锋前进法确定非饱和黄土渗透系数所采用的计算公式。t1~t2时间段通过测点A断面的水体体积等于如图4(a)所示的阴影部分面积乘以土柱断面面积,该方法采用平行四边形FGIH的面积近似代替阴影部分面积,其中I点为θ(xA,t1)和θ(xA,t2)的中点(注:具体推导过程见文献[6],此为推导结果的另一种描述),由此可得该时间段通过A断面的水流速度v如式(2a)所示;t1~t2时间段测点A断面的水力梯度,文献[6]用t2时刻A点和A点之后Δxf之间的水力梯度来表示,如图4(b)所示,并应用ψ(xA,t1)近似代替ψ(xA+Δxf,t2)(注:当水分剖面平行移动时,该假定严格满足,后文也会检验该假定),其中Δxf表示t1~t2时间段浸润锋前进距离,水力梯度计算公式如式(2b)所示,为提高水力梯度计算的精确性,借鉴文献[7]中水力梯度的计算方法,采用t1和t2时刻A点与其前后相应Δxf之间水力梯度的平均值,来代表t1~t2时间段该断面的水力梯度。具体表达式如式(2c)所示,其中t1时刻A点与A点前Δxf之间的水力梯度为it2,这里应用了与前面类似假定:ψ(xA-Δxf,t1)近似等于ψ(xA,t2);t1时刻A点与A点之后相应Δxf之间水力梯度为it1;t2时刻A点与A点之前或之后相应Δxf之间水力梯度为it3和it2。由达西定律k=v/i,便可得到该时间段平均吸力下的渗透系数。从式(2a)—(2c)可见,除测点的体积含水率变化和由VG模型换算的基质吸力变化外,还需要不同时刻浸润锋的迁移速率vf,由于本文试验土柱初始含水率较高,增湿过程不如低含水率土柱容易通过浸润后呈现的颜色差别来分辨出浸润锋位置[6],本文采用水分仪读数开始变化的时刻作为浸润锋到达水分仪测点的时刻,得到浸润锋位置和时间关系的5个数据点,应用文献[6]针对观测的浸润锋位置和时间的关系所采用的幂函数如式(3a)来拟合,得到a=0.171、b=0.7269,相关系数为0.998,有了该关系,很容易得到该方法所需的不同时刻浸润锋的迁移速率如式(3b)所示。
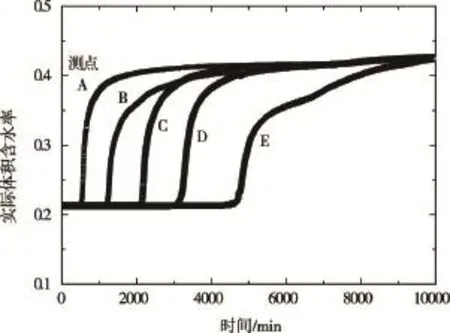
图3 一维入渗过程中各测点体积含水率变化

图4 浸润锋前进法计算渗透系数的原理

式中:xA为测点A离土柱顶端的距离,t1~t2时间段浸润锋前进距离Δxf可由该时间段内平均浸润锋迁移速率vf和时间段的乘积得到,其中浸润锋迁移速率为浸润区和非浸润区交界面即浸润锋的移动速率;ψ为基质吸力(单位为kPa),这里由VG模型持水曲线函数计算得到;θi为初始体积含水率。

式中:t单位为min,xf单位为cm,vf单位为cm/min。
同样以测点A为例,说明瞬态剖面法确定非饱和土渗透系数所采用的计算公式。如图5所示,这里只计算浸润锋到达B点之前的情况,而到达B点时,A点已经接近最终含水率,即可计算到很小吸力下的非饱和土渗透系数。在t1~t2时间段,通过测点A断面的水流速度如式(4a)所示,水力梯度计算公式如式(4b)所示,其他断面与此类似,只是计算水力梯度时要考虑前一测点的基质吸力。
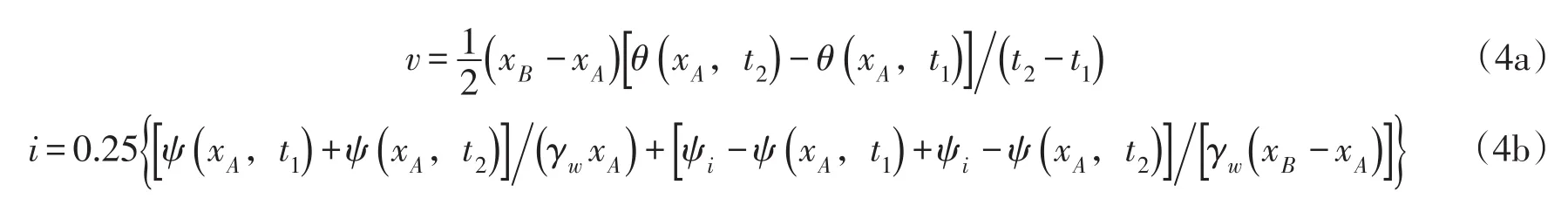
应用浸润锋前进法和瞬态剖面法确定非饱和渗透系数时,由于每分钟记录一次含水率,含水率数据密集,针对存在含水率不发生变化或变化很小的情况,舍去这些数据。获得的非饱和渗透系数如图6所示,需要说明的是在低吸力区,浸润锋已到达底部,这里仍绘制以作参考。应用VG模型和Brooks-Corey模型间接法获得的非饱和土渗透系数函数也绘于图6,可见浸润锋前进法与间接法确定的非饱和土渗透系数接近,而由于本文试验入渗速度较快且水分仪测点间距较大,瞬态剖面法得到的非饱和土渗透系数误差较大。另外图7给出了数据采用时间间隔较短情况下,浸润锋前进法中水力梯度计算公式改进前后所得不同吸力下的非饱和渗透系数,可见采用改进后的计算公式可较好地减少数据的波动性,特别是对低吸力区也可获得较为合理的渗透系数。
对于Boltzmann变换方法,其确定非饱和渗透系数的原理[11-12]为应用Boltzmann变量λ=xt-0.5化解一维Richard方程,获得扩散度的解析表达式如(5a)所示,可按式(5b)将积分转换为离散点求和[8,22],获得扩散度。


图6 瞬态剖面法和浸润锋前进法确定的非饱和渗透系数

图7 浸润锋前进法水力坡降计算公式改进前后所得的非饱和渗透系数对比

式中:λ=xt-0.5为Boltzmann变量,x为离入渗端面的距离,θi表示初始体积含水率,θw表示所求扩散度对应的体积含水率。
文献[13]表明固定时刻t,测定不同位置含水率,得到的λ-θ关系,与固定位置x,测定不同时刻含水率,获得的λ-θ关系很接近,即两种方法可得到一致的扩散度。本文采用的为后一种方法,针对5个测试点,整理得到入渗过程中各测点的λ-θ关系如图8所示,不同测点的λ-θ关系有一定的差距,其原因在于土柱制样的非均匀性、初始入渗边界条件并非严格满足(或初始入渗时刻的非准确确定)以及Boltzmann变量λ-θ关系离散性较大[23]。如果使Boltzmann变量λ-θ关系唯一,在浸润锋达到各测点时Boltzmann变量xft-1/2要为常量,也即要求式(3a)中幂函数的指数b为0.5,而式(3a)拟合所得的指数b为0.7269,尝试构造Boltzmann新变量λ =xt-0.7269,使得满足浸润锋达到各测点时Boltzmann新变量为常量,但代入到Richard方程中不能化解为式(5a)的形式,发现采用文献[21]根据大量试验得到浸润锋位置和时间的关系如式(6)所示来拟合浸润锋位置和时间的关系,拟合得到c=1.343、d=-15.444,相关系数为0.999,据此构建的Boltzmann新变量λ*=(x -d) t-0.5能满足浸润锋达到各测点时Boltzmann新变量均相等且可化解得到类似(5a)形式的扩散度,只是将其中的λ变为λ*,具体推导过程如下:由λ*变换一维Richard方程左右端项,如式(7a)和(7b)所示,根据两者相等,并考虑到λ*-θ具有唯一关系,可由偏分转换为微分,可得式(7c),对式(7c)进一步积分,便可得式(7d),对式(7d)进一步化简便可得到D(θw),下文称该方法为改进方法,其所得结果和关系也绘于图8中,可见该方法可以较原有方法[11]得到更为统一的体积含水率和Boltzmann变量的关系。

在应用式(5b)求解扩散度时,随着含水率的增加,如图8所示Δλ/Δθ的绝对值先开始是增加的,然而在增湿到入渗试验终止前该值变小,此时出现随着含水率增大,D(θw)降低的不合理现象,文献[11]也出现该不合理现象。文献[11]采用的是固定时间、测不同位置含水率得到λ-θ关系,在近饱和区出现Δλ/Δθ的绝对值下降的现象,本文认为其原因在于如前所述入渗端面存在长度很小的饱和度接近100%的区域[17-18],在此区域含水率的突然再次增加,导致了Δλ/Δθ的绝对值随着含水率增加而减少;对于本文中出现该现象的原因为入渗后期,浸润锋通过了底端,使得整个试样含水率在最后阶段出现了含水率增加速率加大的现象,数据处理时当仅选取浸润锋入渗到底端之前的数据,便不会出现该现象。扩散度获得后,根据扩散度和渗透系数的关系,应用式(8)计算渗透系数,获得的渗透系数随吸力的变化如图9所示,对渗透系数函数仍然应用VG模型拟合,拟合结果也绘于图中。

式中:ψ表示基质吸力代表的水头,容水度dθw/dψ可用VG模型推得

图8 Boltzmann变量和体积含水率的关系

图9 根据Boltzmann变换方法所得非饱和渗透系数
4 各方法的可靠性分析
为进一步分析各方法所得非饱和渗透系数的可靠性,采用求解Richard方程的Hydrus-1d软件对一维入渗试验进行了数值模拟,该软件采用迦辽金有限元法求解Richard方程。对两种间接方法,采用如表1所示的参数进行计算;对于浸润锋前进法、Boltzmann变换法、Boltzmann变换改进方法,采用如图6和图9所示渗透系数函数;对持水曲线参数,则采用θs、a和n确定的情况下,针对持水曲线测试点拟合出θr,拟合值分别为0.171、0.170和0.182,虽然该参数有较大的变化,但实测点与这些拟合的持水曲线均很接近。
图10给出了采用各方法所得参数时预测的浸润锋迁移距离随时间变化曲线与实测变化曲线的对比,可见非饱和渗透参数对结果的影响很大,采用浸润锋前进法和Boltzmann变换改进方法所得参数时较为准确,采用未改进Boltzmann方法和间接方法所得参数则偏离较大。另外也对入渗量随时间的变化进行了预测和实测的对比,结论与上述类似。
为进一步分析浸润锋前进法和Boltzmann变换法的可靠性以及提高瞬态剖面法的有效性,应用数值试验检验了浸润锋前进法和Boltzmann变换法采用的假定,针对瞬态剖面提出了合适的测点布置位置和布置间距并检验了效果。
针对浸润锋前进法所采用“迁移的水分剖面”平行向前移动的假定,应用数值试验获得了浸润锋达到不同位置时的水分分布剖面,如图11所示,为了较好对比水分剖面的差异,采用离浸润锋的距离作为横坐标。由数值模拟结果可见随着入渗距离的增加,浸润区水分剖面由陡逐渐变缓,水分剖面前端形状逐渐一致,此时浸润锋前进法所采用的假定才基本满足,对于本文试验,应用浸润锋前进法的假定可以得到浸润锋到达各测点时的水分剖面,图11也给出了到达15 cm和45 cm时的水分剖面图,从结果上看到达15 cm处的水分剖面与达到45 cm处的水分剖面在前端很接近,说明水分剖面到达15 cm后便接近于平行移动,也说明了浸润锋前进法在本文试验中的适用性。为进一步说明在入渗距离较浅时,浸润锋前进法所采用的假定不能得到满足,数值试验中在离入渗端面5、15和30 cm处布置观测点,获得了含水率和基质吸力随时间的变化,然后应用浸润锋前进法即式(2a)和式(2c)获得了不同吸力下的非饱和渗透系数,并与输入的非饱和渗透系数函数进行了对比,结果如图12所示,离入渗端面较近测点所得非饱和渗透系数明显偏离输入的渗透系数函数,特别是在刚增湿时,可见对此区域测点水分剖面平行移动的假定不能得到满足。

图10 应用各方法所得渗透参数预测浸润锋迁移距离随时间的变化与实测变化曲线的对比

图11 水分剖面分布随不同入渗距离的变化
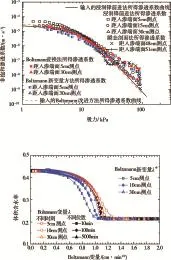
图12 数值试验中应用浸润锋前进法和瞬态剖面法所得非饱和土渗透系数与输入渗透系数函数的对比
针对Boltzmann变换法所采用Boltzmann变量与含水率关系唯一即Boltzmann变量仅是含水率的函数且为单值函数的假定,应用数值试验在离入渗端面5、10和30 cm处布置了观测点,根据不同时刻的含水率变化得到了λ-θ的关系;另外对于t=10 min、100 min和5000 min得到了土柱的水分分布,由此也得到了λ-θ的关系,结果对比如图13所示,可见应用两种方法,即定时间、变位置和定位置、变时间得到的λ-θ的关系,在入渗一定距离后(对应着入渗一定时间后)基本统一,与浸润锋前进法类似,在入渗距离较短时,也会出现一定的偏离。应用距入渗端面5 cm和30 cm测点所得λ-θ关系,计算得到的非饱和渗透系数如图12所示,可见应用距入渗端面5 cm测点所得渗透系数与输入的渗透系数函数偏离较大。另外按新的Boltzmann变量λ*也进行了分析,如图13所示,虽然提高了含水率开始增大时λ*的统一性,但增湿后的λ*-θ离散性增加,如图12所示,根据入渗距离较短时所得λ*-θ关系得到的非饱和渗透系数在高吸力区精度有所提高,但在低吸力区精度有所降低,而入渗距离较大时所得非饱和渗透系数,精度基本不变,由此可以推得室内试验采用新的Boltzmann变量能提高非饱和渗透系数精确度的原因在于考虑了试样的非均匀性和初始入渗边界条件并不严格满足的情况,而数值试验中均是均匀试样、初始入渗边界条件严格满足,变换其形式改善效果很小。

图13 数值试验中Boltzmann变量和体积含水率的关系
对于瞬态剖面法,为选择合适的测点位置和测点间距,根据水分分布剖面随入渗距离的增加从初始含水率到接近饱和的区段长度逐渐增加如图11所示,建议水分仪尽量布置在离入渗端面较远处,以使得瞬态剖面法布置间距可以适当增加,提高室内试验可操作性和减少传感器对试样均匀性的干扰。根据水分剖面形状较为稳定时含水率从初始含水率到接近饱和区段长度约为15 cm,建议在该长度内布置4~5个测点,则此时测点的间距为3~5 cm。为检验建议的测点布置位置和间距的有效性,数值试验中在距离入渗端面45 cm开始布置5个间距为3 cm测点,由数值试验所得结果按瞬态剖面法计算公式[7]所得非饱和渗透系数如图12所示,可见其在输入非饱和渗透系数曲线(浸润锋前进法所得)附近上下波动,这与文献[10]所得结果类似,其精度比室内试验瞬态剖面法有了较大提高,但精度仍不如浸润锋前进法和Boltzmann方法。需要说明的是,重塑黄土在入渗一定距离后便具有稳定的水分迁移剖面,而对于其他土类如膨润土,其在入渗过程中没有稳定的水分迁移剖面时,如文献[4]中的试验,浸润锋前进法和Boltzmann方法所采用的假定便不成立,此时只能应用瞬态剖面法。
5 结论
本文详细描述了确定非饱和黄土渗透系数的一维水平入渗试验测试系统和试验过程,主要比较了三种直接确定非饱和渗透系数的方法,并对其进行了改进,主要结论如下:
(1)对于浸润锋前进法,应用布置多个水分仪测点的方法可以代替原有通过观测的方法来获得浸润锋迁移速率;提出的水力梯度计算新方法可减少所得非饱和渗透系数的波动性;浸润锋前进法存在一定的假定,测点布置在离入渗端面较近处,所得非饱和渗透系数会有较大的误差。
(2)对于Boltzmann变换法,提出了Boltzmann新变量,减少了试样不均匀性和初始入渗条件不能严格满足的影响,其与含水率的关系较为统一。数值试验表明应用新变量所得非饱和渗透系数能更好预测浸润锋迁移距离和时间的关系;在入渗距离较短时,Boltzmann变量与体积含水率关系有所偏离,所得非饱和渗透系数精度较差。
(3)对于瞬态剖面法,由于本文试验中测点间距过大,所得结果具有较大误差,应用数值试验得到了浸润锋到接近饱和段长度随入渗距离的变化,由此确定了测试点合适的布置位置和间距,数值试验结果表明采用新的布置方案能够有效提高该方法的精度,但与前两种方法相比仍有较大的误差。
致谢:参加试验工作的还有谢瑞洪、罗梦秋、李博鹏和巴亚东,试验过程中李援农老师给予了指导。
