考虑球面波效应的水下爆炸冲击因子
2018-11-26陈祖煜魏迎奇张雪东梁建辉张紫涛
胡 晶,陈祖煜,魏迎奇,张雪东,梁建辉,张紫涛
(中国水利水电科学研究院 岩土工程研究所,北京 100048)
1 研究背景
重大水工结构是敌对势力和恐怖分子潜在的攻击目标[1]。在当量和爆距相同的条件下,水下爆炸对结构的破坏作用远大于空爆,其毁伤效应值得关注。然而,目前还缺少简单有效的指标评估水工结构在水下爆炸作用下的冲击环境,这限制了结构防护和设计理论的发展。
炸药水下爆炸后,冲击波呈球状向四周传播。通常,水下爆炸冲击波峰值由比例距离决定[2],因而早期北约和前苏联将比例距离作为指标考核潜艇以及舰船结构的生命力。研究表明:结构响应不仅与峰值压力有关,还与荷载作用的时间密切相关。对于远场水下爆炸作用,冲击波可以简化为平面波,目前各国舰船的防护规范中多采用平面波冲击因子[3],这一冲击因子也可以看作是冲击波峰值压力与冲量的乘积[4]。对于近场水下爆炸,除了爆炸冲击荷载和结构刚度等因素,结构响应还受自身几何特征影响,Yao等[5]基于能量遮挡率的概念,提出修正平面波冲击因子的方法,其可以考虑近场水下爆炸对水面舰艇的冲击作用。当爆距远大于结构尺寸时,该冲击因子与平面波冲击因子具有相同的形式。随后,Guo等[6]针对复杂船体结构验证了该冲击因子的适用性。然而,船体结构的宽度通常远小于长度,当爆距较远时,可以忽略能量沿船体宽度方向的变化。而对于高坝、船闸等水工结构,为了达到毁伤目的,爆距需远小于结构尺寸,忽略冲击波能量沿纵横方向的变化可能造成较大的误差,需要考虑水下爆炸的球面波效应。因而,有必要提出专门的指标评估水工结构在水下爆炸荷载作用下的冲击环境。此外,水下爆炸原型试验耗资巨大,而模型试验存在相似率的问题[7],目前水下爆炸研究往往借助理论和数值模拟开展,缺少必要的试验支撑。离心机通过施加离心力模拟重力效应,可以满足结构应力应变关系及水下爆炸荷载相似[8-11],是水下爆炸研究的有力工具,可以为冲击因子的验证提供试验方法。
为了简化分析,本文采用正面挡水、背面临空的平板结构作为研究对象,假定结构的变形、振动主要与作用于其上的能量相关,推导考虑球面波效应的冲击因子。采用数值模拟验证相同冲击因子条件下,平板应变能、动能的一致性。此外,结合离心水下爆炸试验成果,验证平板动力响应的峰值与球面波冲击因子的相关性。
2 冲击因子
2.1 典型冲击因子当荷载恒定或变化速率较慢时,通常可以忽略荷载的作用时间,由牛顿第二定律和胡克定律可知,物体的加速度、变形主要与荷载峰值有关。根据Cole理论[2],水下爆炸自由场的冲击波峰值主要受比例距离影响,因而早期学者采用比例距离作为衡量水下爆炸威力的冲击因子,其表达式如下:

式中:W为爆源当量;L为爆炸距离。
然而,大当量炸药在远距离处爆炸时,其时间常数远大于小当量作用,相应的冲量、能量均较大,会产生更严重的毁伤。对于冲击波,其能量密度可用下式描述:

式中,Es为能量密度;KE、αE为能量密度参数,与爆源种类有关,若忽略冲击波能量的衰减,指数αE=2。对于平面波,结构遮挡能量的面积S为定值,则可以根据作用于结构的能量定义平面波冲击因子,即:
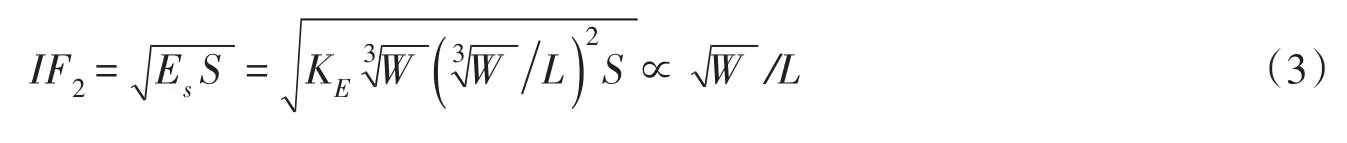
该冲击因子广泛应用于各国的舰船设计规范中。
2.2 球面波冲击因子推导由上述分析,可以认为结构动力响应与作用其上的能量相关。对于球面冲击波,距爆心相同半径处的能流密度相同,结构所受的冲击波能量可以通过其遮挡的球面积计算,而球面积计算则可以转化为结构边界与爆心组成的立体角(图1)。当爆源正对结构中心,爆源距平板中心距离为L,根据对称,取1/4结构进行分析,半板长和高分别为l、h。
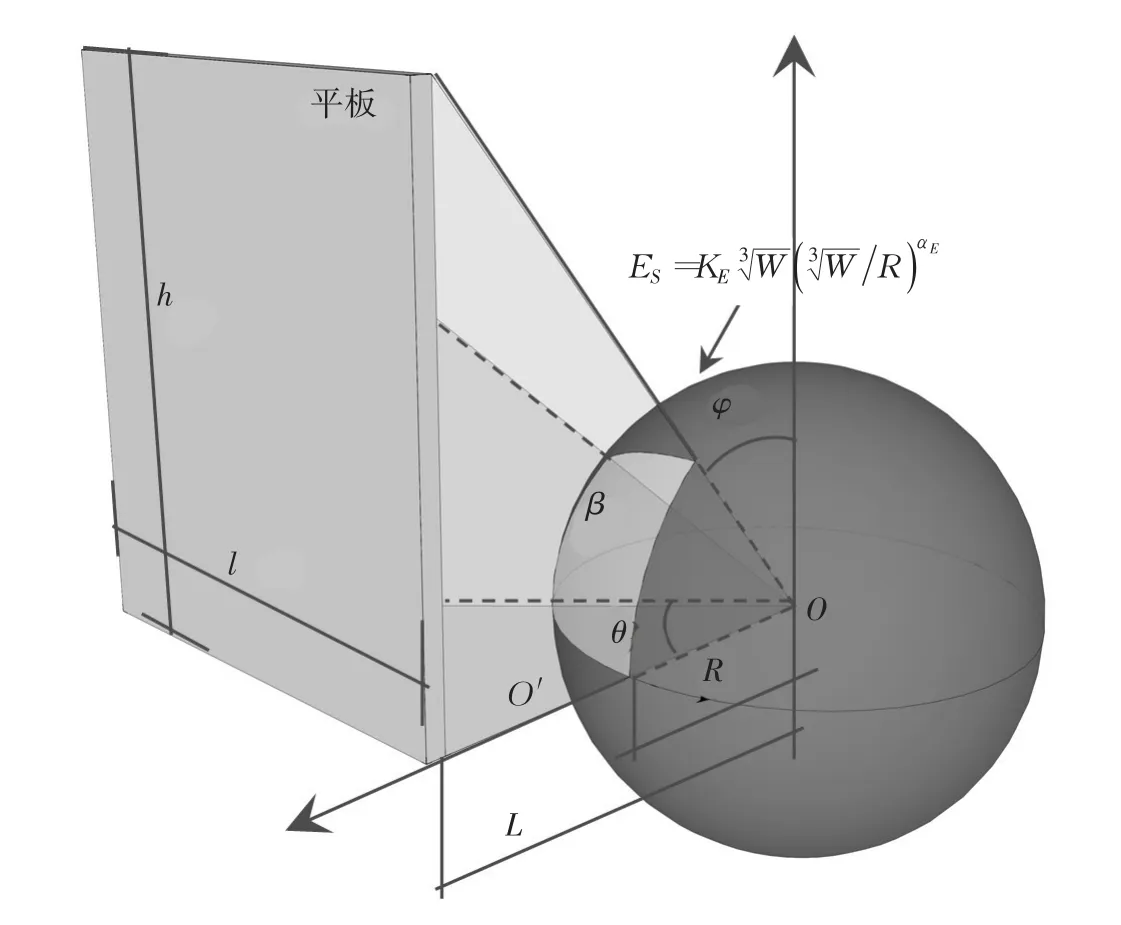
图1 平板受球面波作用示意图
以爆源为原点建立球坐标系,在平板表面选取面积微元,则其在半径为R的球面上投影为R2sinφdφdθ,φ、θ为方位角,则平板边界与爆心构成的立体角β可以通过如下积分进行计算:

其中:
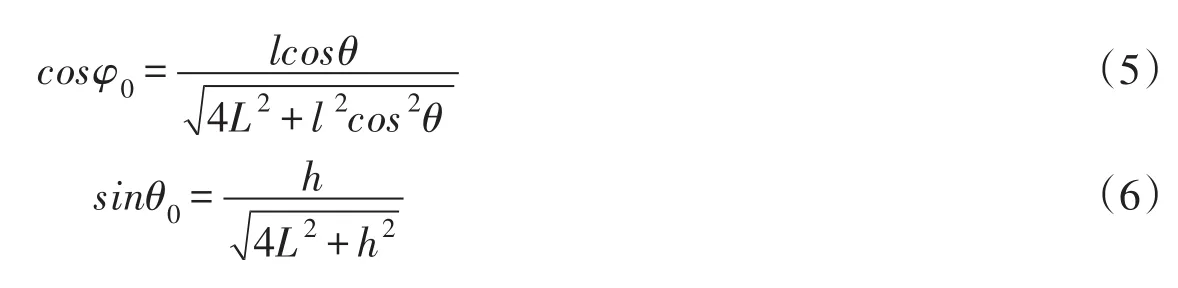
定义:

则:

其中:

结构遮挡的球面面积S=βL2,结合式(3)即可以构造出新的冲击因子,即:

式中,立体角β与爆源作用位置及结构几何尺寸有关,该冲击因子结合考虑了爆源当量、爆距、几何尺寸对结构所受冲击波的影响。
3 离心模型试验及数值模型
3.1 试验介绍为了试验验证冲击因子的有效性,基于文献[8]开展的离心模型试验进行研究。试验模型如图2所示,模型箱左侧采用砂浆固定5 cm厚的钢板,形成类似船闸的挡水结构。文献[8]详细介绍了离心模型试验的工况,验证了水下爆炸冲击波及气泡脉动的相似性,并初步探究了水下爆炸冲击波及气泡脉动共同作用模拟方法。本文将针对平板的峰值响应进行分析研究,评估冲击因子的有效性。表1给出了试验工况,其中L、R分别为爆源与钢板及传感器的距离,D为爆源水深。
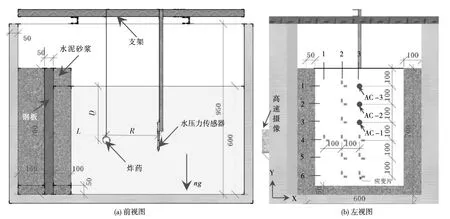
图2 试验模型[11](单位:mm)
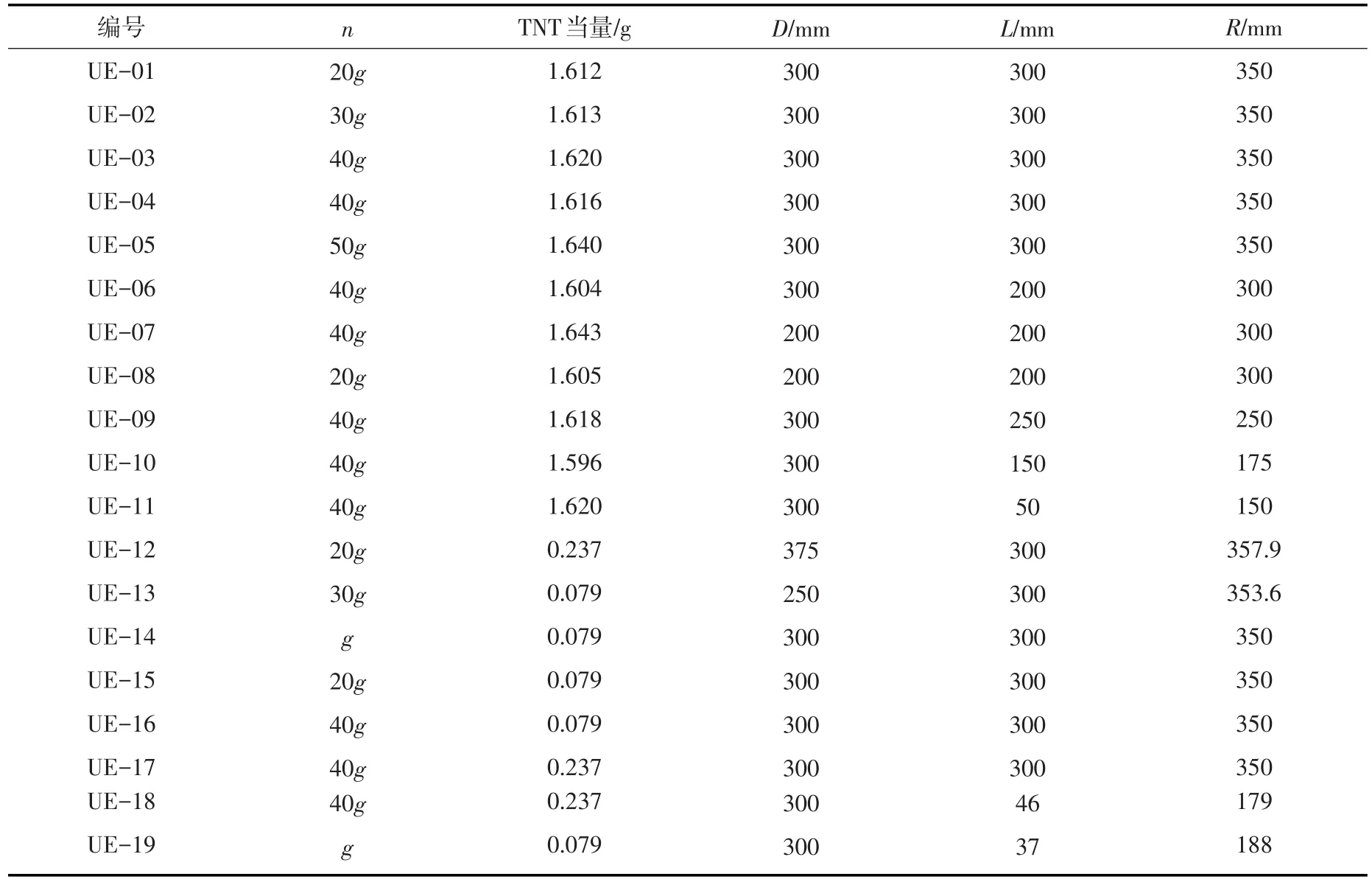
表1 试验工况
3.2 数值模拟对于水下爆炸冲击波,可以采用声学介质理论对其进行简化分析。若假设流动是无损且绝热的,忽略流体黏性效应并采用线性等熵状态方程,则声场可以采用唯一的变量压力p描述,Navier-Stocks方程可以简化为波动方程:

式中:p为压力;t为时间;ρw为流体密度;c为介质的声速;∇为梯度算子。为了考虑结构的动力效应,在静力平衡微分方程上引入惯性力项,即:

式中:ρs为结构密度;u为位移;σ为结构应力;fv为体力。
平板及水泥砂浆支座均采用弹性本构模型。假定结构湿表面的加速度法向分量与周围流体相同,则流固耦合控制方程为,即:

式中,n为结构湿表面法向量。
为了采用有限元方法对以上方程求解,建立如图3(a)所示的1/2数值模型,模型前表面为对称边界;由于箱壁为刚性,因而除了空气上表面,所有声学介质表面都按硬声场边界处理;砂浆、钢板的侧面、底面为固定边界;整个模型置于40 g的重力场下,g=9.8 m/s2;采用球面波辐射边界模拟冲击波作用,在流场指定位置设置半球形凹坑(re=1 cm),在半球边界施加指数衰减的球面波辐射,其压力时程曲线可以采用Cole公式描述:

式中:pm为峰值压力;θ为时间常数。
模型采用细化的渐变网格进行离散(图3(b)),其控制参数见表2,其中最大单元生长率限制两个相邻网格单元的尺寸之差,曲率因子决定弯曲边界附近单个网格单元的尺寸,狭窄区域解析度控制狭窄区域的网格单元层数。在水下爆炸作用下,冲击波能量将转化为平板的应变能和动能。
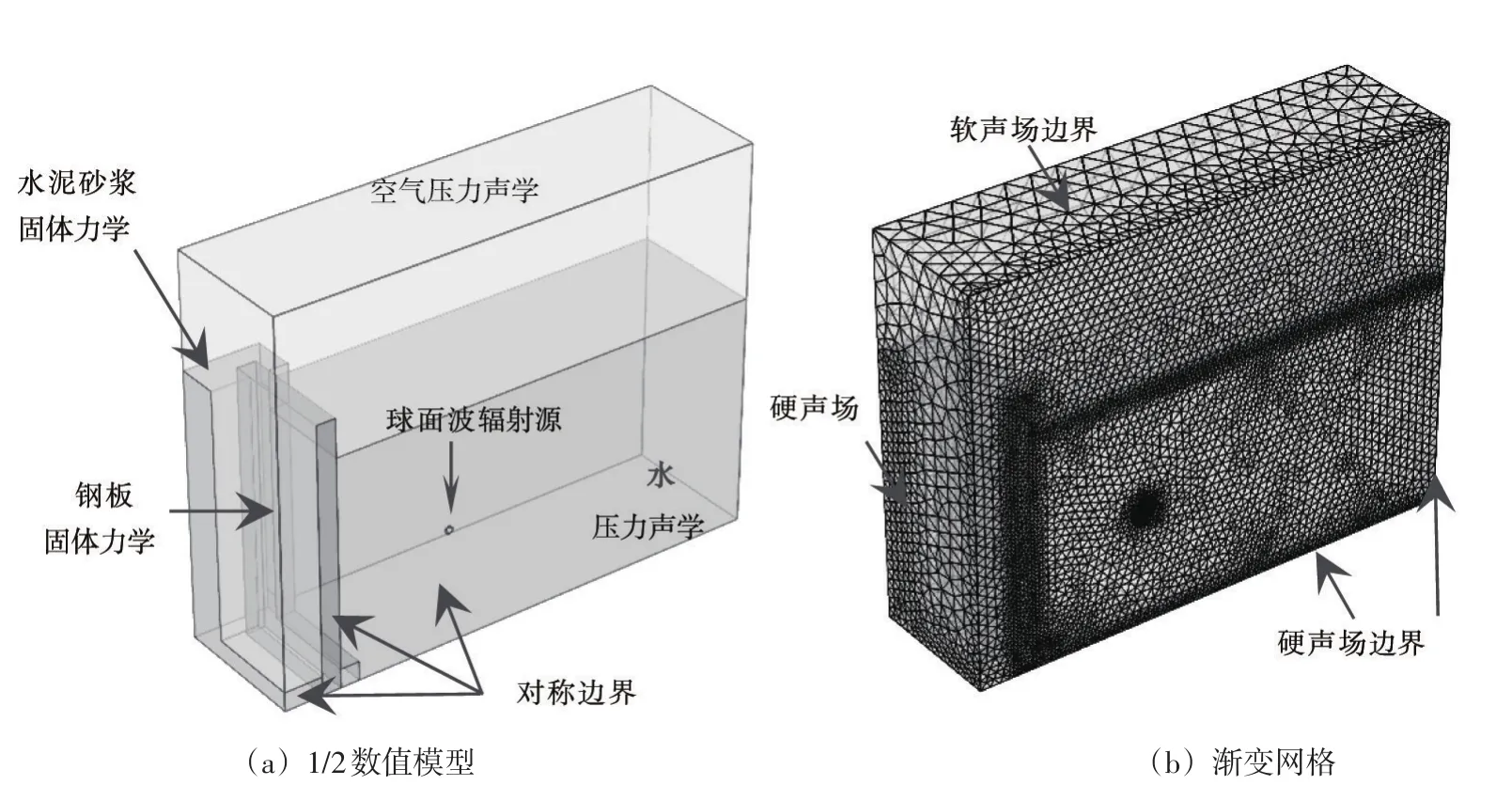
图3 数值模型

表2 网格划分控制参数(细化)
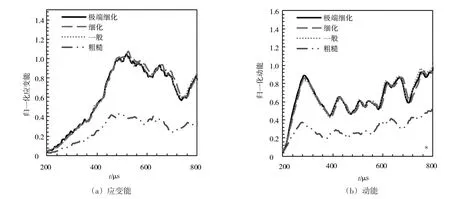
图4 网格敏感性分析
图4给出了不同离散程度下平板总的应变能和动能时程曲线,随着网格的细化,结构能量逐渐趋于收敛,本文采用细化的网格可以平衡计算精度和计算量。表3列出了数值模拟的工况,各个工况的冲击因子均保持相同,爆源当量和对应的峰值压力可采用下式计算:
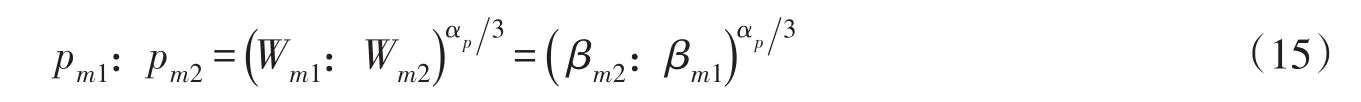
式中下标m1、m2为不同工况。
4 结果分析
4.1 冲击因子的数值验证为了验证本文选用参数(表3)的合理性,采用轴对称模型计算了水下爆炸冲击波的传播过程,图5为距爆源不同距离处的冲击波压力波形。由图5可见,数值模拟结果与试验基本一致,冲击波随距离、时间衰减规律与试验接近。图6给出了工况1所得的平板Mises应力云图及变形发展过程。由图6可见,爆炸200 μs后,冲击波到达结构表面,平板局部产生质点振动;随后平板在冲击波作用下产生弯曲,爆源正中变形最大,迎水面受压、背水面受拉;虽然冲击波持续时间只有100 μs左右,但是在爆炸能量及惯性作用下,变形仍持续发展,500 μs左右平板变形达到峰值后逐渐减小;由于结构为弹性,800 μs左右平板产生反向变形,板体不断振动。
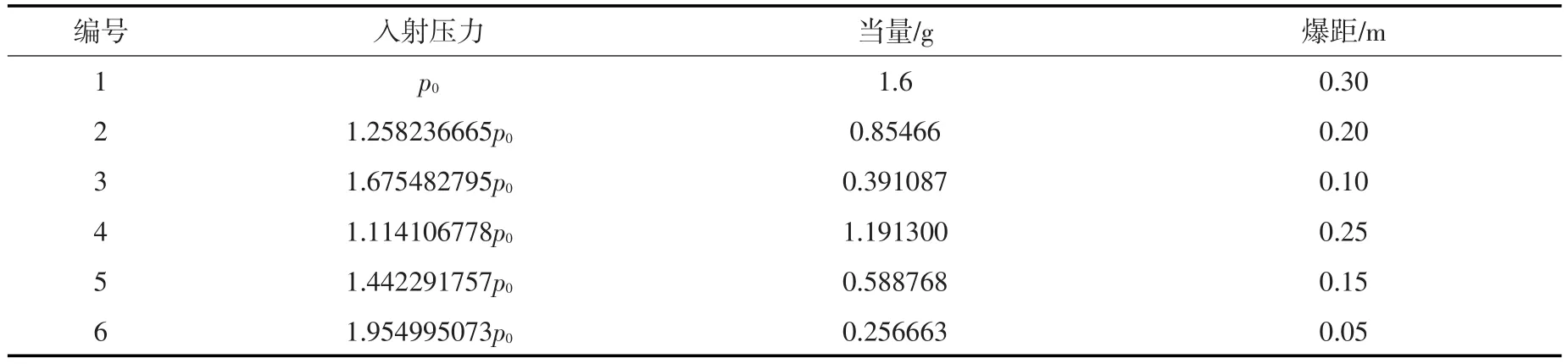
表3 数值模拟工况
式(10)所得的冲击因子综合考虑了爆炸当量、爆距、结构尺寸等因素对水下爆炸作用的影响。为了验证其有效性,在冲击因子相同的条件下,改变爆距进行了一系列模拟(表3),水下爆炸对结构产生的能量时程曲线如图7所示。各个工况应变能和动能的变化趋势相近,能量峰值几乎一致,各条曲线可以通过平移近似得到。模拟的结果证实该冲击因子可以合理反映结构的应变能、动能,而应变能和动能决定了平板的振动和变形。因而,本文所得的冲击因子可以综合考虑爆距和爆源当量的影响,用于评价结构所处的冲击环境。
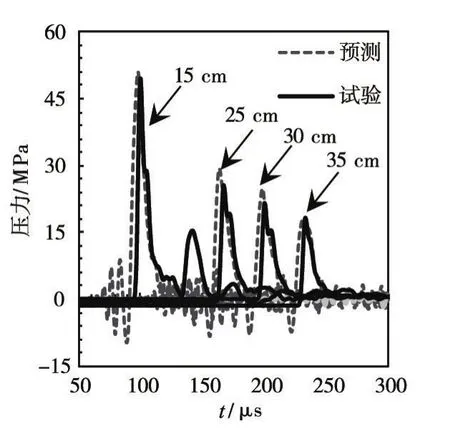
图5 不同距离冲击波时程曲线
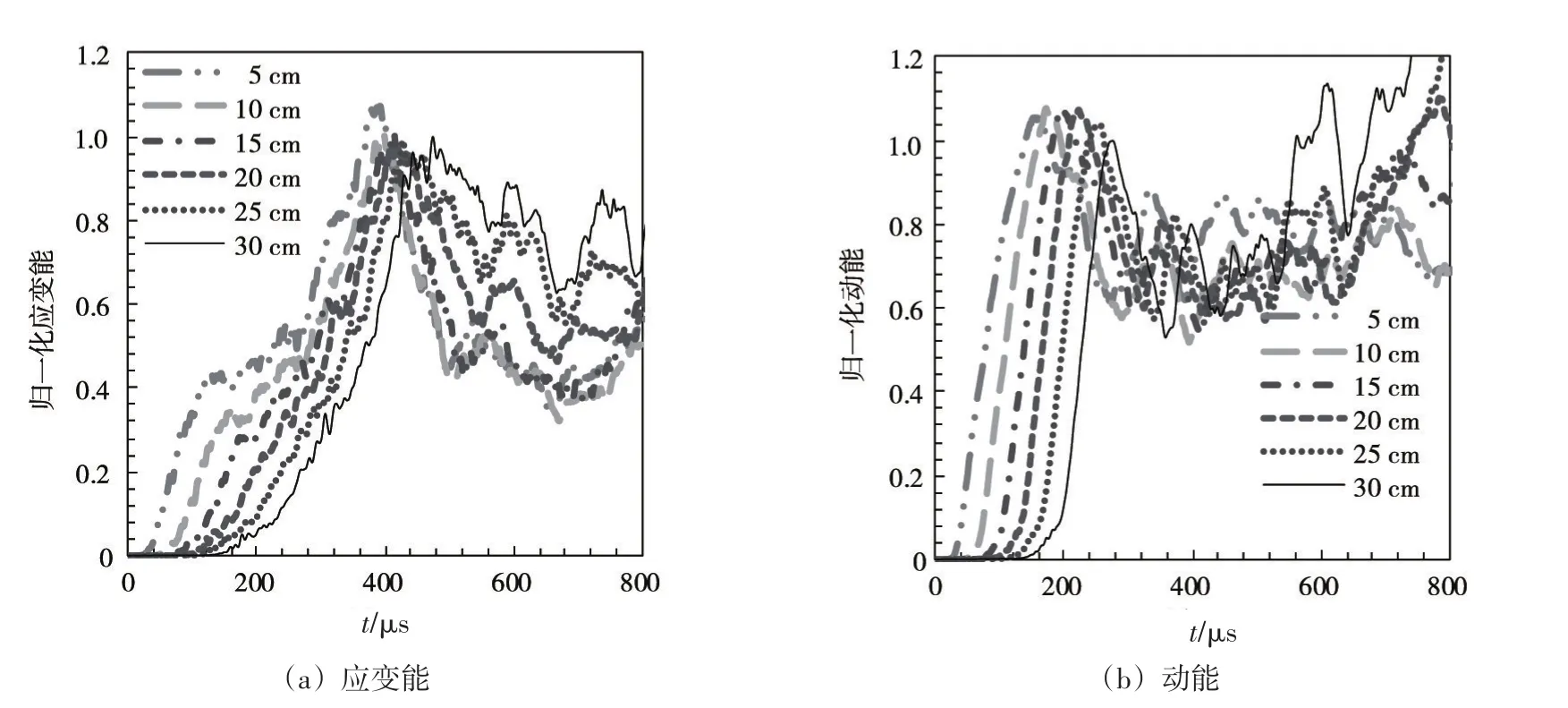
图7 不同爆距相同冲击因子作用下平板的能量
4.2 试验结果为了进一步检验冲击因子的有效性,本文结合离心模型试验得到的结构响应开展研究。图8为平板在水下爆炸荷载作用下的变形及振动响应,在冲击波和气泡脉动的联合作用下,时程曲线中包含多个峰值,首个峰值为冲击波作用。由于研究主要针对球面冲击波作用,因而整理出各个工况的首个峰值(表4)。
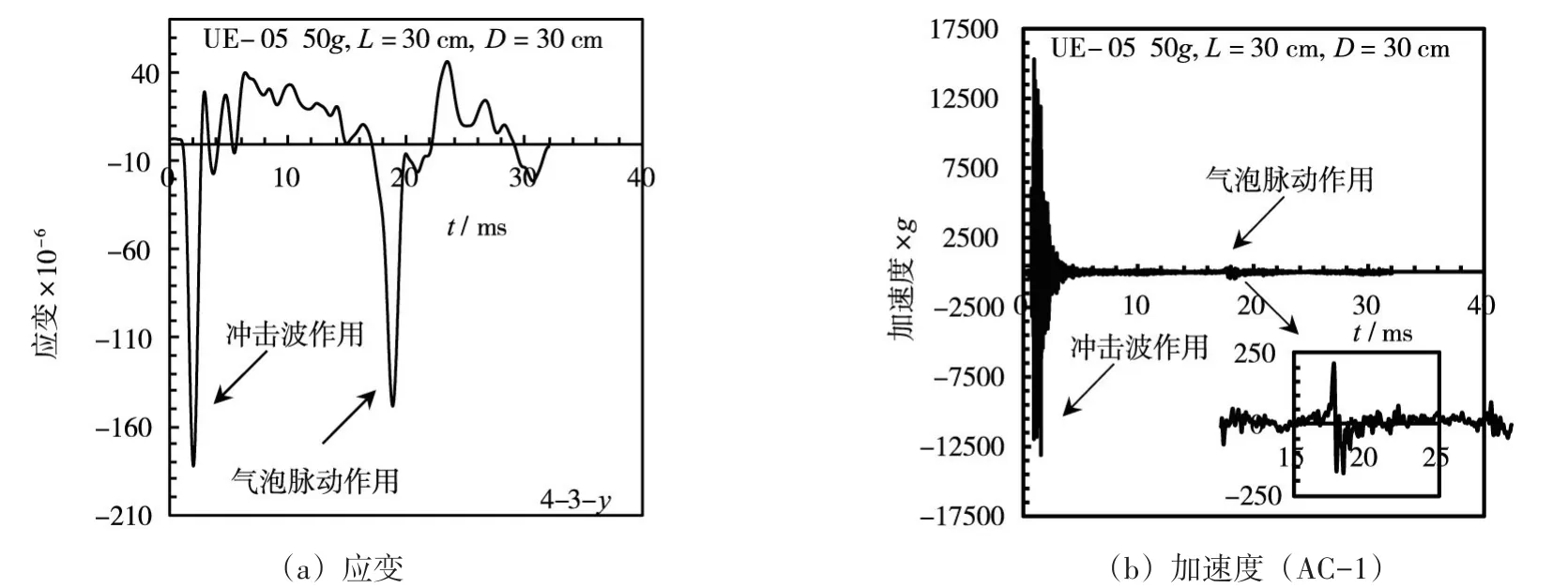
图8 相同冲击因子不同爆距作用下平板的能量
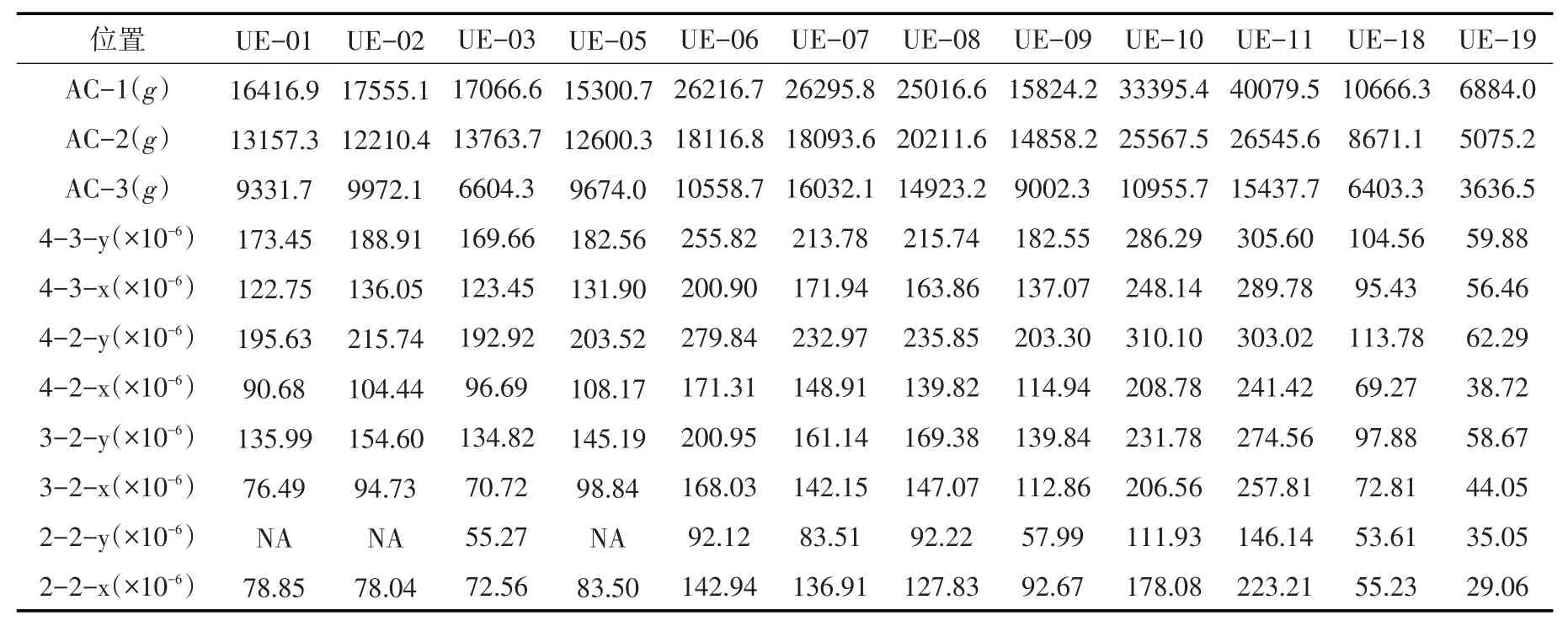
表4 各个工况不同测点首个峰值
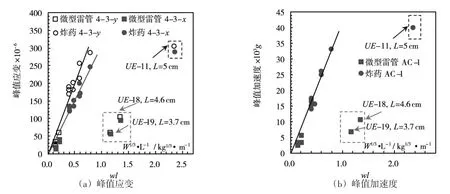
图9 比例距离拟合结果
采用比例距离和平面波冲击因子对试验数据进行整理分析,图9、图10给出了几个代表性测点加速度、应变峰值的拟合结果。当爆源与结构距离相对较远时,应变和加速度的峰值与比例距离或平面波冲击因子近似呈线性关系。然而对于UE-18、19,虽然峰值压力或冲击因子与其它工况相近,但是其当量较小,产生的响应值明显低于其他试验值。对于UE-11,由于作用距离较近,其响应值也明显低于趋势线。传统冲击因子难以统一描述不同当量炸药近场及远场作用下结构的动力响应。
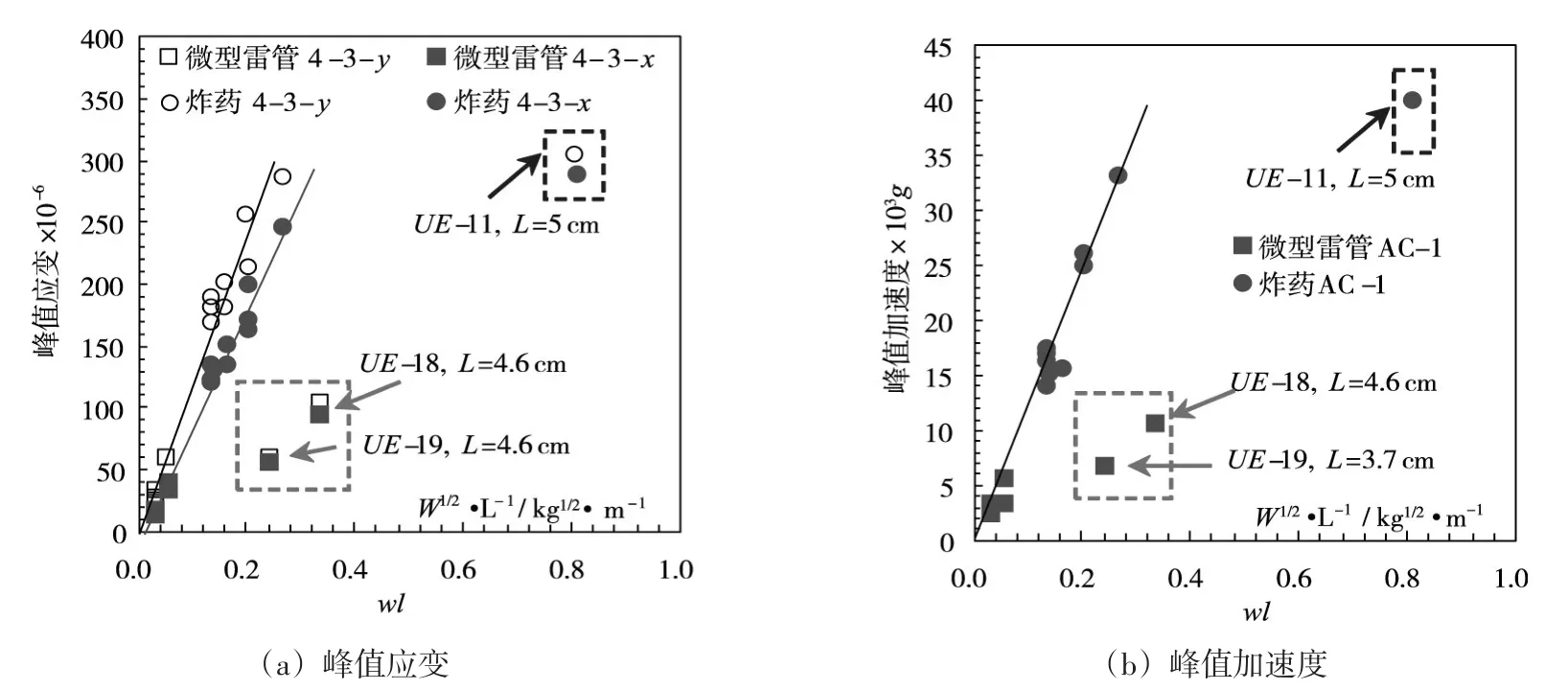
图10 平面波冲击因子拟合结果
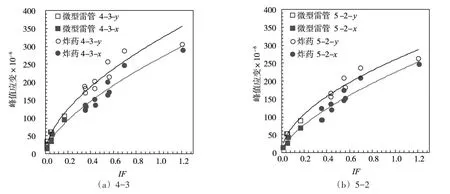
图11 峰值应变与冲击因子的关系
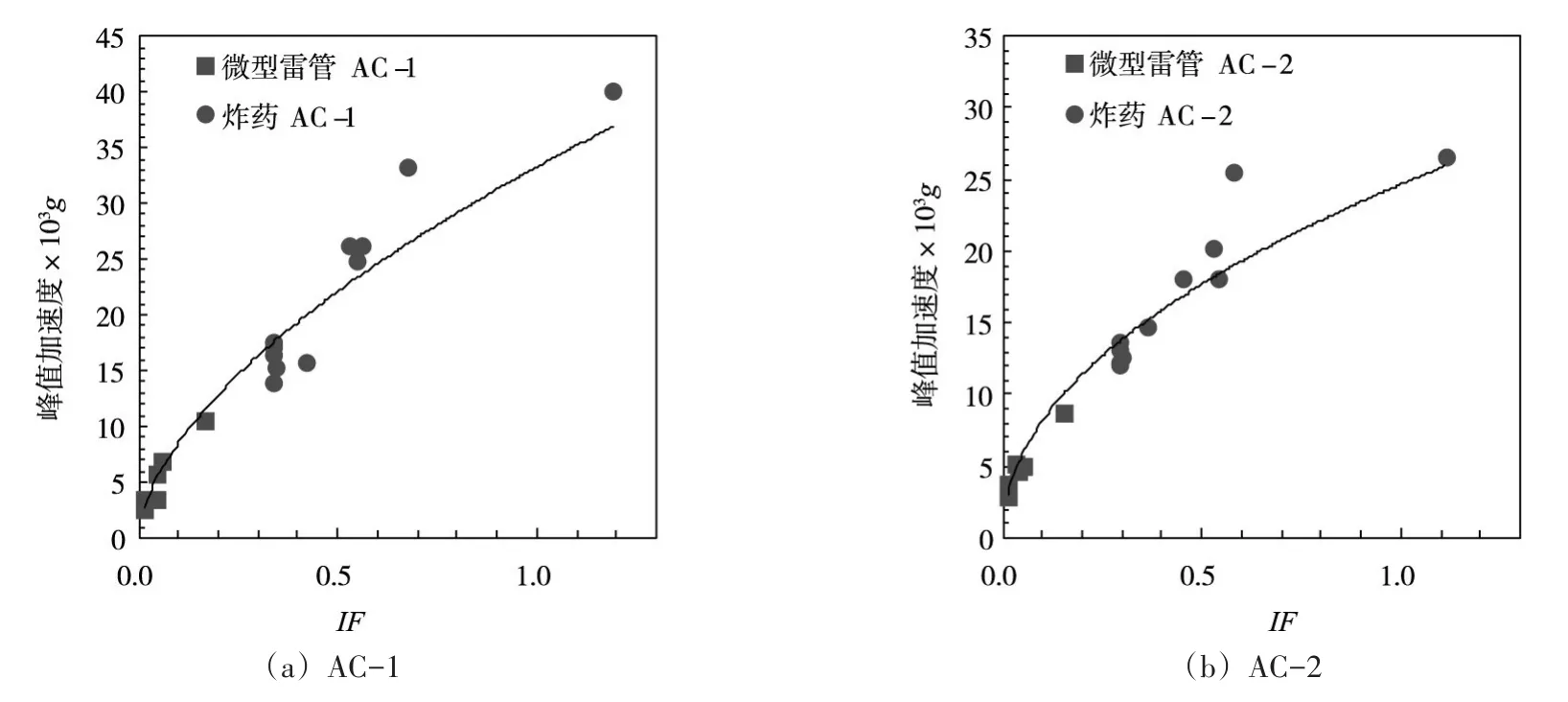
图12 峰值加速度与冲击因子的关系
进一步采用球面波冲击因子对试验结果进行整理分析(图11,图12),各个测点的试验数据与冲击因子表现出了较好的相关性,应变、加速度峰值与冲击因子近似呈幂函数关系,冲击因子越大,峰值响应同样越大,试验结果验证了本文冲击因子的有效性。
4 结论
本文提出了考虑球面波效应的冲击因子,并结合离心模型试验及数值模拟对其进行验证,得到以下主要结论:(1)结构的动力响应主要与作用于结构的能量大小有关,基于结构遮挡冲击波能量的概念,可以推导出球面波作用下平板的冲击因子;(2)数值模拟结果表明:当球面波冲击因子相同的条件下,爆距的变化几乎不影响结构产生的应变能及动能响应;(3)传统的比例距离及平面波冲击因子无法统一描述近场及远场爆炸试验规律,而考虑球面波效应得到的冲击因子可以合理反映不同当量的爆源近场及远场水下爆炸对平板结构产生的冲击能量,可以统一描述近场及远场水下爆炸作用规律。
