解决需求可拆分车辆路径问题的先聚类后路径方法

闵嘉宁，金 成，陆俐君

（1.无锡太湖学院，无锡 214064；2.南京大学 管理学院，南京 210093）

0 引言

需求可拆分车辆路径问题SDVRP（Split Delivery Vehicle Routing Problem）松弛了经典VRP中对每个客户只能访问一次的约束[2]。这种松弛使得一个客户的需求可以由多辆车送货，或由一辆车多次送货；也就是说，当车辆的剩余容量不足以为某个客户提供完整的送货需求时，车辆仍然可以向该客户提供与车辆剩余容量相等的送货，而客户的剩余需求可以由其他车辆（或此辆车的下一次）提供送货。这样可以充分利用车辆的容量，降低使用的车辆数、减少碳排放和行驶距离，进一步优化车辆路径问题。因此，SDVRP一经提出，迅速成为VRP的一个重要分支，受到越来越多的关注[2]。

国外关于算法的研究正式开始于1989年，Dror和Trudeau[1]提出了一种局部搜索算法，并验证了当客户点的送货需求较大时，SDVRP的解决方案明显优于VRP。Belenguer等[3]为SDVRP构建了多面体模型，基于切平面法设计了一种混合算法；他们解决了规模相对较小的问题，取得了良好的效果。Archetti等[4,5]提出了一种TSA算法和基于这个TSA的改进的三阶段算法。Chen等[6]首先通过节约算法得到初始解，然后通过拆分客户点的需求改进路径。Jin等[7]提出了带有效不等式的两阶段算法。Jin等[8]提出了基于列生成算法的SDVRP混合启发式算法。Tan[9]设计了蚁群算法，实例验证表明，随着点需求/车辆容量的比例增加，需求分解的优势也随之增大。Gulczynski等[10]提出限制最小拆分需求量，开发了一个端点混合整数算法、通过一种增强的记录到记录的旅行算法进行求解。Aleman等[11,12]提出了自适应记忆算法和变量邻域TSA算法，并验证了后者优于前者。Archetti等[13]提出了列生成的精确算法，先把问题域分割成较小的子域，然后在子域中优化路径，试图缩小精确算法和启发式算法获得的最优解的差距。Wilck IV等[14]开发了一种SDVRP求解的构造启发式算法，计算结果表明，在行驶距离和计算速度方面性能优于列生成方法和两阶段法。

国内研究开始的比较晚，但是近年来关注度逐年提高。2006年谢毅[15]设计了一个用于求解SDVRP问题的禁忌搜索算法（TSA）和一个遗传算法（GA），案例分析表明，TSA在最优解和时间消耗方面优于GA。侯立文[16]采用了具有改进转移概率的最大-最小蚂蚁系统，设计了求解过程和分割点选取规则。孟凡超等[17]研究了TSA来解决这个问题。谢秉磊等[18]提出了蚁群算法。刘旺盛等[19,20]提出了k-means聚类算法，并设计了两种不同的算法：一种是先分组后路径；另一种方法是先路径后分组，比较表明，先分组后路径的方法有更好的性能。马华伟[21]建立了多时间窗的SDVRP数学模型，设计了一种改进的蚁群算法求解问题。汪婷婷[22]提出了基于反应阈值和求解刺激值的SDVRP问题的蜜蜂群体优化模型。向婷等[23]提出了一种“分组而后路径”的聚类算法：根据最近原则分组，通过设定分割阈值来限制车辆的负载达到一定的范围，并且使用蚁群优化算法来安排路线。

本研究领域中使用的大多数算法是启发式和元启发式方法，为了找到最优解，需要多次迭代和结果比较而后取优，虽然可以获得较优的行驶距离，但是计算过程非常耗费时间。为了解决这个问题，本文提出了一个 “先聚类后路径”算法：首先，根据最近原则对客户点按距离进行聚类；然后，采用“推出”和“拉入”操作，通过对客户的需求拆分，调整每个聚类的负载需求，在没有迭代的情况下获得最佳的重量平衡的聚类组；最后，采用禁忌搜索方法对聚类组中的路径进行优化。这样，可以在较短的时间内获得近优解。该算法将在减少计算时间和获得较优的行驶距离方面更具实用价值。

1 数学模型

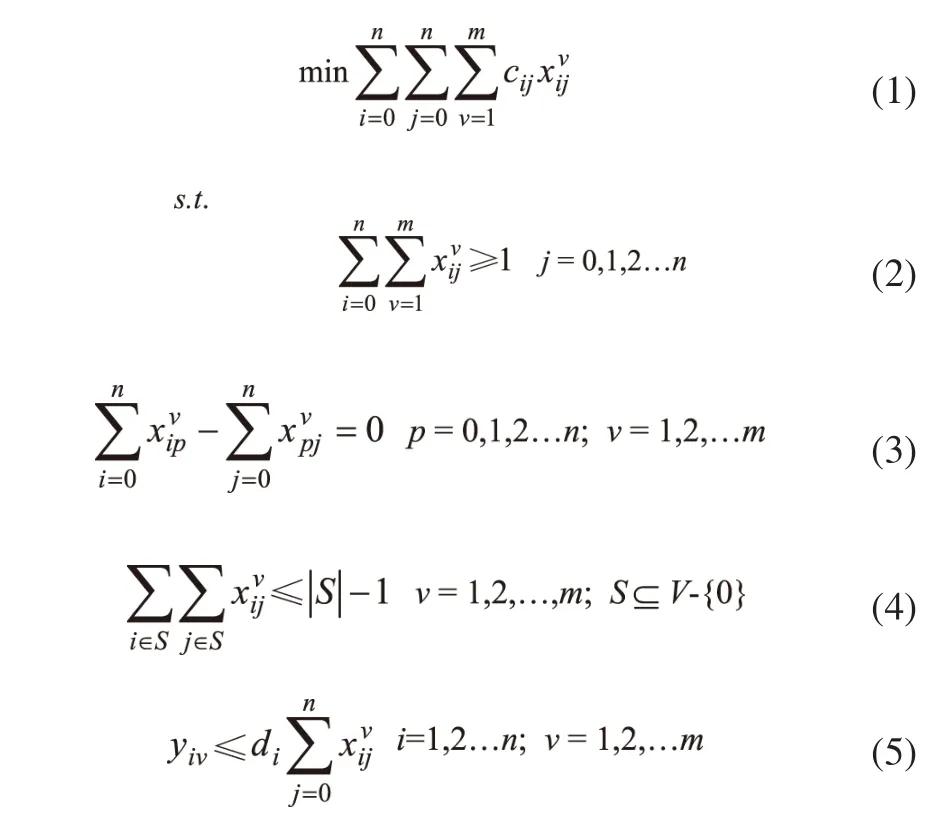
式(2)描述了每个客户点至少被访问一次；式(3)是流守恒约束；式(4)是子路径消除约束；式(5)描述了只有当车辆v访问客户i时，车辆v才服务客户i；式(6)保证了满足所有客户需求；式(7)保证每辆车不超载；式(8)描述了当车辆v从i直接到j时，=1；否则，=0；式(9)描述了yiv是车辆v为点i 送货的重量。

2 CRTS算法描述

该算法是一种基于先聚类后路径策略的三阶段算法CRTS（The Clustering first Routing later based Three Stage Algorithm）。第一阶段——对客户进行分组：根据其地理位置，采用最大最小距离聚类方法对客户点进行分组。第二阶段——调整每组的重量：采用“推出”和“拉入”操作，根据每个点的负载需求调整各组的重量，确定每个组的客户点。“推出”是将一个组的额外重量推给那些重量小于Q的邻组；“拉入”是从重量超过Q的邻组中提取重量到重量小于Q的组中。第三阶段——优化组内路径：采用搜索算法优化组内路径。该算法的具体过程如下。

2.1 前期处理

对负载需求di＞Q(i=1,2,…,n) 的客户点单独处理。di=Q的负载需求由一辆车进行送货，该点剩余的重量(di=di-Q)(i=1,2,…,n)以及其他的点di＜Q进入CRTS算法。

2.2 对客户分组

1）最大最小距离聚类算法的基本思想

最大最小距离聚类方法是一种模式识别方法。首先，按照最远距离原则，选择相距最远的点作为聚类中心，以提高初始数据集的分割效率[24]。然后，根据最近距离原则，将所有距离最近的点就近归入聚类组。

2）最大最小距离聚类的执行过程

Step1：令车场为x1作为第1聚类中心z1；

Step2：计算各点i(i =1,2,…,n) 到z1的距离Di1；

Step3：当Dk1=max{Di1}，选取xk作为第2聚类中心z2；

Step4：计算各点i(i=1,2,…,n)到z1和z2的距离Di1和Di2；

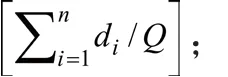
Step6：假如z3存在，计算Dl=max{min(Di1, Di2, Di3)}(i=1,2,…,n)，以及Dj＞θ*D12，选取xj作为第4聚类中心z4；以此类推，直至Dj≤θ*D12；

Step7：按照最小距离原则，划分所有的点构成组；终止运行。

2.3 调整各组的负载重量

客户点聚类分组后，计算并调整各组的负载重量。

1）“推出” 操作的执行过程

Step1：假如一个组的负载重量wg在 [α*Q, Q]之间，而且只有两个点，那么这两个点就形成一条路径，其中α大于负载率小于1；假如有µ1个这样的组，那么就有µ1条路径；

Step2：假如一个组的负载重量wg在[Q, 2*Q]之间，而且只有两个点，那么基于Q、这两个点就形成一条路径，剩余的负载wg-Q转入步骤4；假如有µ2个这样的组，就形成了µ2条路径；

2）“拉入” 操作的执行过程

Step1：按顺序访问负载重量wg＜Q的组（例如，组A）；

Step2：寻找距离A组中心点i最近的邻组点t（例如，组B中的点t）；

Step3：如果点t的负载重量dt＞(Q-wgA)且B组的负载重量wgB＞Q，拆分点t成为t1和t2，移动dt2=Q-wgA到组A，保留dt1=dt-(Q-wgA)；

Step4：如果点t的负载重量dt=(Q-wgA)且B组的负载重量wgB＞Q，移动(合并)点t(dt)进入组A；

Step5：如果点t的负载重量dt＜(Q-wgA)，首先，移动（合并）点t（dt）进入组A；如果B组的负载重量wgB＞Q，则在B组中搜索最近的点t'，让t＜-t'；如果wgB＜Q，则在另一个相邻的B'组中搜索最近的点t''，让t＜-t''；最后，进入步骤4；

Step6：如果A组的负载重量wgA为[α*Q, Q]，则结束对组A的处理；如果wgA＜ α*Q，则转到步骤2；

Step7：所有组访问完毕，则终止 “拉入”过程；否则，重复“拉入”过程。

2.4 优化组内路径

执行完“调整各组的负载重量”后，问题域被划分为几个较小的子问题域——聚类组，因此可以采用许多成熟的搜索算法来进行组内路径优化，获得最优解。本文采用禁忌搜索算法。限于篇幅，本文不讨论这个问题。

3 案例研究

为了验证CRTS算法的可行性和有效性，采用来自文献[7,19,23]的案例，并与采用先聚类后路径策略相应的算法TSVI[7]、k-means聚类方法[19]、拆分阈值的聚类方法[23]以及扫描算法[25]进行比较。实验是在Intel (R)核心处理器、8GB内存的Windows 7 64位机器上实现的。

3.1 案例组1

案例组1来自文献[7]。案例组1包含有三个实例(N7L1-N7L3)，各实例的客户数都是N=7，车辆最大载重量为1，车场坐标(0,0)；实例中客户点的位置以及各实例中22次执行 (Q1-Q22) 的送货需求分别见文献。

表1 CRTS与TSVI计算结果比较

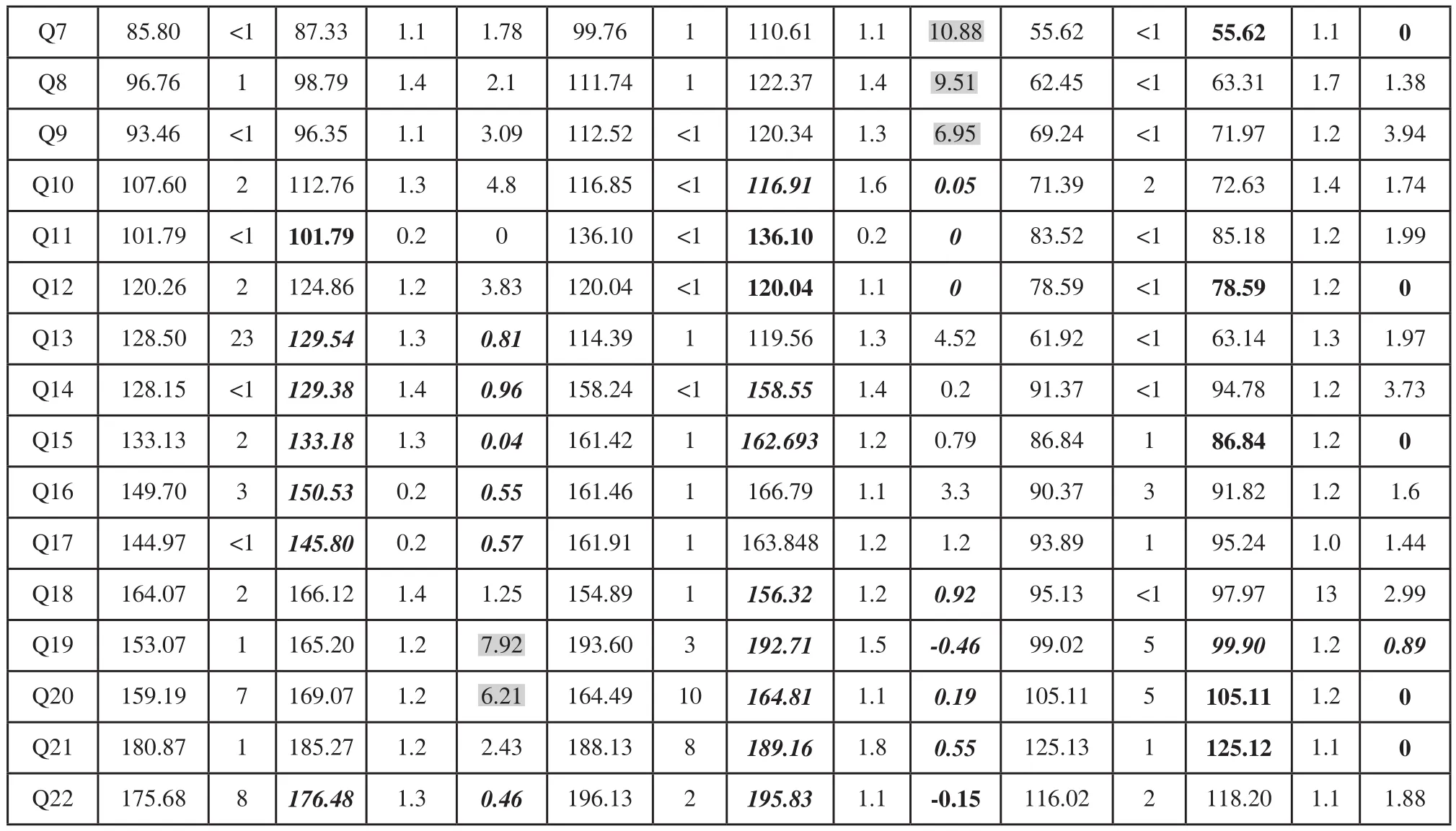
续（表1）

表1比较了TSVI和CRTS算法的总行驶距离(Distance)，计算所消耗的CPU时间s(T)，以及CRTS与TSVI总行驶距离相比较的相对偏差百分率RDP (Relative Deviation Percentage)：RDP=((DistanceCRTS-DistanceTSVI)/ DistanceTSVI)*100%。由于计算所消耗的CPU时间s很小，为节省显示空间，表1中计算时间(T)一栏表示的数字是CPU时间s的100倍。加粗字体表示其RDP≤0.0%，粗斜体表示其0.0%＜RDP＜1.0%，涂灰的数字表示其RDP＞5.0%。RDP≤0.0%和0.0%＜RDP＜1.0%的次数占总66次执行的46.97%；涂灰的数字占总66次执行的12.12%。

案例组1三个实例执行的总行驶距离结果如图1所示，两种不同算法曲线的吻合度很好，表明CRTS算法是可行的、有效的，尤其是计算所消耗的CPU时间s远低于TSVI。

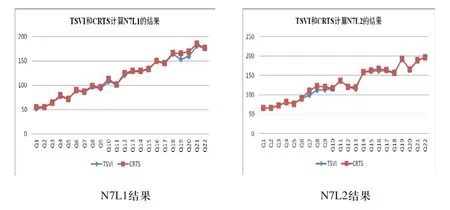
图1 案例组1三个实例的计算结果

3.2 案例组2

案例组2中四个实例来自文献[19,23]。各实例的客户数，客户总需求量，车辆最大装载量，所需车辆数如表2所示。各实例的客户位置、需求以及车场位置等基本信息见文献。

表2 案例组2各实例的基本信息

表3 CRTS与K-means聚类算法、拆分阈值聚类算法和扫描算法计算结果比较

图2 案例组2四个实例的执行结果

表3比较了K-means聚类算法、拆分阈值聚类算法、扫描算法以及CRTS的总行驶距离（Distance），计算所消耗的CPU时间(T)，以及CRTS分别与这些算法在总行驶距离和计算所消耗的CPU时间s比较的相对偏差百分率为RDP(Dis.)(RelativeDeviationPercentageforDistan ce)和RDP(T)，RDP(Dis.)=((DistanceCRTS–Distance某算法)/Distance某算法)*100%，RDP(Dis.)=((TimeCRTS–Time某算法)/Time某算法)*100%。表3中CRTS的计算结果采用了加粗字体。CRTS分别与前3种算法比较的RDP(Dis.)和RDP(T)的值都是百分率；正值表示CRTS的值大，负值表示CRTS的值小，凡负值涂有灰色。

表3显示：1）从总行驶距离来看，N=15、N=20和N=50三个实例中拆分阈值聚类算法最低，分别比CRTS低0.815%、4.067%和4.39%；N=36实例的CRTS最低，比拆分阈值聚类算法低0.805%；2）从计算所消耗的CPU时间s来看，CRTS最低，N=15、N=20、N=36和N=50实例分别比拆分阈值聚类算法低27.82%、30.37%、20.40%和58.51%。图2清晰表明：CRTS算法是可行的、有效的；图2(a)的曲线显示了N=20、N=36和N=50三个算例的总行驶距离的差别范围比较小，可以取得较好的总行驶距离；图2(b)显示CRTS的计算所消耗的CPU时间s远低于其他3种算法。

4 结论

本文介绍了SDVRP的数学模型，其目标函数是使用最低数量的车辆、通过安排合适的路线尽量减少总行驶距离。为了实现该目标，本文基于“先聚类后路径”方法提出了三阶段算法CRTS：第一阶段，采用最大最小距离聚类的方法对客户点域进行聚类，按照使用最小车辆数的原则将所有客户点分成子域，形成聚类组；第二阶段，采用“推出”和“拉入”操作，根据车辆最大负载重量Q值调整各组的负荷需求，获得重量平衡的聚类组；第三阶段，优化各组的路径，最小化总行程距离。两个案例组7个实例70次运行结果表明，CRTS算法为SDVRP提供了可行、有效的解决方案。该算法在总行驶距离的路径安排中可以取得较好的结果，尤其在计算时间方面，性能优于本文选用的TSVI算法、k-means聚类方法、拆分阈值聚类方法以及扫描算法等。