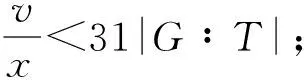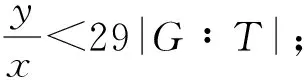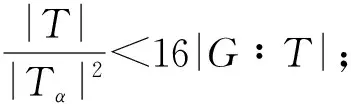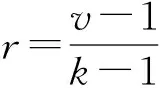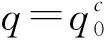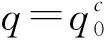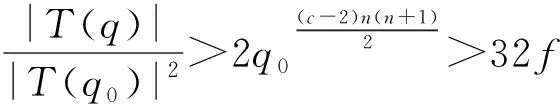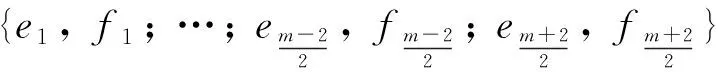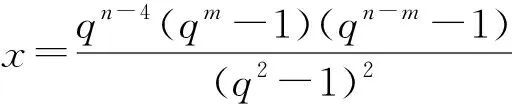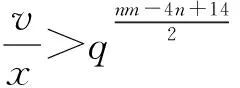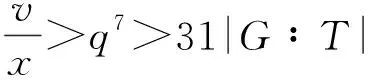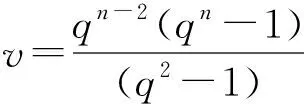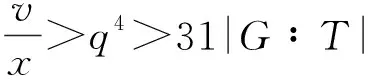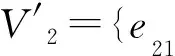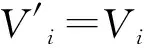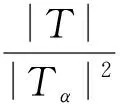区传递的2(v,6,1)设计与典型单群PSpn(q)

张彩红，韩广国，陈丽虹，张惠玲

(杭州电子科技大学 理学院 数学研究所， 浙江 杭州 310018)

0 引 言

设P为由v个元素组成的有限集(其中的元素称为点)，B为由P的k元子集组成的集合(其元素称为区)，2-(v,k,1) 设计D=(P,B) 是由P和B构成的二元系，满足P中任意2元子集恰好包含在唯一的区内.k满足2≤k

bk=vr，

bk(k-1)=v(v-1)，

且Fisher不等式b≥v[1]成立.

假设π是点集P的一个置换，若将D的区仍变为D的区，则称π是设计D的一个自同构. 记Aut(D)为D的全体自同构组成的群. 设G≤Aut(D)，若G作用在D的区集(点集)上是传递的，则称G是区传递(点传递)的. 若G作用在D的区集(点集)上是本原的，则称G是区本原(点本原)的. 称点区对(α,B) (α∈B)为设计D的旗. 若G在D的旗集合上传递，则称G是旗传递的. 已知结果： 若G是区传递的，则G也是点传递的[2]; 若G是旗传递的，则G是点本原的.

在研究具有良好传递性的2-(v,k,1)设计时，一个很重要的问题就是区传递2-(v,k,1)设计的分类.

目前，旗传递2-(v,k,1)设计的分类问题已基本解决. 对于可解的区传递2-(v,k,1)设计，已成功实现对3≤k≤9的分类[3-8]，针对自同构群为非可解群的情形，LI[9]对2-(v,4,1)设计进行了分类，HAN等[10]对2-(v,5,1)设计进行了成功分类. 经国内外学者的不断努力，区传递2-(v,k,1)设计的分类问题取得了丰富成果[3-19].

本文讨论非可解的区传递2-(v,6,1)设计，得到：

定理设D为2-(v,6,1)设计，其自同构群G≤Aut(D)是区传递、点本原但非旗传递的. 若v为奇数，则G的基柱Soc(G)不是有限域GF(q)上的典型单群PSpn(q).

1 预备知识

本文中的典型单群是指辛群PSpn(q). 记V为定义在有限域GF(q)上的n维向量空间，这里q=pf，p为素数. 因为PSp2(q)=PSL2(q)，该单群放在PSLn(q)中处理，故约定n≥4. 本文采用文献[20]的术语和符号.

引理1[17]设D是2-(v,k,1)设计，且G≤Aut(D)为区传递的. 若k|v，则G是旗传递的.

引理2[10]设G是点集P上的传递置换群，T≤G≤Aut(T)，记Γ为G的次轨道，则Γ为T的某些等长的次轨道的并.

引理4[14]设D为区传递的2-(v,k,1)设计，D的自同构群G是几乎单群，且G的基柱T为李型单群，若T∩Gα为T的抛物子群，则G是旗传递的.

2 定理的证明

设D,G满足定理条件，以下用反证法证明定理. 设G的基柱Soc(G)为典型单群PSpn(q). 方-李参数的定义[16]如下：

kv=(k,v)，kr=(k,r)=(k,v-1)，

bv=(b,v)，br=(b,r)=(b,v-1).

文献[16]证明了以下不等式：

k=kvkr，b=bvbr，v=kvbv，r=krbr.

接下来证明设计D的一些性质，该性质在下文的证明中将起到至关重要的作用.

命题1设D,G满足定理条件，且Tα=T∩Gα(α∈P)，则以下性质成立：

性质1v=1+30br或v=1+10br；

性质5若(v-1,q)=1，则Tα具有非平凡轨道Γ，其长度y满足y||Tα|P′.

k(k-1)b=v(v-1)，

再利用方-李参数，可得

kr(k-1)br=v-1，

所以有

v=1+kr(k-1)br.

因为G是非旗传递的，根据Camina-Gagen定理[17]可得6|/v，故kv=1或2或3. 又因为(kr,kv)=1且k=krkv，所以kr分别为6或3或2.

当kv=1时，v=1+30br，v为奇数；当kv=2时，v为偶数，与定理条件不符；当kv=3时，代入可得v=1+10br，v为奇数.

综上，v=1+30br或v=1+10br.

性质2的证明假设Γ1是T的任意一个非平凡次轨道，Γ是G的包含Γ1的次轨道，x与λ分别表示Γ1和Γ的长度，由引理2可知λ≤x|GG∶T|，又由文献[9]引理2.1可得br|λ，所以br≤λ≤x|G∶T|.

当v=1+30br时，若br>1，有

若br=1，因为Γ1是T的非平凡次轨道，所以有br<λ≤x|G∶T|，从而有

其余类似证明.

性质3的证明设Δ1和Δ2是T的任意2个非平凡次轨道，Γ1和Γ2为G的2个非平凡次轨道，且Δ1⊆Γ1(α∈P)，令x，y，λ1和λ2分别表示Δ1，Δ2，Γ1和Γ2的长度，则由引理 2可知

λ1=t1x，λ2=t2y，

这里t1，t2是|G∶T|的因子.

性质4的证明设B={1,2,…,6}为D的一个区，则子群GB的结构、群G的秩和次轨道的以下2种情形不成立：

GB的结构G的秩 次轨道

或

GB的结构G的秩 次轨道

否则，由文献[4]的结果可得G的阶为奇数(因GB的阶为奇数)，故G的最长次轨道的长度λ≥2br. 由引理 2可知性质4成立.

性质5的证明由文献[10]的结果可知性质5成立.

因为G为点本原，而且v=1+30br或v=1+10br为奇数，故G为奇数次本原群. 由奇数次本原群分类定理[21]得G的基柱H=Gα(α∈P)为下列情形之一：

(1) 若q为偶数，则H∩T是T的抛物子群.

若q为奇数，则下列(2)～(4)之一成立：

(3)H为V的非奇异子空间的稳定化子.

(4)T∩H为V的直和分解V=⊕Vi的稳定化子，其中Vi相互等距，且dim(Vi)是一常数.

接下来，将情形(1)～(4)一一排除.

命题1情形(1)不成立.

证明若H∩T为T的抛物子群，则Gα∩T也是T的抛物子群，由引理 4知G是旗传递的，与已知条件矛盾.

命题2情形(2)不成立.

与性质4矛盾.

命题3情形(3)不成立.

证明设H为V的任意非奇异子空间的稳定化子，T=PSpn(q).

其稳定化子分别为Tα和Tβ，故

这里A1∈Spm-2(q),A2,A3∈Sp2(q),A4∈Spn-m-2(q),从而v和x(x为β所在Tα的轨道长度)分别为

故

(1)

命题4情形(4)不成立.

当m=2k≥4时，设Vi的一组基为{ei1,fi1; …;eik,fik}(i=1,2,…,t)，取

由命题1～命题4，定理证毕.