基于模糊邻近支持向量机的伴随保障携行器材决策研究∗

朱 臣 罗广旭 余 震

（1.空军勤务学院航材四站系 徐州 221000）（2.空军装备部外场局 北京 100000）

1 引言

在军事斗争准备不断深入的今天，充当“拳头力量”的应急作战部队执行各类转场任务已经趋于常态化，而伴随保障作为转场训练中最直接的器材保障方式［1］，其水平的高低将在很大程度上影响转场任务完成的圆满与否。由于器材种类繁多，伴随保障所能携带器材有限，因此对伴随保障而言，携行器材种类的确定成了至关重要的问题。由于影响携行器材种类的因素很多且互相关联，同时许多因素具有不确定性即模糊性。本文运用模糊理论和邻近支持向量机相结合的综合决策方法，为伴随保障携行器材的确定提供参考。

2 理论基础

2.1 模糊理论

模糊理论是将无法量化、不具有确定性的数据转变成可量化的数值的一种数据处理方法。在指标体系决策指标体系中，可以运用模糊理论将定性指标去模糊化，即将定性指标量化，用具体数值来描述。

可用模糊语义描述定性指标为“很低、低、中等、高、很高”这五个等级，对各个指标进行反模糊化处理。模糊集的系数可由式（1）转化而得

对各等级的模糊隶属度函数如图1所示。

以模糊语义描述“中等”为例，求其指标系数，由图2可知a0=4，b0=8，a1=b1=6，c=0，d=1，代入式（1）有K(x)=0.583，同样其他等级对应的指标系数也可求得，如表1所示。

表1 反模糊化系数

2.2 邻近支持向量机

支持向量机（Support Vector Machine，SVM）是由 Vapnik［2～3］提出的一种基于统计学习理论的模式识别方法，是在VC维理论和结构风险最小化原则基础上发展出来的一种新的机器学习方法［4］，因而在许多应用中表现出很好的泛化性，既能有效地处理非线性数据，又能限制过学习，特别适合于小样本集的数据处理［5］。

而临近支持向量机（Proximal Support Vector Machine，PSVM）是由 Fung和 Mangasarian［6］提出的一种变形SVM，该算法的思想是在每类样本集的聚类中心设置与样本点临近的两个平行超平面，使得两个超平面之间距离最大（如图2所示），其约束条件也由标准SVM的不等式约束变成了等式约束［7］。

假设A是一个m×n数据矩阵，e是全为1的m×1列向量，y是m×1误差向量。D是m×n对角阵，其元素为+1或-1（+1表示样本属于A+，-1表示样本属于A-），ν是决定边缘和误差相对重要性的参数［8］。

满足约束 D(Aw-eγ)+y=e。

上述规划的拉格朗日函数为

其中u是拉格朗日乘子，据KKT（Karush-Kuhn-Tucker）得出充要优化条件为

将 w、γ、和 y代入公式 D(Aw-eγ)+y-e=0中，求解得到：

由此得到线性分类器平面：

而对于非线性分类器，将原变量w用其对偶等价w=ATDu替换，同时将线性核AAT替换为非线性核 K=K(A,AT)=K(φ(A),φ(A)T)［9］。

从而得到：

从而得到非线性分类器平面［10］：

综上所述，得到邻近支持向量机的分类规则为f(x)=sign((Ax+e)TDu)或sign((KK(A,x)+e)TDt)

3 基于模糊邻近支持向量机的伴随保障携行器材决策模型

3.1 建立评估指标体系

在开展飞行转场伴随保障中，携行器材的种类受到多方面影响，不仅涉及器材的使用寿命、发生故障的概率、维修的可行性，而且与任务的具体要求、人为因素以及外部环境等诸多因素都有着密不可分的联系。因此，针对携带器材种类的决策问题，在对伴随保障进行深入分析的基础上，综合考虑了当前影响航材保障工作各因素影响程度的差异，结合邻近支持向量机的决策原理选取了以下五个因素并做出了具体说明，旨在利用模糊邻近支持向量机在此类问题解决上的可行性与科学性给出更有利的说明［11～12］。

1）器材筹措性

由于伴随保障工作开展的前提是要在场站航材股进行器材的准备与领取，而器材的筹措往往会受到经费、储存空间等因素的限制，因此将器材筹措性作为决策因素之一，其具体的计算方法如下：

（计划库存数即在进行器材筹措时计划采购进行储备的数量）

2）器材故障性

伴随保障工作最主要的就是对可能出现故障的器材进行及时供应，因此，器材的故障性是必须考虑的决策因素。要定期对某一阶段器材的故障情况进行统计，得到各项器材在使用寿命内出现故障的数量（故障数），以及消耗的总数（消耗数），最终计算得到故障性：飞行目的地，还有一部分是直接放在飞机上，同飞机到达目的地。在运输中，需要考虑器材的大小和重量，保证在一定的运输空间和运输载重下，能尽可能多地运输所需器材，保障飞行任务顺利完成。器材运输性是定性指标，分为“很低、低、中等、高、很高”这个五个等级。

3）器材快速修复性

伴随保障携行器材在装机后，难免会出现一定的故障。所携带的器材数量有限，短时间内得不到相应补给，但又要保证飞行任务能够顺利完成，此时需要对损坏的器材短时间现场修复，所以器材快速修复的难易是需要考虑的决策因素。器材快速修复性是定性指标，分为“很低、低、中等、高、很高”这五个等级。

4）器材需求性

根据飞行任务，了解所需器材的功能，确定伴随保障所需携带器材相应种类。当同一种类有着不同型号器材时，就需要判定具体哪一型号的器材时更需要携带的。器材需求性是定性指标，分为“很低、低、中等、高、很高”这个五个等级。

5）器材运输性

伴随保障携行器材一部分是通过专门的地面运输通道（例如，汽车、火车等）提前到达飞机转场

3.2 计算流程

决策模型计算流程主要分为以下4个步骤：

Step 1：计算定量指标数值，利用模糊理论将定性指标去模糊化。

Step 2：通过Z-SCORE方法对数据进行规范化处理，得到规范化数据表。

Step 3：利用Matlab编程训练线性支持向量机，得到权重向量ω。

Step 4：每项器材数据的wTx-γ数值，其正负决定了器材的分类。

4 算例分析

某场站伴随保障携带器材的统计数据为训练样本（如表 2所示，“1”表示携带，“-1”表示未携带），如表1所示。

表2 某场站伴随保障携带器材统计数据

根据模糊隶属度函数对统计数据中定性指标去模糊化，结果如表3所示。

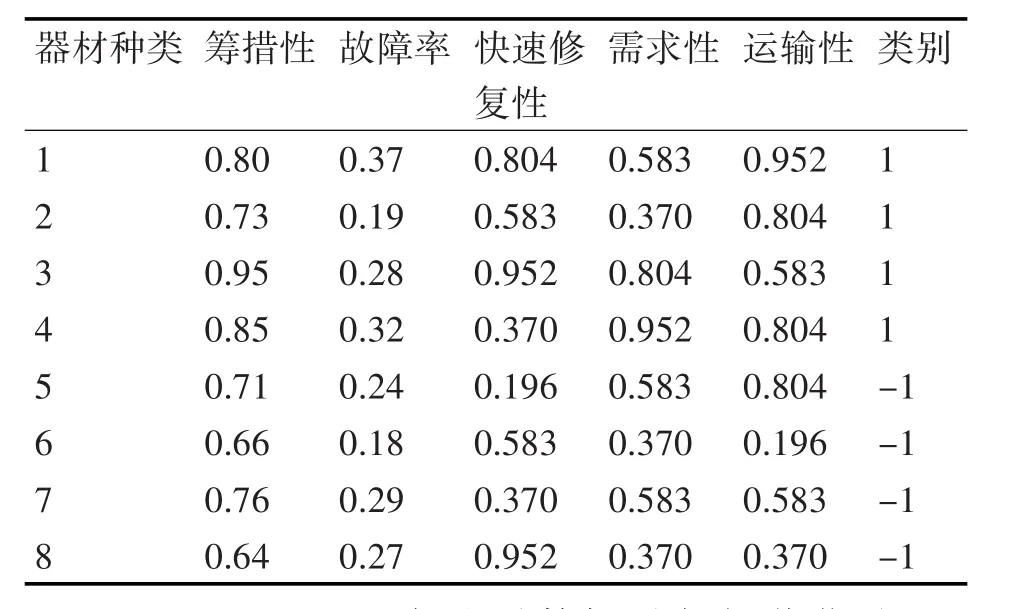
表3 去模糊化数据

通过Z-SCORE方法对数据进行规范化处理，如表4所示。

表4 规范化数据

利用Matlab编程训练线性支持向量机（取ν=0.1），得到权重向量为

如表5所示，得出每项器材数据的wTx-γ数值，其正负决定了器材的分类，结果中y（yes）表示决策正确，n（no）表示决策错误。

表5 数据的wT x-γ值及分类结果

通过以上实例的分析计算，得出了如表4所示的伴随保障器材携行种类的决策结果，从中可以看出，要携行器材1、3、4、7，不携行器材2、5、6、8。此线性核分类的正确率为75%，通过多次的训练，可以不断改进训练效果，从而提高分类决策的准确率。

同时，模糊邻近支持向量机通过对偶规划训练的传统思维，直接对原问题进行分析，在误差精度允许的范围内，大大加快了计算的速度。该方法在伴随保障携行航材种类中的应用可提高决策的精度与速度，确保航材保障现场供应工作的有效开展。

5 结语

在合理选取决策因素的基础上，利用模糊邻近支持向量机的分类决策方法，科学确定了伴随保障携行器材的种类。通过最后的实例，也验证了该方法在实际工作中携行器材种类决策的可行性，能够有效克服片面依靠主观经验所带来的弊端，提高航材保障人员开展伴随保障工作的科学性与针对性，明显提升航材保障的工作效率。