走进教材 追溯源头

范大阳

【教材重现】苏科版《数学》九年级上册第三章第一节“平均数”第二课时（99～100页）.

问题1：为了解某市九年级学生开展“综合与实践”活动的情况，抽样调查了该市200名九年级学生上学期参加“综合与实践”活动的天数，并根据调查所得的数据绘制条形统计图（图1）如下：

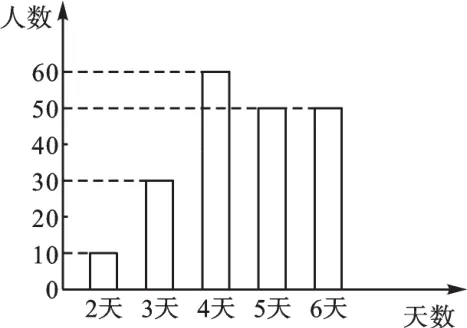
图1

求这200名学生参加“综合与实践”活动的平均天数.

小丽的算式为：

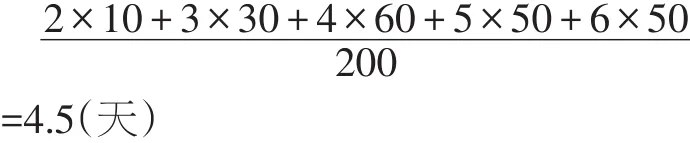
你认为上述两种算法哪一个正确？为什么？

这200名学生参加“综合与实践”活动的平均天数，不仅与参加活动的天数有关，还与相应的人数有关，因此小丽的算法是正确的.

这里的人数10，30，60，50，50分别是天数2，3，4，5，6的“权”.那什么叫做“权”呢？

一组数据的平均数，不仅与这组数据中各个数据的值有关，而且与各个数据的“重要程度”有关.我们把衡量各个数据“重要程度”的数值叫做“权”.这样算出来的平均数4.5就是数2，3，4，5，6的“加权平均数”.

由“问题1”而产生的变式问题在各地中考中极其常见，下面就让我们一起去探究吧.

例1为迎接“六一”儿童节的到来，某校学生参加献爱心捐款活动，随机抽取该校部分学生的捐款数进行统计分析，相应数据的统计图（图2）如下:

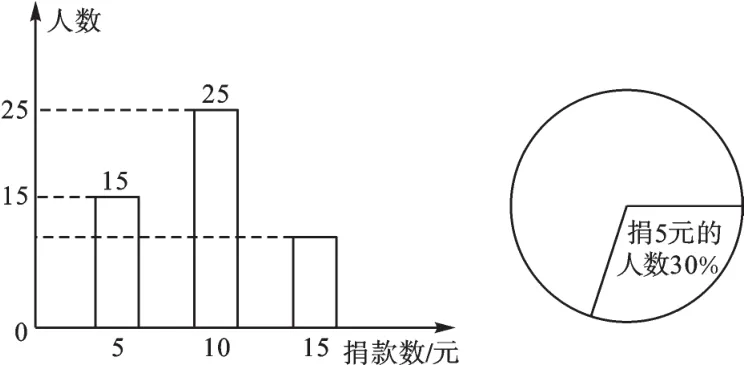
图2

（1）该样本的容量是_______，样本中捐款15元的学生有________人.

（2）若该校一共有500名学生，据此样本估计该校学生的捐款总数.

【解析】（1）50，10.

（2）样本中平均每人的捐款数为：

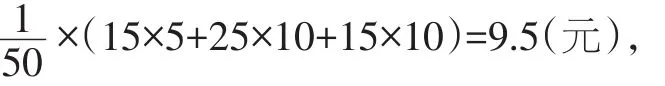
所以9.5×500=4750（元）.

这里的15，25，10分别是捐款数5，10，15的“权”，9.5就是5，10，15的“加权平均数”.

关于这种统计图的题目还有很多，下面我们再看一例.

例2为了解某种电动汽车的性能，对这种电动汽车进行了抽检，将一次充电后行驶的里程数分为A，B，C，D4个等级，其中相应等级的里程依次为200千米，210千米，220千米，230千米，获得如下不完整的统计图（图3）.

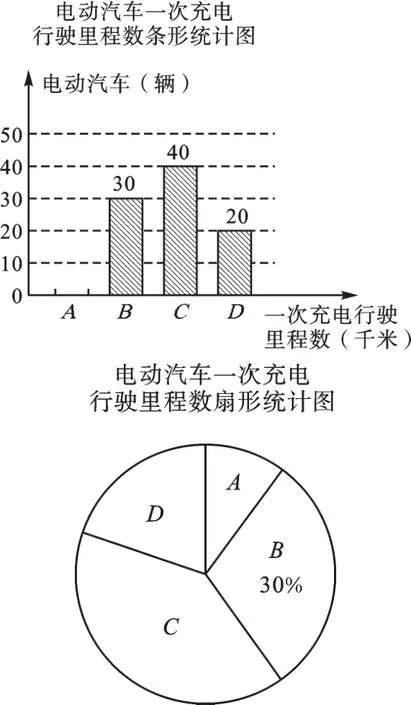
图3

根据以上信息，解答下列问题：

（1）问这次被抽检的电动汽车共有几辆？并补全条形统计图.

（2）估计这种电动汽车一次充电后行驶的平均里程数为多少千米？

本题考点：条形统计图、扇形统计图、加权平均数.

【解析】（1）具体过程略.共有100辆电动汽车被抽检，补全统计图如图（图4）所示：

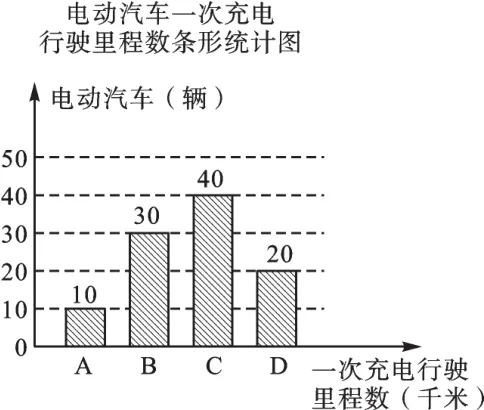
图4

这里的10，30，40，20分别是里程数200，210，220，230的“权”，217就是200，210，220，230的“加权平均数”.

【总结】看了这两道题目之后，不知同学们是否发现了规律.这类求平均数的问题，分母总是权数的和，分子是各个项目的权与代表该项目的具体数值的乘积的和.同学们，你们发现了吗？

当然，这类问题不止是以统计图的形式出现，还有以表格的形式出现，我们再看一例.

例3贵阳市“阳光小区”开展“节约用水，从我做起”的活动，一个月后，社区居委会从小区住户中抽取10个家庭与他们上月的用水量进行比较，统计出节水情况如下表：

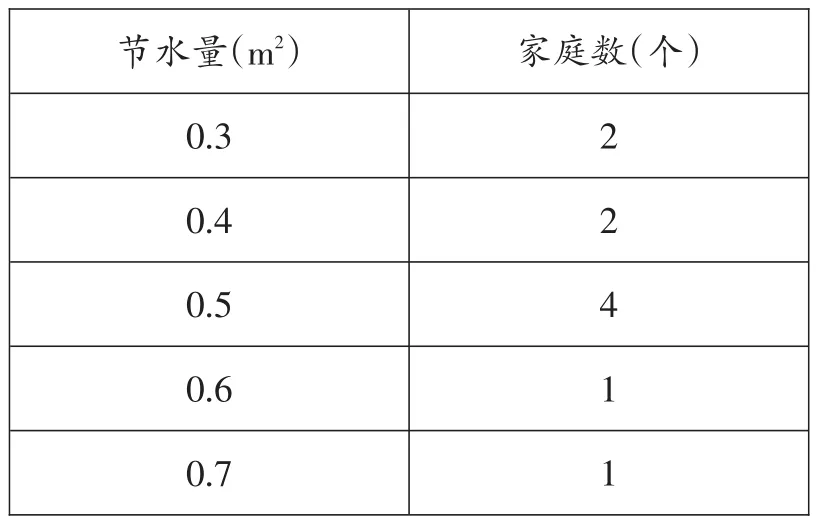
节水量（m2）0.3 0.4 0.5 0.6 0.7家庭数（个）2 2 4 1 1

那么这10个家庭的节水量（m2）的平均数和中位数分别是（ ）.

A.0.47和0.5 B.0.5和0.5

C.0.47和4 D.0.5和4

【解析】这10个数据的平均数为：

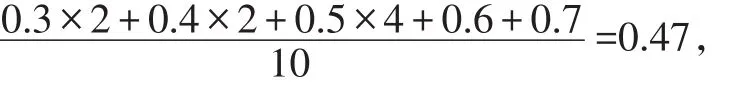
处于中间的两个数的平均数是0.5.故选：A.

这里的2，2，4，1，1分别是节水量0.3，0.4，0.5，0.6，0.7的“权”，0.47就是0.3，0.4，0.5，0.6，0.7的“加权平均数”.