A Novel Training Sequence Applied to DCS-Based Channel Estimation

Weizhang Xu＊, Xinle Yu Yanfei Li, Lu Si Zhanxin Yang Engineering Research Center of Digital Audio&Video Ministry of Education, Communication University of China, Beijing 0004, China

2 Communication Engineering Department, School of Information, Communication University of China, Beijing 100024, China

Abstract: Studies have indicated that the distributed compressed sensing based (DCS-based) channel estimation can decrease the length of the reference signals effectively. In block transmission, a unique word (UW) can be used as a cyclic prefix and reference signal.However, the DCS-based channel estimation requires diversity sequences instead of UW. In this paper, we proposed a novel method that employs a training sequence (TS) whose duration time is slightly longer than the maximum delay spread time. Based on proposed TS, the DCS approach perform perfectly in multipath channel estimation. Meanwhile, a cyclic prefix construct could be formed, which reduces the complexity of the frequency domain equalization (FDE) directly. Simulation results demonstrate that, by using the method of simultaneous orthogonal matching pursuit (SOMP), the required channel overhead has been reduced thanks to the proposed TS.

Keywords: jointly sparse channel estimation;distributed compressed sensing (DCS); simultaneous orthogonal matching pursuit (SOMP);training sequence (TS); unique word (UW);frequency domain equalization (FDE)

I. INTRODUCTION

Channel State Information (CSI) is an important element for the modern wireless communication. As a result, the data-aided channel estimation, which produces fewer errors and has a lower complexity, is widely adopted in today’s modern wireless systems. On the other hand, the conventional data-aided channel estimation methods only focus on the maximum delay spread, resulting an overutilization of bandwidth and energy. By examining the sparsity of the CSI of the broadband wireless system, one can find that the compressed sensing based (CS-based) channel estimation [1-2]is a parameterized estimation method. In other words, it estimates the delay and gain for each propagation path, respectively. It can offer more benefits to the channels such as fewer reference signals and better performance [3-5].

Multiple channel measurement instances are involved in the case of a broadband wireless channel estimation scenario, where the adjacent CSIs are dependent on each other. Such a setting is also known as the multiple measurement instances (MMI) in sparse parameter estimation. Studies have shown that compared to independent CS, MMI performance enhancement benefits from joint sparse approximation [6], such as simultaneous orthogonal matching pursuit (SOMP) [7]. There are two typical measurement matrices model for MMI,i.e. the multiple measurement vector (MMV)and the distributed CS (DCS). MMV assumes that all the measurement matrices are identical [6], whereas DCS assumes that different measurement instances use different matrices[7]. Empirical results have shown that the performance of DCS is superior to MMV [8]. In addition, Reference [8] reveals that it is the independent measurement matrices that actually optimizes the correlated signals.

The block transmission based on frequency domain equalization (FDE) is widely used,concerning the complexity and performance tradeoffs such as OFDM and SC-FDE [9].Guard interval is required to avoid the inter-block interfere (IBI), including cyclic prefix, training sequence (TS) and zero padding.Since the TS, usually consist of pseudorandom noise (PN) sequence, can act as guard interval and reference signal simultaneously, it is considered as the most promising method for single carrier systems. The frame structure of the block transmission system based on TS is shown in figure1. In a multipath propagation channel, the TS and the data block can cause the issue of mutual interferences. In order to avoid the interference, a method known as the double PN (DPN) can be adopted as the TS [10]. DPN improves the performance of channel estimation. However, the duration of each PN is still comparable to the maximum delay spread, which may cause more channel overhead. In order to improve the channel utilization, an iterative method is proposed in [11]. However, the CSI cannot be obtained immediately because of the slow convergence.As a result, losses become an inevitable issue in the fast fading channels.

Based on the foregoing discussion, one can conclude that TS appears in two forms:unique word (UW) and diversity sequence.On MMI-based channel estimation view, UW corresponds to identical measurement matrices, diversity sequence corresponds to different measurement matrices, which means that the estimation performance of the diversity sequence is better than UW. On FDE channel equalization view, conventional diversity sequence requires one to subtract the padding TS firstly before one performs the frequency equalization. Such a requirement is due to its high-complexity and poor equalization performance [12], whereas UW can be regarded as a cyclic prefix of block symbol, allowing a low-complexity and good equalization performance.

Most DCS-based channel estimation methods focus on scattered frequency domain pilots [13-16]. Paper [17-18] study the design and optimization of TS applying to CS, but it is limited to independent CS and without considering the DCS situation. Reference [4]gives an example of CS-based channel estimation based on TS. It can be further modified to DCS-based, but at the cost of high-complexity equalization for diversity sequences. To the best of our knowledge, there is no references on the topic of using the TS as a cyclic prefix of block symbol and as a reference signal for DCS-based channel estimation simultaneously. Therefore, in this paper, we propose a novel method where a TS is used as both a cyclic prefix of block symbol and a reference signal for DCS-based channel estimation,whose duration time is slightly longer than the maximum delay spread. Based on SOMP [7],the performance of the measurement matrices using the proposed TS is the same as the independent measurement matrices. In short, a precise estimation of CSI can be obtained with low channel overhead.

This paper is organized as follows. Section II presents the system models of CS-based channel estimation. Section III gives the way of generating proposed TS and describes the steps of DCS-based channel estimation and FDE channel equalization based on proposed TS. Section VI provides the simulation results.Finally, conclusions are drawn in Section V.

This paper proposes a novel designed TS whose duration is slightly larger than the maximum delay spread.

Fig. 1. Frame structure of block transmission based on TS.

II. BACKGROUND

First, fig. 2(a/b) illustrates the transmission/received frame structure respectively, and the fig.2(c) give the detail about multipath interfere.

Then we give some noting about a block transmission based on TS for facilitate.

J: the TS number of a joint channel estimation frame

N: the length of data block

P: the length of TS

L: the length of channel maximum delay spread

M: the number of measurements for CS, M=P-L

K: the sparse degree of channel impulse response

i: the index of symbol block in a frame

The channel impulse response with maximum delay spread L, expressed as Hi=[hi,0,hi,1,…,hi,L]T.

The transmission/received frame S/R with J-1 block symbols plus one TS preamble, total N×(J-1)+P×J samples, expressed as

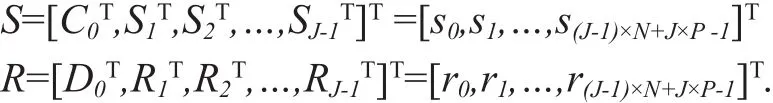
And we can get that

Fig. 2. The frame and multipath interference of the block transmission.

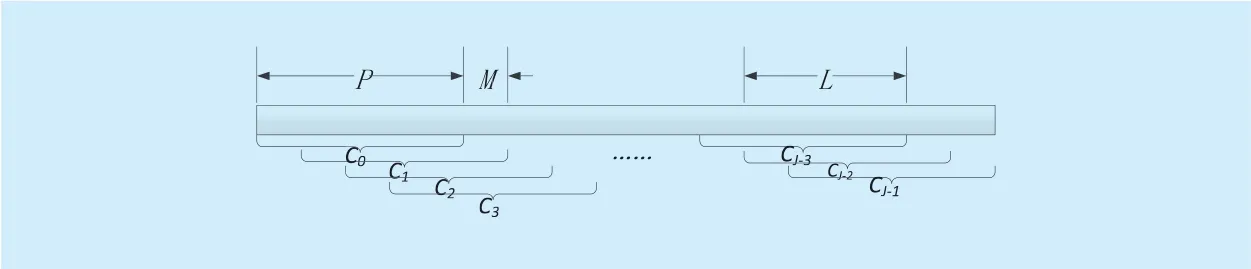
Fig. 3. The acquisition of training sequences for DCS.

The transmission/received block symbol Si/Riwith one data block and one TS, total N+P samples, expressed as

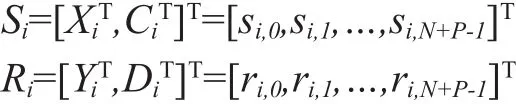
The transmission/received data block Xi/Yiwith N samples, expressed as

The transmission/received TS Ci/Diinclude first L samples CFi/DFiand last M samples CBi/DBi, total P=L+M samples, expressed as

For UW, any i and j, we have Ci=Cj, Ci-1is regard as cyclic prefix of block symbol Si.

The received block symbol Riwhich suffer multipath interfere depicted in figure2(c),includes received data block Yiand received TS Direspectively. It is clear that the last M signals of Di, DBi, are not polluted by the data block Xi, expressed as

where Nidenotes the AWGN vector, and

denotes the Toeplitz matrix determined by Ci.

If the matrix Φiis column full rank, such as DPN, Hican be estimated by conventional MMSE methods with Eq.1. On the other hand,for broadband wireless channels, only a few entries of the Hiis non-zero. It can be represented as

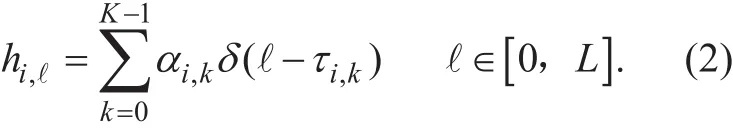
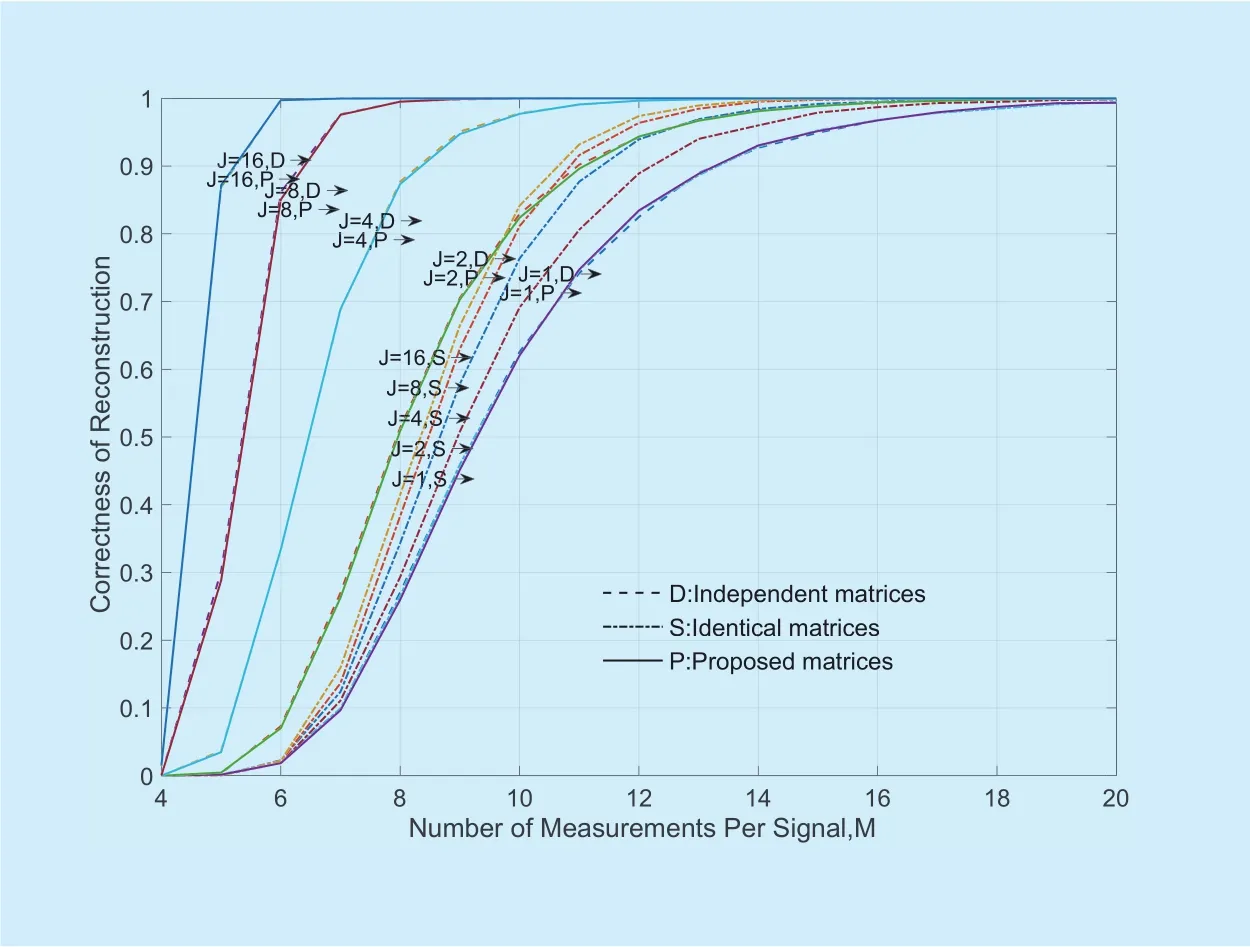
where αi,kand τi,kdenote the gain and delay of kth path, respectively. From Eq. 2, one can notice that the No. τi,kentries of Hiis αi,k, and the others are zeros, which in turn defines the number of non-zero entries as K. Defining the path gain set as Ai={αi,0,αi,1,…,αi,K-1} and the path delay set as Ωi={τi,0,τi,1,…,τi,K-1}, we call Ωias the support set of Hi. Usually, K<

Normally, the channel impulse responses are correlated among the adjacent channel measurements instances: in a frame, the multipath delay sets of H are identical (Ωi= Ω,0≤i≤J-1), which satisfies the jointly sparse model JMS-2 given in [7]. It thus indicates that they have common support set. Hence,jointly sparse estimation is feasible. Therefore,MMI-based channel estimation simplifies the problem on evaluating 2JK variables Ωiand Aiinto the problem on evaluating K variables Ω and JK variables Ai. In this processing manner,one has to evaluate the common support set Ω of K variables by combining J measurement vectors. Since the number of the key variables has been greatly reduced, the desired number of measurements in each channel measurement instance are reduced, too.

In MMI-based channel estimation, we can estimate Ω by combining J Eq.1 with measurement vectors DBiand measurement matrices Φiwhich is determined by Ci. For any given i and j in UW, Ci=Cj, means Φi=Φj, which belongs to MMV model. Its performance is weaker than DCS.

The method of channel equalization is applied after the acquisition of CSI. Based on UW, the block symbo lwhere ⊗ indicates cyclic convolution, FDE can be applied directly. Based on the conventional diversity sequence, the equalization of Riincludes:

1. Reconstruct the TS multipath interfere in Riby Hi, Hi-1, Ciand Ci-1

2. Subtracting the reconstructed TS multipath interfere from received block symbol Ri.The remaining signal of Riis the multipath propagated version of Xi.

3. The remaining signal of Rican be taken as a zero padding block symbol, which carries out FDE using FFT.

III. PROPOSED CHANNEL ESTIMATION AND EQUALIZATION SCHEME

As described in section II, MMI-based channel estimation based on UW is categorized as the MMV model. Its performance is weaker than that of DCS models. The conventional diversity sequence increases the complexity and deteriorates the performance of equalization.Here, we design a TS construction method and transmission frame. Based on the proposed TS, we can get the DCS-based channel estimation performance and the same equalization performance and complexity as UW.

In the CS measurement matrix,Toeplitz-structured matrix entries are not fully independent, because most entries share the same values among adjacent columns. However, from the same distribution, Toeplitz-structured matrices with entries drawn independently have the same measurement matrix performance as the matrices with entries fully independent and identically distributed (i.i.d)[19]. As we know, Toeplitz-structured measurement matrix can be obtained from i.i.d entries sequence by slide windows. In the light of this, the diversity measurement matrix sequence can be obtained from Toeplitz-structured matrix by slide windows.

The proposed TS can be created as follows:Firstly, the i.i.d entries sequence T with length L+JM should be generated, T=[t0,t1,…,tL+JM-1]T.Then, as illustrated in figure 3, each TS Ci=[ci,0,ci,1,…,ci,P-1]Tcan be acquired through slide window reading from T, the window size is P=M+L and the slide gap is M each time,ci,p=ti×M+p. Obviously, the first L samples of the current TS are the same as the last L samples of the previous TS, which is [ci,0, ci,1,…, ci,L-1]=[ci-1,M,ci-1,M+1,…,ci-1,P-1].

Fig. 4. The proposed symbol detail.

Algorithm 1. Generation algorithm of proposed TS and measurement matrix.Inputs:The system parameters J/L/M Output:1) The transmission TS Ci, 0≤ i ≤ J-1 2) The measurement matrix Φi, 0≤ i ≤ J-1 1: Generate i.i.d entries sequence T([0:L+JM-1])2: Generate Φ([0:M-1], [0:L+(J-1)M]) from T by Eq 4 3: for i =0:J-1 4: Ci = T(iM+[0:L+M-1])5: Φi = Φ([0:M-1], (J-i-1)M+[0:L])6: end Algorithm 2. Channel estimation and equalization algorithm based on proposed TS.Inputs:1) The system parameters J/N/L/M and set P=L+M 2) The received frame R(0:(J-1)×N+J×P-1)3) The measurement matrix Φi, 0≤ i ≤ J-1 Output:The equalized data block Xˆi, 1≤ i ≤ J-1 1: for i= 1:J-1 2: Ri= R(P+(i-1)(N+P)+[0:N+P-1])3: Ri’= Ri(0:N+L-1)4: DBi= Ri(N+L+[0:M-1]:)5: end 6: Estimate Ω from DBi and Φi by SOMP 7: Calculate all Ai from Ω and Φi by MMSE 8: Reconstruct all Hi from Ω and Ai according to Eq.2 9: Equalize all blocks Ri’ from Hi by FDE according to Eq.3, and get the load data estimation value Xˆi

After obtaining all TSs Ci, the proposed transmission frame is constituted of J TS Ciand J-1 data block Xiaccording to figure 2(a).A block symbol detail shows in figure 4(a).Fig. 4(b) exhibits the received block symbol that suffers from IBI which is introduced by multipath propagation. The short version transmission/received block symbol Si’/Ri’ expressed as

There are the same sequence CFithat is in the front and back of data block Xi. In other words, CFican be taken as cyclic prefix of Si’in FDE. So

Base on proposed TS, measurement matrix Φiof MMI-based channel estimation can be constructed in this way: First, give the Toeplitz-structured matrices corresponding to sequence T:

Then, reading from Φ through slide window with the size of M×(L+1), from right to left, by M gaps each time, one can get matrix sequence Φi. The generation of proposed TS and measurement matrix is illustrated in Algorithm 1.

Although many columns of adjoining Φiare identical, for the same index, the columns of different Φiare independent parameters. The matrix sequence Φiresembles a 3D-Toeplitz-structured matrix. Simulations at section IV show that they achieve identical performance of i.i.d Gaussian matrixes in terms of Ω correctness of reconstruction with SOMP.

In receiver, based on the proposed TS, the processing steps of the DCS-based channel estimation and FDE equalization are illustrated in Algorithm 2.

From the above we can see, for MMI-based channel estimation and FDE equalization, the differences between the proposed TS and the UW are the novel methods of TS design and the measurement matrix sequence construct,which should treat off-line. However, the channel estimation and equalization processes are identical. Hence, the on-line complexities are similar.

IV. SIMULATION AND DISCUSSION

In this section, the performance of SOMP based on the proposed TS is investigated,including the correctness of Ω estimation(namely correctness of reconstruction), estimation MSE of H and BER with Uncoded QPSK. The Wide Sense Stationary Uncorrelated Scattering (WSSUS) channel model is adopted in this simulation. The maximum delay spread length is 5ms, a normal value for ionospheric channel, the channel sparsity K=4 or 6, the Doppler spread is 1Hz and the gain is independent for different propagation paths. The signal bandwidth is configured as 19.2 kHz, Uncoded QPSK scheme is adopted.Supposing that the synchronization is perfect,i.e. τ0=0, the remaining path delays, τ1, τ2, ...,τK-1,are randomly selected from 1 to 95 and all path gains αi,0, αi,1, ..., αi,K-1are independent random complex numbers. In SOMP based on the proposed TS scheme, the J measurement matrices Φiand TSs Ciare constructed according to Algorithm 1. In SOMP based on the UW scheme, a Toeplitz-structured matrix Φiwith Gaussian distributed entries, as the measurement matrix, is generated and invariant at each i from 0 to J-1. Some performance of the SOMP with independent Gaussian matrices,independent CS and conventional MMSE are calculated for comparison.

Fig. 5 and figure 6 show the correctness of reconstruction performance comparison among independent matrices, identical matrices and proposed matrices with K=4 and K=6. It is clear that the correctness of reconstruction based on proposed matrices agrees with the independent Gaussian matrices, while the performance of identical matrices can’t get significant benefits with J increasing. For 99.9% correctness of reconstruction, the desired number of measurement among different reference signal (corresponding to different matrix) and channel estimation algorithm can be summarized as below:

Fig. 5. Correctness of reconstruction comparison with K=4 and noiseless.

Fig. 6. Correctness of reconstruction comparison with K=6 and noiseless.

1. For UW reference signal, independent OMP(J=1) channel estimation algorithm, the de-sired number of measurements M is 26 with K=4 and M is 34 with K=6.

Fig. 7. MSE performance with SNR=15dB.

Fig. 8. BER performance with SNR=20dB (Uncoded QPSK).

Fig. 9. MSE performance with M=3K.

2. For UW reference signal, SOMP (J=16)channel estimation algorithm, the desired number of measurements M is 15 with K=4 and M is 19 with K=6.

3. For proposed reference signal, SOMP(J=16) channel estimation algorithm, the desired number of measurements M is 7 with K=4 and M is 9 with K=6.

Figure 7 shows the MSE performance comparison among independent OMP, SOMP based on UW, and SOMP based on proposed TS with a varying number of measurements when SNR is 15dB invariably. Fig.8 shows the BER performance comparison among them with uncoded QPSK when SRN is 20dB. It is clear that the proposed scheme performs better than others when the number of measurements is small, e.g., M<4K. The MSE performance still approaches the theoretical Cramer-Rao lower bound (CRLB) when the number of measurements becomes less. The BER performance always approaches the ideal CSI case too. This mean that for a given MSE requirement, the proposed scheme need fewer TS overhead due to artifice of the proposed frame structure.

Figure 9 compares the MSE performance among independent OMP, SOMP based on UW, SOMP based on proposed TS and conventional MMSE based on DPN with a varying SNR when the number of measurements is 3K invariably. Fig.10 shows the BER performance comparison among them with uncoded QPSK. It can be observed that the performance of proposed scheme is observably better than other CS scheme. The MSE performance still approaches the theoretical CRLB when SNR high. And the BER performance also approaches the ideal CSI case always. This is because the path delays of channel can be reliably estimated even the number of measurements is only 3K. Moreover, MSE performance of the proposed scheme outperforms the conventional MMSE based on DPN by more than 3dB and BER performance outperforms by about 1dB at the target BER of 10-2while the length of proposed TS is much less than DPN.

Fig. 10. BER performance with M=3K (Uncoded QPSK).

V. CONCLUSION

This paper proposes a novel designed TS whose duration is slightly larger than the maximum delay spread. As a reference signal,DCS-based channel estimation can be used to reduce the channel overhead. As a guard interval, the FDE can be applied directly to the block symbol, and a cyclic prefix structure is formed. The simulation results proved that, based on the proposed TS, the measurement matrix shares the same performance as the independent measurement matrix, and the SOMP algorithm can reduce the number of measurement M substantially meanwhile maintain perfect channel estimation performance. The block transmission based on the proposed TS can reduce the reference signal overhead, leading to the improvement of the channel utilization.

ACKNOWLEDGEMENTS

This work is support by National Key Technology Research and Development Program of the Ministry of Science and Technology of China (2015BAK05B01).