A Fairness Resource Allocation Algorithm for Coverage and Capacity Optimization in Wireless Self-Organized Network

Pan Zhao, Lei Feng, Peng Yu, Wenjing Li,＊, Xuesong Qiu State Key Laboratory of Networking and Switching Technology, Beijing University of Posts and Telecommunications,Beijing 00876, China

2 Henan University of Technology, Zhengzhou 450007, China

Abstract: To achieve the higher resource efficiency, Coverage and Capacity Optimization(CCO) as an important role of the network self-healing and self-optimization, has become a focus topic in wireless Self-Organized Network (SON). In this paper, a novel CCO scheme is proposed to maximize utility function of the integrated coverage and capacity.It starts with the analysis on the throughput proportional fairness (PF) algorithm and then proposes the novel Coverage and Capacity Proportional Fairness (CCPF) allocation algorithm along with a proof of the algorithms convergence. This proposed algorithm is applied in a coverage capacity optimization scheme which can guarantee the reasonable network capacity by the coverage range accommodation. Next, we simulate the proposed CCO scheme based on telecom operators’ real network data and compare with three typical resource allocation algorithms: round robin(RR), proportional fairness (PF) and max C/I.In comparison of the PF algorithm, the numerical results show that our algorithm increases the average throughput by 1.54 and 1.96 times with constructed theoretical data and derived real network data respectively.

Keywords: self-organized network; coverage and capacity optimization; resource allocation algorithm; user fairness.

I. INTRODUCTION

With the rapid growth of users and services in cellular networks, mobile operators and manufacturers have to develop mobile communication systems with greater capacity and improved coverage. In parallel, the complexity of these systems makes the network management a challenging task [1]. For this reason,operators search intelligent and autonomous technology for configuring network parameters to enhance network performance without increasing costs and human intervention.

To address this problem, the concept of Self-Organizing Network (SON) is developed as one important part of the 3GPP Release 8 to enhance the operability of mobile radio access networks [2]. The SON is utilized to boost the network operator targets, referred to as Key Performance Indicator (KPI). Self-Organizing Network (SON) consists of self-configuration,self-optimization, and self-healing. Self-optimization is investigated in LTE, femtocell,device-to device (D2D), and fifth generation(5G) networks [3] [4]. Coverage and capacity are two key network performance indexes which are not only affected by the network planning work but also the dynamic radio environment. Since addressing the changed situation manually is very expensive and time consuming. Coverage and Capacity Optimization (CCO) as an important self-healing and optimized use case of the Self-Organizing Network (SON), is considered to be a key enabler for 4G LTE advanced and 5G cellular systems.

The Third Generation Partnership Project(3GPP) TS32.521 [5] introduced the CCO use case for Long Term Evolution (LTE) under the topic of SON. Mobile operator have identified CCO as one of the most important use cases of self-organizing network (SON). The aim of CCO is to provide optimal coverage and capacity, so that network throughput and capacity are maximized while ensuring a certain service confidence level. [6].

1.1 Related Work

Several works have recently investigated and contributed to self-configuration and self-optimization in wireless communication networks to resolve user association, resource allocation, power control, interference mitigation,spectrum reuse, network selection and/or admission control.

Combining Markov approximation and non-cooperative game theory, the author in[7] studied a self-organization algorithms for traffic offloading in Heterogeneous Networks,jointly considering interference mitigation,user association and resource allocation under QoS guarantee. A cognitive and cooperative SON framework is proposed to predict system behavior in [8] for 5G mobile radio access network. The authors in [9] developed an autonomous resource allocation scheme to suppress interference of vulnerable Pico Base Stations and reached self-organizing solutions for Heterogeneous Networks. In [10], the authors considered a fairness distributed algorithm for power adjustment in two-tier femtocell networks under imperfect channel state information. A self-organizing schemes were proposed to combat energy consumption utilizing non-cooperative game and no-regret learning algorithm is given in [11]. The authors in [12]focused on secure resource allocation in twoway relay wireless sensor networks. In [13],the authors used the cooperative Nash bargaining game theory approach to reach a self-organizing solution for sub-channel and power allocation. However, our work is mainly focus on self-optimization with respect to automatic CCO.

In this paper, the authors propose a fairness allocation algorithm CCPF for CCO solution.

Besides above works, there are still many literature studies on CCO research, the authors in [14], [15] provided an effective tilt-based SON algorithm to implement CCO. The authors in [16] used 2-dimensional antenna arrays for concurrent coverage since it achieves better performance than linear arrays. These work considered that the cells overlapped area could be effectively reduced, because LTE adopts the hard handover manner instead of soft one. But they ignored that the network essentially followed a trend of smaller and denser cells planning as its coverage criterion,so these LTE adopts the hard handover manner instead of soft one. But they ignored that the network essentially followed a trend of smaller and denser cells planning as its coverage criterion, so these methods easily leaded to the coverage hole problem. Moreover, the margin of antenna tilt control was finite in the real network. On the one hand, studies in[17], [18] mainly optimized the CCO triggering process in the view of system learning.This type of method needed the cooperation with the network management system and antenna system. On the other hand, problem was that these work ignored the sacrifice of the edge users’ throughput. The authors [19]gave a comprehensive configuration optimization including both antenna tilt manner and transmitting power manner. Although it gave an excellent performance validation of the optimization method, it also ignores the edge users’ throughput performance. The authors in[20] used α-PF allocation algorithm to achieve CCO. However, it directly employed the ca-pacity gain to measure the coverage effect,which was not very accurate and reasonable.

1.2 Contributions

According to the above work, we can conclude the major problem of the previous researches.They mainly focused on the method to operate CCO but ignores the sacrifice of the edge users’ throughput after CCO. This causes the decrease of the cell mean throughput due to a high proportion of edge users after CCO. To solve this problem, our work has the following contributions:

1) Suggest a novel resource allocation algorithm that allows a balance between coverage and capacity. This algorithm improves the traditional proportional fairness algorithms [21]by taking account of the user’s received signal power when assessing the user’s scheduling priority. The reason is that the user’s received signal power, as an important coverage indicator, can directly reflect the actual users’position within the cell’s service area. Then it uses a β-parameter linear weighted approach to consider the service received signal power(coverage) and throughput (capacity) together when resource allocating. This novel resource allocation algorithm is called as Coverage and Capacity Proportional Fairness(CCPF).

2) Introduce a traffic triggered and transmitting power controlled scheme to achieve CCO and apply a proposed allocation algorithm named CCPF to schedule the resources after CCO. This scheme can increase the likelihood of being allocated for the edge users. As a result, the mean throughput of both edge users and cell users can get increment, whose target is solving the traditional CCO’s problem.

The rest of the paper is organized by follows: In Section II, a novel design for resource allocation algorithm is proposed. The convergence of this algorithm is proven in Section III. On the basis of the improved algorithm,the corresponding coverage and capacity optimization mechanism in SON is given in IV.Section V discusses the simulation results.Finally, Section VI concludes the paper.

II. CCPF RESOURCE ALLOCATION ALGORITHM

Assume that there is a cell having M users and the buffer of the cell is infinite. It means the call admission control problem does not need to consider [22]. For the cell downlink resource allocation process, the scheduler chooses a user to assign the resources within some TTIs (ms). The resources allocation symbol {Wtn+1=m,n ∈ N,m ∈M} represents the scheduler chooses the user m to assign resource at the time tn+1. Let pm,tn+1and rm,tn+1denote the instantaneous service received power(dBm) and instantaneous throughput (Kbps)at the time tn+1respectively (notice that the received power is the sum power of all PRBs allocated to user m); πm,tnand θm,tnare the mean service received power (dBm) and mean throughput (Kbps) in the time-interval [t0,tn]which is executed by the sliding window. The reference initial time is t0. According to the physical meaning of the network, we know that θm,tn＞0 and πm,tn＜0. Assume that the scheduler has the complete channel knowledge, namely any users measurement report can reach the Base Station (BS) with no error.Hence the throughput and service received signal as the reference information effectively is applied in the allocating process. Referring to [23], we can have the following recursive formula of mean throughput for user m:

2.1 Problem formulation

where εnis the sliding window decided by the QoS requirement, whose value is always small, so here we take it as εn=(n+1)-1. δ is the Kronecker sign function to represent whether the scheduler chooses user m at the time tn+1. From [23], we can know (1) is the criteria of the throughput proportional fairness(PF). Since the PF algorithm and other similar algorithm based on it like α-Fairness [24] only consider the effect of the throughput, they ignore the user’s actual location in the cell.However, the throughput and service received power are not completely linear [25]. Therefore, these algorithms cannot enhance the cell edge user’s throughput effectively. To solve this problem, this paper introduces the factor of the service received signal power to improve the allocating algorithm while reserving the fairness caused by the throughput. This is due to the user’s service received signal power will increase if they get more time-frequency resources in wireless network. Thus, the introduction of this factor can enhance the scheduling priority of the edge users on the basis of PF. Firstly we let the scheduler monitor the mean service received power every allocating time. Then we can have the recursive formula of mean service received signal power for user m:

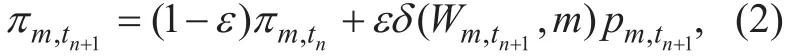
where ε is decided by the time-dependency of the service signal. For the convenience of analysis, we think the variation of the service received signal power is only determined by the amount of the assigned resources. Here we take ε=εn= (n +1)-1. This paper expects to consider both the coverage (received signal)and capacity (throughput) in the resource allocating process. So we define the metric zm,tn+1,ζm,tntaking account of both the coverage and capacity. As follows, zm,tn+1denotes the integrated metric of capacity and coverage for user m at the time tn+1, ζm,tndenotes the mean integrated metric of capacity and coverage for user m in the time-interval [t0,tn].

where 0 ≤ β ≤ 1 is utilized to regulate the objective ration between coverage and capacity.K1 is the unified dimension obtained by the expectation and variance or the empirical observation of the system. The Eq.(3) has another practical network meaning, when β nears to 1, the metric trends to the edge users who have a direct lower received power, and when β nears to 0, the metric trends to the central users who have a higher throughput as shown in figure1.

Combing with (3), the variation of the coverage and capacity metric Δζmfor the user m from the time tn to tn+1 can be obtained as:

where ϕm(ζm,tn)equals one if user m is scheduled and zero if otherwise.

2.2 Problem and solution

Define a utility function, satisfying the requirement of the integrated coverage and capacity through the packet scheduling, then for ζm,tnset the utility function as follow:

Our aim is to obtain the optimal solution to achieve the maximum U(ζ). Considering the metric ζm,tnas the discrimination, CCPF resource allocation algorithm is used to choose the user by a heuristic scheme to maximize U(ζ).

Assume the scheduler has completed the resources allocation by the time interval [t0,tn].It will choose the user to schedule at the time tn+1. If the chosen user is m*, then from (1)and (2) we can have the change of this user’s utility function ΔUm*(ζ) as (7) shown in the next page.

For the other users not allocated the resources, the variation of the utility function is:

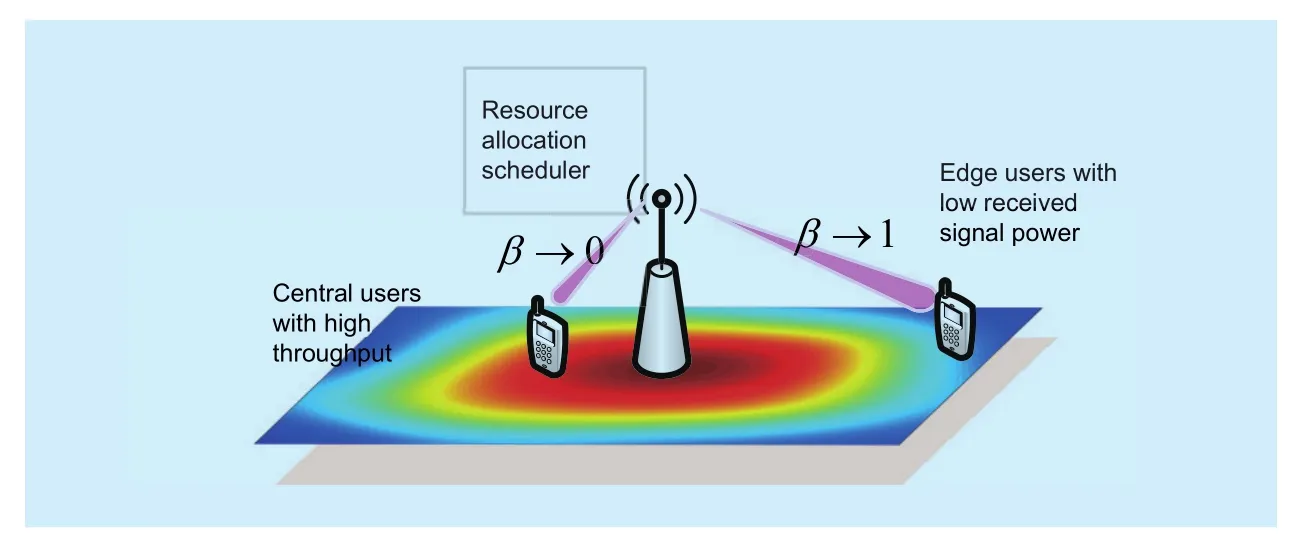
Fig. 1. Illustration of Meaning of Coverage and Capacity Metrics.

Add (7) and (8), the utility function variation of the whole cell ΔU(ζ) is shown in (9).

Table I. Parameters of system.

Equation (10) above is the criterion expression of CCPF resource allocation algorithm with taking account of both the coverage and capacity. In the following session, we discuss the convergence of this algorithm in detail.Moreover, the CCPF algorithm is used to choose user who has highest priority for larger comprehensive metric in each allocation interval. Therefore, the complexity of this algorithm is O(M), where M is represented as the total number of the users in the system.

III. ANALYSIS ON CONVERGENCE AND OPTIMALITY OF CCPF

In this section, we will present some convergence theorem for the iterative algorithm,which denote that CCPF has a unique stable point and optimizes the utility U(ζ). These conclusions rely heavily on the structure of CCPF and its relation to what are known as monotone dynamical systems.

3.1 Some definitions and theorems

The existence of a unique equilibrium is of significance for the performance analysis of the CCPF algorithm. Since ζm,tnis made up of iterative functions, the paths of ζm,tnare very close to a point ζ*, according to the characterization of the limits of the processes ζm,tnas n→∞. Based on some results from dynamical systems theory, we find that the limit point of CCFP is unique and we will prove in follow-ing.

Moreover, under broad conditions, if the tracking parameter ε and εnare small and constant, or if n is large, then the path converges to the solution to a deterministic ordinary differential equation, which is computed from the mean dynamics of the process. As we have just remarked, the path will essentially follow the solution to the ordinary differential equation (ODE)ζ˙ =g(ζ). For any initial condition,converges to the set of limit points of the solution of the solution of the ODE ζ˙ =h(ζ) -ζ according to a standard result in [23]. Then the ODE has a unique equilibrium point and it will be proved.

According to [23] and [25], we have the following definitions and theorems:

Theorem 1. For ODE ζ˙ =g(ζ), if satisfies Condition (i): g(ζ) is continuous; Condition(ii): the solution of ζ˙ =g(ζ) is unique for each initial point; Condition (iii): ifandthenwhich is also named as Kamke condition;Condition (iv): For 0≤t≤T and ξ∈(ℝ+)n, the ODE solutionis continuous dependent on the perturbation ζtn′+ξ of the initial point. Thenis monotonous.

Theorem 2. If ODE ζ˙ =g(ζ) satisfies Kamke condition, then any solutions for the initial points ζtn′that satisfy g(ζ)＞ 0 are convergent to an equilibrium point.

3.2 Convergence and optimality of CCPF

To prove the convergence of CCPF, it is necessary to prove the monotonicity of the solution to the ordinary differential equationg(ζ). According to Theorem 1, if g(ζ) is continuous, the solution of the ordinary differential equation is unique, g(ζ) satisfies Kamke condition, and the continuity of the solution of the ordinary differential equation depends on initial value, then the solution of the ordinary differential equation is monotonous.

Table II. Parameters of proof.

According to the proof of Appendix A and Theorem 1, it is well known thatis monotonous fond if tn=0, for any users it hasFrom Theorem 2 we learnis convergent to an equilibrium point ζ* at each tn.Now proveis also convergent tofor any initial conditionTake an elementfrom the quasi-convergence set Q. According to Theorem 3, set Q is dense. Then it has 0＜From Theorem 4, we know. Assume in E setwhich satisfies the Conclusion 4-1 in Theorem 4. However,from the convergence of hand the characteristic of the equilibrium point, it exists bothandTherefore, Conclusion 4-1 is not true. Then from Conclusion 4-2 in Theorem 4, we have L(0) =. So for any initial conditionit existsFinally,we showcan achieve the maximum of the utility function. Assume every user has reached toat the initial time tn=0. Differentiate the utility function in (7):

Suppose the system can achieve the maximal metric ζMax. From the denseness of set Q it has ζMax≥ ζ*. The scheduling Kroneck sign function forSo we have

From the above formula, we learn that ζ*can make the U(ζ) to reach the maximal utility. Hence CCPF algorithm introduced by this paper is convergent.

IV. COVERAGE AND CAPACITY OPTIMIZATION SCHEME

4.1 Performance metrics

Firstly, we show the closed-form expressions for the performance metrics before giving the CCO scheme. The performance metrics are consist of two perspectives: Coverage metrics and Capacity metrics.

Coverage metrics: The received signal power is utilized to evaluate the performance of coverage. Assume each downlink time-slot has a total bandwidth W. For a cell owning M users, we assume that the transmitting power of Reference signal (RS) is same with the normal service signal in a Physical Resource Block (PRB). Let the total transmitting power of a PRB is Psand the transmitting antenna gain is Ga. Then the received signal power for user m is:

where NPRBis the number of PRB allocated to user m; Lmis the path loss of user m, it is rely on the distance between the user m and the base-station, the downlink working frequency, the height of the base-station, the shadow fading loss; ρmis the impact factor of the fast fading. Since the channel has the Rayleigh nature, U=ρm2owns the exponential probability density function:

Capacity metrics: To evaluate the performance of capacity, the user’s throughput and cell’s Resource Occupation (RO) ratio is used.Firstly, we can obtain the signal to interference plus noise power ratio per unit PRB as follow:

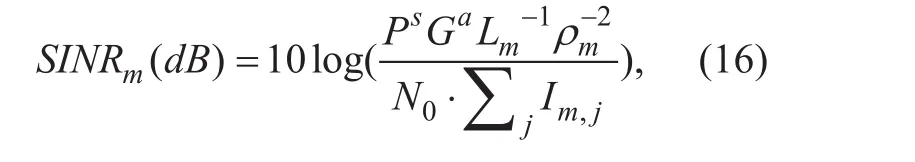
where N0is the Gaussian white noise; Im,jis the interference to user m from the neighbor BS j. The element of the adjacent base-station set is decided by whether its interference intensity is submerged by the white noise N0.We can obtain Im,jby:

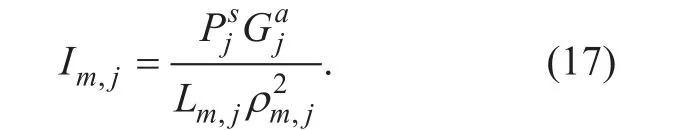
For simplicity, we consider the fast fading effecbrought by the neighbor BSs can be eliminated by the inter-cells interference suppression technology [20]. Then the throughput for a user m can be written by Shannon theorem as:

The CCO has strength to make the traffic in each BS more reasonable. Hence we not only concern the capacity performance for users but also consider the BS’s traffic situation after CCO. So we can find the total traffic for BS j is:

where λmis the service arrival rate of user m and µjis served rate of BS j for each user. If we have a traffic limitloaded by BS j,then we can get the RO ratio for BS j is:

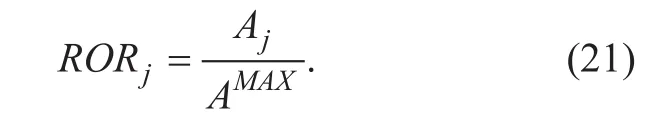
4.2 Problem description

Our aim is to make the network system get an excellent trade-off between coverage and capacity according to the varied traffic load.Firstly, we need a CCO control scheme which can make BS’s RO reasonable. After CCO,the allocating algorithm CCPF is used. Then the evaluation of the user’s performance by the trade-off between coverage and capacity is needed. Although we have given the coverage and capacity metric ζm,tnin CCPF, it does not have any practical network meaning.The reachable throughput of the users in [20]is used to show whether the user is covered by the BS. However, this is not coincident with the real wireless system and it cannot be adjusted. Therefore, our paper uses the edge users’ received signal power to determine whether the user is covered which is same with the real network. Define pmin, if the user’s received powerthen consider this user is covered; Define rminis the user’s minimal demanded service throughput. Ifthen consider this user accessing to the system cannot obtain an excellent throughput experience.

4.3 CCO control scheme

We give a CCO control scheme consisting of traffic triggered process, transmitting power adjusted method and the novel proposed CCPF algorithm. The main steps are:

Step1: Firstly, the system monitors the service traffic differences between source BS and another neighbor BSs. This can be achieved by the inter-cell interface like X2 in LTE network. When the traffic of the source BS is lower or higher than the traffic of the neighbor BSs by a specific threshold THtrafficat a continuous time interval ΔT, the power accommodation will be triggered. The time-scale of ΔT is always too larger than the TTI scheduling level. Otherwise, the CCO control scheme will be triggered frequently, that easily causes the conflict with the following steps;

Step2: Increase or decrease the transmitting power of the source BS by a specific power step Pstep, and calculate the new set of the users covered by it;

Step3: According to the new set of the users in the source BS, regulate the β parameter in CCPF by step βstepto make the users satisfy the requirement on the throughput. And then repeat Step 2 to continue covering the users in neighbor BSs or to handover the users in the source BS to another neighbor BSs until all the users in each cell can satisfy the requirement on the throughput.

The detailed COO scheme and the CCPF algorithm are shown in Algorithm 1 and Algorithm 2, respectively. (Recover process is similar)

V. NUMERICAL RESULTS

In this section, we evaluate the performances of CCPF resource allocation associated with CCO in LTE network simulation environment.We conduct the evaluation from two aspects.In specific, 1) One scene is a regular 6+1 BSs sim-scene which only contains one central BS and 6 neighbor BSs. 2) Another scene is from a real-world network area, i.e. Beijing e-Town.The data of BSs and traffic are all provided by some China telecom operators. This further demonstrate our method in practicable scene.

5.1 “6+1” Base-station sim-scene

Algorithm 1. Scheme of coverage and capacity optimization.1 Initial Phase:2 Step 1: Monitor the service traffic difference between the source BS and another neighbor BSs.3 for T t T T＜ ＜ +Δ 4 if ∑ j∈Jη η initial n initial-· ≥ by (27)5 Then Go to Step 2 6 Step 2: Accommodate the transmission power of the BS in order to cover the users in the neighbor BSs.7 P P P j n j n traffic() ()t N t TH= + // Accommodates power by specific step 8 for any user m do 9 If Ep p s s step n+1≥ by (26) then //Verify whether users is covered or not by new transmission power 10 Then add m to Μ 11 end if 12 end for 13 Μ = Μ+m; // New user coverage set 14 Step 3: Adjust β to enhance the scheduling priority of cell edge users and allocate resources using CCPF algorithm 15 Repeat Phase: Repeat Step 2 until Step 3 cannot be satisfied even by, then Repeat Step 1( )m,t min Algorithm 2. CCPF algorithm.1 Initial Phase:2 β=β+βstep// Adjust β factor by specific step 3 For t ＜ TTI //Whether reaches the TTI threshold 4 n ps by (10) // CCPF algorithm 5 if m=m*6 Calculate zm,tn+1 by rm,tn+1 and pm,tn+1 ζ εζ ε m∗=argmax n+1 0≤m≤M zζm,t m,t n(1 ) z by (5)7 else ζ εζ mt n mt nmt,n+1= - +,n ,n+1 n+1=(1- ) by (5)8 n=n+1 //Update the system time 9 end For;10 Repeat phase: Repeat until all users m∈M, Er r mt n mt,,n n+1≥ by (19) //Users in the coverage set can satisfy the requirement on throughput( )m,t min

Simulation Settings: The regular “6+1” BSs scene is shown in figure2.a) that contains one central source BS and six neighbors BSs around. Each BS takes the single antenna transmission mode and owns the same amount of physical resources. Assuming the initial user positions are random and these positions do not vary before and after optimization to avoid the affection which is generated by the Winner-II channel characteristic [26]. The typical Cost-231-Hata propagation model and real 2.6 GHz LTE are considered. The traffic intensity curve is generated by the method in[27] as shown in figure2.b). The red-dotted line represents the traffic arrival intensity varying with the time of the central BS while the green-solid line represents it of the neighbor BSs.

Result Analysis: In the simulation scene,the central source BS firstly operate the CCO process in Scheme1. From figure2.b) we can see during a time interval ΔT, the traffic difference Δη between the source BS and the neighbor BSs is larger than a threshold THtraffic.Then it executes CCO process i.e. Step 1 in Scheme 1 when condition satisfied. Corresponding, the central source BS improves its transmission power through Step2 as shown in figure3. As a results, the user received the signal power of the adjusted central source BS gets an improvement. The power in the central source BS cell’s edge reaches -87dBm which is good enough to provide the wireless service. The improvement of the transmission power make the central BS absorb more users from the other neighbor BSs. Fig. 3 also gives the user association comparison before and after COO. From the results, we see that the central BS increases more than 30% of the edge users than the case before CCO. Since the purpose of CCO is to obtain more reasonable resources utilization, Fig. 4 gives the RO ratio comparison before and after CCO. It can be seen that according to our traffic arrival intensity settings in figure2.b), the neighbor BSs have a “heavy” RO that is higher than 80%and the central source BS has a “light” RO before CCO process. But after CCO, we see that all the BSs’ RO have a more reasonable and equalizing performance, which means we get a good balance between coverage and capacity as a whole.

However, there is still a problem. The proportion of the cell edge users to all the served users will increase significantly, when CCO process is carried out in a region, as shown in figure4. If we still use the traditional resources allocation algorithm, the edge user will own a low scheduling priority. As a result, we cannot obtain an excellent performance of the user throughput. To cope with it, we adopt CCPF after CCO, i.e. Step3 in Scheme 1 increase the edge users’ scheduling priority. By adjusting parameter, it makes the resource assignment reasonable when considering both coverage and capacity factors.

Fig.5 analyzes the performance of throughput between CCPF and typical resource allocation algorithm [28] i.e. RR, PF and Max C/I.This figure shows that the throughput of the edge users on CCPF reaches 7.2Mbps which is increased by 2.11 and 2.57 times compared with PF and RR respectively. Max C/I has a zero edge user throughput performance because it just takes care those central users with highest C/I. Moreover, the mean throughput of CCPF can reach to 10.1Mbps. It increases by 1.34 and 1.61 times than PF and RR respectively. The reason is the proportion of the cell edge users to all the served users increases a lot after CCO. So the increment of the edge user throughput will also make the mean user throughput rise. For comparison of the peak throughput, Max C/I is considerably better than PF, RR, and CCPF. Due to assign more resources to the edge users, CCPF algorithm has the lowest peak throughput performance that is equal to 95.2% and 90.3% of performance on PF and RR respectively. But the user in the peak point always has a high C/I,so the loss of the peak throughput performance is not obvious.

Fig. 2. Simulation scene settings.

Fig. 3. User Association Comparison before and after CCO.

Fig. 4. Resource occupation comparison before and after CCO.

Fig. 5. Throughput comparison among CCPF, RR, PF and Max C/I.

Fig. 6. Beijing e-town BSs traffic distribution before.

5.2 Real network data sim-scene

Simulation Settings: We choose Beijing e-Town area as the simulation scenario to be investigated. It consists of 24 macro-BSs (This paper does not consider the affection of the micro-BS). The data is collected from some China telecom operators. Due to emerging business area, some BSs in ETown carry a high traffic load in the weekdays. We select the BS traffic load data at a busy hour 10:00 am on a certain Wednesday and use the Erlang C equivalent traffic model to calculate the number of the users served by BSs. The traffic distribution is showed in figure6 at this given time. It is obvious that some BSs have a high traffic (more than 0.45Erl/m2). The real OMC system interface can only provide the data hourly. But the CCO process is working on a TTI ms time-scale. So we take this 10:00 am data as the CCO process triggering input and adopt a TTI-level LTE system simulator [29]to deal with the whole real simulation scene.We set 2*2 preceding antenna transfer mode,20MHz total system bandwidth; 2600MHz working frequency and 5km/h Winner II channel model.

CCO Result Analysis: In figure7 the performance of the coverage and traffic loaded of BS after CCO process is observed. Compared with the pre-optimization case in figure 6, we can see the low traffic loaded BSs balance the high traffic loaded BSs’ load through the transmission power accommodation, then the RO of the whole area is more reasonable. We also concentrate on the edge user and mean throughput performance by CCPF allocating.Fig. 8 shows the throughput CDF curves of different packet scheduling algorithms. As same as other research works, we use 5%point of CDF to define the edge user throughput performance. Obviously, the performance of CCPF is better than PF, RR and Max C/I.Except for Max C/I (only ensure the central user to get a high mean throughput), CCPF can improve the mean throughput performance by 1.54 and 1.96 times compared with PF and RR respectively. The result is better than the 6+1 BSs scene because 1) both the scale of network and the number of served users are larger; 2) the 2*2 MIMO mode is applied in this scene. To measure the allocating fairness among the users, Table III gives the Jain’s Fairness Index comparison among each allocating algorithm [30]. The ideal case of fairness is achieved when this index is equal to 1 while decreasing fairness is refl ected with decreasing value of the index. It can be seen that the proposed algorithm forms the better users allocating fairness than Max C/I and PF algorithm while the RR algorithm gets the highest score of fairness. It is consistent with the above throughput performance analysis.

VI. CONCLUSION

In this paper, we propose a fairness allocation algorithm CCPF for CCO solution. Our main contribution is to consider both received power and throughput when resources allocated and use the β linear weighted method to structure the scheduling criterion. The theoretical analysis shows the utility of integrated coverage and capacity can reach optimal solution with our criterion. Then we give a CCO control scheme associated with CCPF and verify the performance by simulating the scheme in a constructed “6+1” BSs scene and a Beijing e-Town real network scene. The simulation results show our method can get more reasonable BS’s RO ratio and better user’s throughput performance. The further research work will focus on how to apply the proposed allocating algorithm and CCO scheme to the Het-net that means to consider the effect of microcell and pico-cell. In addition, we will also research on the association optimization with different CAC mechanism.

ACKNOWLEDGMENT

This paper is supported by the 863 Program(2015AA01A705) and NSFC (61271187).

Fig. 7. Beijing e-town BSs traffic distribution after CCO.

Fig. 8. Throughput comparison in Beijing e-town scene.

Table III. Fairness for different algorithms.

Appendix A

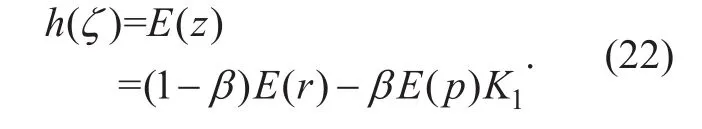
Here, z, r, p are parameters, they are related toSince ζ˙=g(ζ),then weTo analyze the convergence, we firstly need to prove the continuity of g(ζ) i.e. h(ζ). As stated in Appendix B, it is easy to learn h(ζ) is Lipschitz continuous, then g(ζ) is Lipschitz continuous, too.

1. Continuity

Let h(ζ) denote the expectation conditioned of z, suppose that the channel satisfies the Rayleigh or Rice characteristic, and then we have the expectation of z:

2. Uniqueness

After proving the continuity, we will perform the optimal proof of CCPF. At any time tn′, we build the Cauchy problem of g(ζ) as the followed equations set:

According to Picard existence and uniqueness theorem, it has the unique solutionfor the initial condition ζtn′in the time-interval tnespecially T→∞for tn′=0. Then for tn∈[0,+∞) it owns the unique solution ζ( tn|ζ0= 0). In the following discussion, we will analyze the monotonous of

3. Kamke condition

For the Theorem 1, Condition (i) (continuity)and Condition (ii) (solution uniqueness) have been proven. And for Condition (iii) (Kamke condition), it existsfor any two time tn′ and tn′ + T. If for the same user m we havethen from (10) we can know the probability of the user being scheduled is higher at the time tn′ + T than tn′ which means:

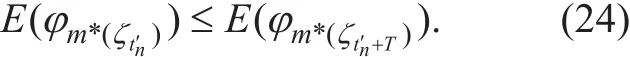
4. Perturbation on the initial point

Finally verify the Condition (iv) (perturbation on the initial point). For two initial conditions ζtn′1and+ξ, the Cauchy problem in (23)can be equated to the following expressions:

According to Bellman inequality, the difference between (14) and (15) exists:

Hence ζ(tn|ζtn′) is continuous dependent on the perturbation of the initial point.

Appendix B

Since existing -∞＜E(p)＜0 and 0＜ E(r) ＜+∞, h(ζ) in equation (29) is positive and bounded.

According to (29) and the theorems in the Section 3.1, for two continuous times tnand tn+1, we have:

where K2is an enough constant. As a result, from (31) we can see h(ζ) satisfies Lipschitz condition in the domain of definition＜1. Now relax restriction on ζ to a normal value. For a given enough constant K3=2·max(θMax,K1πMax), we have＜ 1. So ϕm*(ζ)= ϕm*((ζ-d)/K3)is always true. Therefore, we have:

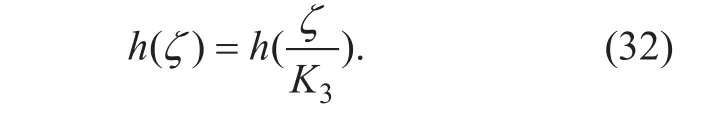
Combining (31) and (32), for the ζ in a normal domain of definition we can get:

Hence h(ζ) is Lipschitz continuous. Then it is easy to learn g(ζ) is also Lipschitz continuous.