六自由度机器人控制器参数的可区分性分析

魏雅慧 杨 超

(1. 三峡大学 大学生素质教育中心， 湖北 宜昌 443002； 2. 三峡大学 电气与新能源学院， 湖北 宜昌 443002)

六自由度机器人，即有6个关节节点，各关节由多轴运动控制器进行独立地伺服控制[1]．闭环系统中的转矩控制、速度控制及位置控制均由伺服控制器完成．为使闭环系统获得较高的动态响应，需要优化系统的驱动特性，即优化控制器的参数，使机电系统达到最佳匹配，从而获得最佳的稳态和动态性能[2]．

由于六自由度机器人控制器的参数众多，优化目标和控制器参数之间的函数关系有时无法直接得到，难以用解析方法进行区分．因此，本文提出一种基于轨迹灵敏度的控制器参数可区分性方法，通过探讨参数是否可被区分，判定参数优化过程中是否存在唯一的最优解．这种分析方法在电力系统动态分析中的应用比较成熟和广泛．在电力系统稳定分析研究方面，主要包括了能量函数法对稳定裕度灵敏度进行计算[3]，网络结构保持下的能量裕度灵敏度计算方法[4]，对单机能量函数下的轨迹灵敏度函数关系的推导，发现快速计算灵敏度和暂态稳定极限的方法[5]．然而在控制系统中，基于轨迹灵敏度的分析方法应用较少，如介绍混合灵敏度控制在电液位置控制系统中的应用[6]，混合灵敏度控制方法在直驱式液压系统中的应用[7]，电动助力转向控制系统基于H∞的混合灵敏度算法[8]．

在实际应用中，包括结构参数及工作参数在内的很多参数都能影响机器人系统的动态特性．灵敏度分析作为一种定量的分析方法，能有效地研究控制器参数对系统动态性能的影响[9-10]．本文通过分析灵敏度曲线的相位，确定不可区分的控制器参数，并以六自由度机器人单个模块控制器为例进行分析，分析结果验证了本文方法的有效性．

1 轨迹灵敏度的计算

轨迹灵敏度定义为当控制器参数发生一定变化时，相应的闭环系统动态轨迹的变化程度，反映了系统轨迹与控制器参数之间的关系．简单地说，轨迹灵敏度是轨迹关于参数的导数，一般应用于非线性系统，且随参数的变化而不同，具有时变性．状态变量或输出变量的轨迹变化对控制器参数的变化率，定义为轨迹灵敏度[11]

yi(K1，…，Kj，…，Km，t)]/ΔKj(1)

式中，yi为系统变量i的轨迹，Kj为系统参数，m为参数总数，t为时间采样点．

为减小由式(1)带来的误差，提高计算精度，故采用中值法计算导数，即分两次计算轨迹：

yi(K1，…，Kj+ΔKj，…，Km，t)

yi(K1，…，Kj-ΔKj，…，Km，t)

然后计算轨迹灵敏度的相对值：

yi(K1，…，Kj，…，Km，t)]/yi0}/(2ΔKj/Kj0) (2)

式中，Kj0为参数Kj的初始值，yi0为参数Kj0的稳态值．

为了对各参数的灵敏度大小进行比较，对于轨迹灵敏度曲线上的各点，取其绝对值的平均值：

(3)

式中N为轨迹灵敏度曲线的总点数．

由此可得：若系统轨迹yi对参数Kj的灵敏度较大，则说明Kj对yi的影响较大，根据yi可以较容易地区分出Kj；反之，若所有的系统轨迹yi对参数Kj的灵敏度都非常小，则说明Kj对所有系统轨迹的影响微小甚至几乎没有影响，Kj不容易被区分．

2 从轨迹灵敏度的角度分析可区分性

在控制器参数的优化整定过程中，该参数是否可被区分的判定标准为该参数能否被唯一确定．设模型中的两个参数分别为Kj、Kj+1，分析系统轨迹可以发现，若Kj、Kj+1不可区分，则说明它们以一种隐函数的关系作用于轨迹[12]，即

y=f[K1，…，φ(Kj+Kj+1)，…，Kn，t] (4)

假设φ(Kj+Kj+1)对两个参数均可导，根据微积分链式规则可得

(5)

则有

(6)

式中，∂y/∂Kj，∂y/∂Kj+1是时变的，而∂φ/∂Kj，∂φ/∂Kj+1是非时变的．因此，在时间轴上轨迹灵敏度∂y/∂Kj，∂y/∂Kj+1互相成比例即在零点处相交，若轨迹灵敏度是振荡曲线，则表现为曲线同相位或反相位．

由上述分析可知，若一些参数的轨迹灵敏度曲线在零点处相交，则这些参数不能被唯一确定，即这几个参数不能被区分．若所有参数的轨迹灵敏度曲线都不在零点处相交，那么所有参数基本上能被唯一确定．

3 单个机器人模块的控制器模型

六自由度机器人的单个运动控制模块相当于一个交流伺服系统，由位置回路、速度回路及电流回路3个反馈回路组成．性能要求如下：1)瞬态响应具有稳定、平滑的特征；2)为获得高精度的位置控制性能，系统需有较小的稳态跟踪误差和动态位置跟踪误差[13]．该系统的控制模型如图1所示．

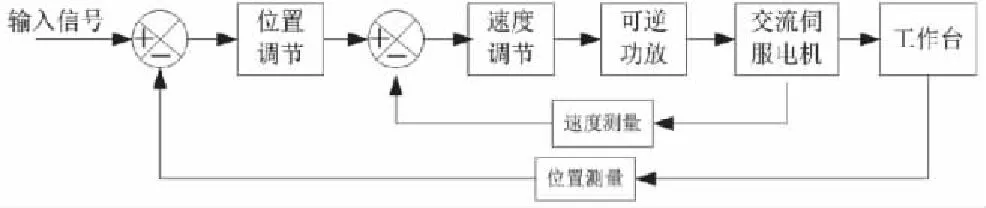
图1 交流伺服系统控制模型

本文采用的交流伺服系统为Ι型系统，对阶跃输入能无静差地复现，但对于其他非阶跃输入，则要经历振荡，为改善系统性能需要进行参数调节和附加控制环节．因此，将系统的伺服放大器、伺服电机及速度测量部分，整体作为伺服控制的调节对象对速度环进行简化，简化后的系统加入比例微分控制，最终得到的系统框图如图2所示．

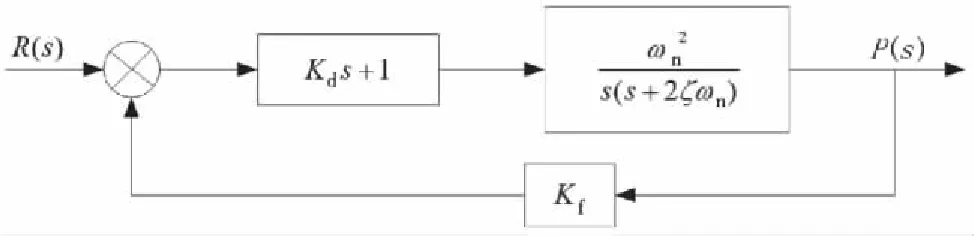
图2 加比例微分控制的交流伺服系统框图

机器人模块等效为一个二阶系统，R(s)为输入位置信号，P(s)为输出位置信号，Kd、Kf分别为PID控制器微分、反馈比例系数．输出位置信号：

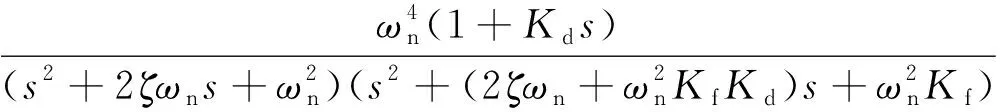
式中，ωn为伺服阻尼自然频率，ζ为伺服阻尼比．

4 单个模块控制器参数的可区分性分析

4.1 算例系统

如图3所示，本文的研究对象为六自由度机器人位置控制系统，其型号为REBot-V-6R，定位精度±0.01 mm，作业半径725 mm，S轴(回旋)动作范围为±170°．该控制系统参数/输入初值见表1．

图3 六自由度机器人

参数/输入ωnζKdKf初值0.2530.7202

以位置输出P为轨迹变量，对应于式(1)中的y．由图2可知，位置系统PID控制器包含2个参数Kd、Kf，对应于式(1)中的K．将这2个控制器参数在其缺省值的基础上，上下变动10%，计算其轨迹灵敏度．表2为2个控制器参数对位置输出P的轨迹灵敏度平均值．由表2可以看出，对于轨迹变量位置输出P，Kf对其影响较大，Kd的影响较小．

表2 机器人控制器参数轨迹灵敏度

4.2 轨迹灵敏度与可区分性

以位置输出P为轨迹变量，PID控制器参数Kd、Kf的轨迹灵敏度曲线如图4所示．从图中可以看出，以轨迹变量P为参考变量，参数Kd、Kf的灵敏度曲线在零点处相交，表现出同相位的特征，说明参数Kd、Kf不能被唯一确定，即它们是不可区分的参数．

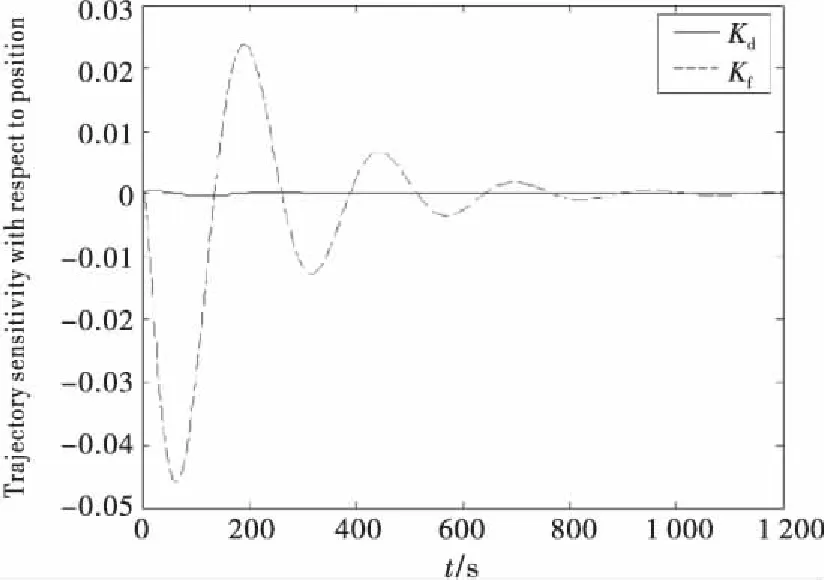
图4 PID控制器参数的轨迹灵敏度曲线

为了对上述结论完成进一步验证，分别对Kd、Kf取不同的参数值，再对轨迹变量P进行Matlab仿真．本文对Kd、Kf的取值组合有3个，如下所示：

①Kd=20，Kf=2；

②Kd=7，Kf=9；

③Kd=6，Kf=8．

其中参数组合①为初值，而参数组合②，③为在使系统稳定的参数区间内任意选取的值．

仿真得到的轨迹动态曲线如图5所示．可见参数组合②，③对应的动态轨迹相差不大，而与参数组合①对应的动态轨迹有较大区别，说明Kd、Kf为不可区分的参数，验证了本文方法的有效性．

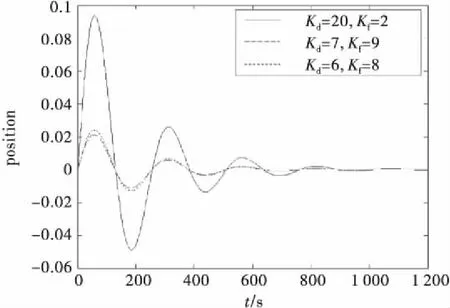
图5 PID控制器参数轨迹变量仿真曲线

5 结 论

本文针对六自由度机器人系统，提出了控制器参数的可区分性问题，即参数的最优解能否被唯一确定．提出了通过分析参数的轨迹灵敏度实现对控制器参数的可区分性的分析，为机器人控制系统参数的可区分性分析提供了新的途径．研究结果表明，若一些参数的轨迹灵敏度曲线相交于零点，则说明它们之间存在相关性，为不可区分参数；若这些参数的轨迹灵敏度都没有在零点处相交，也不存在线性相关的关系，则它们之间不存在相关性，为可以区分的参数．通过对具体算例进行分析，确定了参数Kd、Kf为该六自由度机器人单个模块控制系统中，不能被区分的控制器参数，它们之间存在某种关系，在系统的优化整定过程中无法被唯一确定．因此，为降低控制器优化的维数、提高优化效率，参数Kd、Kf可以取默认值，或者取经过一次优化整定后的值，不必再对其进行继续优化．