基于AGA-GRNN神经网络的刀具寿命预测研究

李浩平 欧阳俊 谢雪媛

(三峡大学 机械与动力学院， 湖北 宜昌 443002)

在回归分析预测刀具寿命的方法中，神经网络方法由于具有较好的非线性逼近能力，能较好地拟合影响刀具寿命的因素与刀具寿命之间的非线性关系，因此得到了广泛使用．大量研究学者运用BP神经网络来实现刀具寿命预测，同时结合GA、ACO、PSO、DE等算法来优化BP神经网络的参数，取得了不错的预测精度和预测效果[1-4]．但是，BP神经网络的网络层数与节点数、神经元之间的连接权值、阈值等参数数量较多，优化工作量较复杂，同时，网络学习速率、传递和训练函数等参数需要人为不断反复调试，才能最终获得预测精度较高的模型，增加了预测模型构建的难度和复杂程度．

针对上述问题，本文提出运用广义回归神经网络(GRNN)来实现刀具寿命预测，与BP网络不同，GRNN学习算法在训练过程中不需要调整神经元之间的连接权值，网络的学习完全取决于数据样本，只需要确定平滑参数，即光滑因子(亦称扩展速度，SPREAD)，且不需要对传递函数、隐含层神经元个数等对模型预测精度和速度产生影响的网络参数进行人为的确定，从而使GRNN预测模型能最大限度地避免人为主观设定对预测结果的影响．同时，分别采用交叉验证法、遗传算法和自适应遗传算法优化网络参数—光滑因子，以提高模型预测的精度和效率．

1 刀具寿命影响因素

实际加工中，刀具寿命通常指刀具从投入使用直到磨钝时的切削时间．通过大量切削实验和实际经验，目前总结出了传统刀具寿命计算公式，见式(1)．

(1)

式中，T为刀具使用寿命，C为与刀具材料、工件材料和切削条件有关的刀具使用寿命修正系数，D为刀具直径，V为切削速度，a为切削宽度，f为每齿进给量，b为切削深度，Z为铣刀齿数；q，x，y，u，p为各个参数对刀具使用寿命的影响系数，数值的大小由专家经验或者试验确定．

2 AGA-GRNN刀具寿命预测模型构建

本文运用广义回归神经网络构建刀具寿命预测模型，在广义回归神经网络中采用自适应遗传算法优化网络模型参数，提高预测精度及效率．广义回归神经网络(GRNN)适用于非线性问题，可以处理不稳定的数据，并在样本数据较少时预测效果也较好[5]．其中，参数σ为高斯函数的宽度系数，在此称为光滑因子．一般采用交叉验证法来确定一个最优值，但耗时长，且精度不高，因此本文采用自适应遗传算法来优化网络的光滑因子．遗传算法(GA)具有群体搜索性、不需要辅助信息、不易陷入局部最优、易于与其他技术混合使用等特点[6]．但一成不变的交叉变异概率影响了算法的效率．因此本文根据个体适应度值而自适应调整交叉、变异概率，以提高算法的效率[7]．

2.1 GRNN神经网络预测模型的构建

GRNN神经网络拓扑结构，如图1所示．

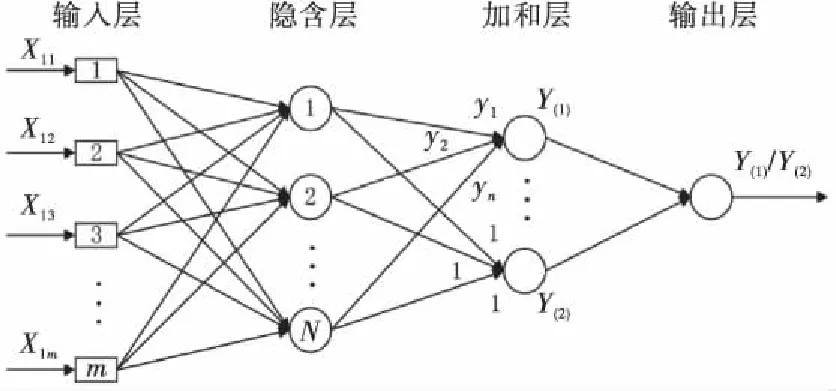
图1 GRNN网络拓扑结构

根据刀具寿命预测的影响因素，可设网络训练样本数量为N，每个样本有m个输入(即m个刀具寿命影响因素)，1个输出(即刀具寿命)．输入向量X=[X1，X2，…，XN]T，其中Xj=[xj1，xj2，…，xjm]，j∈[1，N]，其期望输出为Y=[y1，y2，…，yN]T．

1)输入层神经元个数等于单个样本输入的维数m，其传输函数是简单的线性函数；

2)隐含层神经元个数等于训练样本个数N，第i个神经元的中心向量为Xi，隐含层每个神经元对应一个期望输出yi，一个实际输出fi(σ)，其中σ为网络光滑因子，其基函数为高斯函数；

3)加和层中第一类神经元计算隐含层神经元的加权和，权值为各训练样本的期望输出值，其加权和输出为

(2)

加和层中第二类神经元计算隐含层神经元的代数和，其代数和输出为

(3)

2.2 自适应遗传算法优化GRNN神经网络

本文采用AGA算法来优化GRNN网络的光滑因子，构建AGA-GRNN神经网络，具体步骤如下．

1)遗传算法初始化，在光滑因子σ可能的取值搜索范围[σmin，σmax]内，随机生成规模为NIND的初始种群P(g)，采用实数编码，确定遗传算法选择概率、最大遗传代数等参数，进化代数g=0；

2)建立遗传算法的适应度函数．本文采用的适用度函数为GRNN神经网络的预测值与实际值的误差的平方之和的倒数，作为评价种群中个体适应度函数．适应度越大，表明个体越优良．适应度函数见式(4)；

(4)

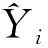
3)选择．将初始种群P(g)按照个体适应度大小进行选择，其第j个个体被选择保留的概率pj公式见式(5)；

(5)

4)交叉、变异．将选择保留的个体进行交叉、变异，在交叉概率pc和变异概率pm的调整上，引入自适应机制，使pc、pm将随着个体适应度值的变化而自适应地改变，其自适应调整公式见式(6)、(7)，最后得到新的种群P(g+1)，进化代数g=g+1；

(6)

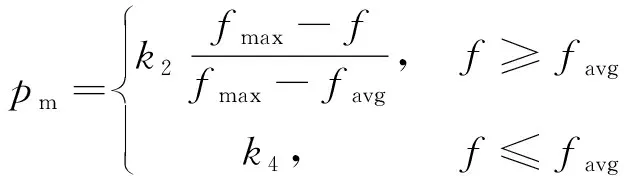
其中，f′为要交叉的两个个体中较大的适应值；f为变异的父个体适应值；fmax为种群个体的最大适应值；favg为种群的平均适应值；固定参数k1=0.5，k2=0.02，k3=0.85，k4=0.05；

5)判断进化代数g是否达到最大进化代数，若达到则计算结束，返回当前适应度最高的个体；否则转至步骤(2)，直到满足终止条件；

6)以最优光滑因子σ值作为GRNN网络模型的参数，建立刀具寿命预测模型；

7)计算预测结果，评估GA-GRNN网络性能．

3 实例预测结果及分析

3.1 原始数据预处理

以文献[8]中的实验数据作为本文预测模型的原始数据，来验证本文所建刀具预测模型的有效性．实验样本采用工件材料为45钢、刀具材料为硬质合金立铣刀、加工方式和要求为立铣和粗铣．因为实验中工件材料、刀具材料和加工方式是确定的，因此考虑的刀具寿命影响因素为6种，通过试验选取表1所示的10组样本数据，其刀具寿命为利用传统的刀具寿命经验计算公式(1)计算得到的期望值．将数据编号1～7组试验样本数据作为刀具寿命预测的训练样本，编号8～10组试验样本数据作为检验预测模型推广能力和有效性的校验样本．

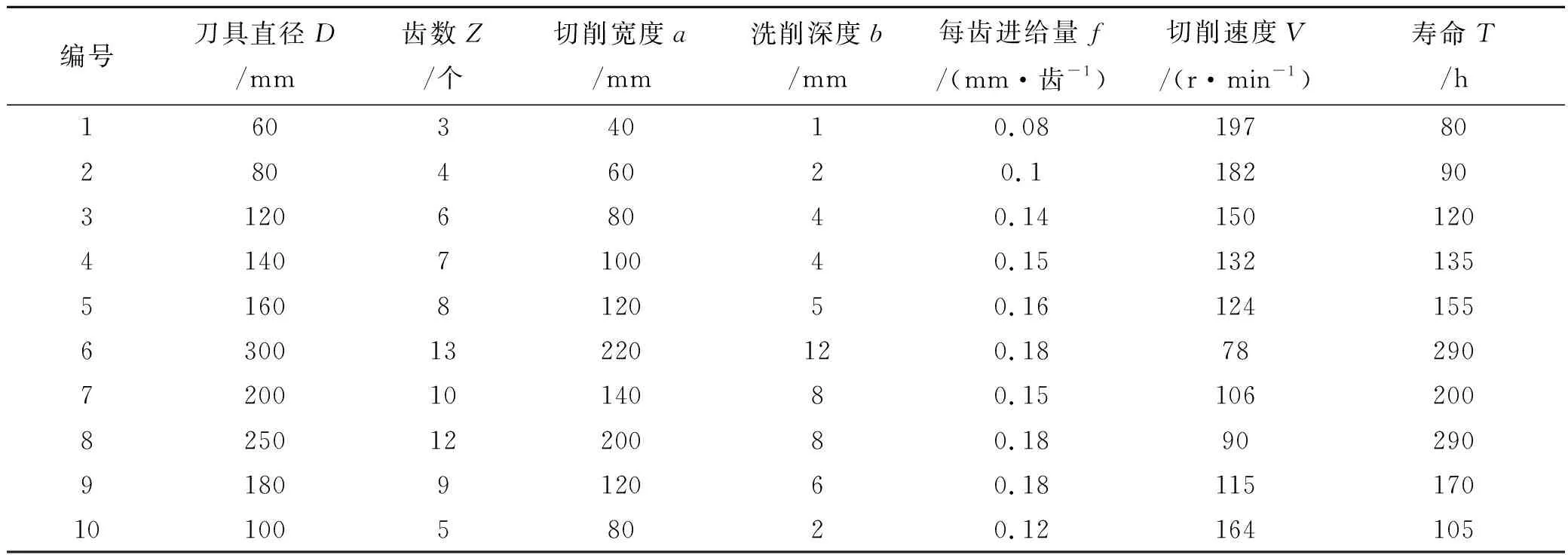
表1 刀具寿命原始样本

运用神经网络建模时，往往根据实际情况选择原始数据的处理方式，本文在运用AGA-GRNN神经网络和交叉验证法GRNN神经网络下，采用原始数据不处理、数据归一化至[-1,1]和数据归一化至[0.1,0.9]的3种方式来进行原始数据的预处理，对比不同预测模型、不同数据处理方式下的预测结果精度，具体结果见表2．

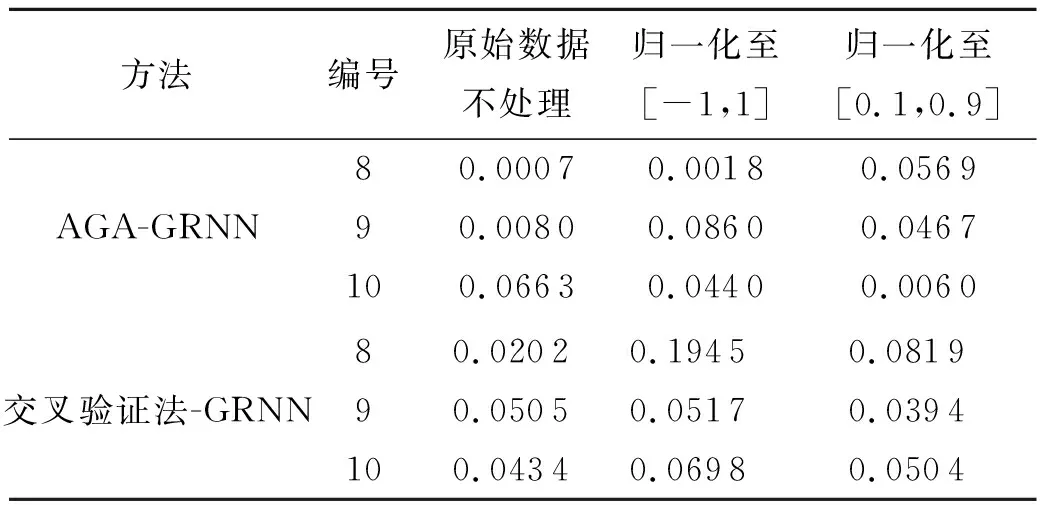
表2 各数据处理方式下的预测结果误差

根据表2所示，在运用AGA-GRNN神经网络和交叉验证法GRNN神经网络预测模型下，当模型输入数据采用原始数据时，其预测误差均小于归一化处理后的输入数据．由此可见，在运用广义回归神经网络实现刀具寿命预测时，采用原始数据作为输入数据能够获得更高的预测精度．

3.2 光滑因子优化结果分析

采用3种方法对光滑因子进行了优化：AGA算法、GA算法和交叉验证法．

在运用AGA算法优化光滑因子时，初始种群规模为30，进化代数为50，选择概率为0.9，交叉和变异概率根据种群适应度值自适应调整，光滑因子搜索范围为[0，50]．同时与GA算法优化光滑因子过程进行对比，通过模拟得到遗传算法过程中解的目标函数均值及解的变化曲线，如图2～3所示．显然，AGA算法相较GA算法收敛速度更快．

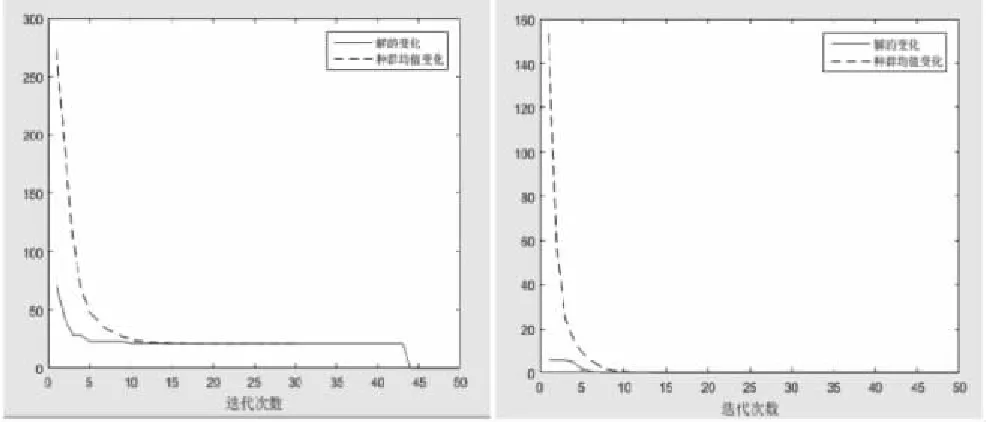
图2 GA优化解的种群目标 图3 AGA优化解的目标函数函数均值及解的变化曲线 均值及解的变化曲线

此外，还与交叉验证法优化光滑因子方法在寻优效率上进行了对比，交叉验证法中，设置光滑因子按照固定的增量Δ=0.1，在一定的范围[0，50]内递增．

光滑因子优化效率见表3，可见运用AGA算法在运行时间上均少于GA算法和交叉验证法，光滑因子寻优效率显著提高．

表3 光滑因子优化效率对比

3.3 刀具寿命预测结果分析

直接采用原始数据作为模型输入数据，先采用编号1～7组训练样本分别训练AGA-GRNN神经网络、交叉验证GRNN网络和GA-GRNN网络，再对编号8～10组试验样本进行预测，预测结果见表4，预测结果相对平均误差如图4所示．

表4 预测结果对比

图4 预测相对平均误差对比图

通过上述结果对比图表可知，模型预测精度由高到低依次为：AGA-GRNN神经网络模型、GA-GRNN神经网络模型、交叉验证GRNN神经网络模型．在光滑因子寻优方面，相较交叉验证法，AGA算法不仅降低了预测平均相对误差，同时，网络效率大大提高．因此，本文运用AGA-GRNN神经网络取得了较好的预测效果．

4 结 论

针对运用BP神经网络预测刀具寿命方法存在的网络需要优化参数较多，计算量偏大，减少人为主观设置网络参数值对预测结果的影响，本文提出的自适应遗传算法优化广义回归神经网络的刀具寿命预测方法取得了不错的预测效果，结论如下：

1)实例结果表明，在运用广义回归神经网络预测刀具寿命时，相较针对原始数据归一化处理，直接采用原始数据作为网络模型的输入数据，预测结果精度更高．

2)AGA-GRNN刀具寿命预测模型在参数优化效率和寿命预测精度上均高于另外2种模型，具有一定的理论意义和实用价值，此刀具寿命预测模型的构建为实现制造系统中智能刀具调度提供了基础．