三招“搞定”数量积

雷亚庆

有些同学在解决相对复杂的数量积问题时感觉无从下手，实际上只要掌握好三“招”，即可轻松搞定数量积问题.

[第一招]自乘（定义法：直接利用向量数量积公式）

所谓自乘，就是指利用向量数量积的定义，即利用α·b=|α||b|cosθ直接计算，这类问题是求数量积问题中比较简单和基础的.

[第二招]它乘（基底法：转化为其他向量的数量积）

它乘，又称基底法，是指利用平面向量基本定理把所求向量用两个不共线已知模长和夹角的向量或具有特殊位置关系（主要指垂直）的向量来线性表示，从而把所求向量的数量积转化为两个已知向量的数量积，从而使问题得以解决。

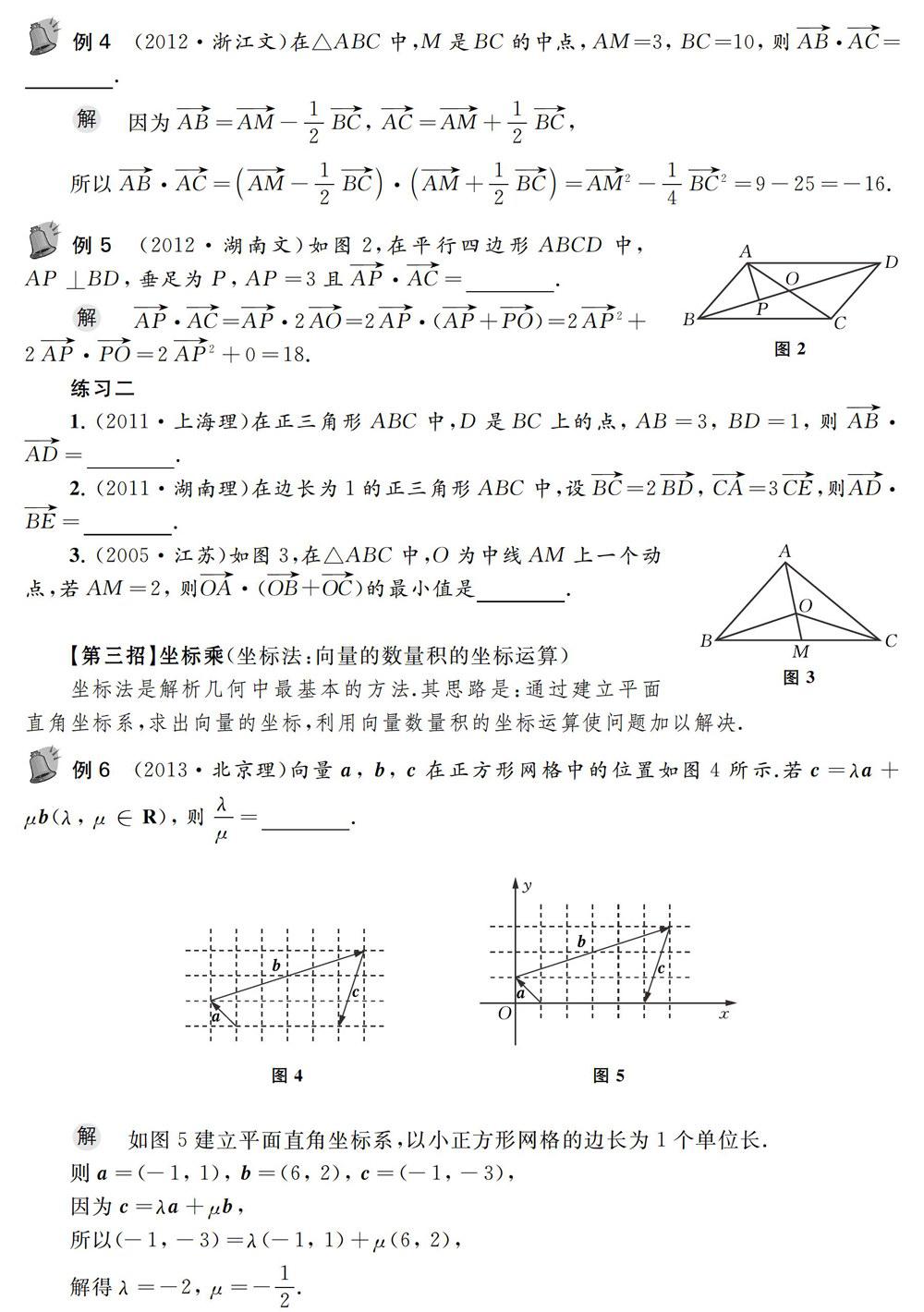
[第三招]坐标乘（坐标法：向量的数量积的坐标运算）

坐标法是解析几何中最基本的方法，其思路是：通过建立平面直角坐标系，求出向量的坐标，利用向量数量积的坐标运算使问题加以解决.

向量数量积是高考中的重点和热点，因为它是联系代数与几何的工具，所以同学们一定要熟练掌握求数量积的方法.有了这三招，相信同學们一定可以轻松“搞定”数量积问题.