吃透“两头” 精准“制导”——以《认识周长》备课为例

林 俊（特级教师）

关于教师如何备课，最通俗、最简洁的说法是吃透“两头”，即吃透教材、吃透学生。笔者发现：教师在吃透教材上，花的功夫要比吃透学生多得多；对于吃透学生，我们做得还远远不够。那么，如何落实好吃透“两头”呢？下面以《认识周长》教学为例谈谈具体做法。

【教材解析】

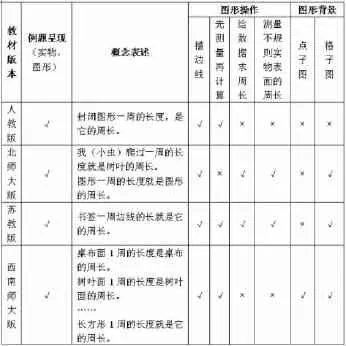
《认识周长》国内各个版本均安排在三年级上学期教学。不同版本的教材，编排的侧重点也是有差异的。现以人教版、北师大版、苏教版和西南师大版为例，从例题呈现、概念表述、图形操作、图形背景等方面比较如下。

?

可以看出，各种版本教材在“例题呈现”时，都能兼顾到实物与图形并重，从学生熟悉的具体实物开始感知，逐步过渡到抽象的图形认识，使学生不仅对周长的概念有完整的认识，也促进学生在习得周长概念的同时，实现思维同步从具象到抽象的转化、提升。

【学情调查】

教材编排有差异，我们是选择其一，还是兼收并蓄？理智的选择当然是博采众长。那么，该如何取舍？这时，我们不要忘了备课的另一头——学生。学生的学情是决定内容取舍、方法选择的重要依据。于是，我对教学班级的41名学生进行了全员问卷调查。期望通过调查，探明学生的底细，使教学有的放矢，精确“制导”。前测结果如下：

1.“听说过‘周长’这个词”的有15人，占36.6%，约占三分之一；没有听说过的26人，占63.4%，约占三分之二。

2.能够正确描出封闭图形一周边线的有29人，占70.7%；把不封闭图形也描上的有18人，占43.9%。

3.根据图形每条边的长度，计算图形的周长。有27人能够正确计算（主要用加法），占65.9%，约占三分之二。

4.对于“如何知道长方形一周的长度”，100%的学生知道需要测量长方形每条边的长度，并且能够准确测量，但是只有53.7%的学生知道还要把测量出来的长方形各边长度相加。

对于圆，学生基本上想不出什么办法测量。只有三位学生的想法靠谱一点：手指宽为1厘米，手指在圆上面绕一圈，绕多少下就是几厘米；用一个类似的圆在上面画好几厘米再量；用一根线围一个圆（要一样大），再把线拉直了量。

5.在方格纸上画一周的长度是12厘米的图形情况：一个图形也画不正确的有22人，占53.6%，画出一个图形的有8人，占19.5%，画出两个图形的有9人，占22.0%，画出三个图形的有2人，占4.9%。而且只有一位学生能够画出变式图形，其他学生画出的都是长方形或正方形。

根据以上测试，我们得出以下结论：大约三分之一的学生对周长有一些了解，但对周长的意义的把握还要厘清、匡正、完善。七成学生对“边线”能够理解，但有近一半学生对图形是否封闭缺乏认知。

测量直边图形的边长没有问题，但有超过一半的学生需要学习周长的算法。对于测量曲边图形的周长，学生基本想不出“化曲为直”的方法。

在方格纸上设计指定周长的图形，一半多的学生不会设计。即使学生设计出来的图形，基本上也是常见的长方形、正方形等基本图形，变式图形极为罕见。

【教学过程】

一、活动引入，直奔主题

（出示两张教师的照片，一张是几年前的，一张是近期的）

师：大家看到这两张照片，有什么想说的吗？

生：老师变胖了！

师：你的眼力真好。我感觉最明显是这个地方变粗了（指腰部），也就是腰围变大了。哪位同学来量量老师的腰围？

生：（看着米尺）不是这种尺，应该用软尺。

（提供软尺，该学生测量）

师：腰围是什么意思？

（出示测量腰围的照片）

生（众）：腰一周的长度。（板书：一周的长度）

师：这里“周”是什么意思？“长”呢？

生（众）：“周”是一周、一圈的意思，“长”是长度的意思。

二、活动推进，内化概念

●活动1：认识物体表面的周长。

1.指一周。

师：（出示数学书）你能指出数学书封面一周的长度吗？

（学生上前指：从一点出发，绕一周又回到起点）

师：告诉大家，指的时候要注意什么？

生：从一个点沿着边线开始，最后又回到这一点。

师：谁能从不同的地方开始也指出数学书的一周呢？

（另一个学生从不同的地方开始，指出了数学书封面的一周）

师：（指着书边线上的一点）如果从这儿开始，到哪儿结束？

生：还是到这个点结束。

师：也就是从哪儿开始——

生（众）：到哪儿结束。

师：这样就构成了一周。

师：（出示一片树叶）这个物体有点怪，请你指出它表面一周的长度。

2.找一周。

师：生活中，许多物体的表面都有一周。下面我们一起来找一找，然后同桌两人互相指一指、说一说：这是（ ）表面一周的长度。

3.比一周。

师：找到的这些物体中，哪些物体表面一周的长度比课桌面一周的长度短？哪些比它长？

生：黑板面的一周、屏幕面的一周比课桌面一周的长度长，数学书封面的一周、直尺面的一周比课桌面一周的长度短。

师：看来同样是物体表面的一周，但是这一周却有的长、有的短。我们就把物体表面一周的长度叫做物体表面的周长。（板书：物体表面）

4.说一周。

师：现在，我们就可以这样说——

数学书封面一周的长度，是（ ）；课桌表面一周的长度，是（ ）；树叶表面一周的长度，是（ ）；（ ）是黑板面的周长；（ ）是直尺面的周长。

师：像这样说得完吗？

生：说不完的。（出示：……）

师：的确，千言万语也说不完，你能用一句话把大家已经说的和没有说的都一网打尽吗？［出示句式：（ ）是（ ）的周长，让学生思考］

生：什么物体一周的长度，就是什么物体的周长。

师：你的意思是物体表面一周的长度，是物体表面的周长。简单一点说，物体表面一周的长度，是它的周长。（课件出示这句话）

●活动2：认识封闭图形的周长。

1.游戏。

师：刚才我们从指数学书封面一周的长度开始，认识了物体表面的周长。（课件出示数学书封面图片）如果把这一周描下来，就是一个长方形。（课件去除数学书封面图片，留下长方形）谁来指出它的周长？

师：是不是所有的图形都有一周的长度呢？

（学生有的说“是”，有的说“不是”）

师：我们来看几个图形（出示下图）。

① ② ③ ④师：选择其中一个图形，描出它一周的长度，限时10秒。

师：你描的几号图形用手势表示出来。

师：你为什么不描③号图形？

生：③号图形是开口的、断开的。如果从一个起点出发，回不到起点。

师：像角这样开口的图形叫做不封闭图形，（课件去掉图③，指着剩下的图形）这些图形叫做封闭图形。（板书：封闭图形）

师：这些都是封闭图形，为什么大多数同学都描了②号图形？

生：因为它一周的长度最短。

师：看来，封闭图形一周的长度，也是有的长有的短，那什么是封闭图形的周长呢？

生：封闭图形一周的长度，是它的周长。

2.概括。

师：到此为止，我们知道了——还知道了——连起来说就是——物体表面一周的长度叫做它的周长，或封闭图形一周的长度是它的周长。这两句话有些词重复，合成一句话怎么说？

生：物体表面或封闭图形一周的长度，是它们的周长。

后测效果：“周长”什么意思？36人给出一句话表达，占87.8%，意思准确、到位。能够正确描出封闭图形一周边线的有41人，占100%；把不封闭图形也描上的只有3人，占7.3%。说明绝大部分学生能够理解周长概念的内涵。

3.测量。

师：我们已经知道②号图形周长最短，周长最长的是几号图形？

生：①号、④号。

师：要知道哪个图形周长最长，最长的比最短的长多少？怎么办？

生：量出这几个图形的周长。

师：那就请你量一量、算一算。

（量的过程中，学生遇到了圆不可以用直尺量的问题）

师：先把前面两个图形的周长量一量、算一算。

［师生共同核对①②两个图形的测量数据和有关算式，长方形周长：3+3+2+2=10（厘米），正方形周长：1+1+1+1=4（厘米），学生自我对照、批改］

师：圆的周长不方便用直尺直接量，怎么办？

生：用软尺量。

师：如果没有软尺，只有直尺怎么办？哪个小组介绍一下你们的方法？

生：用一个类似的圆在上面画好几厘米再量。

师：还有什么办法？

（学生想不出来，教师让学生取出“锦囊”——信封内有一枚一元硬币、一根细铁丝和一根细毛线）

生：先用细毛线绕硬币围一圈，做好记号，再把细毛线拉直，测量细毛线的长度就可以。

生：用细铁丝也可以。

师：（播放用细毛线量树叶周长的视频，播放过程中教师适时介绍操作要领）现在大家想不想自己动手测量这个一元硬币的周长？（出示活动建议，小组活动）活动建议：

1.选择其中一种或两种材料。2.可以围一围、量一量。

3.还有其他测量方法吗？

（学生分组测量，两分钟后，请一组学生上来演示测量一元硬币的过程）

师：回过头来看一看，哪个图形周长最长？

生：长方形周长10厘米，圆周长约8厘米，长方形的周长最长。

师：最长的比最短的周长长几厘米？生：10-4=6（厘米）。

师：还有其他测量方法吗？

（课件播放硬币滚动一周测量周长的视频）

师：这种方法要注意什么？

生：先在要测量的圆片上做一个记号，再把圆片在尺上滚一圈。

师：什么时候用直尺直接量？什么时候用软尺或先借助线来量？

生：边是直的用直尺直接量，边是弯的用软尺或先借助线来量。

师：（小结）直边图形可以用直尺先量再算，曲边图形可以用软尺直接量，也可以借助线先围再量。（板书：直——直尺；曲——软尺量、线）

后测效果：有39人能够正确“计算下面各图形的周长”（主要用加法），占95.1%，只有2人列对算式，计算出错，占4.9%。说明原来教材编排的“先测量再计算”“根据给出的数据，求图形的周长”，这些要求确实低于绝大部分学生的数学现实。

对于“你有什么方法知道下面每个图形（长方形、圆）一周的长度？请把你的想法写下来。”

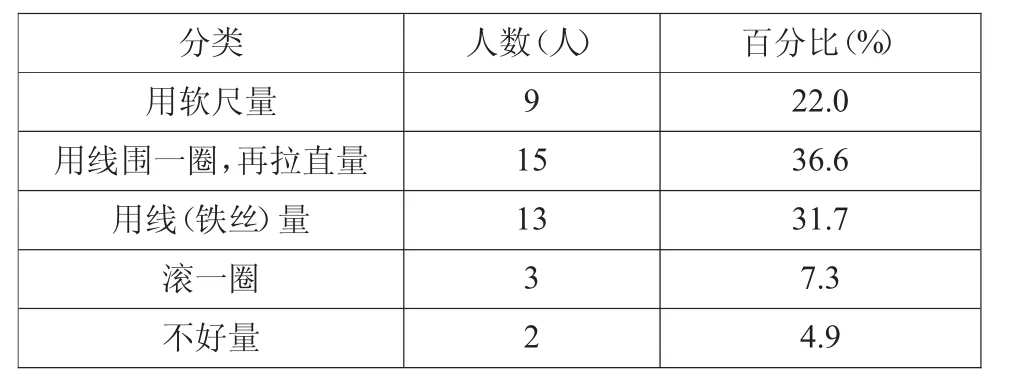
100%的学生知道需要测量长方形每条边的长度，再把测量出来的长方形各边长度相加。其中80.5%的学生准确测量了长方形每条边的长度，但是还有12.2%的学生没有把测量出来的长方形各边长度相加。对于圆，出现了多样化的方法，如下：

分类 人数（人） 百分比（%）用软尺量 9 22.0用线围一圈，再拉直量 15 36.6用线（铁丝）量 13 31.7滚一圈 3 7.3不好量 2 4.9

95.1%的学生给出了至少一种方法，只有4.9%的学生没有掌握测量曲边图形周长的方法。

●活动3：在方格纸上画一个周长是12厘米的图形。

挑战指数：

★★★ 画出一个图形；

★★★★ 画出两个形状不一样的图形；

★★★★★ 画出的图形有创意。

师：（展示学生图形一）周长是12厘米吗？

图形一

师：（展示学生图形二）符合要求吗？

图形二

师：（展示学生图形三）这个呢？

图形三

师：从图形一、二、三看出周长是12厘米的图形，可能是长方形，还可能是——

生（齐）：正方形。

师：还可能是其他形状吗？这个图形的周长还是12厘米吗？我们一起数一数。

生（众）：1、2……12，是12厘米。

师：这两个图形有什么相同的地方？又有什么不同的地方？

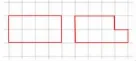
生：它们的形状不一样但周长都是12厘米。

师：你能把左图变成右图吗？

师：下面这两个图形的周长都是12厘米吗？

生：是的。

师：（课件出示若干个长4厘米、宽2厘米的长方形）这些长方形还可以变成什么图形？

师：这是从右边的角开始，慢慢缩进一格、两格、三格。周长变化了吗？

生：没有。

师：这是分别从左边、右边的角开始，慢慢缩进一格、两格的。周长变化了吗？

生（众）：也没有。

师：还可以怎样变化？

生：缩进三个角。

师：（课件继续动态演示）这是分别从对角开始，慢慢缩进一格、两格的。周长变化了吗？

生（众）：还是没有。

师：长方形可以变化成这么多的图形，那么正方形呢？有兴趣的同学，请课后思考。

后测效果：对于问题“请在方格纸上画一周的长度是12厘米的图形。（至少画两个，尽量画不同的图）”无论画出的图形个数还是图形的变式情况，学生的表现都超出了我们的想象，具体情况如下。

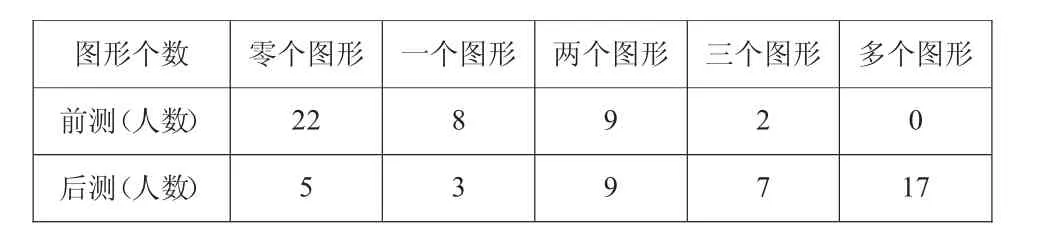
图形个数 零个图形 一个图形 两个图形 三个图形 多个图形前测（人数） 22 8 9 2 0后测（人数） 5 3 9 7 17

能够画出变式图形有29人，占70.7%，而前测只有1人，具体如下：

图形矩形矩形变式 既有矩形又有矩形变式 其它特殊变式 没有画正确人数 7 4 16 9 5

三、活动回顾，总结学法

师：今天学习了什么？

生：周长、测量方法。

师：什么叫做周长？

生：物体表面或封闭图形一周的长度，是它们的周长。

师：测量周长的方法有哪些？

生：量、围。

师：你们有什么要问的吗？

（如果学生提不出，教师给出问题：学习周长的知识有什么用？课件依次出示相关图片：配画框、装修房子用踢脚线、窗户密封条等，用料多少，需要知道它们的周长）