一种高分辨率光栅光谱仪的光路设计

陈 凯, 庞亚军, 周克燕

(1.天津市德力电子仪器有限公司, 天津 300380;2.天津大学光电信息技术教育部重点实验室, 天津 300072)

引 言

在光纤通信领域，各种半导体激光光源、光纤放大器、滤波器等有源或无源器件的应用日益广泛，而波分复用技术的发展使得光信道间隔越来越密集，这就导致光信号在信道中传输的情况更加复杂[1-3]。因此，无论是光纤通信系统研究机构、器件生产厂家还是运营维护机构，都需要对光信号的光谱进行探测，充分了解光源质量和经过光纤通信系统后的光信号品质，以保证光纤通信系统的性能[4-5]。测量光谱最理想的仪器是光谱仪[6-8]，但是，目前国内光纤通信系统领域使用的光谱仪被国外垄断，其主要厂家有美国EXFO、安捷伦、日本横河等，无国产商业化产品。

光栅光谱仪是光纤通信系统测试的主流光谱仪，其光栅分光在波长范围、分辨率和成本等方面能够满足光纤通信系统波段的测试需求。目前光纤通信所用光栅光谱仪主要采用双通结构，即两次衍射分光系统来达到较高的分辨率，通过旋转光栅进行波长扫描，典型的如安捷伦公司的双通光路结构和中国电子科技集团41所的准Littrow光路系统等[9-12]，见表1。

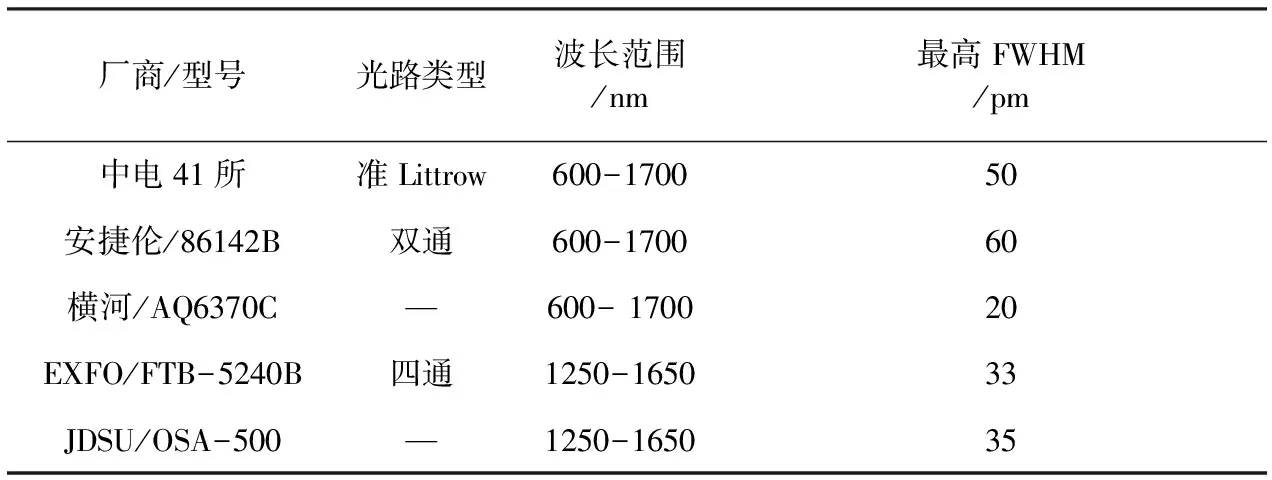
表1 国内外光纤通信光栅光谱仪现状

从表1可知，目前国内外光纤通信光栅光谱仪的光谱分辨率(FWHM)在60 pm～20 pm之间，光路中准直系统采用焦距为百毫米级别的球面镜，因此设备结构复杂，体积大，成本高，对调试要求很高[13-14]。另外，大焦距的准直系统会因振动或者温度变化而引起接收光斑位置漂移，使得接收狭缝需要有机械对准系统，这再次增加了系统复杂性和成本。

针对这一现状，本文设计了一种新型光栅光谱仪结构，其特点是使用直角棱镜和平面镜对衍射光束进行多次反射，使光束四次达到光栅表面进行衍射，得到了高于双通光路的分辨率效果。该光路设计采用了常见的光学器件，准直器件的焦距更短，调试部件少，得到了性能优良、成本低的良好效果。新设计为国内高分辨率光栅光谱仪的发展提供了重要的发展思路。

1 光路基本原理

根据光栅衍射理论，光栅的色分辨效果正比于光谱级次和光栅线数[15]。受多种因素限制，光谱仪光路中不宜采用高级次或增加光栅线数的办法来提高分辨率。本文提出的思路是通过增加衍射次数的办法(等效于提高了光栅线数)，来达到提高分辨率的目的，光路设计如图1所示。

图1 高分辨率光谱仪的光路原理示意图

图1中，FA为两芯单模光纤阵列(Fiber Array)，两光纤端面作为出射与代表入射狭缝，狭缝宽度是单模光纤芯层直径，约9 μm；LEN为消色差透镜(Achromatic Len)，焦距50 mm；AD为消色差消偏器(Achromatic Depolarizer)，可消除偏振对光栅衍射效率的影响；G为全息平面光栅(Grating)，光栅常数为900 g/mm；P为直角棱镜(Right Angle Prism)，系统设置1700 nm时入射角为75°，此时衍射光宽度最宽，因此直角棱镜应固定于长边垂直于1700 nm衍射光的位置；M为平面反射镜(Mirror)。

新型光路的工作原理是：待测信号通过FA的一根纤芯(入射狭缝)导入，经过消色差透镜变为平行光，使得光信号偏振度降低，同时光束第一次入射到光栅上，被衍射分光；垂直入射棱镜的衍射光被棱镜折反后第二次入射到光栅上，第二次衍射光照射到平面反射镜后被垂直反射回光栅，形成第三次衍射；第三次衍射光被棱镜再次折返后第四次照射到光栅上，第四次衍射光又透过消色差消偏器被透镜聚焦至FA的另一个光纤端面(出射狭缝)，完成分光过程。通过旋转光栅，使得不同波长衍射光依次垂直入射到直接棱镜上，而只有垂直入射的光才能聚焦到出射狭缝中，从而完成光谱扫描过程。

2 光学系统分析

2.1 衍射理论

光栅四次衍射的等效衍射光路如图2所示。

图2 四次衍射的等效衍射光路

假设λ0为二面角反射棱镜处于当前位置时被选择的波长，λ0+Δλ为另外一个与其相差Δλ的波长。当待测光被光栅第一次衍射时，两个光束分别满足下面的光栅衍射方程：

d(sinα1+sinβ1)=mλ0

(1)

d[sinα1+sin(β1+Δβ1)]=m(λ0+Δλ)

(2)

式中，α1为待测光的入射角；β1和β1+Δβ1分别为波长λ0和波长λ0+Δλ的第一次衍射角；Δβ1为两波长第一次衍射光的夹角；m为衍射级次，值为1。

待测光经过第一次光栅衍射后，λ0会垂直入射二面角反射棱镜，并被原路反射回来。而λ0+Δλ的光束在被第二次衍射前始终与λ0有Δβ1的夹角，再次入射光栅进行第二次衍射时，波长λ0和λ0+Δλ分别满足以下光栅方程：

d(sinβ1+sinα1)=λ0

(3)

d[sin(β1-Δβ1)+sin(α1+Δβ2)]=

(λ0+Δλ)

(4)

式中，Δβ2为两个波长第二次衍射光之间的夹角。

之后，波长为λ0的光束被平面反射镜原路返回，再次以入射角α1入射光栅发生第三次衍射，而波长为λ0+Δλ的光束则以入射角α1-Δβ2发生衍射，因此第三次衍射中两束光分别满足从下光栅方程：

d(sinα1+sinβ1)=λ0

(5)

d[sin(α1-Δβ2)+sin(β1+Δβ3)]=

λ0+Δλ

(6)

式中，Δβ3为两个波长第三次衍射光之间的夹角。

第三次衍射后，波长λ0再次被二面角反射棱镜原路反射回，以入射角β1入射光栅进行第四次衍射，而波长λ0+Δλ则以入射角β1-Δβ3入射。之后，波长λ0将会按原来的入射角α1衍射，然后被双胶合透镜聚焦到出射光线端面。因此，第四次衍射中两束光分别满足光栅方程：

d(sinβ1+sinα1)=λ0

(7)

d[sin(β1-Δβ3)+sin(α1+Δβ4)]=

λ0+Δλ

(8)

式中Δβ4为两波长第三次衍射后衍射光之间的夹角。

对于小角度Δβ1、Δβ2、Δβ3和Δβ4，可做如下近似：sinΔβ1=Δβ1,cosΔβ1=1；sinΔβ2=Δβ2,cosΔβ2=1；sinΔβ3=Δβ3，cosΔβ3=1；sinΔβ4=Δβ4，cosΔβ4=1。联立式(1)、(2)、(4)、(6)和(8)可得四次色散公式(9)与(10)：

(9)

(10)

式中f为消色差透镜焦距。

2.2 波长与入射角关系

新系统设置1700 nm时的入射角为75°，根据式(1)得衍射角为34.338°，此时入射光与该衍射角的差值为A=75°-34.33°=40.662°，因此只有当经过透镜准直的平行光与某一波长的衍射光夹角为A时，该衍射光才能垂直入射到棱镜中，最终聚焦到出射狭缝，因此：

α1-β1=A

(11)

与光栅方程式(1)联立得：

(12)

由此得到了旋转光栅的波长与入射角的关系。

3 仿真分析

使用Zemax软件对四次衍射光路进行仿真模拟，如图3所示。

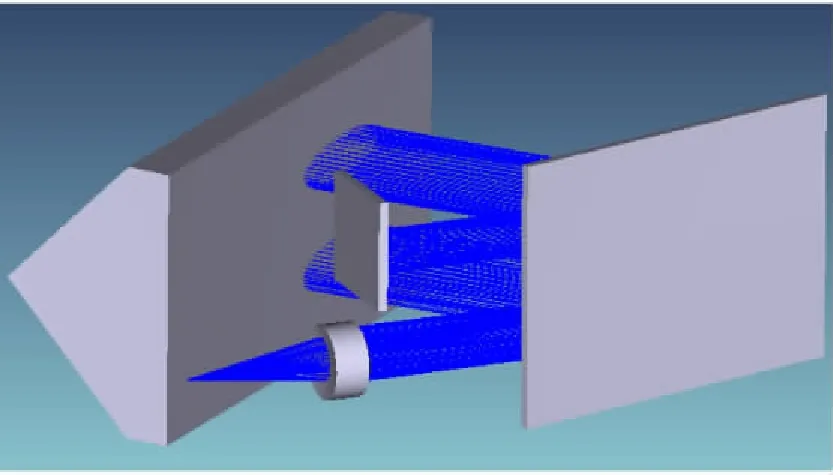
图3 Zemax光路仿真

绘制了与中心波长600 nm，1310 nm，1550 nm和1700 nm相距20 pm的点列图，如图4所示，图中圆圈为艾里斑直径。

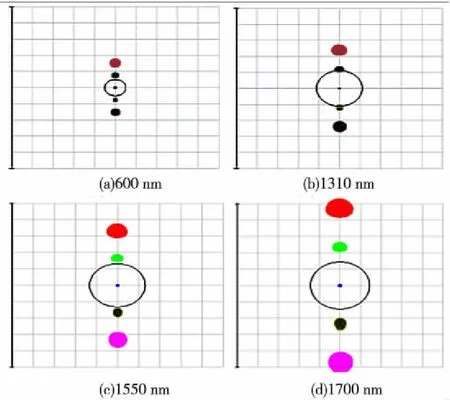
图4 点列图

联立式(10) 与(12)，得到600 nm-1700 nm范围与20 pm波长的间隔距离，如图5所示。

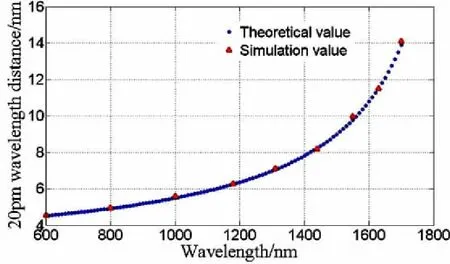
图5 20 pm波长间隔距离

从图4和图5可知，新光路设计可将20 pm波长间隔很好地分离，且波长越长线色散越大，波长分离距离也就越大，由此说明仿真结果与理论计算符合。

4 分辨力分析

光谱仪光路分辨力由多种因素决定，最主要限制因素是艾里斑直径与接收狭缝宽度。从图3可知，从600 nm～1700 nm，艾里斑直径均小于20 pm波长间距。由于接收狭缝为两芯单模光纤阵列中的一根光纤端面芯层，直径D约为9 um，代入(10)式，则该光路的光谱分辨力为[16-17]：

(13)

与(12)式联立得波长与分辨力关系，由此绘制的分辨力曲线如图6所示。

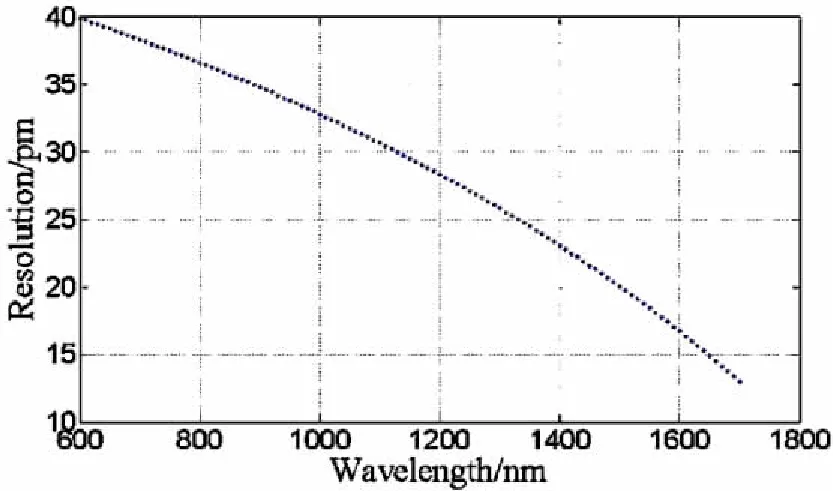
图6 分辨力曲线

从图6可知，新光路设计能够满足600 nm～1700 nm波段的分光，分辨力随波长变化，波长越大分辨力越小，波长大于1510 nm时分辨力大于20 pm，而在1700 nm处时达到的最大分辨力为13 pm。

5 结 论

(1)设计了基于光栅四次衍射的光纤通信用光谱仪光路，采用光纤阵列作为出射和入射狭缝、消色差透镜与消色差消偏器作为准直和消偏器件、光栅分光、直角棱镜与平面镜进行反射和衍射光。新光路设计通过实现四次衍射来提高分辨率，同时减小光路体积，降低调试难度。

(2)通过理论分析得到了新光路光栅进行四次衍射的分辨率方程，同时进行了仿真模拟，理论计算与仿真结果相符，均表明新光路设计能够应用于光纤通信600 nm～1700 nm波段的分光，分辨力达到了C波段的20 pm，1700 nm处的分辨力为13 pm，可实现对光谱的高分辨率探测。