海面风的短期预测和分析
2018-11-22屈春晓任久春朱谦
屈春晓, 任久春, 朱谦
(复旦大学 信息科学与工程学院, 上海 200433)
0 引言
本文的研究背景主要是基于风对帆船运动的影响。帆船运动是人与自然完美结合的体育竟技项目。以自然风作为原动力,运动员根据风和流的实际情况选择航线,通过操控风帆和调整姿态来驾驶船只前行。因此在帆船比赛中,风速风向的准确预测可以使得运动员提前做好姿态调整和心理准备,对于整体的赛前战术也有很强的指导意义。
本文采用了帆船比赛场地的实地数据来进行建模仿真,用时间序列分析法对原始风速风向数据做了一步和多步短期预测,为了提高精确度,后续还利用卡尔曼滤波法进行进一步的预测分析。实例表明融合法有效的提高了预测精度。最后还将预测的数据进行数据分析,以图表的形式直观的展现出来,突出该时间段内海面环境的特征,有助于运动员的训练和比赛。
因为数据预测和分析需要在运动员比赛前较短的时间内就得到,而且可以运用的历史数据不多,因此需要选用建模简单,收敛较快,所需数据量少又相对精度较高的方法。在很多的风电场风速预测中会采用神经网络进行建模[1-2],但是BP神经网络存在收敛速度慢,建模更复杂且容易陷入局部极小点等缺点,因此本文主要采用了时间序列预测和卡尔曼融合预测,在时间序列建模的过程中本文还进行了多次的模型检验使得建立的模型更精确,最终融合预测得到的数据的误差率也非常小,在预测速度,建模的难度和预测精确度上完全满足需求。
1 原理简介
1.1 风的预测
风的预测根据是否使用气象数据通常可以分为两类:一类是使用数值气象预报的预测方法;另一类是基于历史数据的预测方法[3]。按照预测周期长短则可以分为短期和长期预测:短期预测主要对每秒、分钟、小时的短期实测风速风向序列建立预测模型,来得到未来数分钟或数小时的预测值;而长期预测主要对日、月、年的长期实测序列建立预测模型,来获取未来较长时间的预测值[4]。
本文的预测是采用历史数据的短期预测,短期预测的方法有很多种,包括最小二乘法以及神经网络法、时间序列法、卡尔曼滤波法、遗传算法、小波分析及其他算法[5-11]。本文主要基于时间序列分析和卡尔曼滤波法。
1.2 时间序列分析
时间序列是指按照时间顺序记录的一组有序数据。对这组数据进行分析并得到它的规律从而预测它的未来走势的方法称为时间序列分析。时间序列分析的优点在于不必深究数据的来源和环境,数据本身携带的信息就足以建模,但是存在低阶的模型精度较低,高阶模型计算复杂的问题。
时间序列分析的主要流程如图1所示。
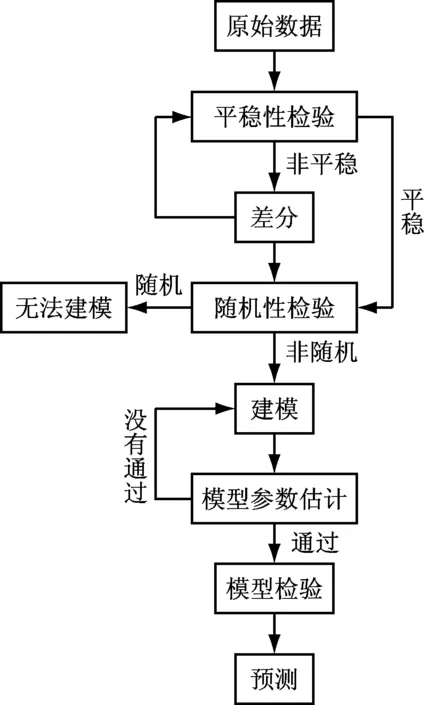
图1 时间序列分析流程图
其中平稳性检验主要方法有两种,一是根据时序图和自相关图的特征进行判断,二是构造检验统计量进行假设检验的方法例如单位根检验[12]。对于平稳时间序列建模的方法主要有三种:Box-Jenkins建模方法[13],Pandit-Wu建模方法[14]和长自回归、白噪化建模方法。时序模型主要包含平稳模型和非平稳模型。平稳模型主要有自回归(AR)模型,滑动平均(MA)模型和自回归滑动平均(ARMA)模型。非平稳模型有差分自回归滑动平均(ARIMA)模型等。
1.3 卡尔曼滤波
对于一个线性离散系统,可以用一个含随机项的差分方程和测量方程来描述为式(1)、(2)。
X(k)=AX(k-1)+BU(k)+W(k)
(1)
Z(k)=HX(k)+V(k)
(2)
式中:X(k)是k时刻的系统状态,U(k)是k时刻对系统的控制量。A和B是系统参数。Z(k)是k时刻的测量值,H是测量系统的参数。W(k)和V(k)分别表示过程和测量的噪声,它们的协方差分别是Q和R。
卡尔曼滤波主要包括两个过程:预估和校正。预估是利用时间更新方程对状态量和协方差进行估计;校正是利用状态更新方程进行反馈[15]。两组方程如式(3)、(4)。
时间更新方程:
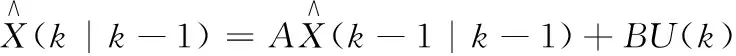
(3)
P(k|k-1)=AP(k-1|k-1)AT+Q
(4)
状态更新方程为式(5)—式(7)。
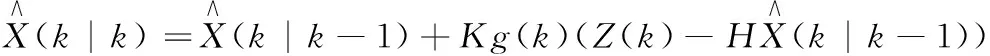
(5)
Kg(k)=P(k|k-1)HT/(HP(k|k-1)HT+R)
(6)
P(k|k)=(I-Kg(k)H)P(k|k-1)
(7)
式中:P表示对应状态的协方差,Kg为卡尔曼增益,I为单位矩阵。
卡尔曼滤波存在反馈机制,因此能够动态修改增益,预测精度相对较高,但是存在状态方程、测量方程和噪声方差较难建立的问题[16]。在本文中将卡尔曼滤波和时间序列分析法结合可以解决这个问题。
2 时间序列法预测风速风向
2.1 数据来源
为了监测整个场地海面环境,我们设计了一个海面监测系统,在场地的固定区域和教练艇上我们分别放置了多个风速仪和测流棒,本文的数据就来源于风速仪。通过简单的预测之后我们还可以在教练艇的手持终端上实时观看当前的海面风流情况,另外在PC端还设计了相应的数据库和数据分析软件来存储数据并且获取环境的特征和信息。
2.2 时序模型
时间序列分析法中对于非平稳序列通常运用ARIMA(p,d,q)模型进行拟合。具体表达式如式(8)—式(11)。
(8)
式中:
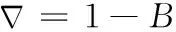
(9)
φ(B)=1-φ1B-φ2B2-…-φpBp
(10)
θ(B)=1-θ1B-θ2B-…-θqBq
(11)
其中at表示残差,是零均值白噪声序列;φi和θj是模型待估系数;B为后移差分算子。
2.3 实际预测
本文采用天津某帆船比赛场地2016年9月10日的内场的风速风向数据进行实例分析。数据的采样率是每秒一个点。采用的建模方法是Box-Jenkins建模方法。
首先选取风速数据的前400个点作为拟合点,记为序列{Xt},画出它的时序图,如图2所示。
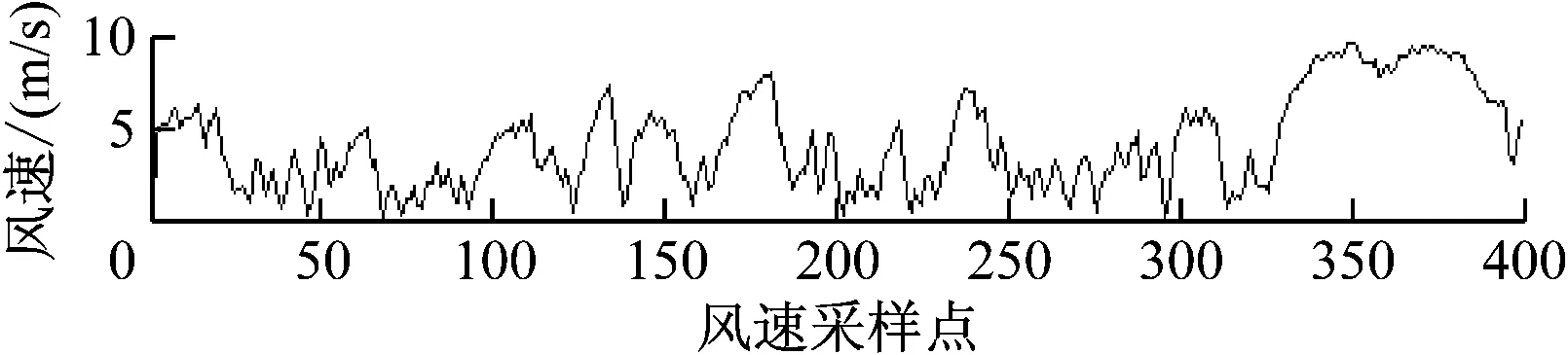
图2 {Xt}时序图
选取前20个点,画出它的自相关图和偏自相关图,如图3图4所示。
平稳序列的时序图应该具有在一个常值附近随机波动,并且波动范围有界的特点。另外平稳序列通常具有短期相关性,所以平稳序列的自相关系数和偏自相关系数不是截尾就是拖尾。截尾就是在某阶之后,系数都为0;拖尾就是有一个衰减的趋势,但是不都为0。根据图2、3、4就可以初步判断此序列是非平稳的。

图3 {Xt}自相关图
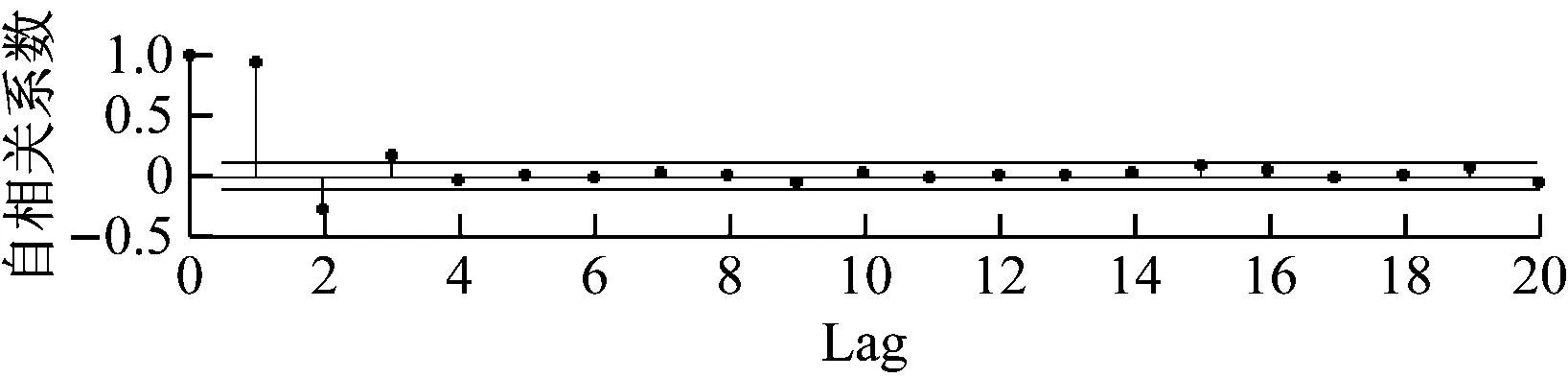
图4 {Xt}偏自相关图
对序列{Xt}进行一阶差分得到序列{Yt},该序列的时序图如图5所示。
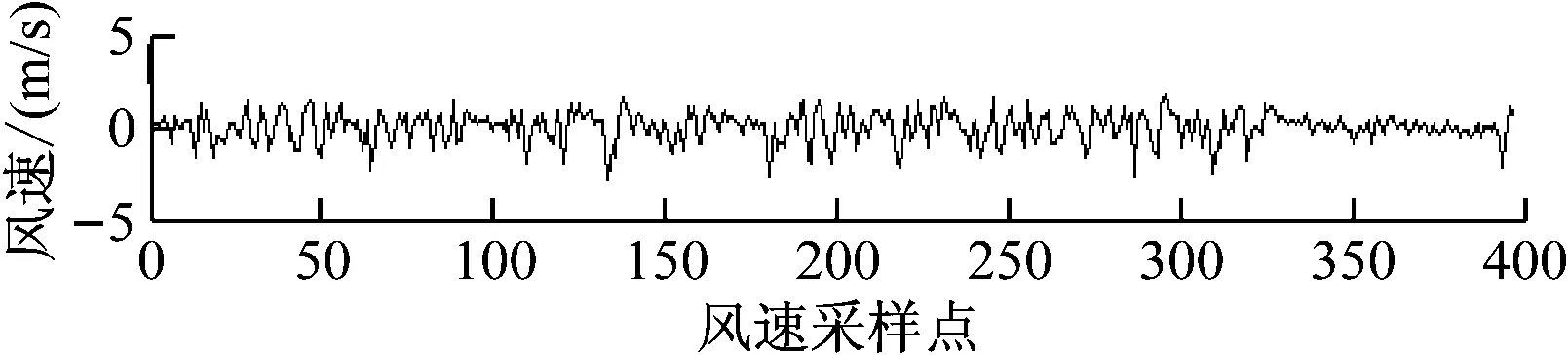
图5 {Yt}时序图
同样选取前20个点画出自相关图和偏自相关图如图6图7所示。图5显示序列{Yt}在某个常值附近波动,图6和图7显示该序列的自相关图和偏自相关图都呈现拖尾状态,序列{Yt}已经呈现平稳性,同时运用单位根检验可以加以确定。
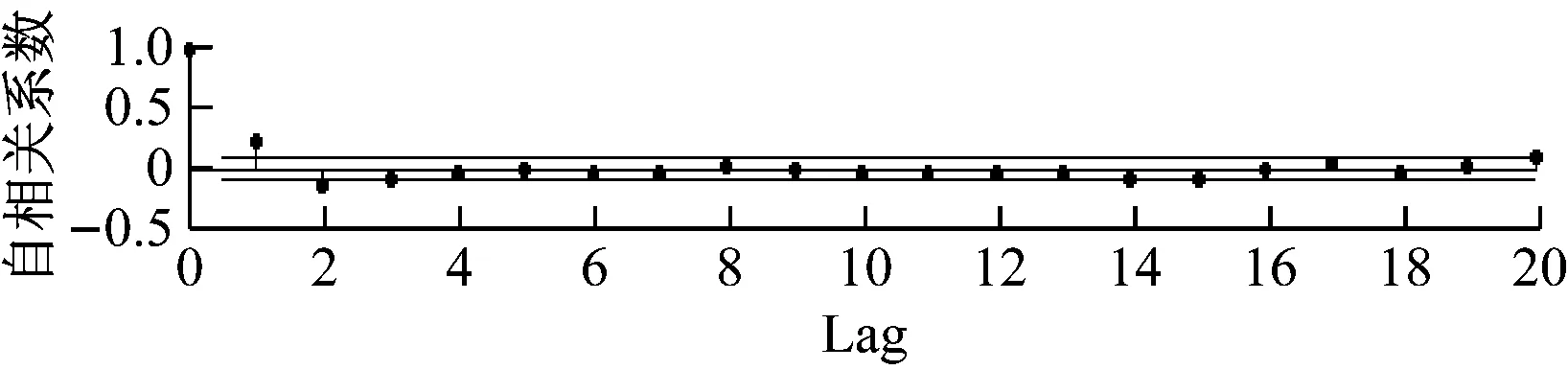
图6 {Yt}自相关图
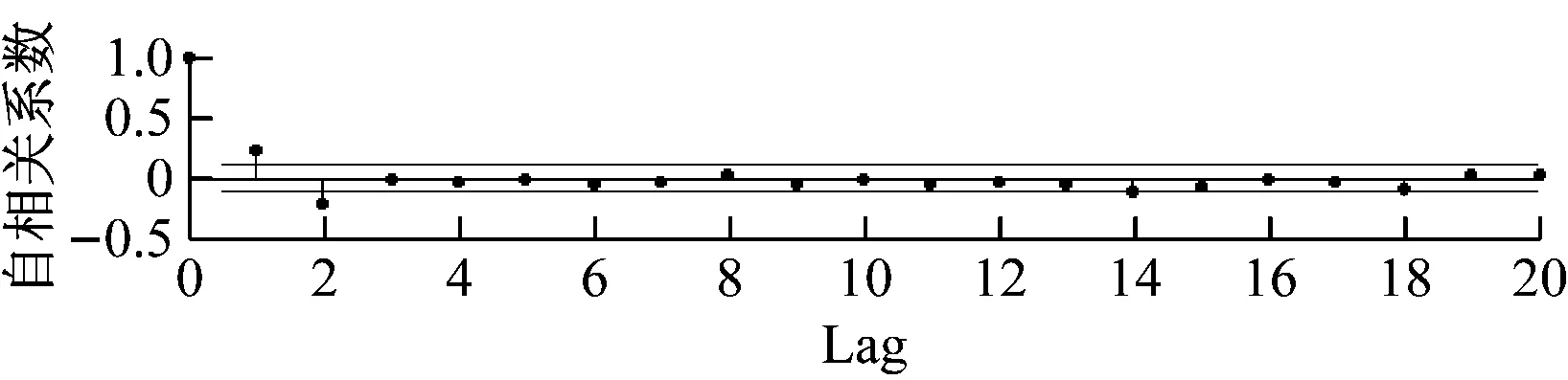
图7 {Yt}偏自相关图
通过随机性检验之后,利用AIC准则对序列{Yt}进行定阶建模,得到模型为AR(2)。最终由此得到序列{Xt}的模型为ARIMA(2,1,0)。通过最小二乘估计法计算得到该模型方程为式(12)~式(14)。
(1-0.296 9B+0.238 1B2)(1-B)X(t)=at
(12)
X(t)=1.296 9X(t-1)-0.535X(t-2)+0.238 1X(t-3)+a(t)
(13)
式中,a(t)表示模型残差。因此预测方程为:
X(t)=1.296 9X(t-1)-0.535X(t-2)+
0.238 1X(t-3)
(14)
最后为了确保模型的可用性和有效性还需要对模型残差进行检验。一个好的拟合模型应该能够提取观察值序列中几乎所有的样本相关信息,即残差序列中不包含任何有用信息。对残差的检验结果,如图8所示。
可以看出残差符合白噪声序列的特征,表明该模型有效。那么利用预测方程式(14),设定预测步长为1(即预测一个点之后就需代入一个实际数据再进行下一个点的预测),预测后100个点的风速数据,可以得到风速的超前一步预测曲线和实际风速曲线的对比图如图9所示。
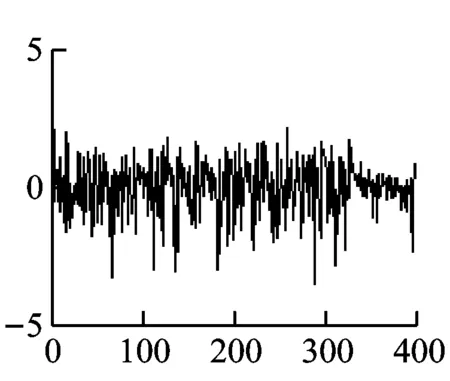
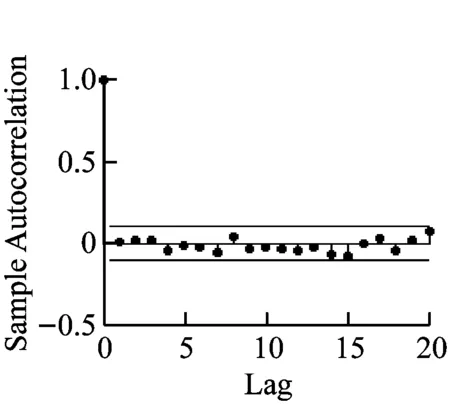
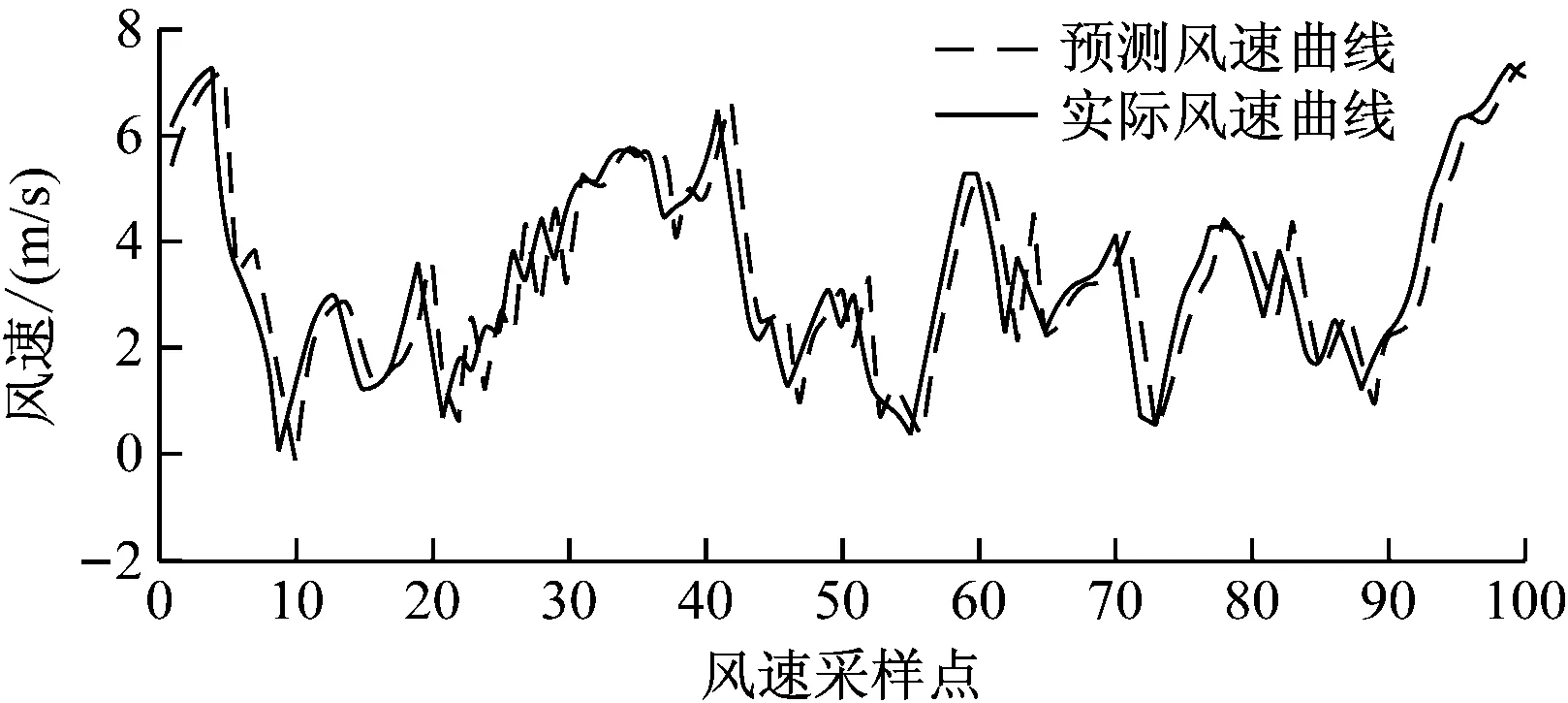
图9 时间序列超前一步风速预测结果图
从图9可以看出上述的预测方法和模型是可行的。同样改变预测步长可以得到超前多步的风速预测曲线如图10、11所示。
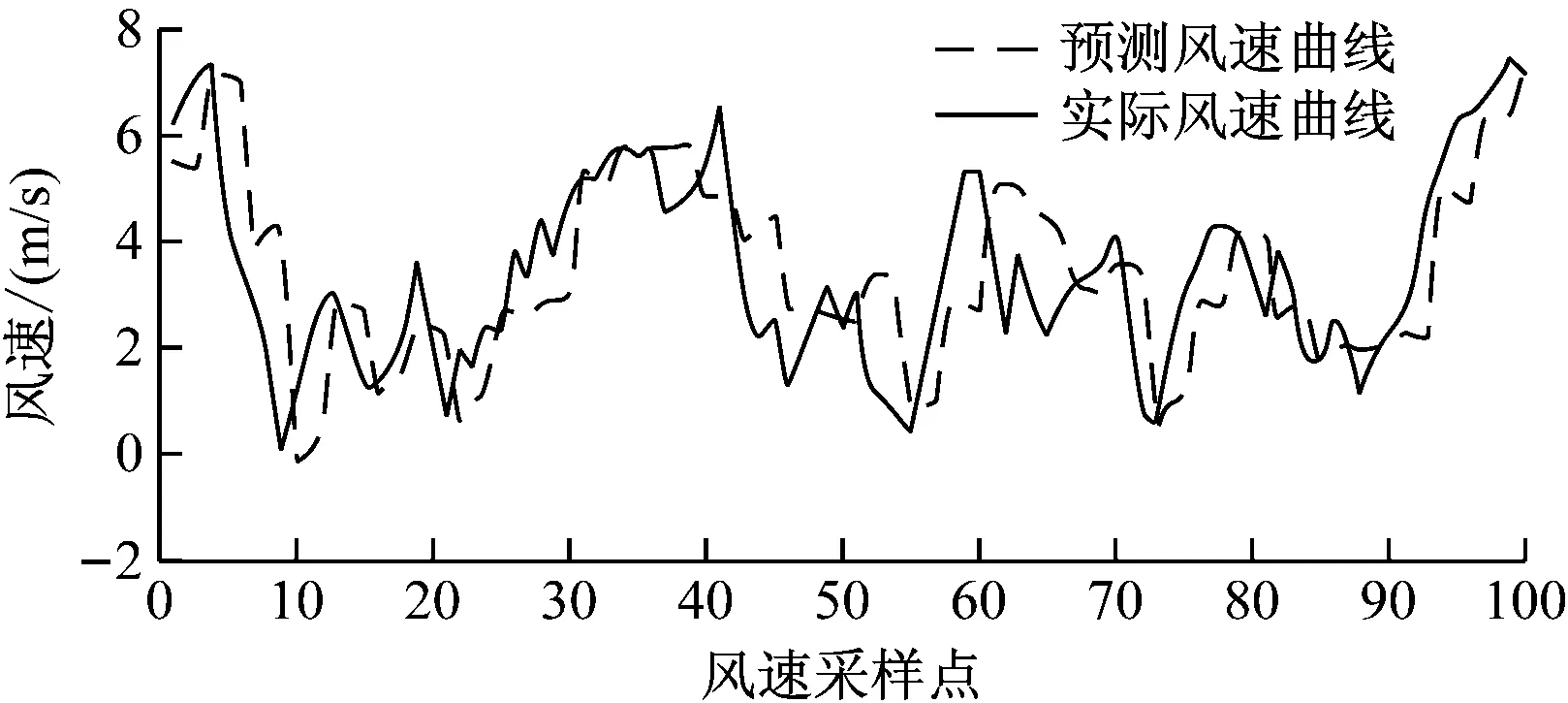
图10 时间序列超前3步风速预测结果图
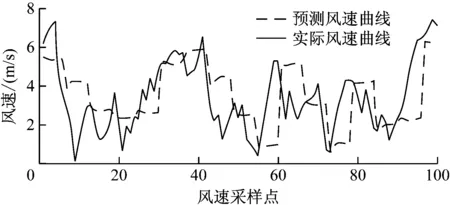
图11 时间序列超前6步风速预测结果图
从图9—11可以看出用时间序列分析法进行预测的结果基本符合风速的变化趋势但是存在明显的延时性,且预测步长越大预测的曲线与实际曲线的吻合度越低。通常风速预测结果的相对平均误差变化范围是25%到40%[17-18],运用以下误差计算如式(15)~式(19)。
(15)
(16)
(17)
(18)
(19)
式中,Xi表示第i个实际风速值,Fi表示第i个预测风速值。其中平均误差(ME),平均绝对误差(MAD)和均方误差(MSE)的大小受时间序列数据的水平和计量单位的影响,因此不能真正反映预测模型的好坏,只有在比较不同模型对同一数据的预测时才有用,而平均百分比误差(MPE)和平均绝对百分比误差(MAPE)反映了误差的相对值。通过计算最终可以得到误差分析结果,如表1所示。
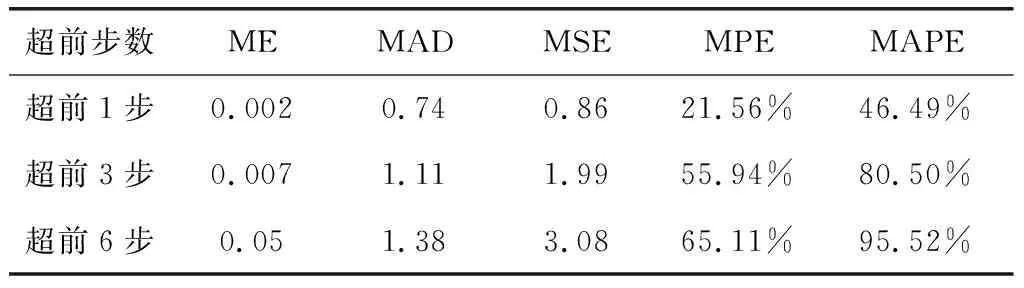
表1 时间序列风速预测误差表
从表1中的数据可以看出时间序列预测的精度不高且超前步长越大误差越大。其中数据跳变处的误差是最大的。
用同样的方法可以对风向进行预测,最后得到的预测模型为ARMA(1,4),预测方程和超前一步预测曲线如下式中R(i)表示第i个实际值。超前一步预测的MPE为23.72%,MAPE为54.82%,如式(20)。
X(i)=X(i-1)+0.8*(R(i-1)-X(i-1))+
0.090 9*(R(i-2)-X(i-1))-
0.108 1*(R(i-3)-X(i-3))+
0.128 2*(R(i-4)-X(i-4))
(20)

图12 时间序列超前一步风向预测结果图
3 卡尔曼融合预测
3.1 卡尔曼预测
卡尔曼预测的精度较高,但是状态方程和测量方程比较难建立,因此在这里与时间序列预测法相结合。先通过时间序列分析得到一个模型,然后根据模型直接推导出卡尔曼滤波的状态和测量方程,最后利用卡尔曼预测迭代方程进行预测。
3.2 卡尔曼融合预测
根据时间序列预测已经得到风速的模型方程为式(13),因为此方中存在3个时间延迟,因此需要将式子转化为矩阵形式。首先将式(13)改写成如下式(21)。
X(k+1)=1.296 9X(k)-0.535X(k-1)+
0.238 1X(k-2)+a(k+1)
(21)
假设X1(k)=X(k),X2(k)=X(k-1),X3(k)=X(k-2),就可以得到式(22)。
X1(k+1)=1.296 9X1(k)-0.535X2(k)+
0.238 1X3(k)+ak+1
(22)
因为X2(k+1)=X1(k),X3(k+1)=X2(k),由此可以得到状态方程和测量方程如式(23)、(24)。
(23)
(24)
式中,w(k)表示过程噪声,v(k)表示测量噪声,一般它们的协方差比较难确定,测量协方差R可以根据测量值进行离线确定,过程协方差由于前面已经用时间序列做了预测,因此在这里将时间序列预测的过程噪声协方差作为Q的取值。将式(23)、(24)与式(1)、(2)进行对照可以得到参数A、B、H的值。另外在这里取X(0|0)=0,P(0|0)=10I,因为最终算法会收敛,初始值不会有影响。最后利用MATLAB进行混合算法的编程预测可以得到预测曲线,如图13所示。
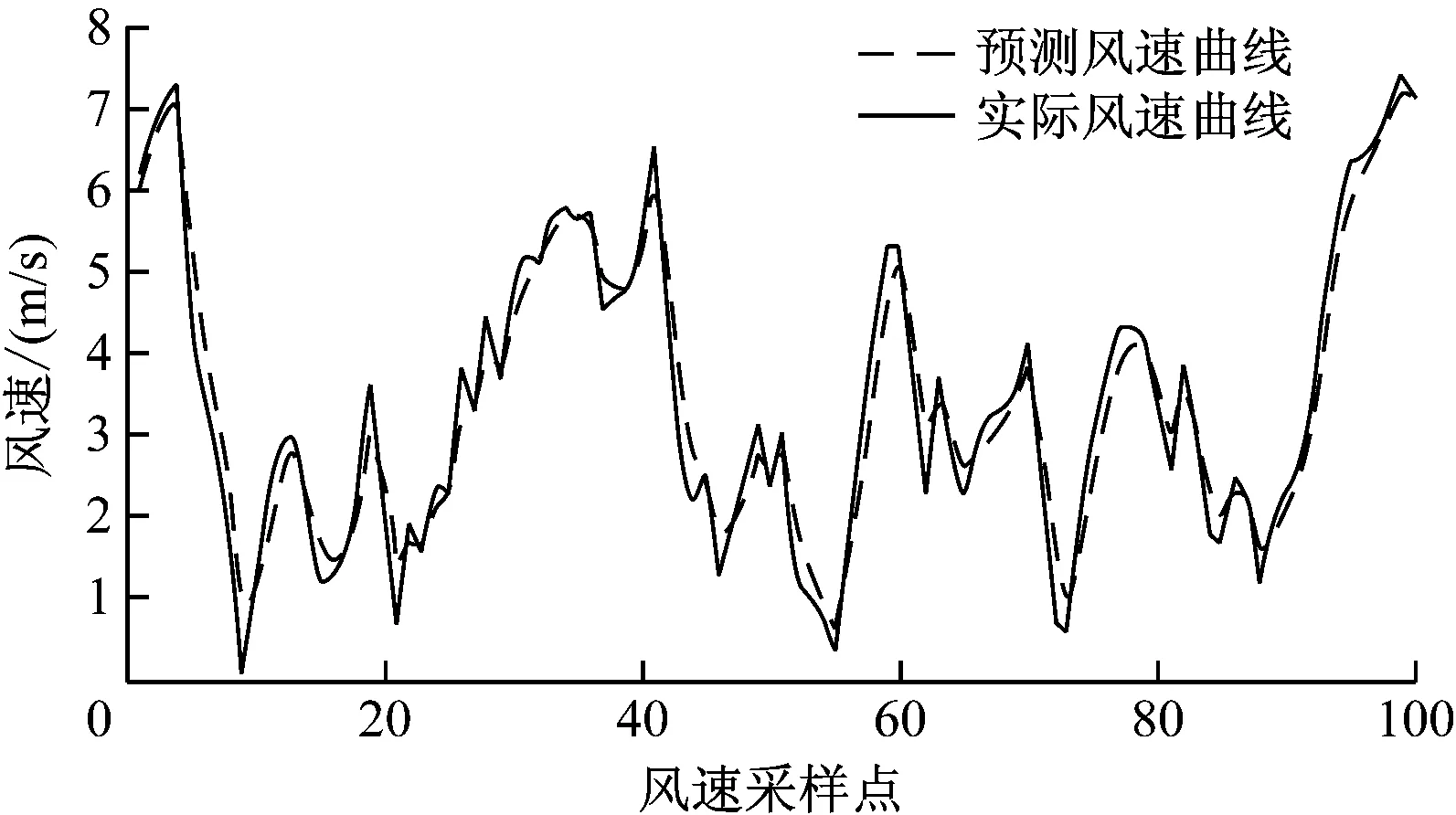
图13 卡尔曼融合风速预测结果图
运用同样的方法可以对风向的预测也采用融合方法,最后得到的预测图形和原始图形如图14所示。
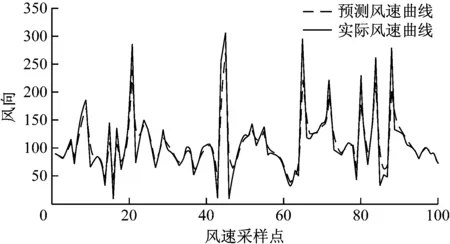
图14 卡尔曼融合风向预测结果图
从图13、14中可以看出卡尔曼融合算法解决了时间序列预测的时延问题,表2的数据也显示了融合算法对预测精度有很明显的提升,融合算法对于风速的预测平均百分比误差(MPE)只有2.14%,平均绝对百分比误差(MAPE)为13.58%;对于风向的预测MPE为4.07%,MAPE为14.55%。虽然卡尔曼融合算法提高了预测精度,但是还是可以从图13、14中看出该算法在数据跳变处的预测不是很精确。

表2 时间序列预测和卡尔曼融合预测误差表
3.3 数据分析
对于风速风向的预测最终是要为运动员的帆船训练和比赛服务,然而直接预测得到的风速风向数据对于帆船运动来说并没有特别大的实际意义,我们还需要对这些预测数据进行特定的数据分析,最后得出的结论对运动员和教练来说更直观,才具有较大的实际意义。因此在PC端我们利用MATLAB设计了一个海面风速风向数据分析软件,具体的算法和实现效果如下:
具体的数据分析主要分为两类,一类是基本数据特征的提取,另一类是数据的统计分析。
对于第一类的数据分析我们采用表格形式显示,比如平均值、最大最小值、标准差等等。
第二类的数据分析通过饼图的形式进行表现,主要有两种类型的分析。第一种是对同一位置的风速风向进行分析,可以得到这个位置的风速风向的特性,第二种是对两个不同位置的风速风向进行分析,可以从中得到整个环境的风速风向的特征。
第一种对于同一位置的数据分析可以分为三块。第一块是对于同一位置的一段时间内的风向数据进行风摆时间分析。简单来讲就是在研究的时间段内将每一时刻的风向和这段时间内这个位置的矢量平均风向逐一进行比较。大于矢量平均的就是风向右偏,我们将它定义为右摆,用R表示,反之则是左摆,用L表示。当然这里还定义了一个风向比较的阈值,只有瞬时风向和矢量平均风向的差值大于这个阈值时才能比较它们的大小,否则将这两个值视为相等,用“=”表示,即两个角度几乎没有差别。具体的计算分析过程如下:
(1) 先计算截取时间段内该位置的平均风向值(矢量平均)
(2) 然后统计出
每秒风向值>平均风向值的概率——右摆概率(R)
每秒风向值<平均风向值的概率——左摆概率(L)
每秒风向值=平均风向值的概率——近似相等概率(=)
(*存在阈值判断,例如风向值偏离3度,有风摆。)
第二块是对于同一位置的一段时间内的风速进行风速上下分布分析。基本分析方法就是在研究的时间段内将每一时刻的风速和这段时间内这个位置的矢量平均风速进行逐一进行比较。大于矢量平均风速的将它定义为强风,用G表示,反之则为无风(也可定义为弱风),用La表示。在分析中同样定义一个风速比较的阈值,只有瞬时风速和矢量平均风速的差值大于这个阈值时才能进行大小的比较,否则将这两个值视为相等,即无明显差异,用“=”表示。其中需要注意的是这里所有风速的单位都为节(knot),单位符号kn或kt,是一个专用于航海的速率单位,后来延伸至航空领域,相当于船只或者飞机每小时所航行的海里数,和标准速度单位m/s的转换是1节约等于0.514 m/s。具体的分析计算过程如下:
(1) 先计算截取时间段内该位置的平均风速值(矢量平均)
(2) 然后统计出
每秒风速值>平均风速值的概率——强风概率G)
每秒风速值<平均风速值的概率——无风概率(La)
每秒风速值=平均风速值的概率——近似相等概率(=)
(*存在阈值判断,例如风速值偏离1节,有阵风。)
第三块是对于前面两种分析的结合,最后可以得到阵风来源分布图或者称为风摆规律图。其实就是将风速风向数据分成右偏强风、右偏无风、左偏强风和左偏无风四类,分别用RG、Rla、LG、Lla表示,这里将近似相等的数据忽略因为分析的意义不大。
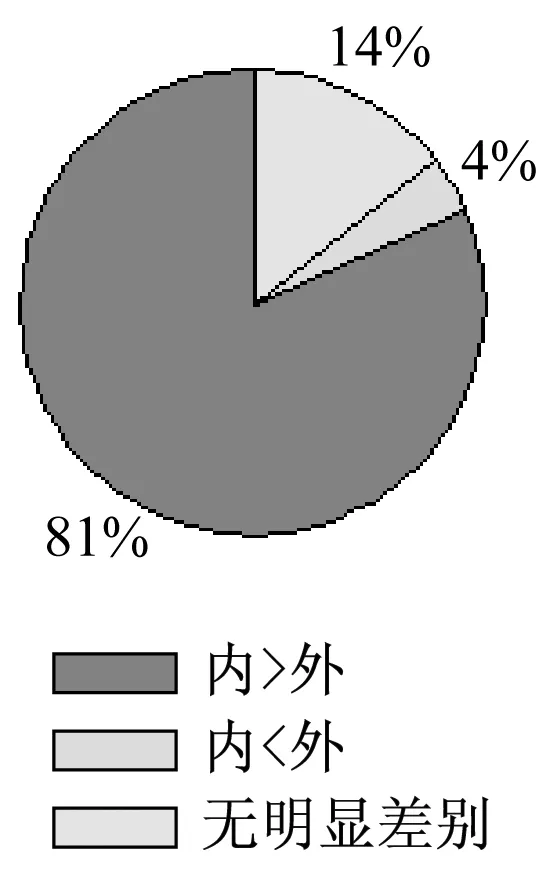
第二种对于不同位置的数据分析也分为两小块。第一块是对于不同位置的风速进行比较。将不同位置相同时间段的风速进行逐一比较,最后得到三种情况的概率,分别是A位置风速大于B位置风速、A位置风速小于B位置风速、A位置风速等于B位置风速,同样也设置了阈值,相差小于阈值的就判定为两个位置风速相等。具体的分析计算流程如下:
(1) 先计算每5分钟内的平均风速值
(2) 然后统计出
A位置风速值>B位置风速值的概率
A位置风速值 A位置风速值=B位置风速值的概率 (*存在阈值,例如风速值大于1节,为有差异。) 第二块是对于不同位置的风向比较,对于大跨度时间的数据来说风向的比较没有很大的意义,因为很难分析出比较重要的信息,但是对于截取的一段时间的风向数据来讲,通过分析可以大致判断风向是左偏还是右偏,对于运动员训练和比赛是有很大的作用的。分析的方法和前面第一块风速分析的类似,具体如下: (1) 先计算每5分钟内的平均风向值 (2) 然后统计出 A位置风向值>B位置风向值的概率 A位置风向值 A位置风向值=B位置风向值的概率 (*存在阈值,例如风向值大于5度,为有差异。) 利用以上算法我们可以对融合预测出来的数据进行简单的数据分析,因为涉及到不同位置的数据比较,在此先运用卡尔曼融合预测算法得到天津该帆船比赛场地2016年9月10日的内场和外场下午1点到2点的风速风向预测数据。最后经过分析得到的结果如图15、16所示。 从上面的图表中可以得到内场在该时间段内风速风向的变化较大,没有明显的趋势,另外内场的风速比外场大,风向相较于正北方向更偏东。这些结论对运动员的比赛就有很大帮助。 帆船运动是一项主要依靠自然风力作用于风帆,同时借助运动员操控风帆和调整船体姿态驾驶船只行驶的水上运动[19]。此运动的比赛环境比较复杂,海面的风速风向,海流的流速流向等都有较大的影响。因此,如果对比赛环境的一些特定参数进行相应的分析量化和预测就会对帆船训练以及比赛提供很大的帮助。 本文采用时间序列预测和卡尔曼融合预测两种方法对海面风速风向进行了短期预测,实验证明时间序列预测建模简单,可以有效地对风速风向进行短期预测但是存在时延和预测精度不高的问题,在进行多步预测后发现步长越大预测精度越低;采用卡尔曼融合预测可以有效提高预测精度,但是在数据跳变处误差仍然较大。为了解决这个问题可以在后续实验中先对数据进行预处理比如滤波等然后再进行预测。 本文最后对预测的数据进行特定的数据分析,得出的图表可以直观的显示比赛环境的风速风向特征,为运动的训练和比赛提供指导意义。 最终两种预测算法和数据分析已经可以实际应用,在巴西奥运会和天津全运会中为帆船比赛提供了帮助。 在风速风向短期预测中还存在其他不同的算法,采用更好的方法预测的精度也会更高,后续将研究其他的算法以及多种算法的融合提高预测的精度,使得预测结果在帆船运动中有更好的应用;另外将继续深入研究分析算法,利用风速风向数据得出更有意义的结果,为我国帆船运动提供助力。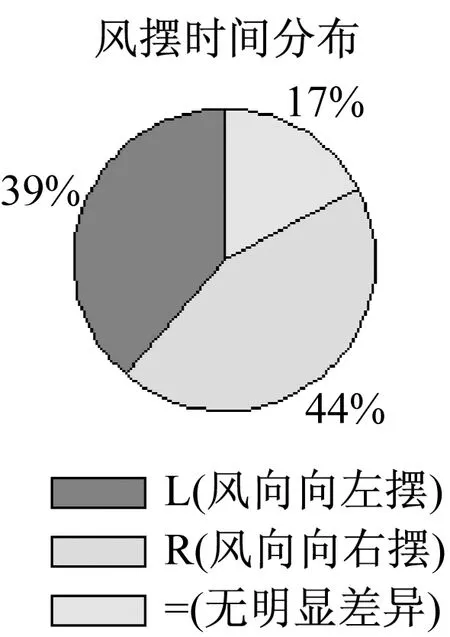
4 总结
