YXG500连续墙抓斗瞬态响应分析及寿命评估

刘本学，王庆会，程伟威

（1. 郑州大学 机械工程学院，河南 郑州 450001；2. 宇通客车股份有限公司，河南 郑州 450016）

连续墙成槽机由工程车体和连续墙抓斗两部分组成，本文针对连续墙抓斗展开分析。虽在近几十年对连续墙机构已经进行了大量的探测和研究，但由于抓斗斗体结构较为复杂，故在运用CAE进行加载分析时对实际的操作要求较高，导致以往的研究往往会忽略掉一些负载来使分析过程得以简化，这样可能会使得抓斗斗体的分析偏差较大。本文在以往研究的基础上对抓斗的实际工作环境作出了深度细致的分析，并通过ANSYS软件对连续墙抓斗在不同工况下进行了数值模拟，并对其寿命进行了评估，为工业上连续墙抓斗的生产设计及工程应用中的可靠性提供了参考。

1 工作载荷的确定及瞬态响应理论

1.1 YXG500连续墙抓斗的工况分析

（1）抓斗施放工况。主要的载荷为配重G1、主转台自重G2和臂架支反力F1，撑杆支反力F2和变幅钢丝绳拉力F3，如图1所示。该工况主要是在配重作用下，主转台受弯。

（2）克服吸附力工况。在抓斗开始提升时会有吸附力存在，吸附力约为抓斗自重和土重之和的0.5倍，因此该工况也必须予以考虑。吸附力工况的受力如图2所示，除配重和自重外，其他力增加较多。

图1 抓斗施放工况

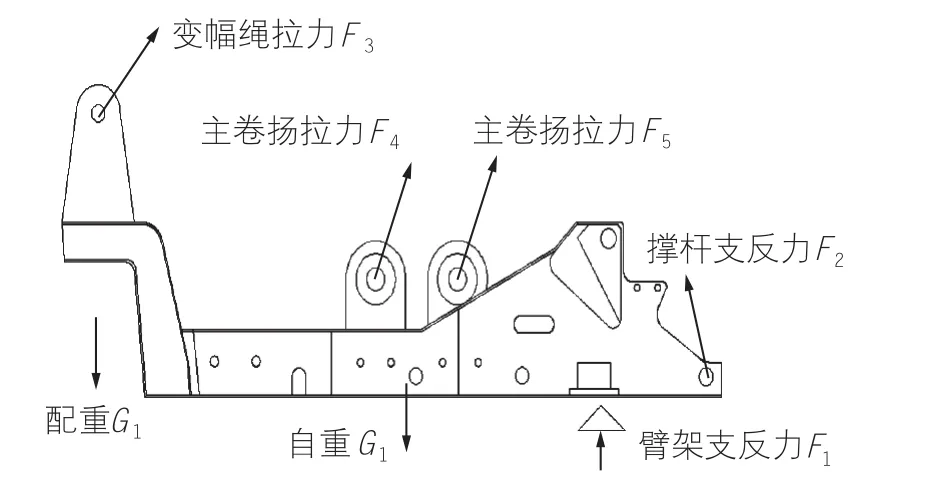
图2 克服吸附力工况

（3）抓斗抓土提升工况（最大抓土量为1t）。抓斗抓土提升工况受力形式与图2相同，除配重和自重外，其他力都有所减小，主卷扬拉力F4、F5均变为102900N。

（4）抓斗吊起工况。抓斗吊起工况受力形式与图2相同，除配重和自重外，其他力都有所减小，主卷扬拉力F4、F5均变为98000N。

连续墙抓斗工作过程中，臂头受到的拉力变化如图3所示。工况1为克服吸附力工况，工况2为抓斗抓土提升工况，工况3为抓斗吊起工况，工况4为抓斗施放工况。由图3可以看出，工况3臂头受到的应力变化较小，故此时整机受到的损伤较小，可以忽略，因此瞬态计算中只考虑工况1、工况2和工况4。

图3 臂头受力与时间的关系

1.2 瞬态响应分析的基本理论

（1）瞬态响应的过程。

对固定时间段Δt求出离散点的响应，用中心差分法

其中，[A1]=[M/Δt-+B/2Δt+K/3]为动态矩阵，[A2]=1/3{Pn+1+Pn+Pn-1}为作用力，[A3]=[2M/Δt2-K/3]和[A4]=[-M/Δt2+B/2Δt-K/3]为初始条件。

（2）瞬态响应分析中的阻尼。

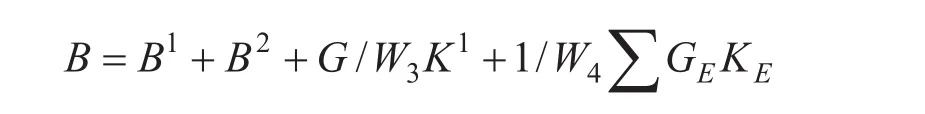
其中，B1=阻尼单元+B2GG，B2=B2PP直接输入矩阵+传递函数，G为整体结构阻尼系数，W3为感兴趣的整体结构阻尼转化为频率-弧度/秒，K1为整体刚度矩阵，GE为单元结构阻尼系数，W4为感兴趣的单元结构阻尼转化为频率-弧度/秒，KE为单元刚度矩阵。

2 模型建立及分析步的确定

2.1 模型建立

为了得到主转台的真实受力，建立了包括臂架、撑杆、主转台等整体模型，并进行了网格划分。在此基础上对部分非完整焊接结构进行了修改，并对尾部模型网格加粗，如图4所示。对实际破坏部位进行了网格加密，如图5所示。

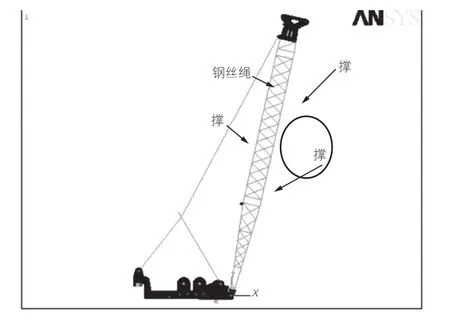
图4 整体网格模型

图5 网格加密区

2.2 分析步的确定

分析步Δt可以根据对结构响应有主要贡献的若干固有振型的周期来确定。先对整机做模态分析：对转盘处进行全约束，结果如表1所示。整机的1阶固有频率为f=2.2174，最小时间步长Δt=1/20f=0.0225s，计算中实际选择的时间步长为Δt=0.02s。

表1 整机模态分析

3 材料参数

为进一步得到所用材料的抗拉强度，通过理化室化验后得到了相关参数。考虑到安全性取下限，即应力计算时输入材料的抗拉极限为525MPa，相关材料信息如表2和表3所示。

表2 构件材料名称

4 计算结果及分析

由图6和图7可以看出，由于臂头突然受到31.5T的拉力，使整机产生了一个自由振动的过程，危险位置第一主应力最大应力幅值约为80MPa；由图8和图9可以看出，由于臂头处吊重由31.5t减少到21t，使整机产生了一个自由振动过程，危险位置第一主应力最大应力幅值约为50MPa。

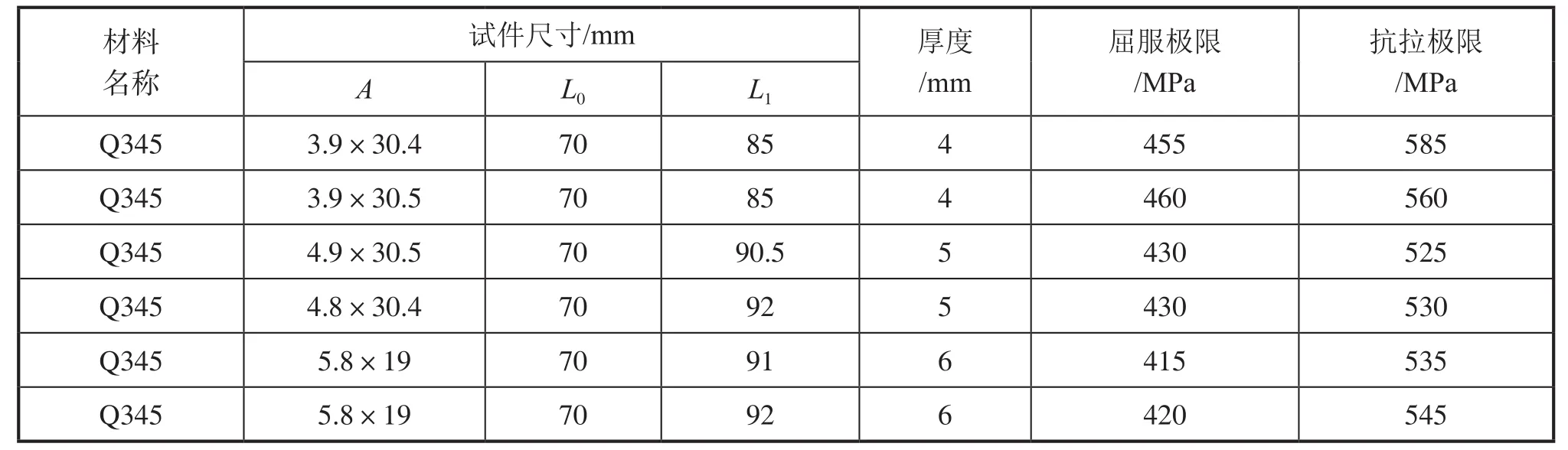
表3 Q345拉伸试验数据

图6 工况1臂头处X方向位移时间历程

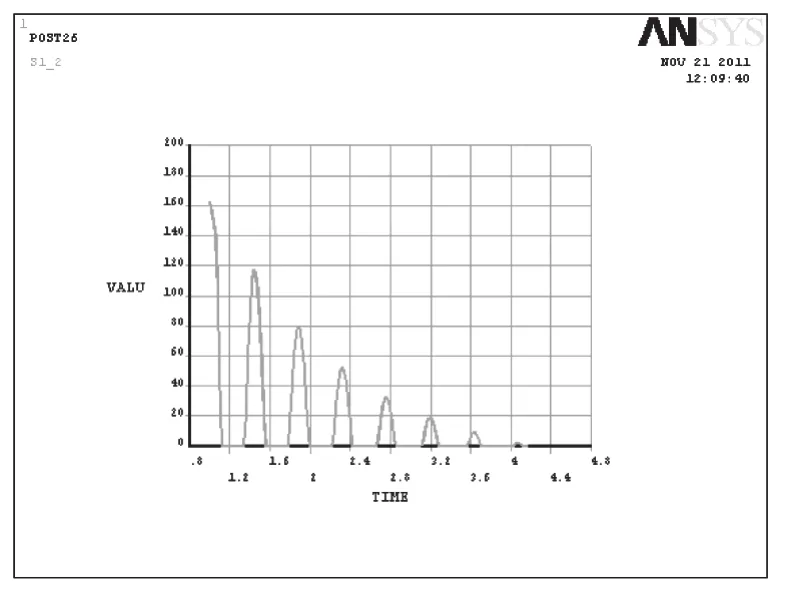
图7 工况1危险位置第一主应力的时间历程

由图10和图11可以看出，主转台在配重和臂架的作用下，以转盘为支点上下振动。当臂架前倾时，转台受到向上的拉力。可见释放吊重后，转台的振动由两部分组成：在配重作用下的自由振动（此时臂架后仰）和强迫振动（当臂架前倾时）。

图8 工况2臂头处X方向位移时间历程

图9 工况2危险位置第一主应力的时间历程

图10 工况4臂头处X方向位移时间历程

图11 工况4危险位置第一主应力的时间历程

5 疲劳寿命理论及疲劳分析

5.1 疲劳寿命理论

（1）Sbe的确定。

本次分析时材料的抗拉极限采用了估算的方法，抗拉极限的数值为525MPa。当R=-1时，旋转弯曲载荷作用下的疲劳极限估算公式为

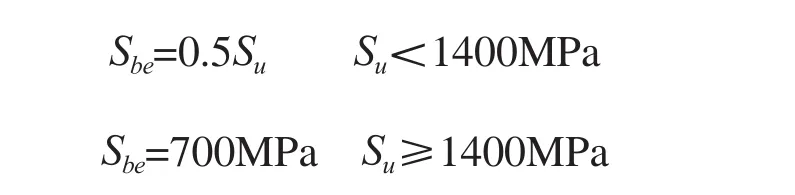
本次分析时，Su=525MPa，代入可得Sbe=262.5MPa。

（2）S1000的确定。

103次循环时的疲劳强度取决于可靠性水平和加载类型。

CR为在规定可靠性水平下的修正系数，本次可靠性取0.5，查表得到CR=1。对于全弯曲工况下，S1000=0.9Su=472.5MPa。带入可得S1000，R=472.5MPa。

（3）构件的疲劳极限。

代入数据可得Se=146.42MPa。

构件S-N曲线是通过材料S-N曲线修正得到，如图12所示，在对数坐标系中，求得坐标点A（103，472.5）和点B（106，146.42），代入

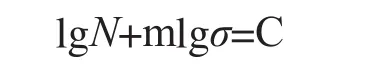
式中，m和C为常数，N为循环次数，σ为应力幅值，可求得直线的方程为

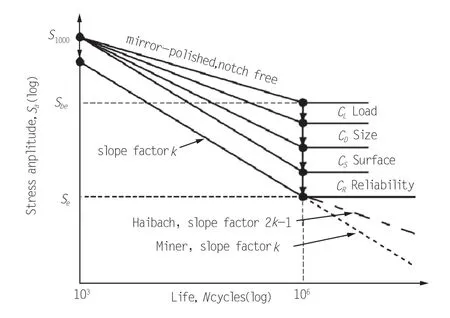
图12 构件的S-N曲线

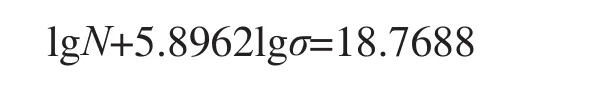
将A、B点坐标导入LMS.Durability中得到结构的S-N曲线，如图13所示。

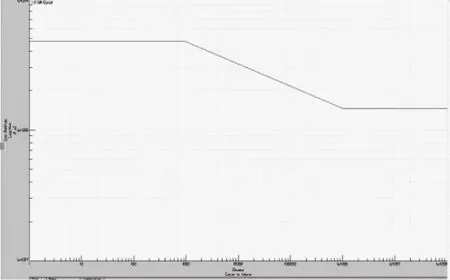
图13 结构S-N曲线

5.2 计算结果及分析

由图14可知最大损伤值为2.24e-5，即44642次，由图15可以看出热点出现的位置与实际破坏的位置相同。按照1天工作500次循环，则寿命为3个月。而此抓斗在实际工作中，使用2个月左右时间后在热点位置发生焊缝开裂，两者误差约为33%。

图14 疲劳损伤云图

图15 热点位置

6 结束语

本文通过对实际工程中连续墙抓斗的实际破坏位置进行受力分析，得出以下结论：

（1）连续墙抓斗的危险位置在克服吸附力工况下受到的第一主应力幅值约为80MPa；在抓斗提升工况下受到的第一主应力幅值约为50MPa；在抓斗施放工况下抓斗的振动由自由振动和强迫振动两部分组成。

（2）3个工况下应力幅值变化最大处都发生在网格加密区域（即危险区域，见图5），故该处便为应力的集中区域。

（3）该连续墙抓斗的理论寿命为2.24e-5，即连续墙抓斗的热点位置在循环44642次左右时将会发生破坏。按照1天循环500次，则寿命为3个月左右。

由此可知，现阶段的连续墙抓斗可靠寿命较短，可从斗体和机械结构上对其进行优化，从而来提高连续墙抓斗的寿命。