基于能量方法的江浙地区抬梁式及穿斗式传统民居木构件重要性分析
2018-11-22孟哲,淳庆
孟 哲,淳 庆
(东南大学建筑学院,江苏南京 210096)
0 引 言
遗产建筑被称为“历史的见证”、“实物的历史”,具有唯一性和不可复制性,关键构件失效很有可能会导致整体结构的崩溃,造成巨大损失。近些年来,随着建筑遗产预防性保护理论和技术的发展,开展了许多古建筑的健康监测课题研究,而其中一个关键的技术问题是如何科学有效地确定建筑遗产监测的关键构件,因此构件重要性评估是预防性保护研究的一个重要环节。此外,对建筑遗产的构件重要性研究能够给修缮、施工以及维护提供科学合理的依据,针对关键构件采取加强的修缮措施以防止可能发生的大范围倒塌破坏。本工作以传统木构建筑为研究对象,选择抬梁式和穿斗式两种典型结构类型,对构件重要性研究进行探索。
构件的重要性通过构件功能对结构整体性能的贡献及影响来进行评价,它取决于结构的力学性能、荷载工况和评价指标。柳承茂等[1,2]将构件失效后对整体结构的影响面积作为评价指标。张雷鸣等[3]深入研究了结构系统的拓扑关系以及刚度分布,得到了重要性层次的计算方法。以上早期的研究所得的结果均与荷载作用无关,而构件重要度除了受几何和刚度分布等特性的影响,荷载工况也是重要的影响因素。已有许多学者在考虑荷载的情况下提出计算和评价方法,评价所研究的一般是静力系统,在确定的结构、确定的荷载作用下研究构件的重要度。NAFDAY[4]将完好结构与拆除构件后结构的刚度矩阵行列式的比值作为评价指标。JAHAN等[5]提出了平均应力比评价指标、刚度退化系数评价指标以及稳定退化系数评价指标。STEW等[6]基于重要性评价原理,开发相应的计算程序使功能得以实现。张松[7]和朱丽华[8]将改进的统计矩点估计法应用于构件重要性分析。叶列平等[9]以拆除构件对广义结构刚度的影响程度作为构件重要性评价指标,其中结构的广义刚度概念也可转化为更为直观的应变能进行替代。ZHU L H[10]等提出了综合考虑多因素的客观赋权法,并提出了评价指标和赋权系数。YANG Z等[11]、卢啸等[12]和骆城等[13]基于结构广义刚度评价方法,对实际的工程进行了重要性评估并证明了该方法的可行性。本研究借鉴基于广义刚度的评价方法,运用考虑荷载工况的基于能量的评价方法对木构建筑的重要性计算进行初步探索。
综上,目前对于构件重要性的研究主要集中在制定评价指标和结合工程应用,并且鲜有涉及传统木构建筑。在设计计算模型时参考了淳庆等[14,15]对传统木构受力性能的研究,选择江浙地区传统民居建筑的抬梁式和穿斗式两种典型的木构形式进行分析,依托有限元计算软件中的生死单元功能实现传统木构构件的重要性计算。许多学者的研究证明了该方法的可行性:HOSEYNI等[16]将生死单元法应用于机械接头的性能评估中;JIANG等[17]将该法应用于建筑结构施工力学分析。WANG等[18]运用该方法评估了某二战时期桥梁的构件重要性。本研究运用有限元软件Ansys开发了传统木构建筑的构件重要性计算程序,计算得到各个构件在竖向荷载、水平荷载作用下的构件重要性,并对它们进行排序,得到两种传统木构结构形式的关键构件。
1 基于能量方法的构件重要性评价
1.1 结构总应变能的概念与评价指标
应变能即以应变和应力的形式贮存在物体中的势能。对于一个保守的杆件结构系统,外荷载所作的功能够完全贮存在结构中,从而转化为该结构系统的应变能,总应变能即系统中所有杆件应变能之和。文献[9]中提出了以构件损失所导致的结构广义刚度(结构应变能)损失率作为衡量构件在结构中的重要程度指标,其简化后的表达式如式(1):
(1)
式中,K0和Kf分别为原始结构和某构件属性改变后的结构广义刚度;U0和Uf分别为原始结构和某构件属性改变后的结构总应变能。
该评价指标是针对杆系结构建立的,忽略了构件体积对重要性的影响。由于本研究运用有限元软件建立梁单元模型,为排除单元体积差异对结果的影响,参考文献[12]得到考虑单元体积影响的评价指标,其表达式见式(2):
(2)
式中,Ve为属性改变的单元的体积。
1.2 基于能量方法的构件重要性计算方法
基于能量方法的构件重要性计算多通过Ansys等有限元软件的生死单元功能实现。其原理是在单元被“杀死”时刚度接近于0,同时与该单元有关的载荷向量的输出值以及应力和应变均被重置为零,因而被“杀死”的单元不再对载荷生效。这种模拟方式可以近似等效于单元被删除的脆性失效,已被广泛地应用于混凝土框架和砌体结构的构件重要性评价中,而这种脆性失效情况有别于本研究所着眼的传统木构的结构损伤情况。
对于木结构古建筑损伤可大体分为:材料性能下降、构件开裂、挠度过大和榫卯节点损伤。由于木材是各向异性的非匀质材料,损伤多是塑性的,有别于生死单元法的模拟失效状态。针对木材的力学特性,本研究将生死单元法进行改进,提出了基于改变弹性模量的构件重要性计算方法。该方法为逐一降低单元的弹性模量(改为初始值的0.05%),得到它们对整体结构变形能的单位体积影响程度,再利用上文的评价指标进行评价排序。弹性模量改变的单元不同于被“杀死”的单元,它能够传递力并产生变形,更贴近真实状态下的木构损伤情况。
本研究运用能量方法,首先,对采用生死单元法和改变弹性模量法对传统木构的重要性评价进行了比较分析,对比得到更适用于传统木构建筑的构件重要性计算方法;其次,对传统木构单榀框架采用改变弹性模量法对结构在竖向荷载和水平地震作用下的构件重要性进行分析;最后,对一传统木构整体框架采用改变弹性模量法对结构在竖向荷载和水平地震作用下的构件重要性进行分析。
2 重要性评价计算模型的建立
2.1 木构架的几何参数
研究选择江浙地区最为常见的两种典型的传统木构形式进行分析,即抬梁式和穿斗式。江浙地区现存众多明清时期的民居木构建筑,无论在榫卯构造还是建筑形制方面,均明显不同于北方官式木构建筑。江浙地区抬梁式木构架的特点为:在柱顶沿进深方向架数层叠架的梁,梁逐层缩短,层间垫瓜柱,最上层梁中间立脊瓜柱形成三角形屋架。本研究选择五檩无梁式抬梁木构架进行研究,结构简图见图1(a)。穿斗式的特点为:沿房屋的进深方向按檩立柱,每柱上架一檩,因此穿斗式木构架的柱子排列密,更适用于尺度不大的空间。本研究选择江浙地区民居建筑常见的五檩中柱式穿斗木构架进行研究,见图1(b)。
根据以往的测绘和研究经验,考虑到本研究需对两种木框架的构件重要性进行对比分析,为更好地控制变量,设计两种典型结构形式的每榀框架檩条水平间距均为1200mm,脊檩的高度均为4547mm,上金檩的高度均为3941mm,下金檩的高度均为3341mm。开间方向共四榀间隔为3.3m的框架,形成三开间的整体结构。参考江浙地区经测绘的实际案例的构造做法,以传统民居中广泛出现的构件截面尺寸为依据,参照图1中的构件名称,设计各个构件的截面尺寸见表1。
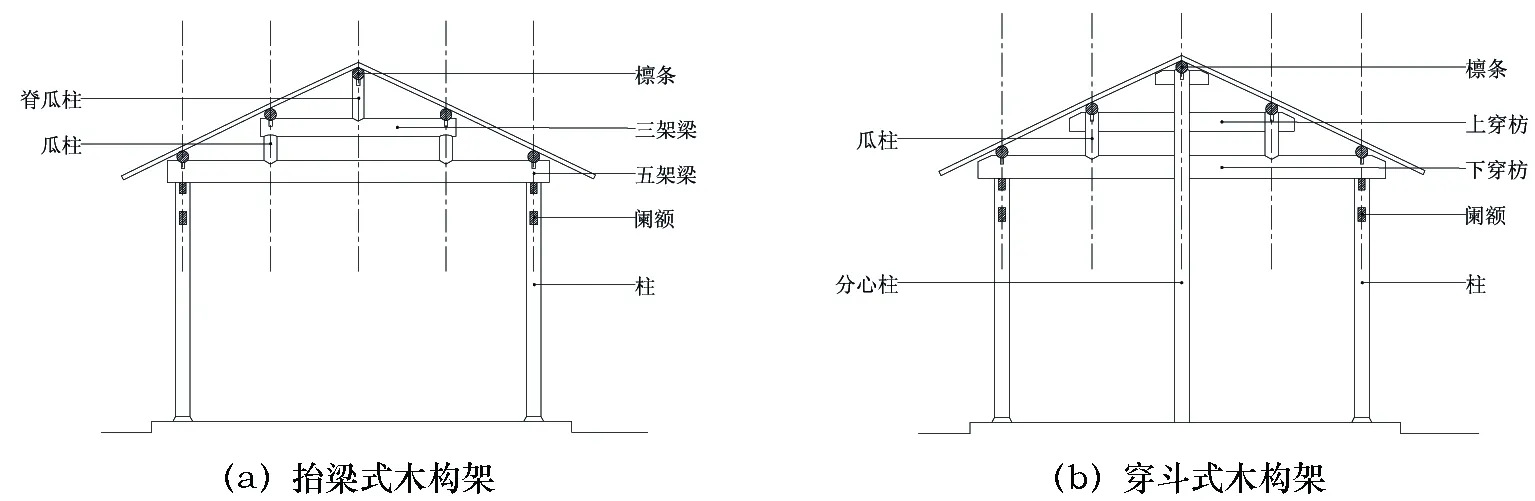
图1 传统木构建筑的结构示意图

表1 构件的截面尺寸
注: 表中d为构件截面直径。
2.2 木构架物理力学参数
运用Ansys(16.0)模拟两种典型传统木构。本研究选择江浙地区传统木构多采用的杉木作为研究材料,其属性依据以往研究的现场实测结果确定:弹性模量为6750Mpa、泊松比为0.3、密度为0.5099t/m3。本研究旨在提供适应性较广的评价结果,因此分析中假设材性均匀。当结合实际工程时,应根据木构的实际测绘结果和材性实验进行评估,如现有构件是否已经出现腐朽、裂缝、虫蛀等病害,在建模和分析时应适当降低局部材料性能以得到更精确的模拟结果。模型采用Beam189单元进行弹性运算,并将构件节点简化成刚接,柱脚简化为铰接。抬梁式和穿斗式传统木结构的有限元模型如图2。

图2 传统木构建筑的结构有限元模型
构件重要性的相对大小受荷载工况的影响,本研究考虑两种荷载工况:1)竖向荷载作用:设计屋面恒载3.5kN/m2,屋面活荷载0.7kN/m2,考虑结构自重的影响;2)水平地震荷载作用:采用底部剪力法将地震荷载简化成水平同向的节点集中力,在每个梁、柱节点处施加进深方向荷载,近似地模拟地震荷载作用,此外也考虑竖向荷载作用。
2.3 基于有限元软件Ansys的重要性评价程序开发
本研究采用有限元软件Ansys(16.0)开发了基于能量方法的生死单元法和改变弹性模量法的传统木构构件重要性评价程序,具体流程如图3所示。

图3 重要性评价程序开发流程图
2.4 计算方法的选择
根据相关文献[12-13,16-18],对于建筑结构构件的重要性分析一般采用生死单元法。生死单元作为有限元软件的一项计算功能,广泛地应用于钻孔类计算、施工过程运算、组装运算以及钢筋砼结构和砌体结构的构件重要性分析中。采用生死单元法计算时,被杀死的单元两端的变形是不连续的,并且被杀死的单元不再参与力的传递。抬梁式和穿斗式传统木构在竖向荷载作用下的生死单元法计算结果如图4所示。

图4 生死单元法重要性计算结果
根据以上计算结果云图,可以观察到在生死单元法中,江浙地区抬梁式和穿斗式传统木构的重要性计算最大值分别位于:柱与阑额相交点之上部分、脊瓜柱。抬梁式传统木构的阑额上部分柱的整体性优于下部分柱,当材料性能退化后对整体应变能的影响应当小于下部分柱,但是当构件被删除后五架梁等屋面结构都会产生较大变形,从而对应变能的影响很大,与实际的材料损伤情况存在较大差异。对于穿斗式构架,结构和荷载都是对称的,脊瓜柱损伤后只会引起脊檩的竖向位移,对其他构件没有影响,因此在抬梁式传统木构的生死单元重要性计算中脊瓜柱的重要性被明显地夸大。此外,从抬梁式传统木构的生死单元法结构整体重要性计算结果可以得到,两侧的两榀框架柱的重要性要大于中间两榀框架,而穿斗式的略小于中间两榀框架。根据经验,中间框架的受荷面积大于两侧框架,其构件损伤后对整体应变能的影响也更大,生死单元法的计算结果不能够明显地表达中间框架和边框的重要性差别。
综合考虑生死单元法的不足之处以及木构建筑的结构损伤、材料性能退化和结构的受力特征,本研究提出采用改变弹性模量法。计算时被改变弹性模量的单元的变形是连续的,且能够传递荷载,更符合传统木构建筑真实的结构状态评估。
3 传统木构单榀框架的改变弹性模量法构件重要性分析
3.1 竖向荷载作用下传统木构的构件重要性
3.1.1抬梁式单榀框架 抬梁式传统木构单榀框架的构件重要性计算结果如图5所示。图中数值反映抬梁式单榀框架的各个构件单元改变弹性模量后对结构应变能的单位体积影响能力。
本研究尝试对典型的木构形式进行构件重要性的定性排序,所得排序结果适用于相似的结构体系。在考虑竖向荷载作用的情况下,五架梁与瓜柱节点的靠柱侧位置的重要性最大,为66.116。受屋面荷载影响,上部屋面荷载通过瓜柱传递至五架梁和进而传递到柱,该节点处剪力最大。改变弹性模量后该处会产生大变形而导致屋面变形,因此对整体的变形能影响最大。受应力集中和弯矩作用影响,从该节点至柱头重要性逐渐降低。重要性系数最小的构件为脊瓜柱,对称结构在对称的屋面荷载作用下,位于结构对称轴上的脊瓜柱只产生能够影响脊檩的竖向变形,故而对整体影响小,其单位体积对整体结构的变形能影响最小,为1.308。
对于竖直构件,呈现出与以往经验相同的由上至下重要性递增的单一规律。在柱与阑额相接处出现构件重要性跃点,是受阑额的水平联系作用影响而产生的。由于阑额的作用,该节点上端柱身单元弹性模量改变后对整体柱框的影响被削弱,而对于该节点下端柱身单元,影响较上端大。对于水平构件,需同时考虑弯矩、轴力和剪力的影响。受弯矩的主要影响,三架梁和五架梁瓜柱内侧段的重要性由两侧向跨中递增;受到剪力和弯矩的共同影响,五架梁瓜柱外侧段的重要性由柱头向瓜柱递增。
依据计算结果可得抬梁式单榀框架的构件重要性的排序为:五架梁瓜柱外侧段>柱>三架梁>五架梁瓜柱内侧段>瓜柱>脊瓜柱。
3.1.2穿斗式单榀框架 穿斗式传统木构单榀框架的构件重要性计算结果如图6所示。
在竖向荷载作用下,构件重要性最大的是中柱与下穿枋节点以下的中柱部分,最大值为88.508,大于抬梁式单榀框架位于瓜柱和五架梁节点处的最大值。该部分构件传递了大部分的屋面荷载,因此改变该部分单元的弹性模量对整体结构的应变能影响最明显。在穿斗式单榀框架中,上穿枋的主要作用是控制变形而不直接参与力的传递,因此重要性最小,为0.827。中柱的存在提高了结构的刚度,弱化了下穿枋的作用,相比抬梁式传统木构将作为梁的下穿枋的跨度降低为一半,使下穿枋上的单元在改变弹性模量后对整体结构应变能的影响显著降低。在穿斗结构中竖直构件的重要性规律与抬梁结构除中柱外均相同。穿斗式结构的中柱在与下穿枋交接处出现跃点,是由于在交接处的上部分结构整体性较强,且仅承受脊檩的荷载。
依据计算结果可得穿斗式单榀框架的构件重要性的排序为:中柱(下穿枋下侧)>边柱>下穿枋 >中柱(下穿枋上侧)>瓜柱>上穿枋。
3.2 水平地震作用下传统木构的构件重要性
水平地震作用下构件重要性计算结果如图7。由于真实状态下地震荷载是水平方向往复作用的,该图仅代表水平荷载作用某瞬间的构件重要性结果。
抬梁式传统木构的重要性最大值为26.445,而穿斗式结构由于中柱的存在提高了结构刚度,其最大值为16.304,均发生在沿水平荷载方向末端柱的端头附近。对于边柱,受倾覆弯矩以及拉压变形的影响,重要性均呈现出由柱中向两端递增的规律。穿斗式传统木构的位于上穿枋和下穿枋间的中柱部位(中柱中段)的重要性很小,由于瓜柱和上下穿枋的存在,该构件附近受到的冗余约束多、刚度大。当弹性模量改变后有较多的替代传力路径,因此载荷能够被重分布到结构的其他构件上,对变形能的影响小。除了柱构件,五架梁(下穿枋)瓜柱外部分的重要性也较大,因为在水平荷载作用下梁的抗弯贡献较大。

图7 地震荷载作用下的构件重要性计算结果
依据计算结果得到模拟水平地震作用下的传统木构的重要性排序,抬梁式传统木构:柱>五架梁瓜柱外侧段>脊瓜柱>三架梁>五架梁瓜柱内侧段>瓜柱;穿斗式传统木构:边柱>中柱下段>下穿枋瓜柱外侧段>中柱上段>下穿枋瓜柱内侧段>上穿枋>瓜柱>中柱中段。
4 传统木构整体框架的改变弹性模量法构件重要性分析
4.1 传统木构整体结构重要性分析
单榀框架的构件重要性分析是基于二维空间的计算,为探究三维空间下整体结构的构件相对重要性排序,需要设计多榀框架的计算模型。参照江浙地区传统木构建筑的布局特点,本研究设计结构整体为常见的三开间木结构,两榀间均相距3.3m。两种工况作用下的抬梁式和穿斗式传统木构重要性计算结果如图8~9。
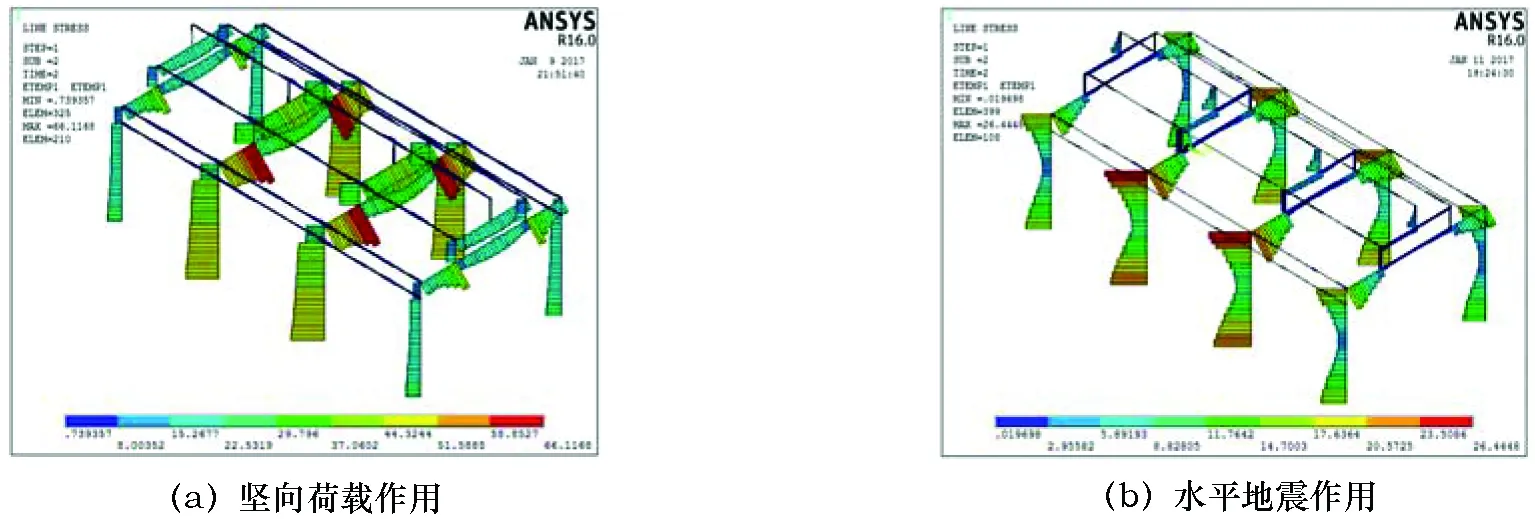
图8 抬梁式传统木构重要性计算结果
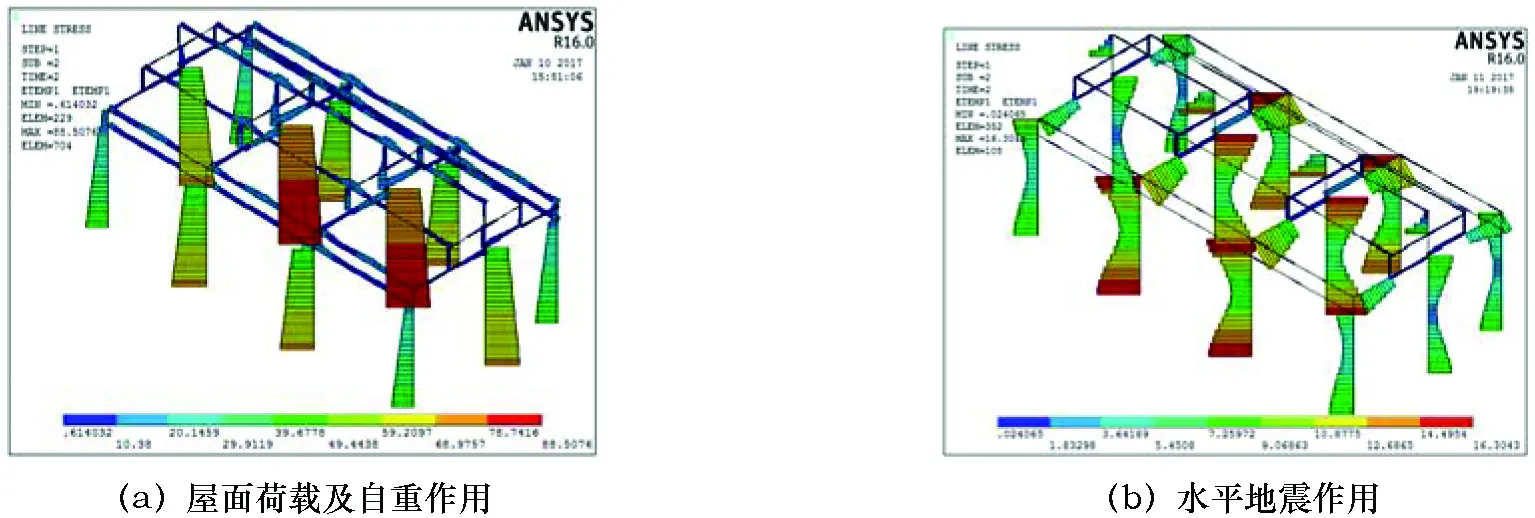
图9 穿斗式传统木构重要性计算结果
在两种工况的荷载作用下,单榀框架内部各个构件的重要性排序结果同前文中的分析,但在荷载作用下易得结构整体的中间两榀框架的重要性均大于边框。其原因是在各个工况下中间框架所承受的荷载均大于边框,当弹性模量改变时其变形的影响范围更广,对应变能的影响更大,因此与经验相符。值得注意的是各榀框架间的纵向联系构件:檩条,在图8和9中檩条的重要性均较小。一方面由于檩条的弹性模量改变后所产生的变形的影响范围小;另一方面由于结构受竖直方向以及横向水平方向的荷载作用,对于单榀框架变形几乎都是平面内的而与真实的变形情况存在些许差异,从而导致低估了檩条的重要性,而低估程度的大小还需要进一步的深入研究。
4.2 传统木构的关键区域
对传统木构构件的重要性分析需要同时考虑静力和动力荷载作用,尤其需重视其结构抗震能力。本研究建议将两种工况下重要性系数位于前10%的单元的并集作为结构的关键区域。对两种结构形式的传统木构的所有单元按照单位体积的重要性系数Γ进行排序。图10为两种木构形式的关键区域在两种工况下的叠合图,其中彩色部分为工况1即竖向荷载作用下的关键区域,黑白部分为工况2即水平荷载作用下的关键区域。

图10 关键区域分布
由图10的结果可以直观地得到抬梁式传统木构的关键区域分布于:中间两榀框架的五架梁瓜柱外侧段、近乎通长的柱;山墙面的两榀框架柱的两端较小范围区域、五架梁瓜柱外侧段的两端较小范围区域。穿斗式的关键区域分布于:中间两榀框架的中柱下段、边柱两端较大范围区域、下穿枋与柱头相接处较大范围区域、脊瓜柱与上穿枋相接处;山墙面的两榀框架的中柱下半段区域。在修缮施工和正常使用过程中,以上部位应当重点考虑和监控。
5 结 论
本研究以大型通用有限元软件Ansys为分析平台,开发了适用于传统木构的基于能量的生死单元法和改变弹性模量法的构件重要性评价程序。对抬梁式和穿斗式两种典型的传统民居木构结构类型,运用改变弹性模量法详细地分析了它们在两种工况下的构件重要性,并对两种方法进行了对比,得到以下结论:
1) 对于抬梁式传统木构,运用改变弹性模量法计算单榀框架在承受竖向荷载作用时,五架梁瓜柱外侧段的重要性最大;当承受简化的水平地震荷载作用时,柱的重要性最大。对于结构整体,同时考虑两种工况的关键区域主要分布于梁柱节点、柱脚附近。
2) 对于穿斗式传统木构,运用改变弹性模量法计算单榀框架在竖向荷载作用下时,中柱(下段)重要性最大;在水平地震荷载作用下,边柱和中柱的下段重要性最大。对于结构整体,当同时考虑两种工况时,关键区域主要分布于中间两榀框架的中柱下段和边柱柱脚、中间两榀框架的梁柱节点附近、两侧框架的中柱柱脚处。
3) 当使用有限元软件的生死单元功能计算传统木构重要性时,存在计算结果和实际损伤情况不一致的构件,并且不能够体现中间两榀框架相对于两侧框架更加突出的重要性。相比下改变弹性模量法更适用于传统木构的重要性计算分析。
4) 本研究提出的改变弹性模量的传统木构重要性评价方法计算所得的关键区域与实际工程经验基本吻合,可以为修缮、施工、结构健康监测和维护提供科学合理的理论依据。
本研究以两种简单而具有典型性的结构形式为例,对江浙地区传统民居木构构件重要性分析进行了初步探索。研究过程中存在着值得继续深入思考的问题,例如在计算中没有体现榫卯节点的半刚性特征,受计算方法限制将动力的水平地震荷载作用简化为静力问题,受荷载方向和对称结构影响低估了檩条的重要性,木材和截面属性对重要性结果的影响程度等,还有待更进一步的深入研究。
