密闭取心饱和度校正动态模型及影响因素分析

涂彬 李杰

中国石油大学（北京）油气资源与探测国家重点实验室

0 引言

探井与开发井储层含油饱和度分析是评价油藏潜力和开发效果、制定开发方案与调整方案等的重要依据和基础［1］。求取地层含油饱和度的方法很多：李宝同应用测井方法求取地层油水饱和度［2］；Botset［3］（1939）和 Rathmell［4］（1973）等利用常规岩心方法分析水驱油藏的剩余油饱和度；贾振尧（1995）等分析比较了常规密闭岩心与保压密闭取心分析方法［5］，和李万顺［6］、马力宁［7］等人得到了比较一致的认识，都认为常规密闭取心法相对准确、直观与经济，在国内应用很广泛，为油田勘探开发研究试验提供了可靠的油层物性数据，但他们也发现利用常规密闭取心方法测量的油水饱和度之和一般都小于100%，有的甚至低至70%以下，说明常规密闭取心法存在比较明显的误差，需要进行校正，才能得到真实的地层流体饱和度。

针对常规密闭取心存在的精度不足，目前有4种类型的饱和度校正方法，即校正系数法、室内实验法、数理统计回归法和数学模型校正法。Rathmell在文献［3］中首先提出了校正系数法，Kazemi［8］（1977）和 Emmanuel［9］（1997）等人在此基础上提出了不同的校正系数值。这类方法比较简单，考虑的因素较少，校正得到的饱和度与实际相比误差较大。杨胜来［10］（2004）、张亮［11］（2009）和刘丽［12］（2009）等人采用室内实验法对岩心饱和度进行校正，叶青（2016）进行了长岩心水驱油标定饱和度损失［13］。这些实验的过程比较类似，都是通过高压下配制带有溶解气的实验用油，然后降压脱气，测量脱气前后水饱和度并回归得到二者的关系式。该方法应用时不用描绘降压脱气过程中复杂的物理化学变化过程，但复配地层油气水组成及含量存在误差。马名臣等（1993）统计江苏油田密闭取心数据，发现油水饱和度间存在线性关系，提出了数理统计校正方法［14］，王艺景等（2000）引入曲线平移和旋转对该方法进行了修正［15］；孙佩等（2012）在应用该方法时先对不同孔隙结构的岩心进行分类，然后再进行校正［16］。这些操作本质上是对一定量的测试饱和度数据进行统计回归分析，因此归类为数理统计回归法。该方法比较简单、容易理解，但未考虑岩心和流体性质的差异性和取心过程中状态变化，统计得到的损失率受不同岩石性质的影响，样本点的归类标准不客观，存在较大的误差。辛治国（2012）基于流体分流率原理提出了密闭取心校正数学模型［17］，程会明（2012）建立了类似的模型［18］，王玉环（2014）采用指数函数处理辛治国和程会明模型中的水油相渗比［19］，总体上这3种模型的形式和求解方法基本不变。马勇新（2016）引入了应力敏感效应推导了一种新的密闭取心饱和度校正模型，相对前面3种模型有了改进，但其本质仍然没有改变，模型仅考虑了油和水的分流率却没有考虑溶解气的影响［20］。总体来看，现有的数学模型方法考虑了从地下到地面后岩心孔隙体积和流体体积的改变，并基于分流理论来确定取心过程中流体的变化，但存在2个问题：一是仅仅考虑了从地下到地面这2个状态下岩心孔隙体积变化和流体变化，没有考虑整个压降过程；二是没有考虑取心时油气溶解与分离的整个过程，只考虑了地面条件下岩心饱和度的分布结果，没有体现出压力下降过程中各种参数的变化过程。

基于目前研究方法及存在的问题，本文将建立一种动态校正模型，同时考虑岩心上提过程中因压力不断下降导致的孔隙形变和油气分离逸散，以获得较精确的密闭取心饱和度动态校正结果。

1 密闭取心饱和度动态校正模型

1.1 密闭取心饱和度影响因素

文献［17-19］中，辛治国和王玉环等人综合大量的研究成果指出，密闭取心测量的油水饱和度受到5个方面的影响：（1）岩石孔隙体积变化和流体体积变化；（2）岩心内的原油降压脱气，出现溶解气驱；（3）岩心至地面后转运过程中油水的挥发；（4）钻井取心时钻井液入侵；（5）实验误差。

文献［17］中辛治国指出这5个因素中，实验误差无所不在，钻井液侵入和岩心转运过程也不是很重要的影响因素，因此不做重点考虑。综上所述，密闭取心岩心饱和度的主要影响因素是岩心上提过程中岩石孔隙体积变化、流体体积变化和溶解气驱替，因此对这3种影响因素的校正也是众多研究关注的重点问题。一般来说，这3个因素受温度和压力影响较大，而密闭取心在上提至地面时，由于时间较短，岩心筒内的温度变化幅度较小，压力变化比较明显，因此压力的改变是导致岩心内流体饱和度变化的主要原因，所以文中重点是分析压力变化导致的饱和度变化。

1.2 取心过程油水饱和度动态变化

在上提过程中，压力持续不断下降，岩心内的流体饱和度也是持续不断变化的，这是一个动态的连续过程。可以基于离散原理将一个连续的物理过程用有限个阶段过程来近似表示，即可以将岩心上提过程中连续的压力变化用阶段压力来替代，每降低Δp，岩心内的流体会出现如下的变化。

（1）压力变化Δp后，如果岩心筒内的压力高于饱和压力，则岩心内只有孔隙体积和液体体积发生变化。在这二者的综合作用下，岩心内的液体被排挤出来，从而导致岩心内流体饱和度的变化，此时排挤出来的油水体积可认为是按照油水分流量分配。

（2）如果压力变化Δp后，岩心筒内的压力低于饱和压力，此时会出现溶解气分离现象，因此除了液体膨胀、孔隙体积缩小之外，溶解气也会膨胀且体积变化幅度更大，从而被排挤出来的流体体积更多，岩心内流体体积的变化幅度也更大一些。

随着岩心筒的继续上行，筒内压力进一步下降。岩心筒内的饱和度变化会重复上述（1）或（2）的过程，当压力比饱和压力低得多时，气体析出量增加，成为连续相，因此气体更多的是逸出岩心，且携带液体流出岩心，表现出比较明显的溶解气驱的特征。

1.3 密闭取心饱和度多相流体的校正方程

油气两相渗流或者是油气水三相渗流的过程是不稳定的，但在总过程中每一瞬间可近似看成稳定状态，这样，总过程的不稳定状态就可以看成是无数个稳定状态的叠加，这种方法称为稳定状态逐次替换法（引自葛家理［21］（1982））。当时间间隔或者压力间隔取得很小时，用此方法求得的结果将基本符合实际情况。注水开发油藏压力一般大于其饱和压力，岩心上提时压力下降可分为泡点压力之上和之下2个阶段，因此在进行饱和度校正时应对这2个阶段分别进行考虑。

1.3.1 岩心压力在泡点之上的校正方程 当压力下降，如果岩心压力大于泡点压力，溶解气不分离，此时液体膨胀和岩石孔隙体积压缩导致流体被排挤出来的流体总量为

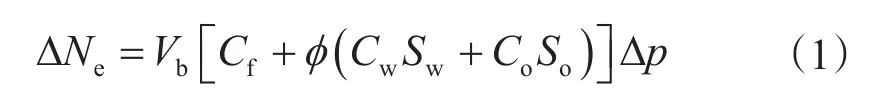
按照物质平衡原理，岩心降压后剩余油量为降压前油量与被排挤的油量之差，且认为被排挤出来的油水的量按照分流量方程分配，因此可以得到

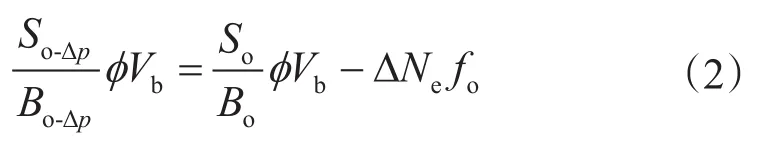
将式（1）中的总液量ΔNe带入式（2）并化简可以得到

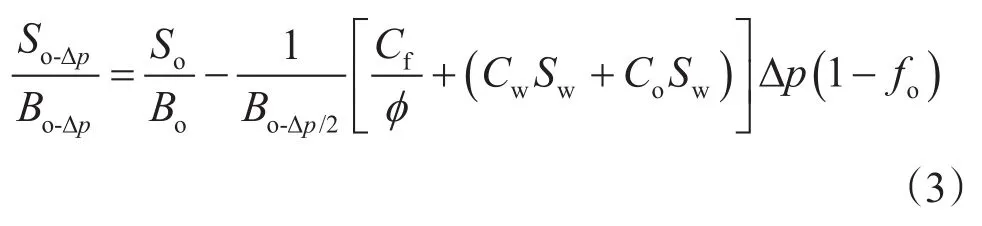
其中，fw是含水率，按照分流量方程有

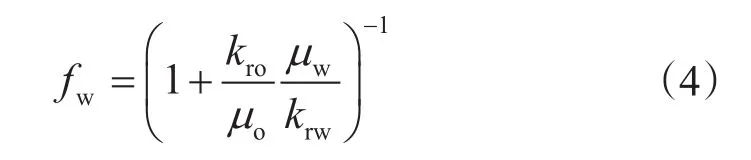
式（4）中kro和krw关于饱和度的函数，此时对应的饱和度应为降压之前和之后的平均饱和度：Sw=（Sw+Sw-Δp）/2。考虑到此时只有油水两相，Sw+So=1，因此式（4）是一个关于饱和度Sw-Δp的隐函数方程，可以采用迭代法的方式求解得到Sw-Δp。

1.3.2 岩心压力在泡点之下的校正方程 当压力下降后，如果岩心压力小于泡点压力，出现溶解气分离，此时气体膨胀、液体膨胀和岩石孔隙体积压缩导致流体被排挤出来的流体总量ΔNe为

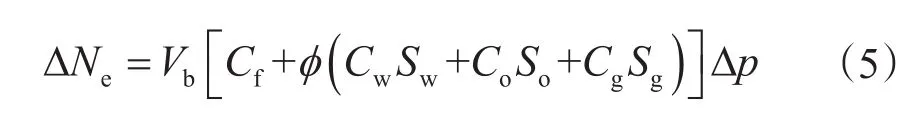
降压比较小的时候，近似认为在岩心内的渗流是稳定渗流，因此被排挤出岩心的油气水三相可近似按照分流量fw、fo、fg来分配。

油组分的物质平衡原理为：岩心降压后剩余油量=降压前油量-排出油量，由此可知油饱和度的校正方程为

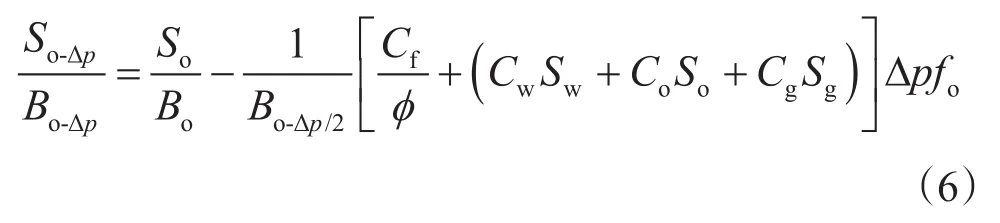
同理可知水饱和度校正方程为

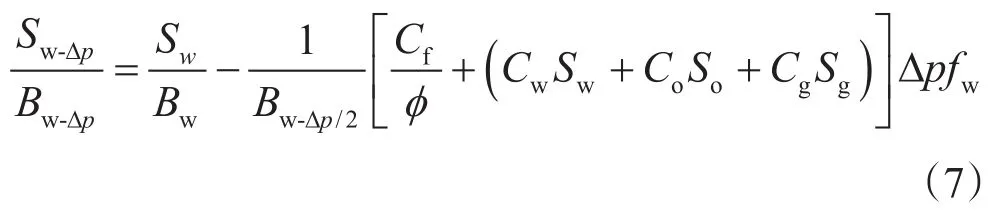
气组分的物质平衡原理为：降压后游离气量=降压前游离气量+降压前溶解气量-降压后溶解气量-排出气量，因此可以得到气体饱和度校正方程为

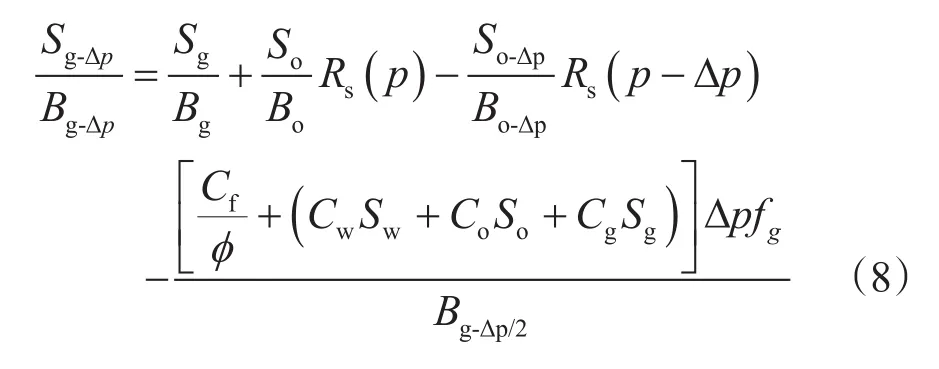
在上面的3个校正方程中，油水气三者的分流量fw、fo、fg的表达式分别为

1.4 岩心测试饱和度校正的计算流程

根据岩心上提过程中油水饱和度变化的过程分析，可以采用图1的流程来拟合实际岩心测试的饱和度。

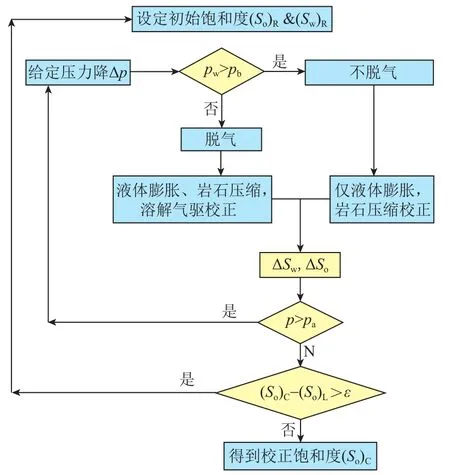
图1 岩心测试饱和度校正的计算流程图Fig. 1 Calculation flow diagram of measured core saturation correction

（1）设定初始的油藏饱和度，如果注水开发油藏地层压力高于饱和压力，则可以得到Sg=0；

（2）降低压力，判断此时岩心筒内的压力是否低于泡点压力，如果高于泡点压力，则只需要根据油水两相流来校正岩心饱和度的变化；如果低于泡点压力，则岩心内流体脱气，出现溶解气驱，此时需要用三相流来校正岩心饱和度的变化。

（3）计算降压后的岩心饱和度，如果岩心筒内的压力仍然高于大气压或者至地面给定参考压力，则继续降低压力，用此时计算的岩心饱和度替代初始饱和度，重复（2）的过程直至岩心筒内的压力降低至给定参考压力。

（4）将计算得到的地面压力条件下的岩心饱和度与实验测试的岩心饱和度进行比较，判断这两个数值之间的差值是否满足误差要求，如果满足则说明初始给定的饱和度就是要寻求的油藏饱和度，反之则重新给定一个初始饱和度进行计算。重复（1）～（4）的过程，直到满足误差为止。

2 岩心饱和度随压力变化及参数敏感性分析

2.1 岩心相关参数

密闭取心测量饱和度之后，根据建立的动态模型进行校正，校正过程中，所需相关参数：地层水体积系数Bw为1.020，地层水黏度为0.304 mPa·s。地层油和天然气的高压物性数据见表1，包括原油黏度、天然气黏度、原油体积系数、天然气体积系数及溶解气油比。

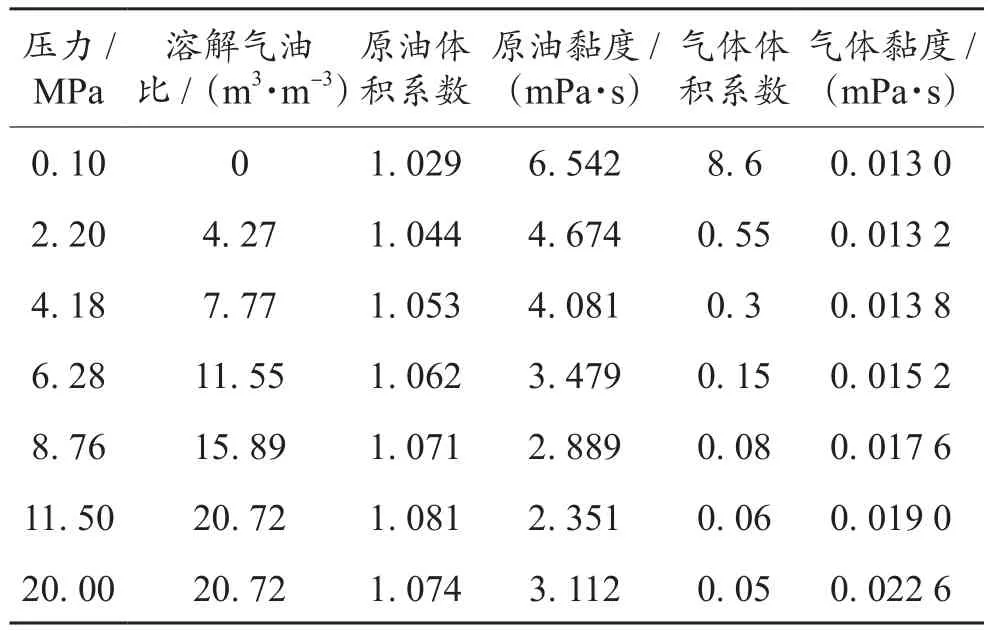
表1 油藏区块PVT数据Table 1 PVT data of oil reservoir

图2为原油和水的两相相渗曲线，图3为天然气和液体的两相相渗曲线。三相相渗可根据这2组相渗曲线应用Stone I模型［22］计算得到（此处略）。

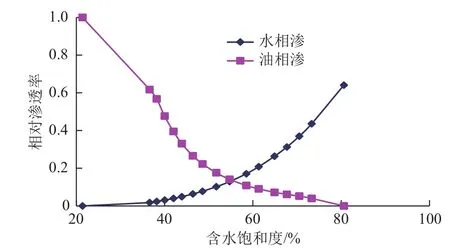
图2 原油与水的相对渗透率曲线Fig. 2 Oil/water relative permeability curve

2.2 取心过程油气水三相饱和度变化特征

利用油田取得的油藏性质、岩石及流体物性资料，结合图2、图3的相对渗透率数据对岩心取心过程中的饱和度变化进行计算。地层压力为13.5MPa，饱和压力为11.5 MPa，地层原油黏度为2.7 mPa·s。假设初始油水饱和度分别为50%和50%，采用本文模型（见1.4计算过程①～③）计算的结果可再现油气水三相饱和度损失的过程，结果如图4所示。

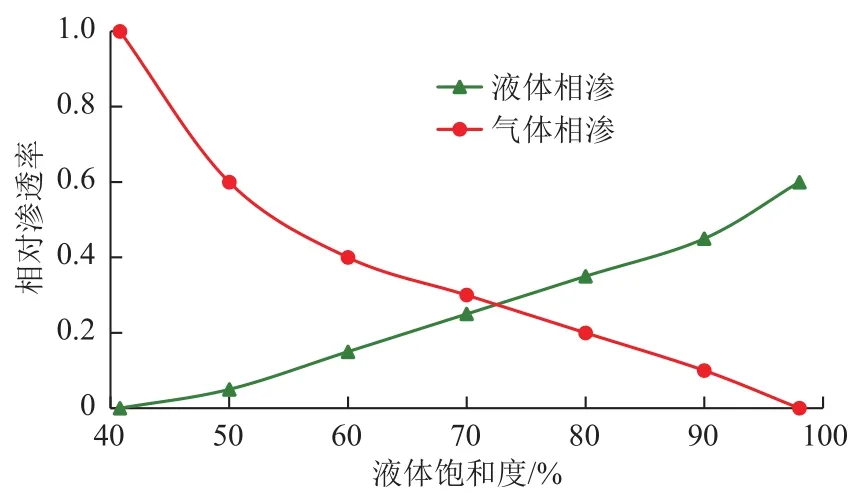
图3 天然气与液体的相对渗透率曲线Fig. 3 Gas/liquid relative permeability curve

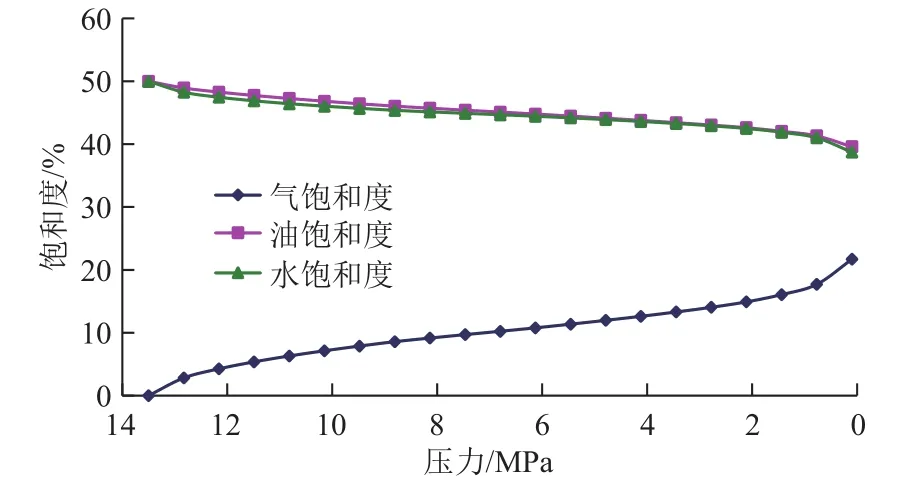
图4 半解析饱和度校正计算结果Fig. 4 Calculation result of semianalytical saturation correction

从图4可以看出，随着压力的降低，岩心气体饱和度迅速增加，而油和水的饱和度相应降低。这说明气体在膨胀过程中，会将一部分原油和水从岩心中排挤出去。当岩心压力降低至地面大气压时，气体饱和度约为22%左右，原油的损失量约为10%，水的损失量约为11%。

2.3 密闭取心饱和度影响因素敏感性评价

根据实际油藏的参数，对影响密闭取心饱和度的因素进行了敏感性分析，方案设计为：以基本参数为基准值，通过曲线平移或拉伸等方法，使每个影响因素分别增加或减少30%、20%、10%，这样每个影响因素共计算7个方案。计算结果见图5和图6，图中横坐标为各影响参数的变化幅度，纵坐标分别为剩余在岩心中油水饱和度。

从图5和图6可以看出每个因素的影响程度，并得到以下6个方面的认识。

（1）气体黏度对岩心油水饱和度的影响最大。泡点时气体黏度从比基准值小30%增加至比基准值大30%时，岩心油饱和度减少3.3%，岩心水饱和度减少2.3%，岩心综合油水饱和度改变率为9.3%。说明气体黏度越高，溶解气运移携带油和水的能力越强。其中，岩心综合油水饱和度改变率=（岩心油饱和度改变值+岩心水饱和度改变值）÷对应参数变化幅度百分比×100%。

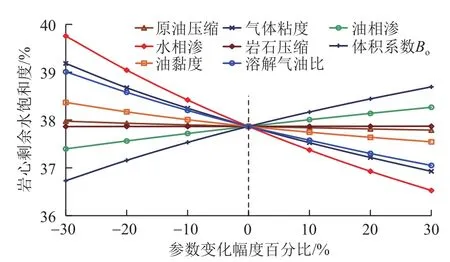
图5 岩心相关参数变化与含油饱和度关系曲线Fig. 5 Relationship of variation of core parameters vs. oil saturation

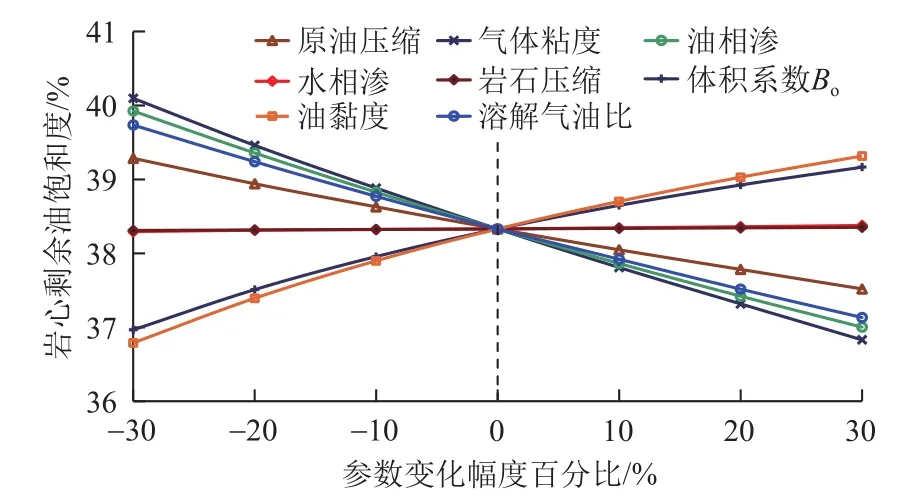
图6 岩心相关参数变化与含水饱和度关系曲线Fig. 6 Relationship of variation of core parameters vs. water saturation

（2）溶解气油比对岩心油水饱和度的影响较大，且对岩心油水饱和度的影响并不是线性增加。当泡点时溶解气油比从比基准值小30%增加至比基准值大30%时，岩心油饱和度减少2.6%，岩心水饱和度减少2.0%，岩心综合油水饱和度改变率为7.6%。

（3）原油体积系数对岩心油和水的饱和度影响程度也都比较大，原油体积系数越大，岩心中的油和水饱和度越高。当泡点时原油体积系数从比基准值小30%增加至比基准值大30%时，岩心油饱和度增加2.2%，岩心水饱和度增加2.0%，岩心综合油水饱和度改变率为6.9%。由于此处设计的情形可能导致原油体积系数小于1，因此计算结果仅具参考意义。为确保体积系数大于1，本文考虑了原油体积系数从比基准值小3%增加至比基准值大3%的情况，计算结果显示，此时岩心油饱和度改变0.25%，岩心水饱和度改变0.2%，岩心综合油水饱和度改变率为7.5%，和6.9%相差不大。

（4）原油黏度对岩心油饱和度的影响比对岩心水饱和度的影响大许多。当泡点时原油黏度从比基准值小30%增加至比基准值大30%时，岩心油饱和度增加2.5%，而水饱和度减少0.8%，岩心综合油水饱和度改变率为5.5%。说明油黏度越大，岩心油饱和度越高，被溶解气携带出来的水越多。

（5）相渗对岩心油水饱和度的影响也各不相同，油相渗对岩心油饱和度的影响更大，水相渗对岩心水饱和度的影响更大。当油相渗从比基准值小30%增加至比基准值大30%时，岩心油饱和度减少2.9%，水饱和度增加0.9%，岩心综合油水饱和度改变率6.3%；当水相渗从基准值的-30%增加至30%时，岩心油饱和度仅增加0.1%，水饱和度却减少3.2%，岩心综合油水饱和度改变率为5.5%。

（6）压缩系数对岩心油水饱和度的影响不大。其中岩石压缩系数的影响最小，当岩石压缩系数从比基准值小30%增加至比基准值大30%时，岩心油水饱和度的变化值都不超过0.1%；原油压缩系数仅对岩心油饱和度有影响，当原油压缩系数从比基准值小30%增加至比基准值大30%时，岩心油饱和度减少1.8%，水饱和度仅减少0.2%，岩心综合油水饱和度改变率为3.3%。

综合各参数的影响程度，可以认为取心过程影响岩心饱和度变化的参数排序为：气体黏度、溶解气油比、原油体积系数、原油黏度、油水相渗和原油压缩系数，影响最小的是岩石压缩系数。

3 密闭取心饱和度动态校正模型验证

3.1 油藏简况

国内西部某油田区块，埋藏深度1 380 m左右，油层有效厚度约30 m，原始地层压力13.7 MPa，饱和压力11.4 MPa，地饱压差2.3 MPa，原始含油饱和度平均为60%左右。该油藏以细砂岩、粉砂岩及中砂岩为主，孔隙度14.9%～12.5%，平均13.9%，渗透率10～27.2 mD，平均 15 mD。

3.2 密闭取心饱和度校正结果评价

W400217井地层水饱和度来自于生产单位，是基于岩心资料获取相关饱和度计算参数，而后根据测井评价方法对岩心四性参数进行标定求取的流体饱和度值，和文中提供的动态模型计算结果进行比较，结果如图7所示，可以看出，密闭取心饱和度经过模型校正后，与标定饱和度的相对误差范围平均为0.8%，和静态模型［17］计算结果（相对误差平均为1.8%）相比，与标定饱和度更接近，说明文中提供的动态校正方法具有一定可信度。从动态模型的建立和计算过程来看，本文模型在2个方面取得了进展：其一是考虑了取心过程中压力的动态变化过程，更符合饱和度变化的实际情况；其二是同时考虑孔隙体积变化和流体体积变化，更符合取心过程中岩心的相态变化规律。

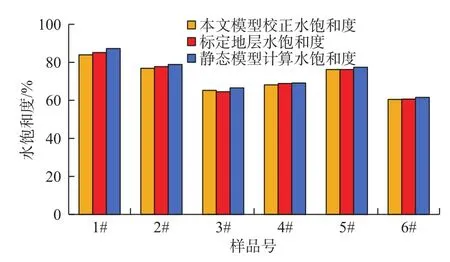
图7 W400217井含水饱和度测试及校正结果Fig. 7 Water saturation measured in Well 400217 and its correction result

4 结论

（1）密闭取心过程中，岩心内流体饱和度变化是动态过程，孔隙和油水体积、原油脱气等随着压力降低持续不断变化，这是造成密闭取心测试饱和度出现误差的根本原因，因此需要针对这些因素进行饱和度校正。

（2）基于稳定状态逐次替换原理和多相流分流量理论，建立了岩心油水饱和度动态校正数学模型。模型既考虑了压力的动态变化过程，又将取心过程中孔隙体积和流体体积这二者的状态变化过程同时进行计算，更加符合取心时岩心中的相态变化规律。

（3）参数敏感性分析结果表明，溶解气对岩心油水饱和度的影响都比较大，气体黏度从标准值的-30%增加至30%时，油水饱和度一共减少5.6%；溶解气油比对应的油水饱和度共减少4.6%。原油体积系数的影响程度次之，该参数从-3%增加3%时，油水饱和度共增加0.45%左右。原油黏度和油相渗透率仅对岩心油饱和度影响较大，而水相渗仅对岩心水饱和度影响较大。岩石压缩系数对岩心油水饱和度的影响较小，影响程度不超过0.1%。综合而言，影响程度大小排序依次为：气体黏度、溶解气油比、原油黏度、原油体积系数，油水相渗和原油压缩系数，影响最小的是岩石压缩系数。

符号说明：

Bo为原油体积系数；Bo-Δp、Bw-Δp、Bg-Δp分别为压力下降时，压力下的油、水和气的体积系数；Bo-Δp/2、Bw-Δp/2、Bg-Δp/2分别为压力下降时，压力区间平均压力下的油、水和天然气的体积系数；Cf、Co、Cw分别为岩石、地层原油、地层水体积压缩系数，MPa-1；fo、fw、fg分别为含油率、含水率和含气率，%；kro、krw、krg分别为油、水和气的相对渗透率；Rs为地层原油溶解气油比，m3/m3；So、Sw、Sg分别为含油饱和度、含水饱和度和含气饱和度，%；Swc、Sor分别为束缚水饱和度和残余油饱和度，%；Vb为岩石外观体积，m3；μo、μw、μg分别为油、水和气的黏度，mPa·s；φ为孔隙度，%。