基于矩阵指数的点云配准方法

杨正世，李文国

(昆明理工点大学机电工程学院，云南 昆明 650500)

0 引言

点云配准技术是研究不同视角，即不同参考坐标下的一组点云或多组点云。通过某种算法，将具有一定重叠度的点云数据，通过平移旋转缩放等操作变换到同一参考坐标系下，进而得到实体完整的点云数据信息[1]。它是整个三维点云数据处理中的关键步骤，不但为后期的点云数据建模提供了较为精确的点云数据，而且为构建高精度的模型提供了保证。该技术广泛应用于3D游戏[2]、物体识别[3]、大坝测量[4]、文物保护[5]、医疗矫形[6]、机器人点位导航及自动地图构建[7-8]等领域。

点云配准的关键在于求取变换矩阵。目前常用的点云配准算法，是由Paual J和Besl[9]在1992年提出的最近点迭代(iterative closest point,ICP)算法以及基于ICP算法的改进算法。点云配准优化问题，可以转化为求取一个有6个自由度的刚体变换M(R,T)，将两片点云配准到同一坐标系下，使配准点云之间的距离误差达到最小。ICP算法对初始点云对的对齐要求非常高。如果初始点云对未能对齐，将会使ICP算法陷入局部最优。初始点云对对齐，将减少迭代的次数，提高点云配准的速度和精度。

目前，求解位置变换矩阵的主要方法如下。Beltrami和Jordan提出的奇异值分值(singular value decomposition，SVD)[10]法，求解的变换矩阵精度高，但是需多次迭代，会影响点云配准的速度。文献[11]对Horn[12]提出的四元素表示法进行了细致的描述。列文伯格-马夸尔特法(Levenberg-Marquardt,LM)[13]算法能够借助高斯-牛顿算法以及梯度下降法的优点，并对两者的不足之处作了改善;但是其局部搜索耗时大，求得的变换矩阵精度不高。因此，本文提出了一种基于矩阵指数表示变换矩阵的点云配准方法，从而提高求取变换矩阵的速度和精度，以及ICP算法的收敛速度和计算精度。

1 算法描述

1.1 目标函数

如前文所述，点云配准优化问题，可以转化为求取一个有6个自由度的刚体变换M(R,T)，将2片点云配准到同一坐标系下，使配准点云之间的距离误差达到最小。假设待配准点云集P={p1,p2,…,pi}，1≤i≤n},Q={q1,q2,…,qi}，1≤i≤m。其中：n、m分别为P和Q中点云的总数。用R表示旋转变换矩阵，T表示平移变换向量，则ε(R,T)表示源点集Q在变换矩阵M(R,T)的作用下与目标点集P之间的误差。因此，求解点云配准优化的问题就可以转化为求解满足 min[ε(R,T)]的最优解，可以定义为：

(1)

式中:qi为点云集Q中的一个点云数据；pi为点云集P中的一个数据点；R∈SO(3)；T∈R3。

假如(pi，qi)为对齐的点云对，ni为它们之间单个点云的法向量，如需确定最佳的变换矩阵M(R,T)，以实现点云集P和点云集Q配准，则可将式(1)变换为：

(2)

式中：ni为点云qi点的法向量；(piR+T-qi)为点云pi到点云qi的一种线性转换；[(piR+T-qi)ni]2为piR+T点到qi平面距离的平方。

1.2 求解变换矩阵

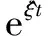
(3)

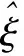
(4)

由指数ex展开可知，当|x|<1时，ex≈1+x。所以，当坐标旋量‖ω‖<1时，式(4)可以表示为：

(5)

T=v

(6)

将式(5)和式(6)代入式(2)，可得：

(7)

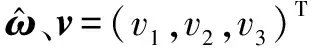
定义a=P×n，则式(2)可以重写为：

(8)

要使式(8)有最小值，则要先求取函数ε(R,T)关于ω和v参数的偏导数。当偏导数为零，即可求出参数的值。求解偏导公式为：

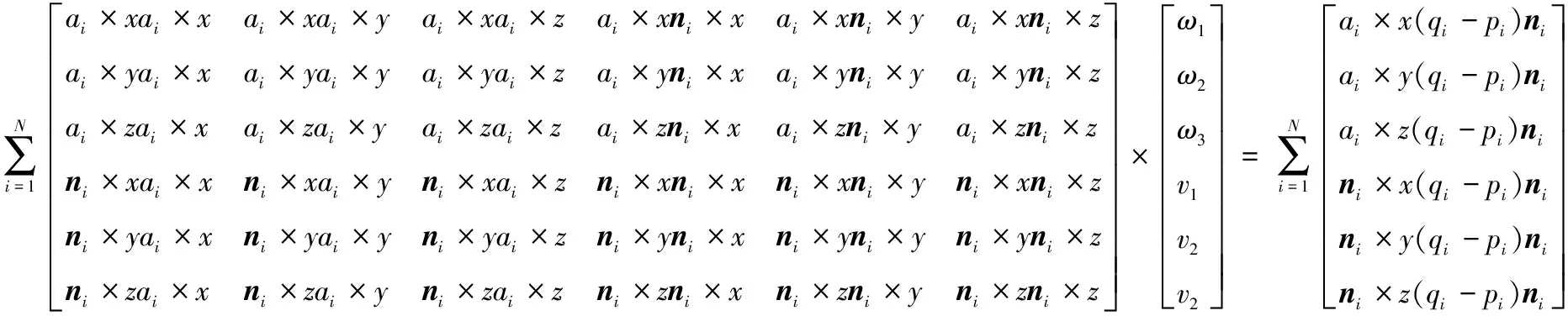
(9)

将式(9)表示为Ax=b的线性矩阵方程。其中：A为6×6的协方差矩阵，可以用已知的ai和ni表示；x为6×1的未知向量；b为6×1的向量，可以通过对应的点云对(pi，qi)和ai和ni表示。求解Ax=b的线性矩阵方程，就可以得出旋转矩阵R和平移向量T，即完成变换矩阵求解。从式(9)可知，求解变换矩阵只需要6个方程，算法易于实现，且不需要构造其他的模型函数。在LM算法中，需要构造模型函数f，并在其领域内对估计参数向量p作线性近似变换。如未能较好地构造模型函数构，将直接影响变换矩阵的求解。在SVD算法中，需要计算点云的质心，然后构造协方差矩阵。该方法计算量大，迭代次数多。从式(9)可以看出，本文方法很好地避免了上述两种算法的不足，能够快速、精确地求出变换矩阵。

1.3 点云配准

为了加快对点云对(pi，qi)最近点的搜索，采用K-D tree搜索法来寻求最近点，提高整体的点云配准速度。如前文所述，ICP算法对初始位置对齐的点云对依耐性较高。采用随机采样一致性算法(random sample consensus，RANSAC)[15]去除错误的点云，以减少计算迭代的次数，并结合本文算法来求出变换矩阵，完成点云配准。 具体的点云配准流程如图1所示。

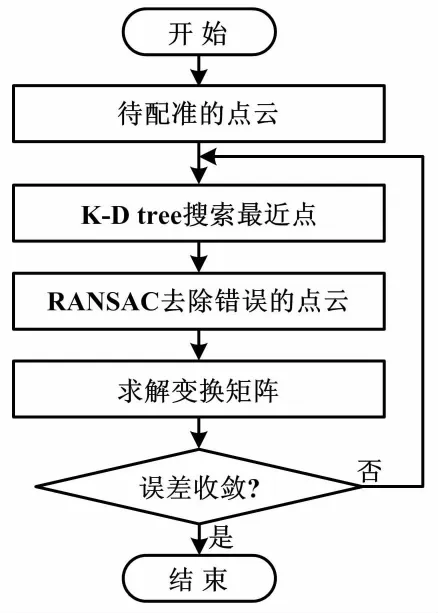
图1 点云配准流程图

2 试验结果与分析

2.1 试验评估及试验环境说明

试验从以下2个方面进行评估。

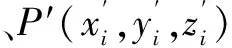
②在相同的条件下，分别与基于SVD算法的ICP算法和基于LM算法的ICP算法，比较配准的精度和配准的运行时间。

本文所有试验的计算机配置为：AMD A8 2.1 GHz CPU、4 GB内存，WIN7 64位操作系统。点云配准方法采用C++语言在Visual 2010上编程实现，并调用PCL 1.7.2版本[16]的点云库显示和保存点云。

为了验证本文方法的有效性，试验中的点云数据采用斯坦福大学提供的Bunny、Happy和Dragon数据样本。数据大小分别为：35 947个Bunny数据，32 328个Happy数据，22 998个Dragon数据。

2.2 配准的结果展示

2.2.1 Bunny配准结果

将Bunny的点云数据分别代入基于SVD算法、LM算法以及本文方法。3种算法各自迭代30次，Bunny点云配准的结果如图2所示。

图2 Bunny点云配准结果

从图2可知，本文方法和SVD算法优于LM算法。在Bunny的耳朵处，LM算法配准得不是很好，出现大量的不配准点。为了客观地表示Bunny点云配准的结果，分别对上面3种算法迭代不同的次数，比较其配准时间和配准精度，结果如表1所示。

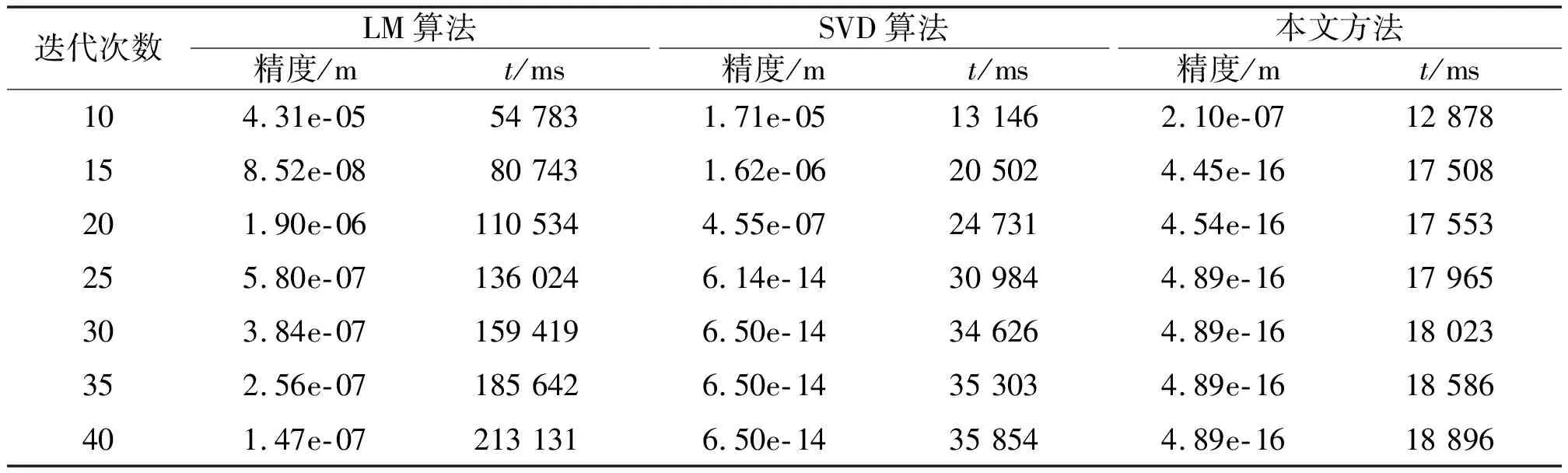
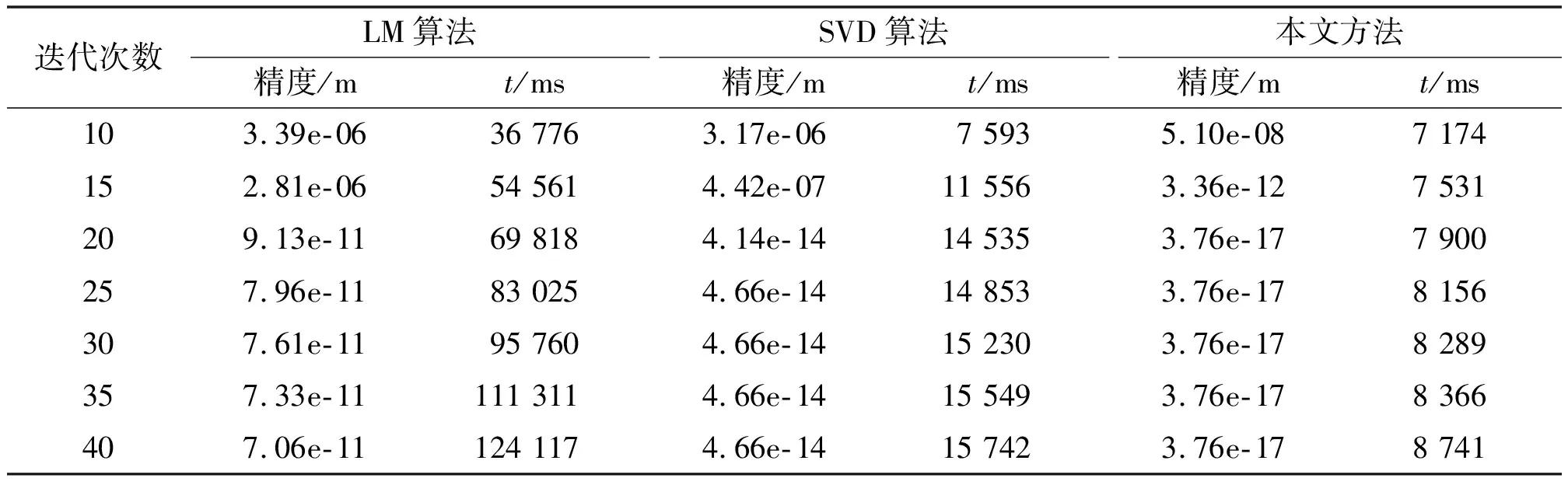
表1 Bunny点云配准精度和时间对比

从表1可以得出,本文方法配准精度和速度明显优于LM算法和SVD算法。LM算法在迭代15次时配准精度出现最高，精度数量级达到10-8；在迭代20次时精度降低，然后随着迭代次数的增加精度提高。SVD算法在迭代30次时达到局部最优，得到最佳的匹配，精度数量级达到10-14。本文方法在迭代15次时，精度数量级达就到10-16，明显超过其他2种算法的最佳配准精度数量级。在3种算法分别迭代40次时，LM算法在速度上是最慢的，本文方法最快，所用时间是SVD算法所要时间的6倍、LM算法的11倍。很明显，本文方法在速度上明显优于其他2种算法。

2.2.2 Happy配准结果

将Happy的点云数据分别代入3种算法。3种算法各自迭代30次的配准结果如图3所示。

由图3可知，本文方法和LM算法优于SVD算法。SVD算法在Happy的上部分右边处配准得不是很好。

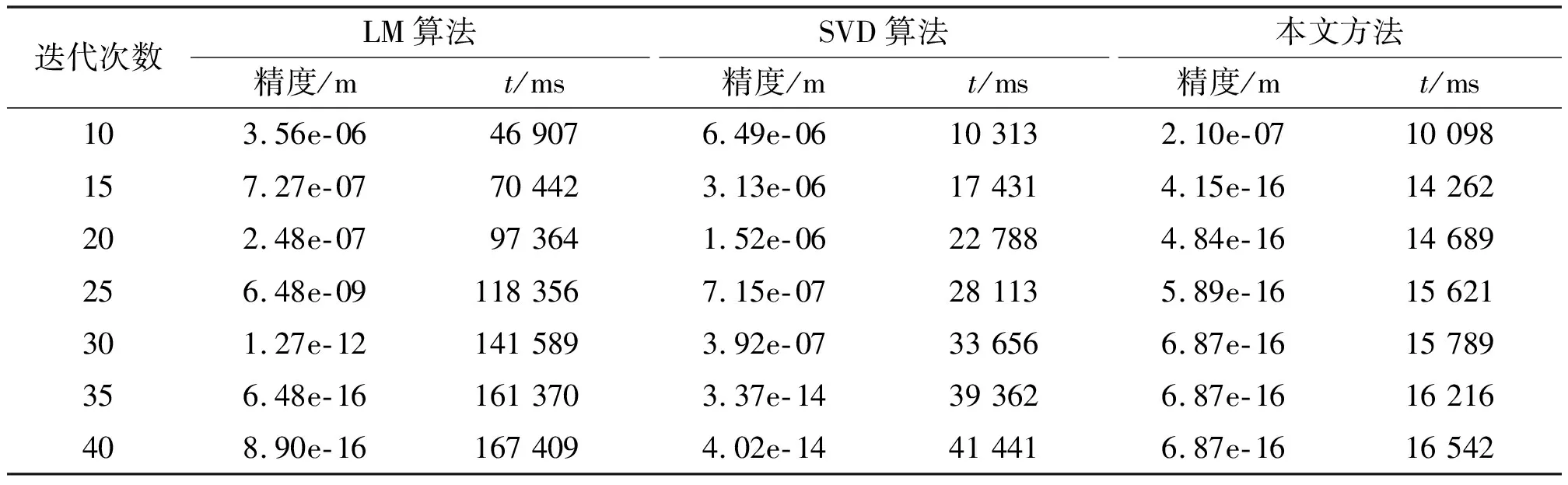
同样地，为了客观表示Happy点云配准的结果，分别对3种算法迭代不同的次数，比较其配准时间和配准精度，结果如表2所示。

图3 Happy点云配准结果

迭代次数LM算法精度/mt/msSVD算法精度/mt/ms本文方法精度/mt/ms103.56e-0646 9076.49e-0610 3132.10e-0710 098157.27e-0770 4423.13e-0617 4314.15e-1614 262202.48e-0797 3641.52e-0622 7884.84e-1614 689256.48e-09118 3567.15e-0728 1135.89e-1615 621301.27e-12141 5893.92e-0733 6566.87e-1615 789356.48e-16161 3703.37e-1439 3626.87e-1616 216408.90e-16167 4094.02e-1441 4416.87e-1616 542

由表2可知，LM算法从迭代初始次数时配准精度就高于SVD算法，在迭代40次时配准精度高于本文方法。但是，本文方法收敛速度仍然是3种算法中最快的。在迭代15次时，本文方法精度数量级达就到10-16、LM算法精度数量级为10-7、SVD算法精度数量级为10-6，证明本文方法配准精度远高于其他2种算法。在配准时间上，LM算法总大于SVD算法和本文方法。LM算法迭代10次所花时间大于SVD算法迭代40次的时间，本文方法的配准时间仍然是最小的，明显小于其他2种算法。

2.2.3 Dragon配准结果

将Dragon的点云数据分别代入3种SVD算法。3种算法各自迭代30次，Dragon点云配准结果如图4所示。

从图4可知，3种算法的配准效果都较好。同样地，为了客观表示Dragon点云配准的结果，分别采用上面3种算法迭代不同的次数，比较其配准时间和配准精度，结果如表3所示。

图4 Dragon点云配准结果

迭代次数LM算法精度/mt/msSVD算法精度/mt/ms本文方法精度/mt/ms103.39e-0636 7763.17e-067 5935.10e-087 174152.81e-0654 5614.42e-0711 5563.36e-127 531209.13e-1169 8184.14e-1414 5353.76e-177 900257.96e-1183 0254.66e-1414 8533.76e-178 156307.61e-1195 7604.66e-1415 2303.76e-178 289357.33e-11111 3114.66e-1415 5493.76e-178 366407.06e-11124 1174.66e-1415 7423.76e-178 741

由表3可知，从精度上看，LM算法是3种算法中最差的一种，在迭代次数超过25次时收敛几乎保持不变，在整过迭代过程中没有出现局部最优值； SVD算法在迭代20次时超过LM算法，在迭代25次时出现局部最优值；本文方法在迭代20次时就出现局部最优值，得到最佳的配准结果，配准精度结果为10-17，在精度数量级上超过LM算法和SVD算法。从时间上看，本文方法在配准时间仍然最少的，SVD算法次之，LM算法最多。本文方法在配准精度和速度都好于其他两种算法。

2.2.4 单片点云配准结果

在以上试验中，分别比较了3种算法对完整点云数据的配准结果。为了验证本文方法的普遍有效性，对单片非闭合的点云进行配准。数据采用了Bunny的头部,点云数据量为23 317; Happy的底座,点云数据量为6 823; Dragon的右部分,点云数据量为12 414。分别采用3种算法对以上点云数据进行处理，各自迭代30次，单片点云配准结果如图5所示。

图5 单片点云配准结果

由图5可知，第1行中Bunny的头部，3种算法配准精度无明显的差别；第2行中Happy的底座，LM算法和本文方法明显优于SVD算法；第3行中Dragon的右部分腿，LM算法比本文方法和SVD算法差。为了更加精确、直观地描述3种算法的配准精度和速度，将3种算法各自迭代30次，结果如表4所示。

表4 单片点云配准精度和时间对比

由表4可知，在第1行Bunny中，LM算法在配准精度上要高于SVD算法，但时间上要远大于SVD算法，本文方法在配准精度和时间上都要优于其他两种算法；在第2行Happy中，SVD算法在配准精度和时间上都好于LM算法，本文方法是三者算法中最好的；在第3行Dragon中，LM算法在配准精度上高于SVD算法，本文方法远超LM算法和SVD算法，还是三者中最好的。从总体上来看，本文方法对单片非闭合的点云配准精度最高，精度数量级达到10-17～10-16，与闭合的点云数据几乎一致，其他2种算法在单片非闭合点云的配准上误差较大，与闭合的点云数据相差较大。

3 结束语

点云配准是点云数据处理中最重要的一步，其关键在于求解位置变换矩阵。针对目前求解变换矩阵精度不高、耗时大的问题，提出一种新的求解变换矩阵的方法；结合K-D tree来加快最近点的搜索速度，并采用RANSAC剔除错误的点云，以减少迭代的次数，最终完成点云的配准。试验结果表明，本文方法在配准精度和时间上优于LM算法和SVD算法。本文方法的精度数量级达到10-17～10-16,是其他两种算法不可达到的，由此证明了本文方法的有效性和时效性。下一步将对点云数据有噪声和点云密集程度大的情况开展研究工作。